横向各向同性(TI,Transversely Isotropic)介质属于各向异性介质中对称性最高的六方对称系(Hexagonal Symmetry),拥有一个旋转主对称轴和无数个对称面[1, 2].完全描述TI介质的弹性性质需要5个独立的弹性常数,即C11、C13、C33、C55和C66.与低对称系介质相比,TI介质的独立弹性常数较少,理论公式相对简单,加上TI介质在实际地学问题中很常见,许多岩石和矿物本身就具有内在TI各向异性[3~7],周期性薄互层和定向排列的晶体、裂隙或孔隙也会诱发长波长等效TI各向异性[8~11],考虑TI各向异性对改善成像质量、鉴别岩性、推断裂隙或孔隙优势方向和孔隙度等有重要价值,因此,关于TI介质的理论、实验和数值研究在过去的二十几年里蓬勃发展,基于TI各向异性假设的资料处理解释已经成为一种常规手段[12].
无论是理论和数值研究,还是实际资料反演,都涉及到各向异性参数具体数值的选取.需要注意,各向异性参数的选取并不是任意的,而是必须有物理意义且符合实际介质情况的.基于不恰当的各向异性参数得出的结果是缺乏事实根据的,甚至是错误的.然而,这个问题并没有引起足够的重视,导致在一些文献中出现了不恰当的研究结果.例如,文献[13]在图 1.1中研究了不同各向异性参数[3]条件下的P波波前形状,其中Thomsen参数ε 和δ 的取值范围为-0.6到1.0,而实际上这两个参数必须大于-0.5[14].低于-0.5的ε 意味着弹性常数C11 小于零,沿x1 轴方向的P波速度为虚数;低于-0.5的δ意味着弹性常数C13 为复数,导致某些方向体波速度为复数.这两种情况对完全弹性的各向异性介质来说都是不可能的,具有实际物理意义的弹性常数矩阵,所有分量必须是实数,且所有对角项非负[1, 2].另一个例子是文献[15]中图 2采用的各向异性参数(α0 =4km/s, β0 =2.9km/s, ε= -0.49,δ=-0.24,ρ=3.05g/cm3),如果将这些参数转换成弹性常数,那么各分量分别为C11=0.98GPa, C13=-25.7±2.5iGPa, C33 =48.8 GPa, C55 =25.7GPa, 其中C13为复数.基于这一组错误的各向异性参数,文献[15]的图 2b中出现了随相角单调下降的SV 波相速度和群速度曲线.而事实上,除了在椭圆各向异性情况下SV 波速度与方向无关外[3],其他情况下的SV 波相速度和群速度曲线都不可能单调.SV 波相速度曲线应该是先下降后上升,或者先上升后下降[16],群速度曲线的变化更加复杂.因此,文献[15]中对SV 波相速度和群速度单调性的讨论有误.由此可见,了解TI介质各向异性参数的正确取值范围是非常有必要的.一组简单实用的各向异性参数约束条件对实验室超声测量和野外地震观测数据的各向异性反演也非常有用,一方面可以避免出现无物理意义的反演结果,另一方面有助于加速反演的搜索过程.
|
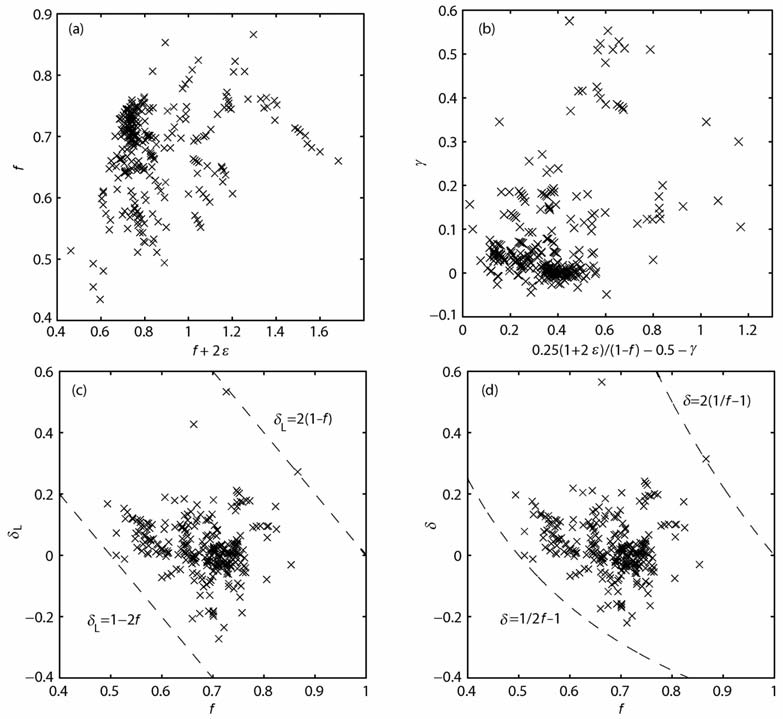
图 1 各向异性参数约束条件检验 (a)ε和f分布;(b) γ分布;(c)δL分布;(d)δ分布. Fig. 1 Maps of laboratorial estimated anisotropic parameters for verification of inequalities (13) proposed in this paper (a) For ε and f;(b) For γ; (c) ForδL ; (d) For δ |
关于TI介质弹性常数和各向异性参数的约束条件,许多文献已经有所涉及.例如,Auld[1] 和Musgrave[2]根据介质的稳定性条件推导了弹性常数的限制条件;Backus[8]、Berryman[9]、Schoenberg[10]、Berryman等[11]讨论了薄互层等效TI介质弹性常数的取值范围;Schoenberg 和de Hoop[17]在推导TI介质慢度分量解析表达式时假设max(C55,C66)< min(C11,C33);Vavrycuk[18]、Thomsen和Dellinger[19]在讨论SV 波波前三叉现象时假设C55<C11,C55<C33,C13+C55>0;李磊[14]在讨论Thomsen 线性近似公式的适用范围时指出,有物理意义的各向异性参数ε和δ 必须大于-0.5.以上结果只是在讨论其它问题时顺带提及,而不是专门的、全面的研究.对TI介质各向异性参数约束条件研究得较为系统的是文献[15]和[20],但是前者根据P 波和SV 波的相速度大于零推导出的29组复杂的限制条件(见其附录)不仅形式复杂不便使用,而且错误较多;后者是对过去文献中相关结果的简单总结,给出的限制条件较为宽泛.本文的目的是提出一套形式紧凑、范围适当的TI介质各向异性参数约束条件,能方便应用于理论研究、数值模拟和实际资料正反演.在下面的小节中,本文首先根据介质稳定性条件对弹性常数的物理约束,以及理论研究和实际观测对弹性常数的经验约束,推导出一组关于各向异性参数的不等式,然后利用实测参数对本文提出的不等式组进行验证,最后,针对一些特殊的TI各向异性和特殊现象,给出了相应的各向异性参数约束条件.
2 对弹性常数的物理约束能量守恒定律是最基本的物理学定律之一,介质的稳定存在和状态变化都必须符合能量守恒定律.取介质的零应变状态为参考,假设介质在外力作用下发生应变,那么无论应变多么微小,能量守恒定律要求其应变势能大于零,这是介质能够稳定存在的充要条件[1, 2].对TI介质,这一稳定性条件等价于要求弹性常数矩阵
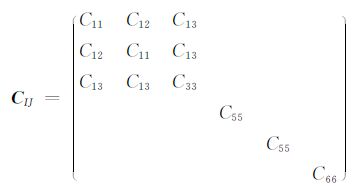
|
(1) |
为正定矩阵(其中C12=C11-2C66).CIJ为正定矩阵的充要条件是所有顺序主子式都大于零,由此可得[1, 2]
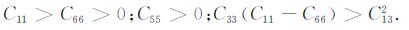
|
(3) |
下面我们将证明,上述不等式足以保证P 波和SV波的相速度在任意方向都大于零.
TI介质中P 波和SV 波的相速度精确表达式为[1~3, 12]
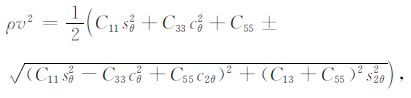
|
(3) |
式中ρ 为密度,v为相速度,θ 为相角,sθ 表示sinθ,c2θ 表示cos2θ(依此类推).根号前正号对应P波,负号对应SV 波,可见SV 波相速度不会高于P 波相速度.
要证明P波和SV 波的相速度大于零,只需证明它们所有的极值点大于零.在相速度极值点处,式(3)对θ 的导数为零,由此可得:
当
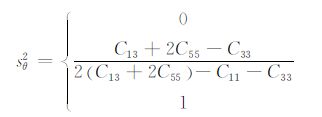
|
(4) |
时,P波相速度极值为
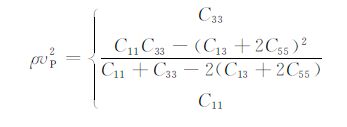
|
(5) |
当
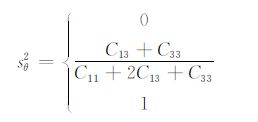
|
(6) |
时,SV 波相速度极值为
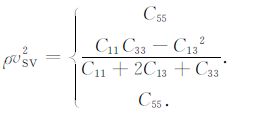
|
(7) |
由于SV 波相速度不会高于P 波相速度,因此只需要证明SV 波的相速度极值大于零.由不等式(2)可知
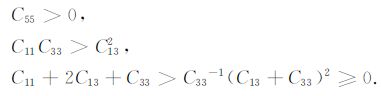
|
(8) |
上式中第三个不等式的推导利用了第二个不等式.由式(8)可知式(7)中SV 波相速度平方的所有极值(包括极小值)都大于零,因此任何方向的SV 波相速度都必定大于零.由此可见,不等式(2)足以保证P波和SV 波的相速度大于零.文献[15]根据SV 波相速度大于零来推导各向异性参数的约束条件,最终给出了29组复杂的不等式作为各向异性参数的约束条件,不仅形式过于复杂,不利于使用,而且有些条件式与不等式(2)相悖,这样的介质违背物质稳定性条件,无法稳定存在.
3 对弹性常数的经验约束理论上,只要TI介质的弹性常数满足不等式(2),那么该介质的存在就是可能的.但是,实际介质(尤其是地学介质)弹性常数的取值范围远小于式(2)给定的范围.根据弹性常数各分量的物理意义,本文提出以下经验性约束条件:
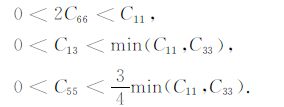
|
(9) |
在下面的段落中我们将逐个讨论式(9)中各不等式的依据和意义.
注意C12= C11 -2C66,因此第一个不等式中2C66 <C11 等价于C12>0.这里解释C12和C13 大于零的依据和意义:假设TI介质在外力作用下沿主对称轴(x3 轴)发生单轴应变,即除沿x3 轴的正应变e3 外,其余应变分量都为0,由胡克定律可知,沿x1 轴的正应力σ1 =C13e3,由此可见,C13 表示的物理意义是介质在沿x1 轴的正应力作用下抵抗沿x3轴方向发生正应变的能力(或者在沿x3 轴的正应力作用下抵抗沿x1 轴方向发生正应变的能力;C12的物理意义与此类似).如果C13 小于0,那就意味着在沿x1 轴的拉伸(压缩)作用下,介质在x3 轴方向将发生膨胀(收缩),此时的泊松比为负数.负泊松比理论上是可以存在的,各向同性介质泊松比的理论值就在-1~0.5之间[21],而且具有负泊松比的人造材料也已成功合成[22],在各向异性介质的非对称轴方向出现负泊松比的现象也很普遍[23].但是,对自然形成的介质(尤其是岩石),在对称轴方向出现负泊松比的情况很难出现.我们查找了大量有关金属、单晶矿物、岩石和聚合物弹性常数的文献和数据手册[1~5, 7, 24~26],在六方对称系中几乎没有C12或C13为负数的介质,少数几个例外情况也极有可能是测量或反演误差引起的,例如Gold[27]在室温下测量金属铍的弹性常数为C11=308GPa, C12=-58GPa, C13=8.7GPa, C33=357GPa, C55=110 GP,其中C12为负数,但数值上远小于C11 和C33 .后来的研究[28~30]表明,室温下铍的C12应该在14.8~26.8GPa之间,文献[27]中出现负的C12是因为计算弹性常数所用的近似公式是基于弱各向异性假设,不适用于铍这类强各向异性介质.因此,我们认为假设TI介质的C12和C13 大于零是安全的、合理的.
由式(8)中C11C33 > C132 可知C11 +C33 =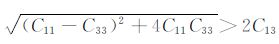
式(9)中的最后一个不等式主要是为了限制对称轴方向的S 波速度,使其大于零且低于P 波速度,式中的系数3/4使得S 波速度不至于过于接近P波速度,该系数等价于假设沿对称轴方向的P/SV波速度比大于1.15(实测的P/SV 波速度比通常在1.4以上).我们检查了一些文献和数据手册[1~5, 7, 24~26]中TI介质各弹性常数的相对大小,发现C11 与C33之间、C55 与C66 之间不存在必然的大小关系,但都满足该不等式.对各向同性介质,不等式(9)恒成立.
4 对各向异性参数的约束用弹性常数表示的解析公式通常形式复杂,不利于简化,且物理意义不够直观,因此,在实际应用中通常采用1986年Thomsen定义的TI介质各向异性参数[3].Thomsen参数是弹性常数的简单代数组合,但将各向异性的效应从各向同性背景中剥离出来,便于简化公式,且能更直观地体现各向异性的特征.Thomsen参数的提出很大程度上推动了各向异性在理论研究和实际应用方面的发展.Thomsen参数的定义为[3]
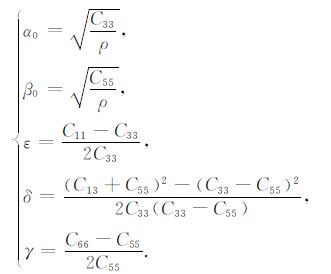
|
(10) |
ε约等于平行和垂直于对称轴方向的P 波速度的相对差别,其大小反映P波各向异性的强弱;δ 控制P波在小角度的各向异性,与NMO 速度直接相关,与岩性关系密切,是最重要的Thomsen 参数;γ 约等于平行和垂直于对称轴方向的SH 波速度的相对差别,其大小反映SH 波各向异性的强弱[3, 12].参数δ还有一种线性的定义方式δL = (C13+2C55-C33)/C33,两者之间的关系为
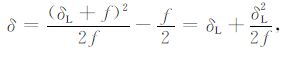
|
(11) |
式中:
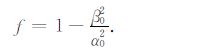
|
(12) |
由式(11)可以看出,δ ≥δL,但两者必定同号,且差别为二阶小量,通常可以忽略.
利用公式(10)~ (12),将关于TI介质弹性常数的限制条件转化为关于各向异性参数的限制条件,得:
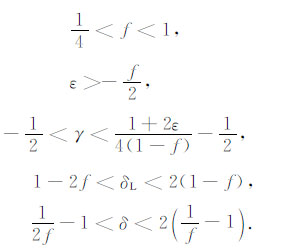
|
(13) |
具体过程参见本文附录.从上式可以看出:ε、δ、γ 的取值区间主要受到P 波和S波的参考速度比α0/β0的约束,其中γ 的取值上限还受ε 的限制;波速比α0/β0 以及各向异性参数δ 和γ 的取值都有上、下限,而ε的取值没有上限.我们对281组实测各向异性参数[3, 5]进行了检验,都满足上述约束条件(见图 1).从图 1a可以看出,实测f值都在0.4以上,明显高于不等式(13)给出的下限1/4,再次说明式(9)中系数3/4是安全的;实测f+2ε值都在0.5以上,明显高于不等式(13)给出的下限0,说明岩石和矿物的各向异性参数ε 较少出现大的负值.我们找到的f+2ε值最低的是霞石[4],其f=0.7,ε =-0.18,f+2ε=0.33.目前岩石物理超声测量已经发现了许多正ε极大的情况,例如页岩[3, 5~7]的ε 可达0.5以上,风化石膏和云母晶体矿物[3]的ε 在1.12~1.22之间,干燥Angers板岩的ε更是超过1.5.我们找到的最极端的例子是石墨[4],其ε 高达14.02.从图 1b可以看出,γ 的特点与ε 比较类似,实测γ 值都在-0.1以上,明显高于不等式(13)给出的下限-1/2,说明γ 较少出现大的负值.与ε 不同的是,γ的取值存在理论上限,并存在与不等式(13)给出的上限非常接近的情况(即图 1b中横坐标接近0的情况).从图 1(c~d)可以看出,实测δ 和δL 的值都在限定范围内(图中虚线),而且存在非常接近上下限的情况,说明不等式(13)给出的范围不仅合理,而且恰到好处.
需要注意,不等式(13)与不等式(2)和(9)并不完全等价,而是以简洁性为主要原则来选择上、下限的结果.实际上,ε和γ 与δ 和δL 之间也存在一定的约束关系.例如,严格的δL 上限可表示为2[1-f+min(0,ε)],但因为负ε较少且远小于1-f,所以这种约束力不强.从图 2(a, b)中也可以看出ε与δ(δL)之间没有明显的相关性,同样,从图 2d中可以看出γ 与δ 之间没有明显的相关性.但是,从图 2c可以看出,ε与γ 之间存在明显的正相关.

|
图 2 实测各向异性参数分布图 (a)εδL分布;(b)εδ分布;(c)εγ分布;(d)γδ分布. Fig. 2 Maps of laboratorial estimated anisotropic parameters for investigation of correlations between parameters |
从图 1,2还能看出,ε、δ 和γ 都可正可负,但ε和γ 正值较多,负值较少,而δ 正负值出现的频率相当.负δ对应较小的C13(C13 <C33-2C55),正的δ对应较大的C13(C13 >C33 -2C55).对大多数情况,ε在-0.05~0.45之间,δ 在-0.2~0.3 之间,γ 在-0.05~0.2之间.但是需要注意,不同岩石和矿物的各向异性参数差异较大,同种岩石和矿物在不同温压状态下各向异性参数也会发生变化,以上数值范围只是针对有限的几种岩石的统计结果,不一定具有普适性.其他作者也提出过一些各向异性参数的数字参考范围.例如,Backus[8]认为,常见的P/S波速比范围在1.52~2.22之间;Berge[20]认为固结的沉积岩波速比范围在1.5~2之间,未固结的沉积岩波速比更大;Tsvankin[12]提出,在实际勘探中感兴趣的波速比范围在1.5~2.5之间,ε 在-0.05~0.45之间,δ在-0.2~0.3之间;Fowler[31]推荐的波速比范围在$\sqrt{2}$~4之间,ε在0~0.2之间,δ 在0.05~0.1之间.需要强调,不论是岩石物理超声实验还是野外地震勘探,都已经发现许多在这些数值范围之外的测量结果,因此,在使用这些数值范围时,一定要事先确定这些范围是否适用于研究对象.
5 特殊情况椭圆各向异性介质是一种特殊的TI介质,在各向异性研究的发展史中起过重要作用[32, 33];周期性薄互层引起的长波长等效各向异性是实际生产中很常见、很重要的一种TI各向异性.因此,在本节中我们专门讨论了这两种特殊各向异性的Thomsen参数取值范围.此外,TI介质中有一些特别的、可观测到的物理现象,出现这些现象需要各向异性参数满足特殊的约束条件,我们对这些约束条件也作了总结.
5.1 椭圆各向异性椭圆各向异性介质是TI介质中极其特殊的一种,椭圆各向异性介质中P波的波前为旋转椭球面,SV 波的波前为球面(即SV 波为各向同性).椭圆各向异性的解析公式远比一般TI的解析公式要简单.在20世纪90年代之前,椭圆各向异性假设曾经被大量采用.如今,椭圆各向异性在实际资料反演中仍可以作为初步建立各向异性介质模型的工具.此外,在天然地震学中,常常只用一个参考速度和一个各向异性强度百分比来描述介质的各向异性,这种假设实际上等价于椭圆各向异性假设.出现椭圆各向异性的充要条件[3, 32, 33]是ε=δ,利用该等式将式(9)中关于ε和δ 的不等式合并,得
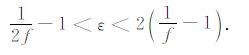
|
(14) |
周期性薄互层是一种常见的地学介质,在长波长条件下会表现出与均匀TI介质相同的性质,被称为等效TI各向异性[8~11].对各向同性薄互层诱发的TI各向异性,理论研究[8~11]已经证明,0 <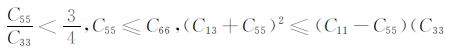
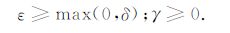
|
(15) |
各向异性介质中的径向方向[34](longitudinaldirections)就是P 波相速度为极值的方向,在这些方向P波相速度对相角的导数为零,相速度与群速度相等,P波的相传播方向、群传播方向与偏振方向重合,并都与S波的偏振方向垂直,这些现象非常类似于各向同性介质中波的传播特征,不同之处在于SV 波和SH 波依然分裂.基于以上特征,径向方向在实验室和野外观测中都有可能被观测到,并可以用来确定介质的对称系[34].式(4)给出了TI介质中径向方向的解析公式,其中相角为0°和90°的方向必然是径向方向,而中间角度的径向方向是否出现取决于各向异性参数之间的关系.如果中间角度出现径向方向,那么式(4)中sθ2 必须介于0和1之间.利用式(4)和(10),可知中间角度出现径向方向的充要条件为
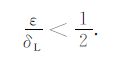
|
(16) |
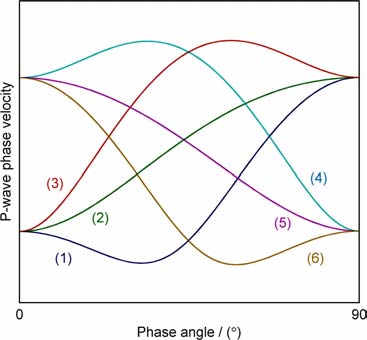
更详细的中间角度出现径向方向的各类情况如图 3所示.如果观测到径向方向,可以依据图 3给出的约束条件来判断各向异性参数之间的相互关系,甚至可以利用式(4)和(5)直接反演弹性常数和各向异性参数.
|
图 3 不同形态的TI介质P波相速度曲线 出现此类曲线的条件按编号依次为:(1)ε>0,δL<0;(2)ε>0,0≤δL≤2ε;(3)ε≥0,δL>2;(4)ε<0,δL>δL>0;(5)italic>ε<0,2ε≤δL≤0;(6)ε≤0,δL<2ε. Fig. 3 Patterns of P-wave phase velocity curve in a TI medium |
TI介质中SH 波的波前为椭球面,P 波的波前为类椭球面,而SV 波的波前较为复杂,除了常规的类椭球面以外,还有可能出现自我交叉[1, 2, 18, 19, 35, 36].SV 波波前出现三叉现象的充要条件是SV 波的慢度面出现凹陷[2, 17~19, 35],在波前出现三叉现象的方向,SV 波走时出现多值性,能量发生会聚,这些现象可以在实际资料中观测到[37],并且会使横波和转换波的数据处理变得更加困难[36],但在另一方面,波前三叉现象也能为各向异性参数反演提供约束信息.研究表明[35],在x1 轴方向出现三叉现象(基向三叉;basaltriplication)的条件为(C13 +C55)2 -C33(C11 -C55)>0;在x3 轴方向出现三叉现象(轴向三叉;axialtriplication)的条件为(C13 +C55)2 -C11(C33-C55)>0;如果同时满足前两个条件,那么在x1 轴和x3 轴都会出现三叉现象(双重三叉;doubletriplications);在倾斜方向出现三叉现象(倾向三叉;obliquetriplication)的条件为(C13 +C55)2 -3C552 +C55(C11+C33)-3C11C33+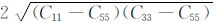
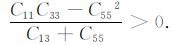
|
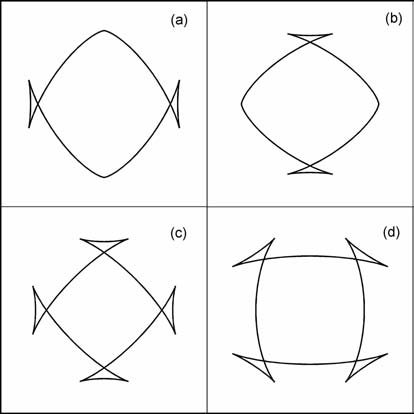
图 4 四种SV波波前三叉现象 (a)基向三叉;(b)轴向三叉;(c)双重三叉;(d)倾向三叉. Fig. 4 Illustrations of SV wavefront triplications (a) Basal triplication; (b) Axial triplication; (c) Double triplications; (d) Oblique triplication. |
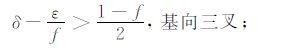
|
(17) |
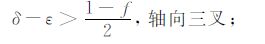
|
(18) |
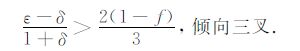
|
(19) |
其中式(19)是简化后的近似公式.从式(17)~(19)可以看出:当式(17)和(18)同时成立时,沿x1 轴和x3 轴方向的波前三叉可以同时出现(即双重三叉),但倾斜方向的波前三叉只能单独出现;椭圆各向异性介质ε=δ,不会出现波前三叉现象;当介质偏离椭圆各向异性时(即ε 与δ 的差别增大),波前三叉现象开始出现;基向和轴向三叉在ε 变小、δ 变大(C13 变大)时变得明显,倾向三叉在ε 变大、δ 变小(C13变小)时变得明显;结合式(15)可知各向同性薄互层等效TI介质中可能出现倾向三叉,但不会出现基向和轴向三叉,实际上对其他地学TI介质也比较容易符合倾向三叉出现的条件,而难以满足出现基向和轴向三叉的条件,尤其是难以只满足其中之一,正因为如此,在野外观测中三叉现象通常只在长炮检距时出现[19].此外,Vavrycuk[18]指出,波前三叉现象不会在各向异性强度低于8.86% ~9.72%的弱TI介质中出现,但也不能保证在强TI介质中一定出现.
6 向斜方介质的扩展斜方(也称正交各向异性)介质属于正交对称系,有9个独立的弹性常数,其弹性常数矩阵的形式为
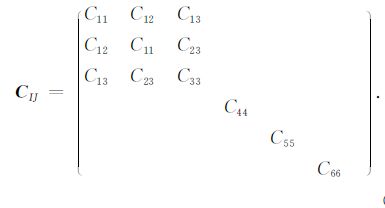
|
(20) |
斜方介质弹性常数矩阵的非零项与TI介质相同,但各分量之间不存在等式关系.在地学问题中,常见的斜方介质是在VTI背景中嵌入定向排列的直立裂隙形成的等效斜方介质[38],文献[7]中的气煤就是一种典型的例子.尽管文献[7]中作者将气煤近似作为TI介质来看待,但从文中的描述来看,由于节理的存在煤岩本身就具有强TI介质的性质,再加上气煤中垂直于煤层面的裂隙非常发育,因此将气煤视为斜方介质更为恰当.从文献[7]表 2中给出的不同方向体波速度的差异也能看出气煤具有正交各向异性.除了由结构引起的等效正交各向异性外,很多矿物本身也具有内在正交各向异性[1, 2, 4, 25, 26].目前关于斜方介质中地震波传播的理论和数值研究[12, 38~42]已经有了一定的发展,但实验室岩样超声测量[43]的结果还比较少,斜方介质在实际生产中的应用也很罕见.到目前为止,我们还没有发现关于斜方介质各向异性参数取值范围的研究结果发表.在本节中,我们试图将上文中对TI介质弹性常数和各向异性参数的讨论推广到斜方介质.
6.1 物理约束与上文中关于TI介质的讨论类似,物质稳定性条件同样要求斜方介质的弹性常数矩阵为正定矩阵,式(14)的所有顺序主子式都必须大于零,由此可得:
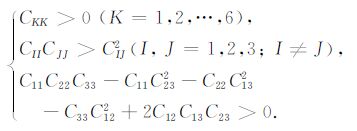
|
(21) |
(21) 式不对重复下标求和.
6.2 经验约束考虑到物质稳定性条件和弹性常数的物理意义,一般来说,上文中关于TI介质弹性常数的讨论对低对称系的斜方介质也成立.我们将式(9)推广到斜方介质,提出以下经验性约束条件:
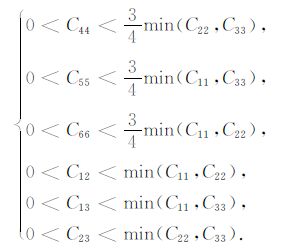
|
(22) |
根据Voigt规则(下角标11→1,22→2,33→3,23→4,13→5,12→6),上式可以简写成
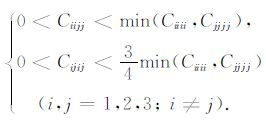
|
(23) |
在将式(9)推广到斜方介质的过程中,需要注意保持弹性常数下标的轮换对称性,如果不考虑这种对称性,可能会错误地得到如下结果
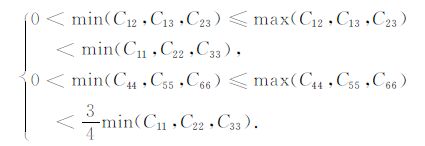
|
(24) |
这里保持弹性常数下标的轮换对称性实质上相当于在每个独立的对称面内考察弹性常数之间的关系.众所周知,斜方介质对称面内的弹性波性质与TI介质非常类似[2],而对实际介质而言,不同对称面内的弹性常数不一定存在制约关系,因此式(24)并不一定成立.在实际介质中也确实有一些不符合式(24)的例子,例如橡木[2]的弹性常数为:C11 =0.305GPa, C12=0.103 GPa, C13 =0.150 GPa, C22=0.138GPa, C23=0.103GPa, C33=0.682GPa, C44=0.78GPa, C55=0.132GPa, C66=0.40GPa, 其中C13小于同一对称面内的C11 和C33,但是大于与之垂直对称面内的C22,因此不满足式(24).
我们检查了现有的文献和工具书中[1, 2, 4, 25, 26]斜方介质的弹性常数,绝大多数都符合式(22)、(23),只有极个别单晶矿物例外,例如甲酸锶[24]晶体的弹性常数为:C11 =43.9 GPa, C12=10.4 GPa, C13 =-14.9GPa, C22 =34.8 GPa, C23 = -1.4 GPa, C33=37.4GPa, C44 =15.4 GPa, C55 =10.7 GPa, C66=17.2 GPa, 其中C13 和C23 为负数;四方晶系(可视为正交对称系的特殊情况)中的磷酸二氢铵晶体[25]的弹性常数为:C11 =67.47 GPa, C12=-10.66GPa, C13 =16.52GPa, C33 =30.22GPa, C55 =6.85GPa, C66 =6.39GPa, 其中C12为负数;四方晶系中的二氧化碲晶体[1]的弹性常数为:C11=55.7GPa, C12=51.2GPa, C13 =21.8GPa, C33 =105.8GPa, C55 =26.5GPa, C66 =65.9GPa, 其中C66 大于C11 .但是,这些例外的弹性常数数据来自于物理学的文献而不是地学文献,测量弹性常数的温度、压力环境有差异,而且也不能排除这些例外情况是由于测量误差或反演过程中使用近似公式引起的可能性.再者,地学介质多为复合物而非单晶,地学问题中观测到的各向异性通常是由晶格优势方向、形状优势方向等结构因素引起的地震波长波长等效各向异性,而非晶体本身的各向异性.在复合物中没有发现不符合式(22)、(23)的情况.
6.3 对各向异性参数的约束Tsvankin[38]在1997 年将Thomsen 定义的TI介质各向异性参数推广到斜方介质,提出以下各向异性参数:

|
(25) |
其中参数δ 也有线性的定义方式:
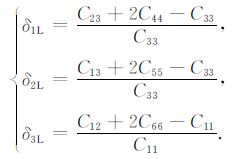
|
(26) |
两者之间存在的关系为:
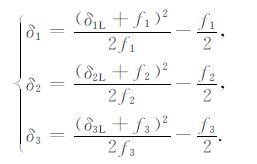
|
(27) |
其中

|
(28) |
将弹性常数约束条件转换成各向异性参数的约束条件,得
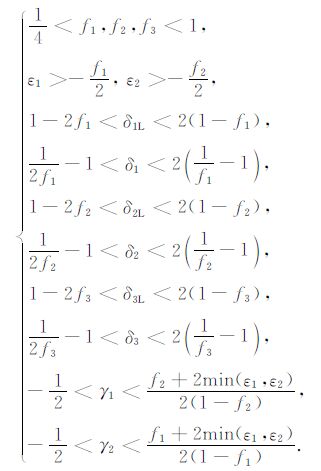
|
(29) |
由式(29)可见,在对称面内斜方介质弹性常数之间的制约关系与TI介质类似,但是不同对称面内的关系有差别(参数下标不同).目前关于斜方介质的实测数据较少,不足以如同上文中TI介质一样利用大量实测参数来检验上述不等式和研究各参数之间的相关性.除此以外,还有一个问题就是目前的文献中关于斜方介质各向异性参数的定义并不统一,其中ε1、ε2、δ1、δ2 这四个参数的定义比较一致,但是δ3、γ1、γ2 这几个参数的定义有差异,例如文献[44, 45]中的定义为
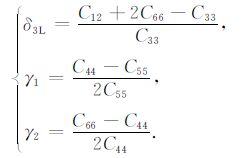
|
本文根据介质稳定性条件、弹性常数物理意义和各向异性波动理论,结合实测各向异性参数,提出了一组简洁的TI介质各向异性参数约束条件.举例分析了现有研究中存在的一些由于忽视各向异性参数约束条件而导致的不合理研究结果,强调了在研究和实践中重视各向异性约束条件的必要性.此外,还专门给出了椭圆各向异性介质和薄互层等效TI介质的附加约束条件,以及出现某些特殊偏振方向或三叉现象所对应的参数条件.此外,本文还给出了斜方介质的物质稳定性条件,并将TI介质弹性常数和各向异性参数的约束条件推广到斜方介质.本文提出的约束条件的最大特点是简单易用,且范围恰当,可为理论研究和数值模拟中各向异性参数的取值提供依据,为实验室测量和野外观测数据的各向异性参数反演提供约束.
附 录
本附录给出由弹性常数的约束关系式(9)推导各向异性参数的约束关系式(13)的过程.如文中所述,式(13)与式(9)并不完全等价,而是考虑了简洁性的结果,因此式(13)的范围实际上略大于式(9).
由各向异性参数的定义式(10)可得如下等式:
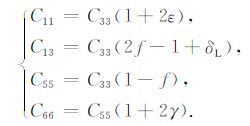
|
下面的推导主要是利用了这几个等式,将这些等式代入关于弹性常数的不等式后化简,即得关于各向异性参数的不等式.
由0<C55 <34C33 ,得14<f<1.
由C11 >C55 ,得ε>$-\frac{f}{2}$.
由C13 >0,得δL >1-2f;由C13 <C11,得δL <2(1-f+ε);由C13 <C33,得δL <2(1-f).如文中所述,ε和δL 之间无明显相关性,因此我们取1-2f<δL <2(1-f).再由式(11)给出的δ与δL 之间的关系,得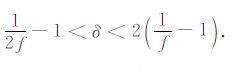
由C66 >0,得γ >-$\frac{1}{2}$;由C11 >2C66,得γ 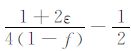
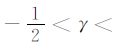
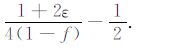
将斜方介质弹性常数约束转换成各向异性参数约束的过程与此类似,主要是利用以下等式进行替换,具体过程这里不再赘述.
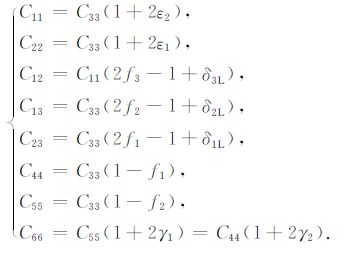
|
| [1] | Auld B A. Acoustic Fields and Waves in Solids, 2nd ed. Malabar: Krieger , 1990. |
| [2] | Musgrave M J P. Crystal Acoustics. San Francisco: Holden-Day , 1970. |
| [3] | Thomsen L. Weak elastic anisotropy. Geophysics , 1986, 51(10): 1954-1966. DOI:10.1190/1.1442051 |
| [4] | Ahrens T J. Mineral Physics & Crystallography. In: A Handbook of Physical Constants. Washington: American Geophysical Union Washington, 1995 |
| [5] | Wang Z J. Seismic anisotropy in sedimentary rocks, part 2: Laboratory data. Geophysics , 2002, 67(5): 1423-1440. DOI:10.1190/1.1512743 |
| [6] | 邓继新, 史鱒, 刘瑞繤, 等. 泥岩、页岩声速各向异性及其影响因素分析. 地球物理学报 , 2004, 47(5): 862–868. Deng J X, Shi G, Liu R X, et al. Analysis of the velocity anisotropy and its affection factors in shale and mudstone. Chinese J. Geophys. (in Chinese) (in Chinese) , 2004, 47(5): 862-868. |
| [7] | 董守华. 气煤弹性各向异性系数实验测试. 地球物理学报 , 2008, 51(3): 947–952. Dong S H. Test on elastic anisotropic coefficients of gas coal. Chinese J. Geophys. (in Chinese) (in Chinese) , 2008, 51(3): 947-952. |
| [8] | Backus G E. Long-wave elastic anisotropy produced by horizontal layering. J. Geophy. Res. , 1962, 67(11): 4427-4440. DOI:10.1029/JZ067i011p04427 |
| [9] | Berryman J G. Long-wave elastic anisotropy in transversely isotropic media. Geophysics , 1979, 44(5): 896-917. DOI:10.1190/1.1440984 |
| [10] | Schoenberg M. Transversely isotropic media equivalent to thin isotropic layers. Geophysical Prospecting , 1994, 42(8): 885-915. DOI:10.1111/gpr.1994.42.issue-8 |
| [11] | Berryman J G, Grechka V Y, Berge P A. Analysis of Thomsen parameters for finely layered VTI media. Geophysical Prospecting , 1999, 47(6): 959-978. DOI:10.1046/j.1365-2478.1999.00163.x |
| [12] | Tsvankin I. Seismic Signatures and Analysis of Reflection Data in Anisotropic Media. New York: Pergamon Press, 2001 . |
| [13] | Xiao C Y. A comparison of different methods for estimating Thomsen's anisotropy parameters. Calgary: Department of Geology and Geophysics, University of Calgary , 2006. |
| [14] | 李磊. 横向各向同性介质Thomsen近似公式的适用范围. 石油物探 , 2008, 47(2): 116–122. Li L. Applicability of Thomsen approximate formula in transversely isotropic media. Geophysical Prospecting for Petroleum (in Chinese) (in Chinese) , 2008, 47(2): 116-122. |
| [15] | 马德堂, 朱光明. 关于横向各向同性介质中的Thomsen参数取值的讨论. 石油地球物理勘探 , 2006, 41(4): 431–438. Ma D T, Zhu G M. Discussion on taking values of Thomsen parameters in transverse isotropic media. Oil Geophysical Prospecting (in Chinese) (in Chinese) , 2006, 41(4): 431-438. |
| [16] | 李磊. TI介质中的相速度和群速度及射线参数. 石油物探 , 2008, 47(4): 334–337. Li L. Phase velocity, group velocity, and ray parameters in transversely isotropic media. Geophysical Prospecting for Petroleum (in Chinese) (in Chinese) , 2008, 47(4): 334-337. |
| [17] | Schoenberg M A, de Hoop M V. Approximate dispersion relations for qP-qSV-waves in transversely isotropic media. Geophysics , 2000, 65(3): 919-933. DOI:10.1190/1.1444788 |
| [18] | Vavrycuk V. Generation of triplications in transversely isotropic media. Physical Review B , 2003, 68(5): 54107. DOI:10.1103/PhysRevB.68.054107 |
| [19] | Thomsen L, Dellinger J. On shear-wave triplication in transversely isotropic media. Journal of Applied Geophysics , 2003, 54(3-4): 289-296. DOI:10.1016/j.jappgeo.2003.08.008 |
| [20] | Berge P A. Constraints on elastic parameters and implications for lithology in VTI media. SEG Technical Program Expanded Abstracts , 1995, 14(1): 906-909. |
| [21] | Aki K, Richards P G. Quantitative Seismology, Theory and Methods. Freeman , 1980. |
| [22] | Lakes R. Foam structures with a negative Poisson's ratio. Science , 1987, 235(4792): 1038-1040. DOI:10.1126/science.235.4792.1038 |
| [23] | Baughman R H, Shacklette J M, Zakhidov A A, et al. Negative Poisson's ratios as a common feature of cubic metals. Nature , 1998, 392(6674): 362-365. DOI:10.1038/32842 |
| [24] | Hearmon R F S. The elastic constants of anisotropic materials - II. Advances in Physics , 1956, 5(19): 323-382. DOI:10.1080/00018732.1956.tADP0323 |
| [25] | Simmons G, Wang H. Single Crystal Elastic Constants and Calculated Aggregate Properties: A Handbook, 2nd ed. Cambridge: M. I. T. Press, 1971 . |
| [26] | Madelung O, Martienssen W. Landolt-Brnstein: Numerical Data and Functional Relationships in Science and Technology-New Series, Annual volumes 11996. Springer-Verlag , 1996. |
| [27] | Gold L. Evaluation of the stiffness coefficients for beryllium from ultrasonic measurements in polycrystalline and single crystal specimens. Physical Review , 1950, 77(3): 390-395. DOI:10.1103/PhysRev.77.390 |
| [28] | Smith J F, Arbogast C L. Elastic constants of single crystal Beryllium. Journal of Applied Physics , 1960, 31(1): 99-102. DOI:10.1063/1.1735427 |
| [29] | Rowlands W D, White J S. The determination of the elastic constants of beryllium in the temperature range 25 to 300℃. Journal of Physics F: Metal Physics , 1972, 2(2): 231-236. DOI:10.1088/0305-4608/2/2/011 |
| [30] | Migliori A, Ledbetter H, Thoma D J, et al. Beryllium's monocrystal and polycrystal elastic constants. Journal of Applied Physics , 2004, 95(5): 2436-2440. DOI:10.1063/1.1644633 |
| [31] | Fowler P. Practical approximations: A systematic anatomy. Presented at the 10th Intenational Workshop on Seismic Anisotropy , 2002. |
| [32] | Byun B S. Seismic parameters for media with elliptical velocity dependencies. Geophysics , 1982, 47(12): 1621-1626. DOI:10.1190/1.1441312 |
| [33] | Helbig K. Elliptical anisotropy-Its significance and meaning. Geophysics , 1983, 48(7): 825-832. DOI:10.1190/1.1441514 |
| [34] | Helbig K. Longitudinal directions in media of arbitrary anisotropy. Geophysics , 1993, 58(5): 680-691. DOI:10.1190/1.1443452 |
| [35] | Payton R G. Elastic Wave Propagation in Transversely Isotropic Media. Netherlands: Martinus Nijhoff Publishers , 1983. |
| [36] | Roganov Y, Stovas A. On shear-wave triplications in a multilayered transeversely isotropic medium with vertical symmetry axis. Geophysical Prospecting , 2010, 58(4): 549-559. |
| [37] | Slater C, Crampin S, Brodov L Y, et al. Observations of anisotropic cusps in transversely isotropic clay. Journal of the Canadian Society of Exploration Geophysicists , 1993, 29(1): 216-226. |
| [38] | Tsvankin I. Anisotropic parameters and P-wave velocity for orthorhombic media. Geophysics , 1997, 62(4): 1292-1309. DOI:10.1190/1.1444231 |
| [39] | Grechka V, Tsvankin I. 3-D moveout velocity analysis and parameter estimation for orthorhombic media. Geophysics , 1999, 64(3): 820-837. DOI:10.1190/1.1444593 |
| [40] | Bakulin A, Grechka V, Tsvankin I. Estimation of fracture parameters from reflection seismic data-Part II: Fractured models with orthorhombic symmetry. Geophysics , 2000, 65(6): 1803-1817. DOI:10.1190/1.1444864 |
| [41] | Grechka V, Pech A, Tsvankin I. Parameter estimation in orthorhombic media using multicomponent wide-azimuth reflection data. Geophysics , 2005, 70(2): D1-D8. DOI:10.1190/1.1897026 |
| [42] | 卢明辉, 唐建侯, 杨慧珠, 等. 正交各向异性介质P波走时分析及Thomsen参数反演. 地球物理学报 , 2005, 48(5): 1167–1171. Lu M H, Tang J H, Yang H Z, et al. P-wave traveltime analysis and Thomsen parameters inversion in orthorhombic media. Chinese J. Geophys. (in Chinese) (in Chinese) , 2005, 48(5): 1167-1171. |
| [43] | 魏建新, 狄帮让, 王椿镛. 岩石正交各向异性的实验观测. 地球物理学进展 , 2008, 23(2): 343–350. Wei J X, Di B R, Wang C Y. The experimental observation of the rock orthorhombic anisotropy. Progress in Geophysics (in Chinese) (in Chinese) , 2008, 23(2): 343-350. |
| [44] | Mensch T, Rasolofosaon P. Elastic-wave velocities in anisotropic media of arbitrary symmetry-generalization of Thomsen's parameters ε, δ and γ. Geophysical Journal International , 1997, 128(1): 43-64. DOI:10.1111/gji.1997.128.issue-1 |
| [45] | Peník I, Gajewski D. Polarization, phase velocity, and NMO velocity of qP-waves in arbitrary weakly anisotropic media. Geophysics , 1998, 63(5): 1754-1766. DOI:10.1190/1.1444470 |
 2011, Vol. 54
2011, Vol. 54

