2. 中国地震台网中心, 北京 100045
2. China Earthquake Networks Center, Beijing 100045, China
直流电机驱动的城市轨道交通开行过程中对地漏电致使地下电性结构改变,产生干扰磁场导致周围数十公里范围内的地磁观测台站的相对观测数据受到污染[1-3],进而影响地磁台站观测数据质量,制约地磁观测工作的开展.
轨道交通对地漏电产生的磁场受到机车开行间隔变化、钢轨漏电不均匀性[4]、地下介质导电率差异[5,6]等因素的影响,时间域上呈现出不规则性,本质上具有非平稳特性的磁场信号的特征.其主要干扰频率段与外源场某些不规则扰动的频率成分重合,传统滤波手段不能同时满足最大程度抑制轨道交通干扰和最大限度保留地磁场信号的要求.
小波技术[7]是研究地磁信号[8]及轨道交通干扰等非平稳信号的有效手段,通过小波变换可在不同尺度、不同时刻表述信号及干扰的时频特征.通过小波变换抑制干扰一般由以下三个步骤完成[9]:第一步小波变换;第二步对小波系数进行非线性处理以滤除干扰;第三步小波逆变换.第二步中小波系数的重要程度的判断、阈值的选取以及阈值施加函数的确定是小波干扰抑制的关键技术.对小波系数进行非线性处理方法包括Mallat 提出的模极大值算法[10],(Xu)等[11]提出的空域相关滤波算法及Donoho[12]提出的阈值滤波算法.
目前使用小波技术对轨道交通进行抑制普遍采用阈值滤波算法.如通用阈值、极小化风险阈值、假设检验法和BayesShrink 阈值等[13,14].但采用这些阈值确定方法的都是基于独立正态分布的白噪声模型,没有分析轨道交通干扰本身在多分辨率下的时频特征.不加区别地使用基于白噪声模型的阈值算法抑制轨道交通的干扰[15-17]会导致抑制结果中高频部分损失太多,及地磁数据中不规则变化的扰动磁场特征并没有合理保留等问题.
本文以天津轨道交通干扰为例,选取中国数字地磁台网中受干扰的天津静海台(地理经度116.86°E,纬度38.94°N;磁经度188.07°E,纬度29.07°N)和相邻未受干扰参考台站河北红山台(地理经度114.70°E,纬度37.39°E;磁经度186.19°E,纬度27.47°N)2009年6-11月共183 天相对观测数据.通过对这两个台站观测数据的分析,得出受干扰台站轨道交通干扰的功率谱特征和干扰在不同细节尺度下小波系数统计特征.在此基础上采用改进的小波域尺度间模型对观测台站晚间未受干扰观测数据进行提取;把受干扰的观测数据分为磁静日和磁扰日两组,采用尺度内模型对各受干扰细节尺度小波系数阈值进行有效估算并进行抑制.在抑制结果分析中,除了采用常规视觉效果和功率谱特征比较外,还引入同纬度第二参考台站喀什栏杆乡台(地理经度76.01°E,纬度39.45°E;磁经度151.57°E,纬度30.86°N),考察了静海台干扰抑制前后时域峰峰值特征并与两座参考台站进行比较;最后采用本方法对两座参考台站观测数据进行抑制,考察了该方法对无轨道交通干扰地磁观测数据的抑制损失大小.
2 方法及干扰分析 2.1 连续小波变换及离散小波变换信号x(t)的连续小波变换定义为

|
(1) |
其中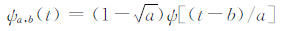
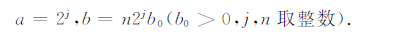
|
用t轴将b0 归一化后,信号x(t)的离散小波变换为
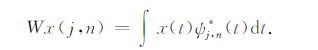
|
(2) |
计算上述离散小波变换的快速算法为Mallat 算法[18].该快速小波分解算法使数据经过树状理想滤波器组得到各尺度上小波系数dj(t),每个尺度所对应的伪频率(pseudo-frequencies)可由式(3)得出

|
(3) |
式中a为以2为底的幂级数离散尺度,Δ 为采样率,Fc 为所采用的小波在不同尺度对应的中心频率,Fa为该尺度所对应的频率.本文采用Daubechies系列的dB8小波[19],尽管没有函数表达式,但它具有双正交、紧支撑、且拥有较高的消失距,非常适合对此类干扰的分析.
2.2 轨道交通干扰的功率谱特征分析天津静海地磁台地磁相对观测数据受轨道交通干扰后,垂直分量(Z)受干扰最大,振幅增大,直观上看曲线变粗.这与轨道交通开行后直流供电系统在钢轨上的漏电电流产生的磁场主要集中在垂直分量(Z),其次为磁偏角分量(D),水平分量(H)受到干扰最小的理论模型相吻合.晚间机车停止运行后干扰消失,凌晨机车开动后干扰出现.
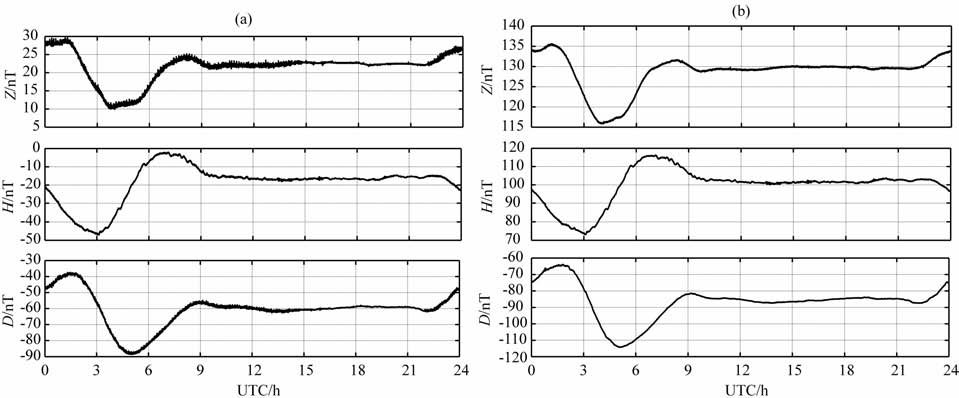
图 1是静海台和红山台2009年10月20日(ΣKp=1-)地磁相对观测水平分量(H)、磁偏角分量(D)及垂直分量(Z)记录数据.从图中可以看出这两个台站三个分量之间有较好的空间相关性.静海台受天津轨道交通的干扰,在垂直分量(Z)能够明显观察到干扰导致曲线变粗,同时磁偏角分量(D)也可观察到少许的干扰.时间上看,大约在UTC0∶00-15∶00 以及UTC21∶00-24∶00 时间段曲线变粗.而在晚间大约UTC15∶00-21∶00 干扰消失.
|
图 1 静海台(a)和红山台(b)三分量相对观测数据 Fig. 1 Three components data of Jinghai (a) and Hongshan (b) observatory |
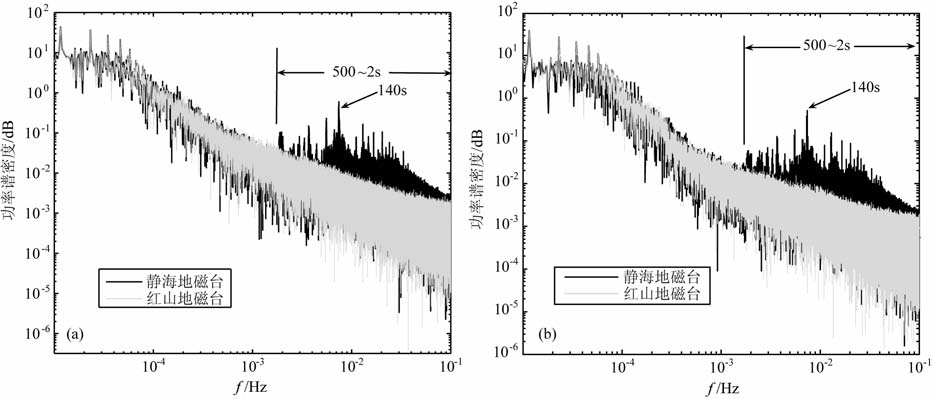
为了获得轨道交通干扰在频域内的特征,本文选取2009 年6 月-2009 年11 月期间,每月选择ΣKp指数最大的5天磁扰日和最小的5天磁静日,一共30天的垂直分量(Z)数据进行功率谱分析.如图 2所示:无论在磁扰日和磁静日,两个台站的长周期的日变规律都相当明显,其能量也最大;从500s周期直到最小周期分辨率区间,静海台出现众多的异常的干扰峰,干扰峰的最大值出现在140s周期左右.与参考台站该频率区间相比,能量增大约100dB,在高频部分干扰特征并不明显.故静海地磁台的干扰成分主要集中在10-2 Hz频率段.
|
图 2 磁扰日(a)和磁静日(b)功率谱密度图 Fig. 2 Power spectrum of geomagnetic disturbed days(a) and quiet days(b) |
本文对天津静海台与河北红山台2009 年6-11月共6个月的Z分量数据逐日进行基于Mallat算法的快速小波分解.小波分解尺度为10.分别考察这10个细节尺度上小波系数能量变化和方差的变化的差异.
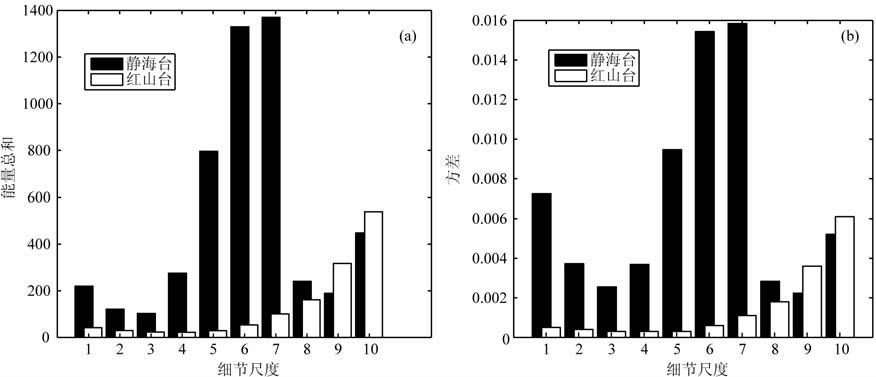
图 3为静海台和红山台垂直分量每个尺度小波系数的能量总和与方差的6个月平均值.
|
图 3 各尺度小波系数能量总和(a)和小波系数方差(b) Fig. 3 Sum of Energy of wave let coefficients (a) and variances of wave let coefficients (b) on each scale |
从图 3的分析可得:
(1) 从受干扰台站看,不管是能量总和还是方差,前7个尺度都明显大于参考台站.特别在第6和第7尺度的差异最大,几乎是同参考台站同尺度的13-15倍.通过(3)式的理论计算可知,第6 和第7尺度所对应的频率周期区间在96-192s之间.这与在功率谱分析中所得到的最大干扰频率区间对应.因此这两个尺度上的小波系数受到的干扰最大.尺度4 到尺度5 受影响强度次之,其频率周期在48-24s左右.从功率谱分析可得,这也是受干扰较为强烈的频率段.
(2) 从参考台站看,尺度1到尺度4能量总和与方差都较小,且依次有一定程度递减关系.这与仪器噪声等白噪声小波系数的分布特性相符[13].受干扰台站尽管在尺度1到尺度3 也呈现递减关系,但总能量和方差明显增大.可见轨道交通干扰也影响到小尺度区间,但影响方式还是以背景白噪声增强为主.
(3) 尺度8到尺度10 干扰程度相对较轻.特别是尺度9 以后的理论频带在767s以上,基本不受轨道交通的干扰影响.
所以对于天津静海台来说,其轨道交通干扰的小波系数主要集中在尺度4 至尺度8 之间,其中以第6和第7尺度干扰的小波系数最大.
2.4 干扰时间段的小波提取方法轨道交通的运行时间段是在凌晨开始运行,深夜停止.为突出和锐化受干扰信号边缘,获得准确的干扰起止时间段,采用小波域尺度间相关模型[14,22,23]中相邻尺度的小波系数进行相关计算.定义小波系数间的相关性计算为小波域相关系数:
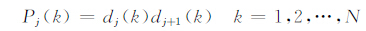
|
(4) |
为了使相关系数与小波系数间具有可比性,将Pj(t)归一化到Wjx(t),定义归一化相关系数:
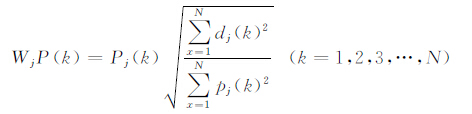
|
(5) |
最后通过判别式
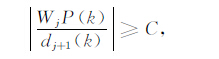
|
(6) |
(一般取C为1)确定干扰起止时间.具体步骤如下:
(1) 预处理干扰数据,去除明显的尖脉冲干扰;
(2) 对干扰数据进行离散小波快速变换,小波基选择dB8.得到第6与第7层细节尺度;
(3) 计算尺度6 与尺度7 的相关系数W6P(t)并与尺度7的小波系数进行判别,常数C取1;
(4) 通过步骤3,确定干扰起止位置.
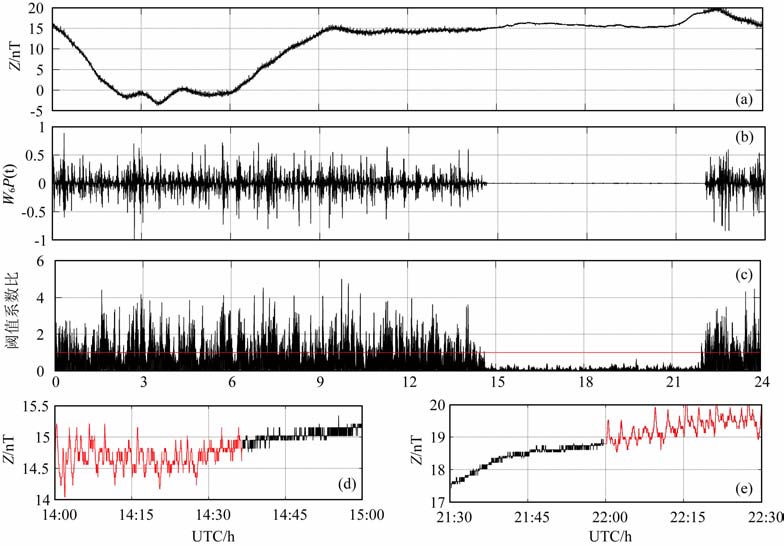
图 4a为2009年8月17号静海台Z分量干扰原始数据,为提取未受干扰时间区域,对数据进行小波域分解,得到第6 尺度和第7 尺度上的小波系数d6(k)与d7(k),计算尺度间归一化相关系数W6P(t),得到图 7b.图 7c为W6P(t)与尺度7上小波系数d7(k)的比值图,红线为阈值C=1,图 7d和图 7e为求得的干扰起止时间:干扰终止的时间大约在当地时间22时36分40秒;凌晨干扰产生时间为5时55分.
|
图 4 (a)静海台原始数据(2009-08-17);(b)尺度6与尺度7的归一化相关系数W6P(t);(c)W6P(t)与尺度7上小波系数d7(k)的比值(红色为C=1);(d)干扰停止判别效果图(红色为干扰);(e)干扰出现判别效果图(红色为干扰) Fig. 4 (a) Original signal(2009-08-17);(b) Normalized correlationW6P(t) of scale 6 and scale 7;(c)Ratio betweenW6P(t)andd7(k)(red line isC=1);(d)Distinguished noised is miss(red line is noise);(e)Distinguished noise appear(red line is noise) |

|
图 5 各尺度上的标准差的归一化 Fig. 5 Normalized value of standard deviation on each scale |
|
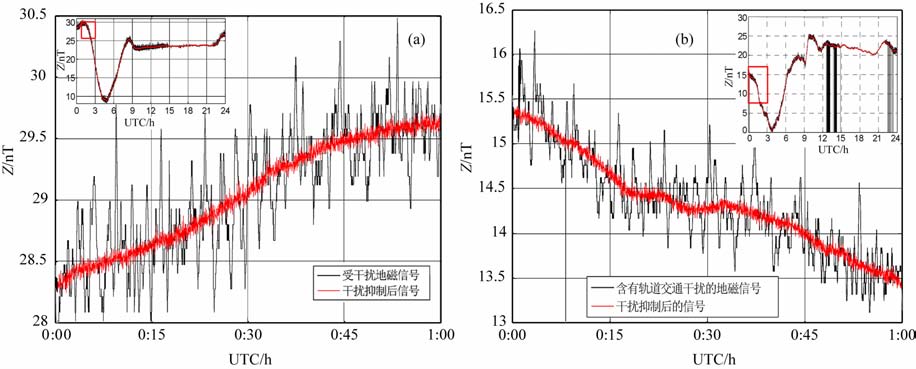
图 6 静海台干扰抑制效果图细节(a)2009-11-06ΣKp=0;(b)2009-07-22ΣKp=24. Fig. 6 Denoised geomagnetic data on Jinghai Observatory |

|
图 7 噪声抑制后的功率谱(a)磁扰日;(b)磁静日. Fig. 7 Power spectrum after noise reduction(a) Geomagnetic disturbed days; (b)Geomagnetic quiet days. |
建立准确的小波系数模型才能更有效抑制干扰.小波系数模型可分为尺度内模型、尺度间相关性模型和混合模型.在2.4节中,采用了尺度间相关性模型准确提取了干扰的起止时间段.对于干扰的抑制,本文采用尺度内模型,即判断在某尺度上小波系数的异常时,其相邻时间段内的小波系数的特征也应该考虑在内.
假设实际观测数据的数学模型如下所示:

|
(7) |
式中g(t)为需要得到的地磁相对观测数据,其物理源场是地球磁层及电离层,这其中既有规则的长周期日变信号,还有不规则的短周期波动信号;n(t)为轨道交通干扰信号,其物理场源是由轨道交通漏电的电磁场产生;ξ(t)为仪器噪声等白噪声信号受轨道交通干扰的地磁信号经过离散小波变换后,受干扰尺度同时包括了地磁相对观测信号中短周期不规则信号.因此,可以利用相邻未受干扰台站的先验知识,根据该未受干扰台站地磁信号小波系数与存在干扰台站的小波系数在同一尺度上具有不同特性的性质,构造规则,在小波域对含轨道交通干扰的信号的小波系数进行处理.以期能得到真实信号的最优估计.
根据第二节对干扰信号的分析可得:g(t)经小波变换后,长周期规则信号保留在小波变换的近似信号中,不规则扰动等短周期变化不均匀的分布在各个小波细节尺度;n(t)经过小波变换后其小波系数在102s的尺度上集中,特别在尺度5-8 上小波系数的绝对值会明显大于日变信号中不规则波动的小波系数;以仪器噪声为主的白噪声ξ(t)经过小波变换后,小波系数主要集中在尺度1-4 等小尺度上,其小波系数的均值与尺度成反比,尤其对于正态白噪声来说,随着尺度的增大,其小波系数的局部模极大值点的平均数目是上一层的一半[10,21,22].
3.2 干扰抑制策略地磁观测数据经小波分解后,每个细节尺度上受干扰与未受干扰小波系数重要程度判断是选取该尺度上的阈值关键,也是小波干扰抑制策略的关键技术.标准差σ 是估算这一波动幅度的可行指标之一[23-26].因此,通过对相邻无干扰参考台站各细节尺度上标准差σ 的考察分析,得到各尺度上的阈值,是对受干扰台站数据的小波系数进行筛选的基础.
把参考台站Z分量数据分为磁扰日与磁静日两组,各组以3h为周期对9个尺度计算全天8个标准差σ.通过每个尺度晚间(UTC15∶00-18∶00)3h标准差nnight对全天8个σ 进行按公式(8)归一化计算,对磁扰日和磁静日这两个组以95%的置信区间提取各尺度上的归一化误差阈值:

|
(8) |
图 5 中,在尺度1-3,磁静日和磁扰日的归一化误差都在10%以内,可以在该尺度区间通过nfight估算近似全天的波动幅度;尺度4-9,归一化误差有较大增幅.并且在磁静日和磁扰日也有差距.这与同纬度上空间不规则磁场的变化强度的大小有关.因此,在阈值确定上,估算各尺度上晚间未受干扰时间段的nfight, 并以相邻参考台站的通化误差大小为参考值.如式(9)所示
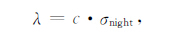
|
(9) |
式中,c值依据经验和各尺度上归一化误差的大小取值,如表 1所示:
|
|
表 1 c在个各尺度上取值 Table 1 Value ofc on each scale |
阈值施加函数体现对小波系数的处理策略,主要分为软阈值、硬阈值和半软阈值函数.在实际应用中,根据轨道交通干扰中小波系数增幅较大的特征,采用硬阈值施加函数,如(10)式所示,对大于临界阈值的小波系数直接置零:

|
(10) |
首先给出直观视觉效果.本文给出2009 年11月6日和2009年7月22日的Z分量处理结果.这两天是2009年下半年Kp指数最小和最大的两天.为了清晰展示抑制前后的细节,图 6分别给出了1h的干扰抑制数据的视觉效果.图中可以看出,垂直分量的高频细节保留充分;轨道交通干扰在时域上呈现出的多脉冲峰值特性得到有效压制;图 6b中地磁观测中的短周期波动也得到保留.同时,图 6b中仪器本身出现的短时脉冲干扰(归零现象)也能得到去除.
其次应用功率谱分析得到干扰抑制前后的频谱变化.依旧对2009年6-11月期间的磁扰日及磁静日干扰抑制后的信号进行分析,并与参考台站红山台进行比较.
抑制前后的功率谱分析表明(图 7):干扰抑制前最大100dB左右的干扰增益在抑制后消失.与参考台站比较,在该频率区间的功率谱损失在数个分贝以内.同时,原来10-2 Hz频率区间的众多异常干扰峰得到有效压制,而0.01 Hz以上高频信号几乎没有损失.
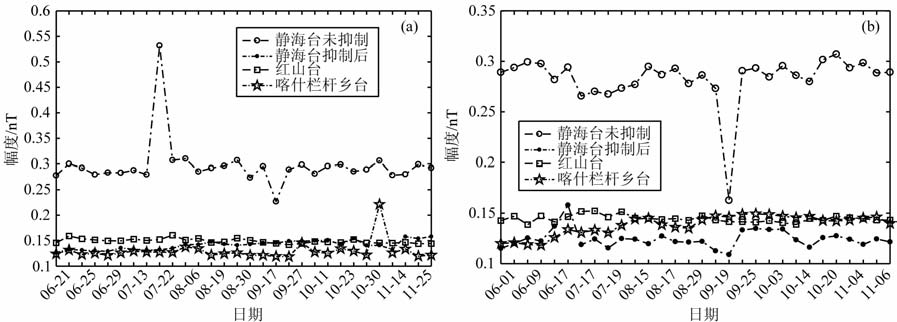
再次,本文选用基于滑动窗口的峰峰值统计图来观察干扰抑制前后的变化.滑动窗口的峰峰值统计是在实践中估算地磁噪声的一种方法.在计算中本文选用窗口大小为20,步长为10,计算全天的峰峰值.同时加入喀什栏杆乡台(地理经度76.01°E,纬度39.45°E;磁经度151.57°E,纬度30.86°N)为第二参考台站参与比较.
图 8(a, b)中虚线带空心圆曲线为受干扰的静海台观测数据的峰峰值曲线,虚线带实心圆曲线为静海台干扰抑制后的峰峰值曲线,虚线带方形与星形曲线代表两个参考台站红山台和喀什栏杆乡台.滑动窗峰峰值统计表明:天津静海台受干扰时磁静日和磁扰日全天的峰峰值的平均值在0.3nT左右,抑制后全天峰峰值下降到0.15nT 以下.而未受干扰两个参考台站全天峰峰值在0.1-0.15nT区间.静海台观测数据在干扰抑制后峰峰值特征与两个参考台很接近,与抑制前相比,降低了50%以上.最后,考虑到无法得到受轨道交通干扰台站无干扰状态下的地磁数据来计算信噪比等指标.但可使用本文抑制方法对无干扰的参考台站进行抑制,考察该方法对无轨道交通干扰地磁台站数据抑制误差大小.误差的计算公式如下:
|
图 8 磁扰日(a)和磁静日(b)峰峰值统计图 Fig. 8 Peak-peak chart on geomagnetic disturbed days(a) and geomagnetic quie tdays(b) |

|
(11) |
式中f(n)为无轨道交通干扰地磁台站原始观测信号,${\hat f}$ (n)为进行抑制后信号.
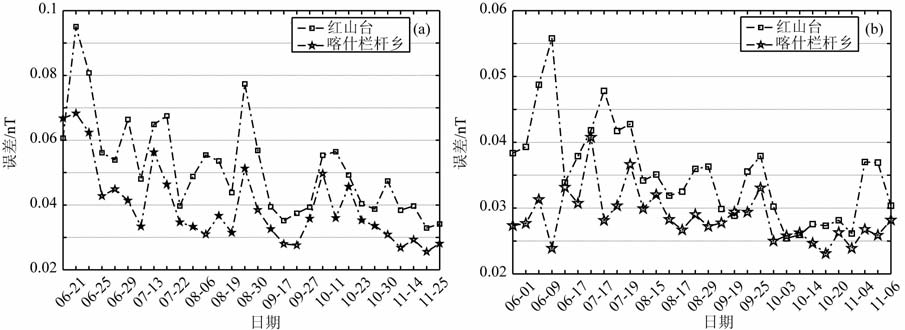
通过对未受干扰的地磁台站使用本方法进行抑制,结果表明:第一参考台站红山台的平均抑制误差在磁静日和磁扰日分别是0.04nT 和0.06nT;第二参考台站喀什栏杆乡台的平均抑制误差在磁静日和磁扰日分别是0.03nT和0.04nT.目前我国地磁台网1Hz采样相对观测仪的精度均在0.1-0.5nT.因此该方法对无轨道交通干扰的台站抑制误差小于观测仪器的精度要求.
5 讨论及结论随着小波技术的理论和应用空前发展,小波滤波方法在近年来也得到极大的发展.目前来讲,小波滤波研究主要集中在高斯白噪声假设下的模极大值重构滤波、空域相关滤波以及小波域阈值滤波,并形成了相对完整的理论体系.但对有色噪声污染的信号滤波的研究工作则刚起步.利用信号本身或者一些参考信号的先验知识对小波系数建立更准确的模型,同时在整体问题的不同层次上,把多种滤波方法有机结合起来,以取得最优滤波效果将推动该方法的发展.在滤波效果评价上,尽管大多数学者采用视觉效果以及信噪比作为评价指标,但实际工作中并不够用,这非常依赖于所要解决的具体问题的需求.本文采用小波域噪声阈值抑制模型及方法对天津静海台受轨道交通干扰的地磁数据进行抑制.采用小波域尺度间模型对晚间未受干扰时间段进行提取;采用尺度内模型对各受干扰尺度阈值进行有效估算并进行抑制.在结果分析中引入多种评价方法对抑制结果进行了多角度的对比.结果表明:在视觉效果上,高频细节保留充分,不规则短周期波动得到保留;频谱分析结果显示,干扰频率区间的功率谱损失在数个分贝以内;从基于滑动窗口的峰峰值统计来看,干扰抑制后的峰峰值特征相比抑制前下降50%,且与参考台站水平接近;使用该方法对2个无轨道交通干扰地磁台站数据抑制,平均抑制损失分别为0.05nT 和0.03nT.从以上这些评价方法可以得出,该方法能够较好地抑制轨道交通干扰并最大限度的保留地磁观测数据.
|
图 9 磁扰日(a)和磁静日(b)未受干扰台站数据经过抑制后的误差 Fig. 9 Error of denoised data from non-noise observatories (a) Geomagnetic disturbed days; (b)Geomagnetic quiet days. |
尽管采用本文方法对天津静海台2009 年下半年的受轨道交通干扰的地磁观测数据抑制结果令人满意,但此期间磁暴等极端空间天气未出现,因此本文没有讨论具有磁暴等现象的轨道交通干扰抑制的结果.这有待将来继续进行探讨.同时,为更精确地描述污染程度,进而为估算阈值提供有力的基础,三个分量地磁信号在不同尺度上的小波系数特征也需要在今后进行更详细的讨论.此外,全国各个受干扰台站的轨道交通干扰时频特征并不完全相同,该方法中的一些参数需要因地制宜做改进和调整.
随着国民经济的发展,越来越多的地磁台站观测数据受到人工电磁源的影响.地磁观测信号中干扰抑制的根本目的是更好地保障所要研究的地磁信号不受人为因素干扰.它是地磁数据分析的基础.如何能够最大程度的减少抑制带来的误差,使得抑制后的观测数据能够为防震减灾发挥作用,这是一项需要长期的、基础性的研究的任务.
致谢感谢中国地震局地球物理研究所国家地磁台网中心以及天津静海地磁台提供的地磁观测数据及受干扰情况的综述.感谢两位审稿专家的宝贵意见.
| [1] | Lowes F J. DC railways and the magnetic fields they produce-the geomagnetic context. Earth, Planets and Space , 2009, 61(8): 1-15. |
| [2] | Szarka L. Geophysical aspects of man-made electromagnetic noise in the Earth-A review. Surveys in Geophysics , 1987, 9(3): 287-318. |
| [3] | 高玉芬, 钱家栋. 地震及前兆数字观测技术规范(电磁观测). 北京: 地震出版社, 2001 . Gao Y F, Qian J D. Technology Specification of Seismic Electromagnetic Observation (in Chinese). Beijing: Seismological Press, 2001 . |
| [4] | 中华人民共和国国家质量监督检验检疫总局,中国国家标准化管理委员会.GB/T 10411-2005,城市轨道交通直流牵引供电系统.北京:中国标准出版社,2005.2-4 General Administration of Quality Supervision, Inspection and Quarantine of China, Standardization Administration of China.GB/T 10411-2005, D.C. Traction Power Supply System for Urban Rail Transit(in Chinese).Beijing: China Standard Press,2005.2-4 |
| [5] | Jankowski J,Sucksdorff C.IAGA Guide for magnetic measurements and observatory practice. International Association of Geomagnetism and Aeronomy,1996 http://ftp.bcmt.fr/pdf/IAGA-Guide-Repeat-Stations.pdf |
| [6] | Tokumoto T, Tsunomura S. Calculation of magnetic field disturbance produced by electric railway. Memoires of the Kakioka Magnetic Observatory , 1984, 20(2): 33-44. |
| [7] | Daubechies I. Ten Lectures on Wavelets. Philadelphia:Society for Industrial and Applied Mathematics,2006 http://www.oalib.com/references/16301765 |
| [8] | Asimopolos L, Pestina A M, Asimopolos N S. Considerations on geomagnetic data analysis. Chinese J. Geophys , 2010, 53(3): 765-772. |
| [9] | 潘泉, 孟晋丽, 张磊, 等. 小波滤波方法及应用. 电子与信息学报 , 2007, 29(1): 236–242. Pan Q, Meng J L, Zhang L, et al. Wavelet filtering method and its application. Journal of Electronic & Information Technology (in Chinese) , 2007, 29(1): 236-242. |
| [10] | Mallat S, Hwang W L. Singularity detection and processing with wavelets. IEEE Transactions on Information Theory , 1992, 38(2): 617-643. DOI:10.1109/18.119727 |
| [11] | Xu Y S, Weaver J B, Healy D M, et al. Wavelet transform domain filters: a spatially selective noise filtration technique. IEEE Transactions on Image Processing , 1994, 3(6): 747-758. DOI:10.1109/83.336245 |
| [12] | Donoho D L. De-noising by soft-thresholding. IEEE Transactions on Information Theory , 1995, 41(3): 613-627. DOI:10.1109/18.382009 |
| [13] | Donoho D L, Johnstone I M. Adapting to unknown smoothness via wavelet shrinkage. Journal of the American Statistical Association , 1995, 90(432): 1200-1224. DOI:10.1080/01621459.1995.10476626 |
| [14] | 胡广书. 现代信号处理教程. 北京: 清华大学出版社, 2004 . Hu G S. Lectures on Modern Signal Process (in Chinese). Beijing: Tsinghua University Press, 2004 . |
| [15] | 邱 颖.地电场观测中已知源干扰抑制研究. 北京:中国地震局地震预测研究所, 2008 Qiu Y.Research on restraining the known source interference in geoelectric field observation (in Chinese). Beijing:Institute of Earthquake Science ,CEA,2008 http://cdmd.cnki.com.cn/Article/CDMD-85405-2008129230.htm |
| [16] | 吴利辉. 基于小波分析的地铁地磁干扰抑制方法研究. 北京:中国地震局地球物理研究所, 2009 Wu L H. Study on the method based on wavelet transform theory to inhibit geomagnetic disturbance imposed by railway (in Chinese).Beijing:Institute of Geophysics,CEA.2009 http://cdmd.cnki.com.cn/Article/CDMD-85401-2010016612.htm |
| [17] | 寿海涛, 尹继尧, 于海英, 等. 佘山地磁信号的小波消噪处理. 地震地磁观测与研究 , 2009, 30(3): 85–89. Shou H T, Yin J R, Yu H Y, et al. Application of wavelet transformation to processing the noise of geomagnetic signals recorded at Sheshan seismic station. Seismological and Geomagnetic Observation and Research (in Chinese) , 2009, 30(3): 85-89. |
| [18] | Mallat S G. A theory for multiresolution signal decomposition:The wavelet representation. IEEE Transactions on Pattern Analysis and Machine Intelligence , 1989, 11(7): 674-693. DOI:10.1109/34.192463 |
| [19] | 高静怀, 汪文秉, 朱光明, 等. 地震资料处理中小波函数的选取研究. 地球物理学报 , 1996, 39(3): 392–400. Gao J H, Wang W B, Zhu G M, et al. On the choice of wavelet functions for seismic data processing. Chinese J. Geophys (in Chinese) , 1996, 39(3): 392-400. |
| [20] | Zhang L, Bao P. Denoising by spatial correlation thresholding. IEEE Transactions on circuits and Systems for Video Technology , 2003, 13(6): 535-538. DOI:10.1109/TCSVT.2003.813426 |
| [21] | 李仲宁, 罗志增. 基于小波变换的空域相关法在肌电信号中的应用. 电子学报 , 2007, 35(7): 1414–1418. Li Z Y, Luo Z Z. Spatial correlation filtering based on wavelet transformation application to EMG de-noising. Acta Electronica Sinica (in Chinese) , 2007, 35(7): 1414-1418. |
| [22] | Coifman R R, Donoho D L. Translation-invariant de-noising. Lecture Notes in Statistics.1995 http://www.oalib.com/references/16231275 |
| [23] | Donoho D L, Johnstone J M. Ideal spatial adaptation by wavelet shrinkage. Biometrika , 1994, 81(3): 425-455. DOI:10.1093/biomet/81.3.425 |
| [24] | Bruce A G, Gao H Y. Understanding wave shrink: variance and bias estimation. Biometrika , 1996, 83(4): 727-745. DOI:10.1093/biomet/83.4.727 |
| [25] | Gao H Y, Gao H, Bruce A G. Waveshrink and Semisoft Shrinkage.Technical Report.Seattle:StatSci Division of MathSoft, Inc.1995 |
| [26] | Gao H Y. Wavelet shrinkage denoising using the non-negative garrote. Journal of Computational and Graphical Statistics , 1998, 7(4): 469-488. |
 2011, Vol. 54
2011, Vol. 54


