航空电磁法自诞生以来,国际上涌现出多种新型、高性能的航空电磁测量系统,如Geotech公司的VTEM 系统[1,2],Aeroquest 公司的AeroTEM 系统,Fugro 公司的HeliGEOTEM 系统[3,4],对于新研制出的航空电磁系统,需要进行性能测试和实验,通常将测量系统挂载在飞机上,在一些“已知矿区"进行飞行实验,验证航空电磁测量系统的探测效果和分辨率;或者将几家公司生产的航空电磁系统运载到同一个“已知矿区"进行飞行实验,进行性能和探测效果的对比、互相验证.这些测试方法,由于无法准确计算出矿体的理论电磁响应,只能根据测量的剖面曲线,定性判断异常,来验证测量系统探测的有效性;并且需要将电磁测量系统、装置频繁运输到“已知矿区",因而实验费用较高,此外还须防止发生意外危险.这些实验不能模拟其他不同地电模型,不具有普遍性.
在国外发达国家中,导线环模型早已被研发人员用在时间域航空电磁探测研制过程和EM 实验中.早在1969年,加拿大A.BECKER[5,6]提出采用RC 电路,通过对电容的充放电过程来模拟大地产生的航空二次场,1984 年,A.BECKER[7]提出采用多匝线圈模拟导电球体,计算导电球体的二次场;1988年,Fitterman采用电流环进行直升机的误差校正[8],Liu[9,10]以电流环为模型,讨论了时间域航空电磁响应的多种发射电流波形影响,2007 年,A.C.Davis和J.Macnae[11,12]使用多匝线圈、采用直升机系统,对VTEM、HoistEM、AeroTEM、TEMPEST、SkyTEM 五种系统进行发射电流波形的测量,2008年,A.C.Davis 和J.Macnae[13]采用接地线圈,对HoisTEM、AeroTEM、VTEM 三种航空电磁系统进行定量校正,并未考虑补偿线圈的影响;2009年,Yin[14,15]分析和计算了半正弦波发射电流下,封闭线圈的电磁响应,进行系统异常测试.
在国内,时间域航空电磁法正反演及数据处理等方面的研究刚刚起步,吉林大学的嵇艳鞠和朱凯光在线圈姿态校正、采用神经网络进行电导率深度成像方面进行了研究[16-19],2011年,嵇艳鞠研究了异常线圈模型的电磁响应,以及覆盖层对异常线圈响应的影响.国内只有航遥中心在2008年引进一套AeroTEM 系统,由于国内缺少直升机飞行员,所以一直没有进行试飞实验.在航空电磁探测系统标定和测试方面,开展相关研究甚少,未见相关文章.
针对时间域航空电磁系统在测试时存在的不足,本文提出了一种经济、适用、快速航空电磁系统标定和测试方法,采用多匝闭合异常线圈模拟地下有限矿体,测量系统按某一角度飞越地面线圈,将测量含有几何误差的异常线圈电磁信号,与理论计算值进行比较、拟合,确定和量化几何参数和系统误差,实现航空电磁系统性能的标定、测试和校正.
2 时间域航空电磁系统测试原理根据法拉第电磁感应定律,当发射线圈中通以交变电流时,在其周围会产生交变的磁场,将一个n匝密绕的闭合线圈(以下简称为异常线圈)放置在发射线圈周围,变化的磁场在异常线圈中会产生感应电流.图 1给出了采用吊车进行航空电磁系统测试时的示意图.

|
图 1 时间域航空电磁系统测试示意图 (吊舱从外到内分别为发射、补偿、接收线圈) Fig. 1 The testing diagram of AEM system Bird (transmitter-Bucking-receiver coil) |
在图 1中,当发射线圈中磁场变化时,在接收线圈中可同时观测到四部分响应.第一部分为发射线圈激励大地所产生的瞬变电磁响应,称为大地电磁响应;第二部分为补偿线圈激励大地,补偿线圈中电流与发射线圈中电流大小相同,方向相反,产生的瞬变电磁响应与发射线圈激励的电磁响应符号相反,通过设计补偿线圈半径的大小,可以在发射线圈中心点将一次场补偿掉95%,使得接收点的一次场仅有5%左右;第三部分为发射线圈中磁场变化激励异常线圈,异常线圈自身产生的电磁响应,称为异常线圈响应;第四部分为异常线圈中产生的感应电流作为新的激励源,激励大地所产生的三次电磁响应,称为三次响应.
图 2给出了异常线圈中的感应电流波形.在发射电流为零期间,感应电流呈指数规律变化,与有限导体产生的瞬变电磁信号衰减规律相同,利用这个特点,我们采用异常线圈的电磁信号来模拟地下有限导体的瞬变电磁信号.

|
图 2 发射电流(上)和异常线圈感应电流(下)波形 Fig. 2 Transmitter current wave form and induced current wave form of anomaly loop |
发射线圈和补偿线圈激励的大地响应,在数据后期拟合处理时可按背景场处理.当发射电流为上百安培时,异常线圈中感应电流一般在毫安级,将测试实验选在非良导大地区域进行,则三次响应完全可以忽略.因此,在对实测数据进行拟合时,只需要计算地面闭合异常线圈产生的电磁响应即可.
3 异常线圈的电磁响应计算发射线圈交变磁场在异常线圈中产生的感应电动势为[19]
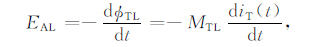
|
(1) |
式中iT(t)为发射电流,ΦTL 为发射线圈的磁通量,MTL为发射线圈与异常线圈之间的互感系数.异常线圈可以用一个等效电感和等效电阻进行近似,在异常线圈中产生感应电流,用等效回路的瞬态方程描述为
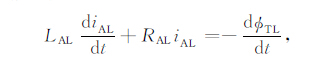
|
(2) |
式中iAL为异常线圈的感应电流,RAL 为线圈电阻,LAL为线圈的电感.
将(1)代入(2)式中,有

|
(3) |
方程(3)采用拉氏变换求解,感应电流写为

|
(4) |
地面线圈中感应电流为线圈的脉冲响应与发射电流导数的卷积.其中s为拉普拉斯算子,τL 为异常线圈的时间常数,与线圈的材料、电气性能有关,其表达式为
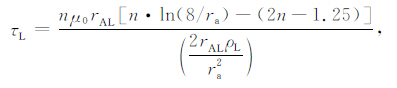
|
(5) |
式中μ0 为磁导率,n为异常线圈匝数,rAL为线圈半径,ra 为导线半径,ρL 为导线电阻率.对于任意位置的两线圈之间的互感写为

|
(6) |
式中r1 和r2 为两圆线圈的半径,Φ1 为积分元dΦ1 与x轴夹角、Φ2 为积分元dΦ2 与x轴夹角,z1 为线圈的中心坐标,z为两线圈的高度.
在异常线圈中产生的感应电动势为

|
(7) |
式中MRL为接收线圈与异常线圈间的互感系数.
将(4)式代入上式,有
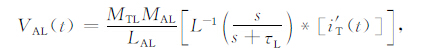
|
(8) |
进行逆拉氏变换和卷积计算,整理有
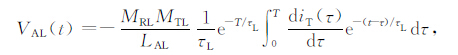
|
(9) |
式中T为梯形波的周期.当发射电流为图 1所示的梯形波时,整理有

|
(10) |
式中I为发射电流幅值,T1 为电流上升时间,T2 为电流下降时间,T3 为发射电流宽度.
将(5)式和(9)式代入(4)式和(8)式中,采用高斯数值积分,就可以实现闭合异常线圈的感应电流和感应电动势的数值计算.
将(10)式进行简化,异常线圈电磁响应写为
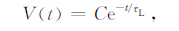
|
式中C为与几何参数有关的常数,其中τL 为异常线圈的时间常数,式中

|
对于有限规模的导体,在晚期的瞬变电磁响应变化可以写为[19]

|
(12) |
式中K1 为常数,其中τd 为导体的时间常数.通过对比(11)和(12)式可以得出结论:异常线圈的电磁响应和有限导体的电磁响应表达式相同,只要异常线圈的时间常数和有限导体的时间常数相同,就可以用异常线圈来模拟有限导体.
4 确定异常线圈的τL 值为了准确模拟有限导体的响应,需要确定相对应的异常线圈τL 值.不同有限导体与时间常数τd的经验值之间对应关系在表 1中列出[20,21],有经济价值的矿体的时间常数一般大于2ms, 表 1为确定异常线圈的τL 值提供了参考依据.
|
|
表 1 有限导体与时间常数的对应表 Table 1 Finite orebody and corresponding time constant |
异常线圈的τL 值与所采用铜导线的电气特性有关,即与线圈自感和电阻有关.我们选择了野外实验中常用的几种铜导线进行研究.图 3 给出了异常线圈τL 值随线圈半径r(相当于公式(5)中的rAL)、匝数变化的情况,图 3a给出了异常线圈单匝时,τL值随线圈半径变化.对于单匝异常线圈,当半径增大到100m 时,选用10mm2 铜导线,τL 值也只有1.3ms, 如果选用截面积再大的铜导线,导线的重量太重,不利于野外施工.图 3b给出了异常线圈半径一定时,τL 值与随线圈匝数变化特征,线圈匝数增加,τL 值线性增大.

|
图 3 (a)异常线圈τL 值随半径(单匝)变化曲线;(b)异常线圈τL 随线圈匝数变化曲线(r=10m) Fig. 3 (a) The curve ofτL value for anomaly loop of different wire with radius varies(single turn);(b) The curve ofτLvalue for anomaly loop of different wirewithturnvaries(r equals 10m) |
结合表 1 中导体的时间常数,以及图 3a和图3b中τL 值的变化,合理设计异常线圈参数,就可以模拟不同导电性的矿体.如模拟τd 值为4 ms的良导矿体,可以选用10mm2 铜导线绕4匝、半径为10m的异常线圈,也可以选用2mm2 的铜导线绕20匝、半径为10m 的异常线圈,应该说前一种线圈性能价格比更高.在野外实施时,尽可能在满足施工轻便、快捷、经济等需求前提下,确定合适的异常线圈参数.
在确定异常线圈的τL 值时,不仅要符合实际矿体的时间常数,而且还要适宜航空电磁系统观测.结合实际研制的航空发射-接收线圈参数:发射线圈半径为7.5m, 匝数为5,发射电流184A,吊舱高度为8m, 补偿线圈半径为1.5m, 匝数为1,接收线圈半径为0.55m, 匝数为120.异常线圈半径为7.5 m、匝数为4.计算了异常线圈电磁响应随τL 值变化曲线,如图 4所示.从图可见τL 值小于0.5 ms时,响应衰减很快,在0.2ms之后就进入了噪声区,这为选择系统测试地点提供了依据.测试时应选择大地时间常数小于0.5ms的地区进行,尽可能减小大地对测试结果的影响;τL 值大于5 ms后,响应衰减缓慢,幅值较小,不利于测量.实际测试时,建议异常线圈的τL 在2-5ms范围最佳.

|
图 4 不同τL 值的异常线圈电磁响应 Fig. 4 Anomaly loop electromagnetic responses of DifferentτLvalue |
在野外实验时,仅知道异常线圈的τL 值远不够,还需要确定异常线圈铺设时的几何参数.为了模拟实际有限矿体的异常,在测试时,希望测量的剖面曲线中能够观测到单峰正异常,单峰正异常的大小和异常宽度与线圈的半径、匝数等直接相关.
我们计算了异常线圈匝数一定、半径不同时,发射-接收装置位于异常线圈中心时的电磁响应,如图5a所示,电磁响应随异常线圈半径增大而增大;但当异常线圈半径接近发射线圈半径时,互感最大,响应达到最大;异常线圈半径大于发射线圈后,响应开始减小.由于补偿线圈的作用,当线圈半径为10 m时,响应最大;半径为7.5m 时响应次之.图 5b给出了响应随异常线圈匝数变化曲线,线圈匝数越少,曲线衰减越快,动态范围越大,早期信号幅值越大,晚期响应越小;反之亦然.图 5c给出了异常线圈响应随观测高度的变化曲线,观测高度越高,响应幅值越小;反之亦然.

|
图 5 异常线圈响应随线圈半径(a)、线圈匝数(b)、观测高度(c)的变化 Fig. 5 The response with the loop radius(a),the loop turn (b)and the loop flight altitude(c)varies |
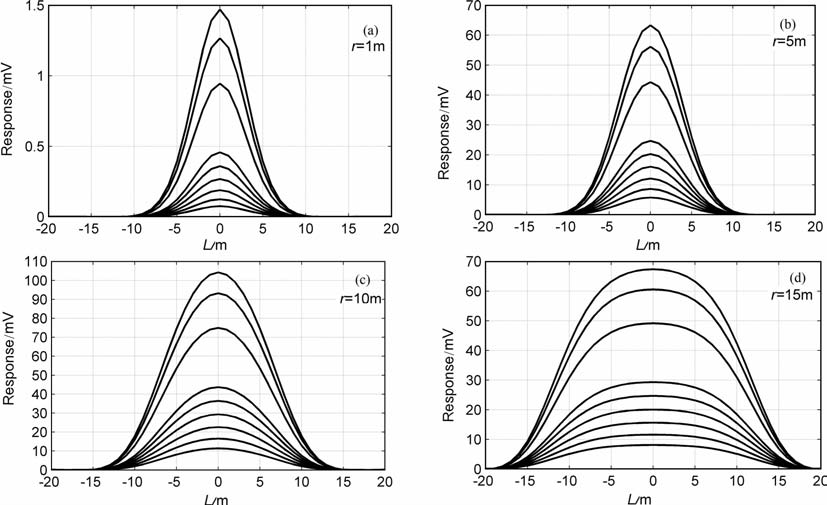
图 6给出了当异常线圈放在剖面曲线的0m 位置时,异常线圈不同半径时的响应剖面曲线,表 3给出了剖面曲线的特征值.线圈半径越大,τL 值越大,剖面曲线的半极值宽度越宽,当半径接近发射线圈半径时,异常的峰值最大.异常线圈半径为1 m 时,虽然异常半极值宽度为3.5 m, 但产生的响应幅值太小,峰值最大只有0.07 mV,不利于测量系统分辨,容易受到噪声干扰;异常线圈半径大于10m表 3 不同线圈半径的异常特征值(4匝)后,异常半极值宽度增大,但响应幅值变小.只有异常线圈半径接近发射线圈半径时,异常幅值最大,宽度大约为异常直径的75%左右.
|
图 6 剖面曲线随异常线圈半径变化图(L 为剖面曲线距离) Fig. 6 The profile curve with the anomaly loop radius varies(0.18、0.55、0.97、1.6、2.9、4.3、5.1、6.5、8.7 ms) |
|
|
表 3 不同线圈半径的异常特征值(4匝) Table 3 The anomaly characteristics of anomaly loop radius |
通过上面的分析和研究,设计异常线圈的参数为:采用10mm2 的铜导线,半径为7.6m, 匝数为4匝,时间常数为3.55ms.
6 测试实验结果及分析2010年在长春市市郊附近的大鹅岛,采用设计的异常线圈进行了航空电磁系统测试和标定实验.大鹅岛场地空旷,偏离人文设施较远,电磁噪声相对较小,并预先采用了地面TEM 系统进行测量,确定实验场地没有其他低阻异常.
野外实验的示意图如图 1,测试时将发射线圈、接收线圈、补偿线圈固定在吊舱上,采用吊车将其吊起8m 高,先测量含有吊车的大地响应;然后在地面铺设设计的异常线圈,吊车转动测量,此时获得含有异常线圈和大地、吊车的电磁响应.数据后期处理时,忽略三次感应响应,将大地、吊车的响应从实测数据中进行分离,获得纯异常线圈的感应信号.采用下面拟合方程将实测数据与理论计算值进行拟合,确定系统误差和几何参数误差:

|
(11) |
式中Vi(x,y,h,k)为理论计算值,Vp(x+Δx,y+Δy,h+Δh,k+Δk)为实测数据,x为飞行水平位置,Δx为飞行水平偏移误差,y为飞行垂直位置,Δy为飞行垂直偏移误差,h为飞行高度,Δh为飞行高度误差,k为线圈放大倍数,Δk为线圈放大倍数偏差,N为取样道数,通过(11)式拟合可以确定几何参数误差Δx,Δy,Δh,Δk等参数.
图 7a给出了吊车转动测量时,发射-接收线圈在异常线圈中心点处,实测数据与理论值拟合的结果.实验设计时飞行高度为8m, 但是通过采用(11)式拟合,确定拟合参数高度误差Δh=0.4m, 水平偏移误差Δx=0.2 m, 放大倍数偏差Δk=0.7.图 7b给出了剖面曲线按中心点拟合参数进行拟合后与计算值对比结果.从图可见,各点拟合精度有差异,但是实测数据剖面曲线出现的单峰正异常的位置与理论计算值一致,而且异常半极值宽度接近,验证了仪器系统的测量准确性和有效性.由于采用吊车进行系统测试时,没有安装GPS和姿态参数等辅助测量装置,因此GPS信息和姿态角不能准确记录,而且吊车转动速度由驾驶员控制,无法记录,因此,进一步精细处理时,应按不同的几何参数进行拟合,确定系统误差和几何参数误差.当采用实际直升机进行飞行测试,只要记录了GPS信息、飞行速度、线圈姿态等信息,就可以通过拟合方程确定系统的几何误差参数.

|
图 7 (a)异常线圈中心衰减曲线实测数据与计算值对比(Δh=0.4m,Δx=0.2m,Δk=0.7);(b)拟合后实测数据(实线)和计算值(虚线)的剖面曲线对比 Fig. 7 (a)Decay curve measured of anomaly loop center compared with the calculated curve(Δh=0.4m,Δx=0.2m,Δk=0.7);(b) Profile curve for delay channels comparison of the measured fitting (dots) and the calculated (dashes) |
图 8a给出了测量装置位于异常线圈中心时,实测数据与计算值的绝对误差曲线,在早期误差较大,晚期误差小,单点实测数据的平均绝对误差为0.6mV,最小误差为0.05 mV,最大误差出现在早期,主要由接收线圈的频率特性引起.图 8b给出了在异常线圈中心测量的相对误差曲线,最大误差在1%内,通过拟合后,相对平均误差在早期完全满足野外勘探需求.
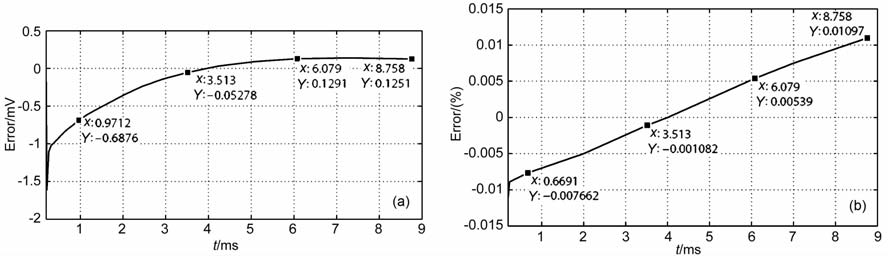
|
图 8 在异常线圈中心数据各时间道的系统误差(a)和相对误差(b) Fig. 8 The system error(a) and relative error (b) of each delay channel in anomaly loop center |
通过前面研究结果表明,在非良导大地(时间常数小于0.5ms)区域铺设闭合异常线圈,改变线圈的电性和几何参数,来模拟时间常数为2-5 ms的有限导体的电磁响应,将测量的异常线圈感应信号和理论计算值进行拟合,即可实现时间域航空电磁测量系统(包括发射机、接收机、发射-接收-补偿线圈)的测试和标定.采用异常线圈测试AEM系统是一种准确、快速、经济可行和有价值的方法,而且线圈铺设便捷,几何参数和电性参数调整灵活,可用于检测任何时间域电磁测量系统,验证电磁系统的有效性,为将来采用直升机进行实际飞行测量奠定了基础和提高了技术保障.
致谢感谢吉林大学地球信息探测仪器教育部重点实验室提供了研究平台,感谢吉林大学时间域航空电磁组的全体成员,感谢殷长春研究员的通信指导,感谢两位审稿者对该文的快速认真审稿.
| [1] | Fountain D. 60 years of airborne EM-focus on the last decade. In: AEM 2008-5th Internatio nal Conference on Airborne Electromagnetics. Finland: Haikko Manor, 2008 |
| [2] | 张昌达. 航空时间域电磁法测量系统:回顾与前瞻. 工程地球物理学报 , 2006, 3(4): 265–273. Zhang C D. Airborne time domain electromagnetics system: look back and ahead. Chinese Journal of Engineering Geophysics (in Chinese) , 2006, 3(4): 265-273. |
| [3] | Witherly K, Irvine R, Morrison E. The Geotech VTEM time domain helicopter EM system. In: 'ASEG 17th Geophysical Conference and Exhibition, Sydney. 2004 |
| [4] | Balch S J, Boyko W P, Paterson N R. The AeroTEM airborne electromagnetic system. The Leading Edge , 2003, 22(6): 562-566. DOI:10.1190/1.1587679 |
| [5] | Grant F S, West G F. Interpretation Theory in Applied Geophysics. New York: McGraw-Hill, 1965. 489-495 |
| [6] | Becker A. Simulation of time-domain, airborne, electromagnetic system response. Geophysics , 1969, 34(5): 739-752. DOI:10.1190/1.1440044 |
| [7] | Becker A, DeCarle R, Lazenby P G. Simplified prediction of transient electromagnetic response. Geophysics , 1984, 49(7): 913-917. DOI:10.1190/1.1441736 |
| [8] | Fitterman D V. Sources of calibration error in helicopter EM data. Exploration Geophysics , 1988, 29(2): 65-70. |
| [9] | Liu G M, Aasten M W. Fast approximate solutions of transient EM response to a target buried beneath a conductive overburden. Geophysics , 1993, 58(6): 810-817. DOI:10.1190/1.1443466 |
| [10] | Liu G. Effect of transmitter current waveform on airborne TEM response. Exploration Geophysics , 1998, 29(2): 35-41. DOI:10.1071/EG998035 |
| [11] | Stolz E M, Macnae J. Evaluating EM waveforms by singular-value decomposition of exponential basis functions. Geophysics , 1998, 63(1): 64-74. DOI:10.1190/1.1444328 |
| [12] | Macnae J, Davis A C. Surface loop monitoring of airborne electromagnetic systems. SEG Int'l Exposition and 74th Annual Meeting, Denver, Colorado, 2004 http://cn.bing.com/academic/profile?id=1985829806&encoded=0&v=paper_preview&mkt=zh-cn |
| [13] | Davis A C, Macnae J. Quantifying AEM system characteristics using a ground loop. Geophysics , 2008, 73(4): F179-F188. DOI:10.1190/1.2943189 |
| [14] | Yin C, Smith R S, Hodges G, et al. Modeling results of on-and off-time B and dB/dt for time-domain airborne EM systems. 70thAn-nual Conference and Exhibition, Extended Abstract, H048, EAGE, 2008. 1-4 |
| [15] | Yin C C, Hodges G. Wire-loop surface conductor for airborne EM system testing. Geophysics , 2009, 74(1): F1-F9. DOI:10.1190/1.3008055 |
| [16] | 嵇艳鞠, 林君, 关珊珊, 等. 直升机航空TEM中心回线线圈姿态校正的理论研究. 地球物理学报 , 2010, 53(1): 171–176. Ji Y J, Lin J, Guan S S, et al. Theoretical study of concentric loop coils attitude correction in helicopter-borne TEM. Chinese J. Geophys. (in Chinese) , 2010, 53(1): 171-176. |
| [17] | 朱凯光, 林君, 韩悦慧, 等. 基于神经网络的时间域直升机电磁数据电导率深度成像. 地球物理学报 , 2010, 53(3): 743–750. Zhu K G, Lin J, Han Y H, et al. Research on conductivity depth imaging of time domain helicopter-borne electromagnetic data based on neural network. Chinese J. Geophys. (in Chinese) , 2010, 53(3): 743-750. |
| [18] | 嵇艳鞠. 浅层高分辨率全程瞬变电磁系统中全程二次场提取技术研究. 长春: 吉林大学, 2004 Ji Y J. All -time secondary electromagnetic field extraction in high resolution transient electromagnetic system for subsurface imaging (in Chinese) . Changchun: Jilin University, 2004 http://cdmd.cnki.com.cn/Article/CDMD-10183-2004100119.htm |
| [19] | 嵇艳鞠, 栾卉, 李肃义, 等. 全波形时间域航空电磁探测分辨率. 吉林大学学报(地球科学版) , 2011, 41(3): 885–891. Ji Y Y, Luan H, Li S Y, et al. Resolution of full-waveform airborne TEM. Journal of Jilin University (Earth Science Edition) (in Chinese) , 2011, 41(3): 885-891. |
| [20] | Nabighian M N. Electromagnetic Methods in Applied Geophysics.Vol. 1 of Investigations in Geophysics. Society of Exploration Geophysicists, Tulsa, 1987. 5-45 |
| [21] | Balch S J, Boyko W P. The AeroTEM airborne electromagnetic system. Aeroquest Limited, Milton, Ontario, Canada. N. R. Paterson, Paterson, Grant and Watson Limited, Toronto, Ontario, Canada, 2003 http://cn.bing.com/academic/profile?id=2051950289&encoded=0&v=paper_preview&mkt=zh-cn |
 2011, Vol. 54
2011, Vol. 54




