2. 中国科学院研究生院, 北京 100049;
3. 中国地质大学(武汉)地球物理与空间信息学院, 武汉 430074;
4. 国土资源部海洋油气与环境地质重点实验室, 青岛 266071;
5. 青岛海洋地质研究所, 青岛 266071
2. Graduate University of the Chinese Academy of Sciences, Beijing 100049, China;
3. Institute of Geophysics & Geomatics, China University of Geosciences, Wuhan 430074, China;
4. The Key Laboratory of Marine Hydrocarbon Resource and Environmental Geology, Ministry of Land and Resources, Qingdao 266071, China;
5. Qingdao Institute of Marine Geology, Qingdao 266071, China
大地电磁测深法(Magnetotelluric sounding, 简称MT)通过观测地面上天然电磁场的变化达到研究地层电学性质的目的.观测资料的反演是该方法的核心问题之一.目前一维和二维反演已非常成熟,三维正反演也在进行深入的研究.一维反演方法主要有高斯-牛顿法、马夸特法、广义逆反演法等,二维反演方法主要有快速松弛反演法[1]、奥可姆反演法[2,3]、非线性共轭梯度反演法[4]等.但是上述方法属于线性化算法,容易依赖于初始模型、陷入局部极小等.因此,一些成熟的完全非线性反演方法如模拟退火法[5]、遗传算法[6]等,由于其无需求解偏导数矩阵,解除了对初始模型的依赖性,被引入到MT 的反演中,取得了比较好的效果.
量子遗传算法(Quantum Genetic Algorithm, 简称QGA)是量子计算和遗传算法相结合的优化算法,由于其基于量子概率编码的并行性和隧道效应,以及量子门的定向更新,可在一定程度上提高计算效率和减小陷入局部极值的可能性,因此,该算法已广泛应用于电力[7-9]、图像处理[10-12]等领域.罗红明等[13]已将量子遗传算法成功地应用于一维大地电磁测深反演,取得了比较好的结果.
量子遗传算法虽然是一种高效的并行算法,但它仍具有容易陷入局部极值,收敛速度慢等不足,对此,研究者们提出了诸如多宇宙和量子变异[14,15]、分层分组[16]、群体灾变和自适应搜索网格[17]、基于信息正反馈的岛屿模型和进化方程[18]、基于量子位Bloch坐标[19]、角度编码染色体[20]等思想对量子遗传算法进行了改善.
本文在对常规量子遗传算法认真研究的基础上对算法进行了有效的改进,并将其引入基于子空间的二维MT 反演,模型试验和实测资料反演均证明了改进量子遗传算法对二维MT 反演的可行性和有效性.
2 量子遗传算法及其改进 2.1 量子遗传算法量子遗传算法中,量子信息由量子位表示.如式(1)所示.
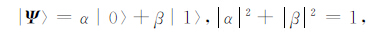
|
(1) |
染色体可表示为:

|
(2) |
其中,Qjt代表第t代、第j个个体的染色体,m为染色体的基因个数,k为编码每一个基因的量子比特数.
在量子遗传算法中采用量子门进行更新.在此,我们选择量子旋转门G:
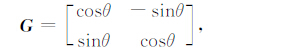
|
(3) |
其中,θ 为量子门的旋转角,取值为:
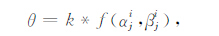
|
(4) |
式中,k是搜索步长,与算法收敛速度有关.函数(fαjt,βjt)的作用是使算法朝着最优解的方向搜索,取值如表 1所示.其中djOpt为当前搜索到的最佳解的第j个量子概率幅[αjOpt,βjOpt]T 元素的乘积,即djOpt=αjOptβjOpt,其相位为
|
|
表 1 优化搜索函数f(αjt,βjt)取值表 Table 1 The value of optimizing search functionf(αjt,βjt) |

|
(5) |
式中,t为进化过程中当前的代数,tji(t)为当前代的第i个个体的第j个量子位的概率幅,G(i,j,t)为在当前的量子旋转门,tji(t+1)为更新后的量子位的概率幅.
2.2 量子遗传算法的改进根据对传统量子遗传算法的细致分析和讨论,对算法进行以下改进:
(1) 对于旋转角θ 中搜索步长k的改进:传统量子遗传算法中,搜索步长取为k=aexp(-t/maxt),其中t为进化代数,a为任意指定的常数,一般由试验获得.本文考虑借鉴模拟退火算法中退火温度的思想加速收敛速度,同时引入波动阻尼振荡,降低算法陷入局部极值而无法自动跳出的可能性.具体令k=2π0.935$\dot{t}$rt,其中,t为进化代数,rt为一个0.8-1.2的随机数.两种取值方案的收敛速度对比如图 1所示,可以看出,在相同的进化代数内,本文提出的方案收敛速度更快.

|
图 1 传统量子遗传算法和改进量子遗传算法搜索步长曲线对比图 Fig. 1 The comparis on between the conventional QGA and improved QGA |
(2) 量子遗传算法是量子计算与遗传算法相结合的产物,也是一种模拟自然界物种进化机制的启发式搜索算法,传统量子遗传算法中,每次迭代只允许产生一个后代个体,不仅大大降低了染色体中所蕴含信息的利用率,也不符合自然界的物种法则,因此,本文借鉴“多胞胎"的概念,允许量子染色体产生不只一个、而是两个甚至多个后代个体,这些个体具有非常高的相似度,我们认为只有其中一个或少数几个量子位不同,后代个体之间比较拟合度,只保留最优秀的个体,作为更新后的染色体,这样就可以较充分地利用每条量子染色体所携带的基因信息,提高算法性能.
(3) 常规量子遗传算法容易陷入局部极值,很大程度上是由于搜索空间较大且固定,所需搜索的变量大大增加,在染色体量子位进化到0 或1 时仍未搜索到全局最优值,因此,引入弹性搜索空间机制,每次迭代时自动调整搜索空间,很大程度上抑制了常规量子遗传算法易早熟收敛的缺点.
改进量子遗传算法的具体流程如下:
①初始化:确定种群和记忆库的大小、遗传代数,根据各参数的取值范围计算量子位数目,所有的量子位概率幅绝对值均取$1/\sqrt 2 $,表示所有初始搜索状态以等概率叠加;
②测量:对每个个体的每个量子概率幅进行观测,得到相应的二进制.具体过程为:随机产生一个[0,1]的数,若它小于概率幅的平方,则测量结果取0,否则取1;
③解码:将当前测量得到的二进制串根据参数的弹性取值范围进行解码,得到各参数对应的十进制值;
④正演:对每个个体的参数组合进行正演计算,得到各个体的适应度值;
⑤排序、更新:根据适应度值将记忆库中个体与当前个体综合排序,选出最优个体,判断是否满足终止条件,若满足,则停止迭代,否则,执行下一步,同时对记忆库进行更新;
⑥种群个体更新:根据式(3)计算量子旋转门,并对种群中的个体进行更新,产生“多胞胎",优胜劣汰;
⑦进入下一代循环,算法转至步骤(2)继续执行,直到满足终止条件或达到最大循环代数.
2.3 改进量子遗传算法的效果验证为了验证改进量子遗传算法的效果,我们首先选用一个大地电磁一维两层D型模型进行反演,与表 2 反演的模型空间和分辨率表 3 两层D型模型常规量子遗传算法和改进量子遗传算法反演结果常规量子遗传算法的反演结果进行比较.
|
|
表 2 反演的模型空间和分辨率 Table 2 Model space and resolution |
|
|
表 3 两层犇型模型常规量子遗传算法和改进量子遗传算法反演结果 Table 3 Inversion results using conventional QGA and improved QGA for two-layer (D-type) model |
模型参数为:ρ1 =100Ωm,ρ2 =10Ωm,h1 =2000m, 反演的模型空间和分辨率如表 2 所示.迭代次数为50,种群个体数为10,变异概率0.01,“多胞胎"概率0.1.取30 次反演结果平均值作最终结果,如表 3所示,每次改进效果也在表 3中一一列出.表 3中,对比平均值和最优值,每一步对常规量子遗传算法的改进都可以得到更好的结果,最终的总体改进效果也说明了同样的问题.
对一个一维四层HK 型模型进行反演,以验证对算法的改进效果.模型参数为:ρ1=100Ωm,h1=600m,ρ2=20Ωm,h2=1500m,ρ3=300Ωm,h3=3000m,ρ4=10Ωm.迭代次数为100,种群个体数为20,变异概率0.01,“多胞胎"概率0.1,分辨率1.取30次反演结果平均值作最终结果,如表 4所示.对比表 4中各参数的反演结果,由于等值性的存在,第三层的电阻率不管常规方法还是改进方法都有较大的误差,但对其他参数结果来说,改进量子遗传算法得到的结果更接近真实值.
综上两个模型的反演试验,可以认为对常规量子遗传算法的改进是成功的.
3 基于子空间的二维MT 反演 3.1 子空间二维反演的思路子空间思想最初由Kennett[21]引入地球物理反演,Oldenburg[22]对其进行了改进.子空间方法只需对一个维数等于子空间维数的矩阵进行反演,这是该方法与传统的高斯牛顿法相比的主要优点所在.本文只考虑最简化条件,即一个测点对应一列网格,于是子空间的大小即是参与反演的网格列数的多少,当子空间的维数为一维时,就是传统的一维反演,若子空间维数增加到与全部网格列数相同时,表 4 四层HK型模型传统量子遗传算法和则演变为传统的全空间反演.现以如图 2 所示的二维模型,即一条测线为例说明本文子空间反演的思路.若在此测线上有10 个测点,则将地面以下需反演空间剖分为10列网格,子空间每次向前滑动一个测点.如第一次反演时子空间为1、2、3测点,第二次时就变为2、3、4,依次滑动下去,直到最终反演结束.因此,本文的子空间方法实质上属于滑动子空间方法,可以保证除边界外的每列网格都能被反演至少两次,充分利用每个测点的观测数据所包含的除测点正下方网格外的子空间其他网格的网格参数信息,反演完成后对结果进行一定的处理,可以保证反演结果的准确性.同时,在反演中,只对子空间内中间测点的视电阻率观测数据进行拟合,保留中间网格的结果作为一部分,其他网格的结果作为另一部分,最终的反演结果则按照一定的比例叠加,叠加后的结果更准确、更合理.
|
|
表 4 四层犎犓型模型传统量子遗传算法和改进量子遗传算法反演结果 Table 4 Inversion results using conventional QGA and improved QGA for four-layer (HK-type) model |

|
图 2 二维模型示意图 Fig. 2 The sketch map of the 2D model |
选取目标函数为:

|
(6) |
其中,Φd(m)为数据拟合差,Φm(m)为模型拟合差,μ 为正则化因子.
如图 3 所示,地下1km 深度处存在一个低阻异常体,电阻率为10Ωm, 尺寸为1km×1km, 背景为100Ωm.选取如下所示的20 个频点,分别为:100、75、50、25、12.5、10、7.5、5、2.5、1.25、1、0.75、0.5、0.25、0.125、0.1、0.075、0.05、0.025、0.01,单位为Hz.网格采用不等间距剖分,总体剖分为20×16的网格,异常体剖分为6×4的网格.

|
图 3 模型示意图 Fig. 3 The sketch map of the model′s position |
网格具体剖分为:
Y轴(m):5000 2000 1000 500 250 250 250 250 250 250 250 250 500 1000 2000 5000
Z轴(m):100 100 300 300 100 100 100 100 300 300 100 100 100 100 300 500 1000 3000 5000 10000
TE 模式下所加空气层网格剖分(从上到下)依次为:10000 5000 3000 1000 500 300 100 100.单位为m.

|
图 4 TE(a)和TM(b)模式视电阻率等值线图(Ωm) Fig. 4 The isopleths map of the apparent resistance for TE (a)and TM (b)(Ωm) |
反演时需确定子空间的大小,即同时反演测点的个数.
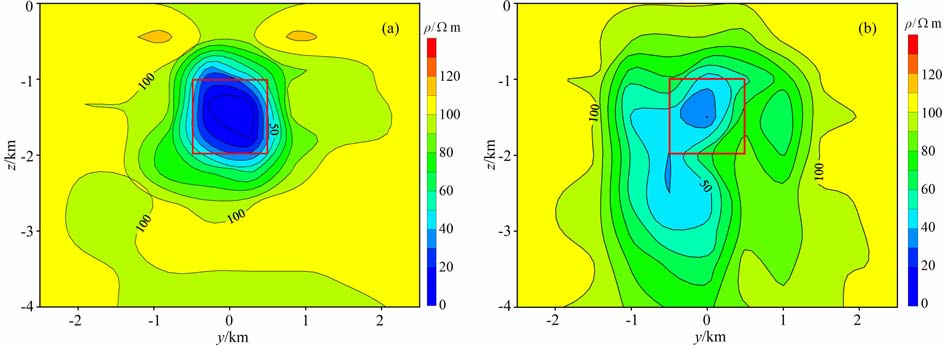
对视电阻率等值线图进行分析.在图 4b中,异常体的横向影响范围大致为-1500-1500 m, 而异常体的横向尺寸为1000 m, 也就是说,异常体的横向影响范围为其本身横向尺寸的3 倍左右距离,同时考虑子空间的对称性,初步确定子空间的大小为5个测点或7个测点的范围.同时,为更进一步验证改进量子遗传算法相对于传统量子遗传算法的高效性,分别对模型进行两种算法的反演.子空间为5测点大小进行反演时,改进和传统量子遗传算法各反演参数共同取值如下:种群个体数20,遗传代数100,变异概率0.01,产生“多胞胎"概率0.1,分辨率1,反演结果如图 5所示.
|
图 5 子空间为5测点大小时的改进量子遗传算法 (a)和传统量子遗传算法(b)反演结果红色矩形代表异常体真实位置. Fig. 5 The inversion results using improved (a)and conventional (b) QGA,respectively The red rectangle shows the true position of the anomalous body. |
子空间为7测点大小进行反演时,量子遗传算法各反演参数取值如下:种群个体数30,遗传代数150,变异概率0.01,产生“多胞胎"概率0.1,分辨率1,反演结果如图 6所示.
|
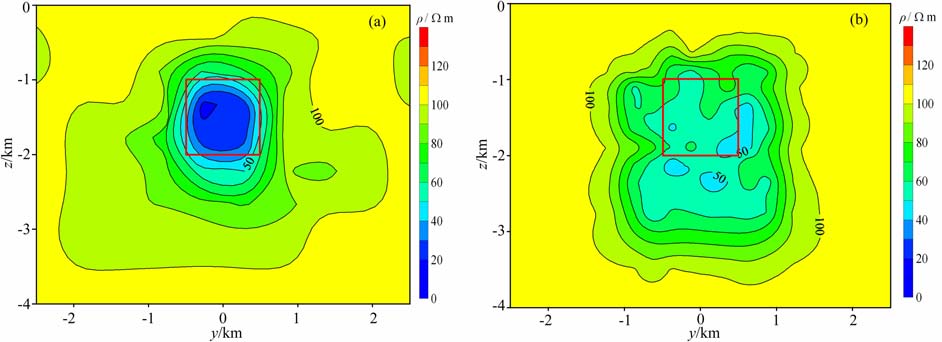
图 6 子空间为7测点大小时的改进量子遗传算法 (a)和传统量子遗传算法(b)反演结果红色矩形代表异常体真实位置. Fig. 6 The inversion results using improved (a) and conventional (b)QGA,respectively The red rectangle shows the true position of the anomalous body. |
对比图 5a和5b,可以看出,图 5b 中显示有大片低阻区域,电阻率值也较高,表明算法没有完全收敛,说明改进算法的效果要优于传统算法.图 6中也显示有类似特征.
综合图 5和图 6,可以看出,子空间不管选为5个测点大小还是7 个测点大小,反演结果都比较准确,既得到了非常准确的背景值,异常体的范围和电阻率值也符合真实值,因此可以认为改进的量子遗传算法应用于基于子空间的二维MT 反演是成功的.
在反演过程中,当子空间为7个测点大小时,反演的模型参数要大大多于子空间为5 个测点大小时,所需要的种群个体数和遗传代数也大大增加,这样既增加了反演的时间,也增加了反演难度,同时效果并没有非常明显的提高.因此在下面实测资料的反演中我们采用5测点大小的子空间.
3.3 实测资料的反演本文选用的实测资料来自江西省鄱阳湖某地区的MT 实测数据.资料采集采用的是加拿大凤凰公司生产的V5-2000大地电磁测深仪器.
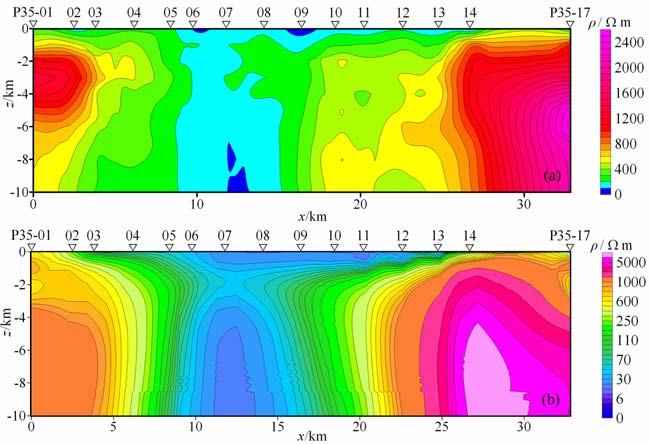
选取该区一条大地电磁测线(称之为G 测线)上的15个测点(测点号为1-14,17)的MT 资料做反演.为减少反演的难度,每个测点下方只划分一列网格,量子遗传算法各反演参数取值如下:种群个体数20,遗传代数100,变异概率0.01,产生“多胞胎"概率0.1,分辨率1.图 7a为改进量子遗传算法的反演结果,并与图 7b表示的常规反演结果对比,可见两者结果基本一致,说明算法具有一定的实用潜力.
|
图 7 改进量子遗传算法反演结果(a)和常规反演结果(b)对比 Fig. 7 Improved QGA inversion results (a) and traditional inversion results (b) |
本文在深入研究量子遗传算法基本原理的基础上,对常规量子遗传算法存在的不足进行了改进,并通过一维D 型和四层HK 型模型的反演验证了改进的有效性.利用滑动子空间的概念进行了常规量子遗传算法和改进量子遗传算法的二维MT 反演,无论模型试验还是实测数据,都得到了比较好的结果,证明了量子遗传算法在参数较多时仍具有较好的收敛性.但仍存在某些不足,如反演时间过长,在MATLAB7.0的环境下需10-20h, 反演时模型空间划分较简单.但总体上,本文的工作是成功的,希望能为以后二维乃至三维MT 的反演提供新的思路和方法.
| [1] | Smith J T, Booker J R. Rapid inversion of two-and three-dimensional magnetotelluric data. J. Geophys. Res. , 1991, 96(B3): 3905-3922. |
| [2] | Constable S C, Parker R L, Constable C G. Occam's inversion: A practical algorithm for generating smooth models from electromagnetic sounding data. Geophysics , 1987, 52(3): 289-300. DOI:10.1190/1.1442303 |
| [3] | DeGroot-Hedlin C, Constable S C. Occam's inversion to generate smooth, two-dimensional models from magnetotelluric data. Geophysics , 1990, 55(12): 1613-1624. DOI:10.1190/1.1442813 |
| [4] | Rodi W, Mackie R L. Nonlinear conjugate gradients algorithm for 2-D magnetotelluric inversion. Geophysics , 2001, 66(1): 174-187. DOI:10.1190/1.1444893 |
| [5] | 师学明, 王家映. 一维层状介质大地电磁模拟退火反演法. 地球科学-中国地质大学学报 , 1998, 23(5): 542–546. Shi X M, Wang J Y. One dimensional, magnetotelluric sounding inversion using simulated annealing. Earth Science-Journal of China University of Geosciences (in Chinese) , 1998, 23(5): 542-546. |
| [6] | 师学明, 王家映, 张胜业, 等. 多尺度逐次逼近遗传算法反演大地电磁资料. 地球物理学报 , 2000, 43(1): 122–130. Shi X M, Wang J Y, Zhang S Y, et al. Multiscale genetic algorithm and its application in magnetotelluric sounding data inversion. Chinese J. Geophys. (in Chinese) , 2000, 43(1): 122-130. |
| [7] | 娄素华, 吴耀武, 彭磊, 等. 量子进化算法在电力系统无功优化中的应用. 继电器 , 2005, 33(18): 30–35. Lou S H, Wu Y W, Peng L, et al. Application of quantum-inspired evolutionary algorithm in reactive power optimization. Relay (in Chinese) , 2005, 33(18): 30-35. |
| [8] | 伍亚萍, 陈海焱, 李大鹏, 等. 基于量子进化算法的配电网开关优化配置研究. 现代电力 , 2006, 23(3): 21–25. Wu Y P, Chen H Y, Li D P, et al. Switches optimal location scheme based on quantum evolution algorithm in distribution system. Modern Electric Power (in Chinese) , 2006, 23(3): 21-25. |
| [9] | 侯云鹤, 鲁丽娟, 熊信艮, 等. 量子进化算法在输电网扩展规划中的应用. 电网技术 , 2004, 28(17): 19–23. Hou Y H, Lu L J, Xiong X Y, et al. Application of quantum-inspired evolutionary algorithm in transmission network expansion planning. Power System Technology (in Chinese) , 2004, 28(17): 19-23. |
| [10] | 邵桂芳, 李祖枢, 刘恒, 等. 基于遗传量子的自适应图像分割算法. 计算机工程 , 2005, 31(22): 189–191. Shao G F, Li Z S, Liu H, et al. Adaptive image segmentation algorithm based on genetic quantum. Computer Engineering (in Chinese) , 2005, 31(22): 189-191. |
| [11] | 李映, 焦李成. 一种有效的基于并行量子进化算法的图像边缘检测方法. 信号处理 , 2003, 19(1): 69–74. Li Y, Jiao L C. An effective method of image edge detection based on parallel quantum evolutionary algorithm. Signal Processing (in Chinese) , 2003, 19(1): 69-74. |
| [12] | 杨俊安, 解光军, 庄镇泉, 等. 量子遗传算法及其在图像盲分离中的应用研究. 计算机辅助设计与图形学学报 , 2003, 15(7): 847–852. Yang J A, Xie G J, Zhuang Z Q, et al. Quantum genetic algorithm and its application to blind image separation. Journal of Computer Aided Design & Computer Graphics (in Chinese) , 2003, 15(7): 847-852. |
| [13] | 罗红明, 王家映, 朱培民, 等. 量子遗传算法在大地电磁反演中的应用. 地球物理学报 , 2009, 52(1): 260–267. Luo H M, Wang J Y, Zhu P M, et al. Quantum genetic algorithm and its application in magnetotelluric data inversion. Chinese J. Geophys. (in Chinese) , 2009, 52(1): 260-267. |
| [14] | 杨俊安, 庄镇泉. 多宇宙并行量子衍生遗传算法研究. 计算机工程与应用 , 2004, 40(20): 23–26. Yang J A, Zhuang Z Q. Research of multi-universe parallel quantum-inspired genetic algorithm. Computer Engineering and Applications (in Chinese) , 2004, 40(20): 23-26. |
| [15] | 杨俊安, 庄镇泉, 史亮. 多宇宙并行量子遗传算法. 电子学报 , 2004, 32(6): 923–928. Yang J A, Zhuang Z Q, Shi L. Multi-universe parallel quantum genetic algorithm. Acta Electronica Sinica (in Chinese) , 2004, 32(6): 923-928. |
| [16] | 郭海燕, 金炜东, 李丽, 等. 分组量子遗传算法及其应用. 西南科技大学学报(自然科学版) , 2004, 19(1): 18–21. Guo H Y, Jin W D, Li L, et al. Classified quantum genetic algorithm and its application. Journal of Southwest University of Science and Technology (in Chinese) , 2004, 19(1): 18-21. |
| [17] | 范晓志, 扈鹏. 基于改进量子遗传算法的有源噪声控制方法. 海军工程大学学报 , 2007, 19(1): 61–64. Fan X Z, Hu P. Active noise control method based on a new quantum genetic algorithm. Journal of Naval University of Engineering (in Chinese) , 2007, 19(1): 61-64. |
| [18] | 许波, 李智勇, 王永. 改进型量子遗传算法求解机器人联盟问题. 计算机工程与应用 , 2009, 45(4): 38–41. Xu B, Li Z Y, Wang Y. Improved quantum genetic algorithm for robot coalition problem. Computer Engineering and Applications (in Chinese) , 2009, 45(4): 38-41. |
| [19] | 李欣, 程春田, 曾筠. 基于改进量子遗传算法的过程神经元网络训练. 控制与决策 , 2009, 24(3): 347–351. Li X, Cheng C T, Zeng Y. Training of process neural networks based on improved quantum genetic algorithm. Control and Decision (in Chinese) , 2009, 24(3): 347-351. |
| [20] | 高颖慧, 沈振康. 角度编码染色体量子遗传算法. 计算机工程与科学 , 2009, 31(3): 75–79. Gao Y H, Shen Z K. An angle-coding chromosome quantum genetic algorithm. Computer Engineering & Science (in Chinese) , 2009, 31(3): 75-79. |
| [21] | Kennett B L N, Williamson P R. Subspace methods for large-scale nonlinear inversion. In: Marhemmical Geophysics: A Survey of Recent Developments in Seismology and Geodynamics, 1988. 139-154 http://cn.bing.com/academic/profile?id=170642317&encoded=0&v=paper_preview&mkt=zh-cn |
| [22] | Oldenburg D W, McGillivray P R, Ellis R G. Generalized subspace methods for large-scale inverse problems. Geophys.J. Int. , 1993, 114(1): 12-20. |
 2011, Vol. 54
2011, Vol. 54





