探地雷达(Ground-penetratingradar, 简称为GPR)以其高分辨率、高效和无损等优点,成为工程勘察和考古中一种有效的浅层地球物理探测方法[1-4].多数探地雷达采用非屏蔽天线,其发射的电磁波会在空中传播.空气中衰减非常小,使得地面以上物体如铁块、电线、铁丝网、建筑物等产生的反射会叠加在有效反射信号上,其能量相对较强,甚至有可能掩盖有效信号.去除这种反射干扰是探地雷达勘探工作需要解决的重要问题.国内学者大多进行干扰总结研究,优化采集过程和尝试一些数据处理[5,6],国外学者偏重于研究识别和压制方法[7-12],本文则重点研究和分析干扰的传播特征,试图寻找一种合适的干扰压制方法.
利用电磁波时域有限差分(FDTD)进行正演模拟计算[13,14],可研究不同干扰源的探地雷达响应特征.任意干扰源都可认为是由无穷多个点源组成,同时如果干扰源很小或离测线的距离远大于其尺寸时,就可近似认为是点源干扰.故进行点源抽象模型的模拟研究就很有必要.此外,实际探测时,还会经常遇到像电线、电网等可认为是线源和面源的干扰源,本文还进行了线源和面源两种干扰源抽象模型的正演模拟研究.
利用射线理论推导出的地面以上物体反射干扰波时距曲线表达式进行特征分析,具有计算简便、结果直观、易于进行多影响因素识别以及多曲线叠加显示的优点,可以为反射干扰时距曲线特征的提取,为干扰的有效识别和去除,提供有用的基础和方法.
2 FDTD 方法参数设置探地雷达电磁波的传播特征可用麦克斯韦旋度方程组来描述:
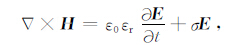
|
(2) |
式中E表示电场强度,单位为V/m;H表示磁场强度,单位为A/m;ε0 表示真空介电常数,单位为F/m,εr 表示相对介电常数,ε=ε0εr 表示介质的介电常数;μ0 表示真空磁导率,单位为H/m,μr 表示相对磁导率,μ=μrμ0 表示介质的磁导率;σ 表示电导率,单位为 s/m;t表示时间,单位为s.设网格单元在x,y,z三个坐标轴方向的长度分别为dx,dy,dz,时间增量为dt,对式(1)(2)应用下面的中心差分近似:
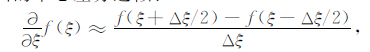
|
(3) |
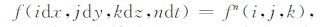
|
(4) |
即可得到麦克斯韦旋度方程组在直角坐标系中的FDTD 离散形式.限于篇幅只列出电场强度y方向分量Ey的差分方程:
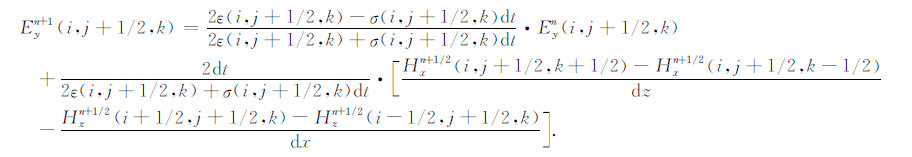
|
(5) |
本文正演时的信号源为电场y方向水平偶极子,信号脉冲为雷克子波,最大输入电压为500 V,中心频率为900 MHz, 采样间隔dt=0.0625ns, 空间模型dx=dy=dz=0.04m, 满足Courant稳定性条件[13],延迟时间为2ns, 记录长度为50ns, 模型外形尺寸为129×129×129 个网格,即5.12 m×5.12m×5.12m.程序使用Mur吸收边界条件,采用C 语言实现.
3 模拟结果目前探地雷达应用领域中的绝大多数介质,其磁导率的影响可暂不考虑[15],故本文模型中介质的相对磁导率皆为1.以两层模型(上层为空气层,下层为半无限空间)和相应的干扰源组成最终模型,进行正演模拟研究.空气层电性参数为εr=1,σ=0 s/m; 下层介质的电性参数为εr=4,σ=0 s/m, 可近似模拟干砂(土)、花岗岩、火山凝灰岩等[15-17].所设计的干扰源介质主要考虑金属介质,以及其他还可能碰到的干扰源,如电线柱、建筑物等.干扰源介质的电性参数为εr=36,σ=10 s/m.
3.1 点源干扰介质正演模拟结果图 1所示模型中点源干扰的尺寸为0.08 m×0.36m×0.36m, 中心坐标为(2.52,0,-0.18).将点源干扰模拟结果和无干扰的两层模型模拟结果进行对比(图 2),发现点源干扰的存在会产生明显的反射干扰波,且以光速传播.对图 1 所示模型,通过修改输入子波的中心频率和修改点源干扰源的大小而不改变其位置,可研究探地雷达的发射频率、干扰源尺寸与干扰影响程度的关系.
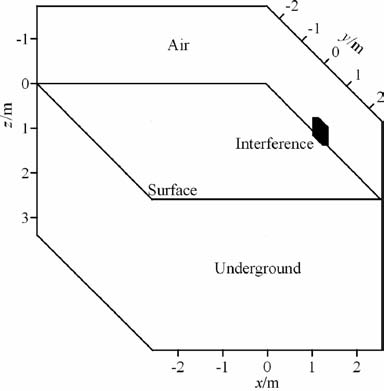
|
图 1 带点源干扰的两层模型(图中黑块为干扰源) Fig. 1 Two layers model with point source interference(Shown in the black block) |

|
图 2 不同时刻有无点源干扰Ey分量对比(a、c)无干扰两层模型正演结果;(b、d)图 1点源干扰模型正演结果;(a、b)y=0m 的xz面;(c、d)z=0m 的xy面. Fig. 2 Ey component comparison between with and without interference in different times(a、c) The for ward results of two layers model without interference; (b、d) The for ward results with points ource interference as show inFig.1;(a、b) Thexzplaneaty=0m; (c、d) Thexy plan eatz=0m. |
本文设计了三种中心频率,分别为500 MHz、900 Mhz、1200 MHz, 同时也设计了三种尺寸的点源干扰源,分别为0.08m×0.36m×0.36m, 0.08m×0.16m×0.16m, 0.08m×0.08m×0.08m.图 3为在20ns时的正演结果(y=0 m 处的xz面),图中频率越高,尺寸越大,干扰影响越明显,当频率较低、且干扰源尺寸较小时(图 3c),干扰源几乎不产生干扰.
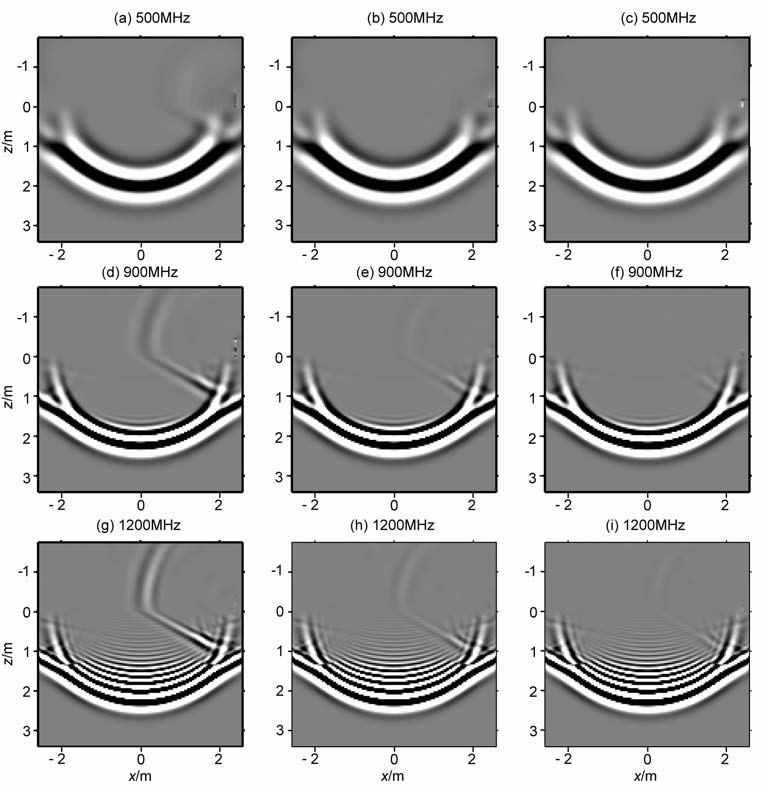
|
图 3 t=20ns时不同频率、不同尺寸大小点源干扰对比取y=0m 处的xz面做对比;(a、b、c)中心频率为500 MHz; (d、e、f)中心频率为900 MHz; (g、h、i)中心频率为1200 MHz; (a、d、g)模型中干扰源尺寸为0.08m×0.36m×0.36m; (b、e、h)模型中干扰源尺寸为0.08m×0.16m×0.16m; (c、f、i)模型中干扰源尺寸为0.08m×0.08m×0.08m. Fig. 3 Comparison between different frequency and size of points ource interference whent=20ns Take thexz plan eaty=0m to do comparison. The center frequency of (a、b、c) is500MHz, the center frequency of(d、e、f)is900MHz, the center frequency of(g、h、i)is1200 MHz. The interference size of(a、d、g)is0.08m×0.36m×0.36m, the interference sizeof(b、e、h)is0.08m×0.16m×0.16m, theinterferencesizeof(c、f、i)is0.08m×0.08m×0.08m. |
图 4所示模型中线源干扰尺寸大小为5.12m×0.08m×0.08m, 离地表1.16m.正演输出结果(图5)表明,线源干扰的存在会产生反射干扰.16ns时在地表xy面(图 5c)电磁波波前发生变化,向x方向(平行测线方向)拉伸.说明当存在线源干扰,且激励源在线源正下方时,不同方向的干扰情况不一样,平行线源方向的干扰波会快于垂直线源方向.
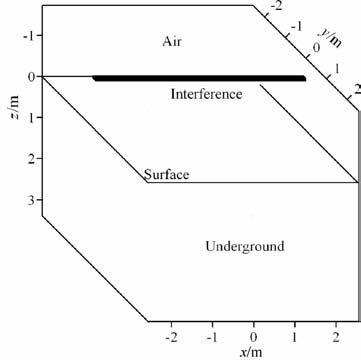
|
图 4 带线源干扰的两层模型(图中黑条为干扰源) Fig. 4 Two layers model with line source interference (Shown in black bar is the source of interference) |

|
图 5 不同时刻线源干扰Ey分量 (a)y=0m 的xz面;(b)x=0m 的yz面;(c)z=0m 的xy面. Fig. 5 Ey component of line source interference in different times (a)xz plane aty=0m; (b)yz plane atx=0m; (c)xy plane atz=0m. |
图 6模型中面源干扰尺寸为0.08m×2.56m×1.72m, 模拟结果见图 7.该模型与点源干扰模型正演结果(图 2b、图 2d)对比,两者形态接近,但面源干扰的能量要强.
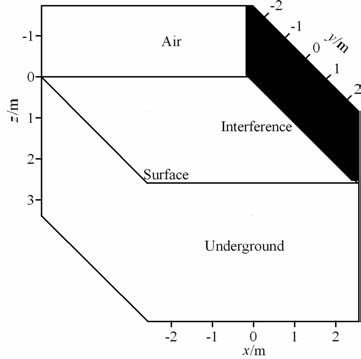
|
图 6 带面源干扰的两层模型(图中黑块为干扰源) Fig. 6 Two layers model with plane source interference(Shown in black block is the source of interference) |

|
图 7 不同时刻面源干扰Ey分量(a)y=0m 的xz面;(b)x=0m 的yz面;(c)z=0m 的xy面. Fig. 7 Ey component of plane source interference in different times (a)xz plane aty=0m; (b)yz plane atx=0m; (c)xy plane atz=0m. |
设计了l条x测线和y测线(见图 8),且以测线交点o为原点,建立直角坐标系.则x测线方程为y=0m,z=0m;y测线方程为x=0m,z=0m.利用图 8所示的无干扰两层模型、图 1的点源模型、图4的线源模型、图 6 的面源模型进行不同探测方式下的正演模拟对比研究.此时测线和干扰源的位置关系为:点源在x测线上,不在y测线上;线源平行x测线,垂直y测线,且在原点o的正上方;面源和x测线垂直相交,和y测线平行.

|
图 8 x和y剖面测线布置示意图(图中虚线,x、y测线) Fig. 8 layout diagram ofx andy measured lines (Dotted lines,x,y survey lines inter sectat the origino) |
宽角法测量方式要求一个天线固定在某一点不动,而另一个天线沿测线移动.将固定的天线位置设为原点o,另一个天线沿测线移动.通过与无干扰时的结果(图 9(a、b))对比,可发现对于点源,x测线的干扰时距曲线表现为斜线(图 9c),y测线表现为曲线(图 9d).对于线源,x、y测线上的干扰时距曲线皆表现为曲线(图 9(e、f)),且顶点都在0m 处,x测线的干扰初至时间除0m 处,皆早于y测线.对于面源,x测线上干扰时距曲线表现为斜线(图 9g),y测线表现为曲线(图 9h),与点源干扰比较相似,但其能量较强.图 9中的干扰时距曲线主要表现为斜线和曲线,而没有水平线.
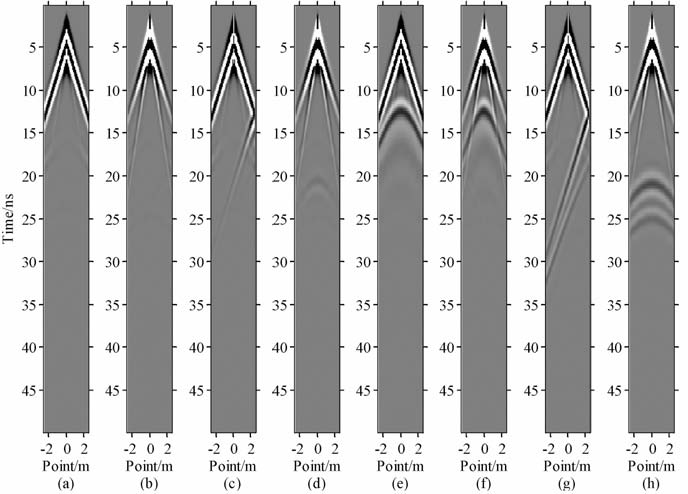
|
图 9 宽角法测量横轴坐标为移动天线在测线上的坐标. (a)无干扰x测线;(b)无干扰y测线;(c)点源干扰x测线;(d)点源干扰y测线;(e)线源干扰x测线;(f)线源干扰y测线;(g)面源干扰x测线;(h)面源干扰y测线. Fig. 9 WARR measurement profiles Horizontal coordinates for the mobile antenna coordinates in the measuring line. (a)Without interference &x measured line; (b)Without interference&y measured line; (c)Point source interference&x measured line; (d)Point source interference&y measured line; (e)Line source interference&x measured line; (f)Line source interference&y measured line; (g)Plane source interference&x measured line; (h)Plane source interference&y measured line. |
共中心点法测量方式要求发射天线和接收天线以相同固定步距沿测线分别向两端同时移动,或从两边向中点同时移动,两个天线的中点位置保持不变,可将其设在原点o.通过与无干扰时的结果(图10(a、b))对比,可发现对于点源,x测线上干扰时距曲线表现为水平线(图 10c),y测线表现为曲线(图10d).对于线源,x测线和y测线上的干扰时距曲线皆表现为曲线(图 10(e、f)),且顶点都在0 m 处,x测线干扰初至时间除0m 处外皆晚于y测线.面源与点源干扰相似,但能量要强.
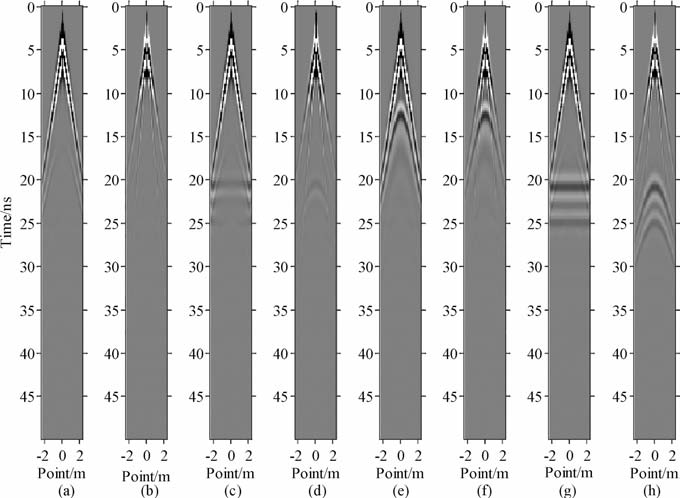
|
图 10 共中心点法测量横轴坐标为发射天线在测线上的坐标. (a)无干扰x测线;(b)无干扰y测线;(c)点源干扰x测线;(d)点源干扰y测线;(e)线源干扰x测线;(f)线源干扰y测线;(g)面源干扰x测线;(h)面源干扰y测线. Fig. 10 CMP measurement profiles Horizontal coordinates for the transmitter antenna in the coordinate measuring line. (a)Without interference&x measured line; (b)Without interference&y measured line; (c)Point source interference&x measured line; (d)Point source interference&y measured line; (e)Line source interference&x measured line; (f)Line source interference&y measured line; (g)Plane source interference&x measured line; (h)Plane source interference&y measured line. |
剖面法是发射天线和接收天线以固定间距沿测线同步移动的一种测量方式.图 11是模拟自激自收时的情况.通过与无干扰时的结果(图 11(a、b))对比,可发现对于点源,x测线上干扰时距曲线表现为斜线(图 11c),y测线表现为曲线(图 11d).对于线源,x测线上干扰时距曲线表现为水平线(图 11e),而y测线表现为曲线(图 11f).对于面源,x测线上干扰时距曲线表现为斜线(图 11g),y测线表现为水平线(图 11h).

|
图 11 自激自收时剖面法测量剖面横轴坐标为发射天线在测线上的坐标. (a)无干扰x测线;(b)无干扰y测线;(c)点源干扰x测线;(d)点源干扰y测线;(e)线源干扰x测线;(f)线源干扰y测线;(g)面源干扰x测线;(h)面源干扰y测线. Fig. 11 Profile measurement profiles while self-excited and self-closing Horizontal coordinates for the transmitter antennain the coordinate measuring line. (a)Without interference&x measured line; (b)Without interference&y measured line; (c)Point source interference&x measured line; (d)Point source interference&y measured line; (e)Line source interference&x measured line; (f)Line source interference&y measured line; (g)Plane source interference&x measured line; (h)Plane source interference&y measured line. |
FDTD正演模拟结果表明,点源在不在测线上对干扰曲线的形态有很大的影响;采用剖面法测量时(图 11),线源或面源平行测线和垂直测线时的干扰曲线不一样;不同的干扰源可能产生相类似的时距曲线.模拟结果还表明在剖面法测量时,可能会出现水平线,而这种干扰波是很难去除的,故在野外采集数据时,应注意避开这种情况.本节将针对上述地面以上物体的反射干扰特征,结合射线理论推导的一般表达式,进行多个参数影响下的干扰时距曲线时空特征分析.
当探地雷达发射频率很高,位移电流占主导地位,电磁波衰减很小时,就可以应用射线理论进行近似计算[18,19].地面以上物体的反射干扰波主要是在空气中传播,满足射线理论近似计算的条件,可以用射线理论推导出相应测量方式下的干扰时距曲线表达式,并进行多影响因素识别和多曲线叠加显示下的干扰特征分析,而这些优点用FDTD方法则难以达到.若设电磁波在均匀介质中传播,且速度为v ,初至时间为t.并设点源坐标为(a,b,c),其到原点的距离为
以固定不动的天线所在点为坐标原点,以测线方向为x轴,则可设两个天线的坐标分别为(0,0,0)和(x,0,0).式(6)、(7)、(8)分别为点源、线源、面源干扰源的时距曲线表达式.

|
(6) |
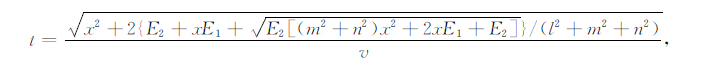
|
(7) |
式中
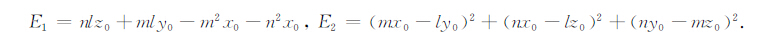
|
如果干扰源为面源,当两个天线在面源的两侧或有一个在面源时,t=x/v ,但这时是透射而非反射.野外地面测量时,多是两个天线在面源的同侧,这时有
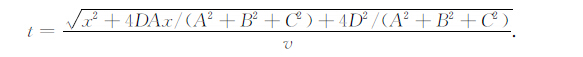
|
(8) |
坐标系建立时以两天线的中点为原点,以测线为x轴,则可设发射天线坐标为(x,0,0),接收天线坐标为
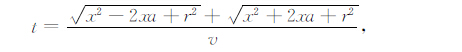
|
(9) |
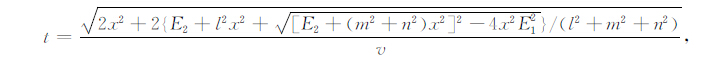
|
(10) |
式中

|
如果干扰源为面源,当两个天线在面源的两侧或有一个在面源时,t=2x/v ,但这时是透射而非反射.野外地面测量时,多是两个天线在面源的同侧,这时有
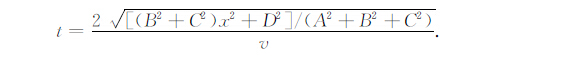
|
(11) |
坐标系建立时以发射天线所在测线为x轴,天线距为d,且两天线的连线与x轴夹角为θ,θ∈[0,2π),则可设发射天线坐标为(x,0,0),接收天线坐标为(dcosθ+x,dsinθ,0).式(12)、(13)、(14)分别为点源、线源、面源干扰源的时距曲线表达式.
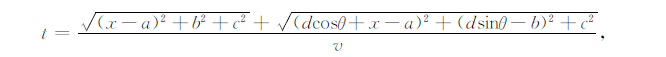
|
(12) |

|
(13) |
式中
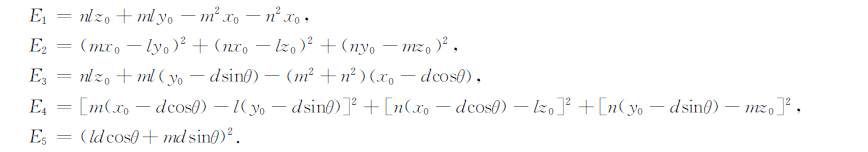
|
如果干扰源为面源,当两个天线在面源的两侧或有一个在面源时,t=d/v ,但这时是透射而非反射.野外地面测量时,多是两个天线在面源的同侧,这时有
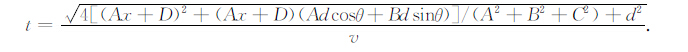
|
(14) |
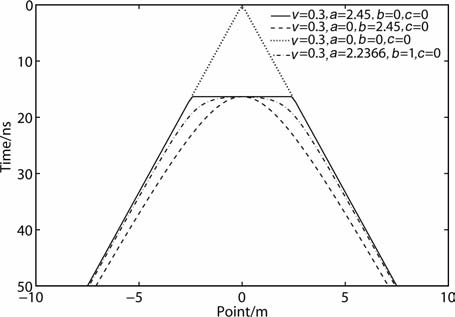
由式(6)可知,采用宽角法测量,点源干扰表现为两组斜率相反的斜线(点源在测线上,图 12实线)或双曲线(点源不在测线上,图 12虚线),且顶点在x-t剖面上坐标为(a,[r+(b2+c2)1/2]/v ).
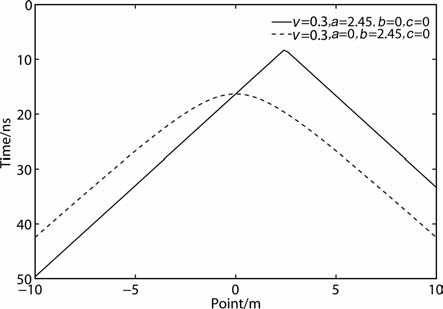
|
图 12 宽角法测量(v :速度,a、b、c:干扰位置) Fig. 12 WARR(v :velocity,a、b、c:interference location) |
由式(9)可知,采用共中心点法测量,点源在测线上时,若点源在测线中点为两组斜率相反的斜线(图 13中点线),不在中点则为两组斜率相反的斜线夹水平线(图 13中实线);点源不在测线上时,若a=0为双曲线(图 13虚线),若a≠0则为四次曲线(图 13点虚线).且在x=0,即自激自收时,干扰到达时间最早为2r/v .
|
图 13 共中心点法测量 Fig. 13 CMP |
由式(12)知,采用剖面法测量,若d=0,点源在测线上为两组斜率相反的斜线(图 14中i线),点源不在测线上为双曲线(图 14中v线),顶点在x-t剖面上坐标为(a,2(b2 +c2)1/2/v ).当r2 =a2,d≠0,sinθ=0时为两组斜率相反的斜线夹水平线(图 14中ii线);当r2 =a2,dsinθ≠0,或r2 ≠a2,dsinθ=b,c=0为双曲线(图 14中iii线);当r2 ≠a2,(dsinθ-b)2 +c2≠0为四次曲线(图 14中iv线).综上所述,通过干扰曲线最早到达时间坐标,就能获得干扰源位置信息.
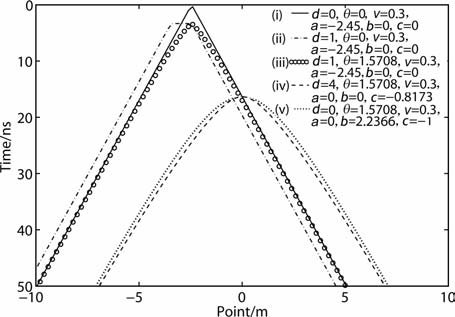
|
图 14 剖面法测量(d:天线间距,θ:两天线连线与x轴夹角) Fig. 14 Profile measurement (d:antenna space,θ:the angle between the antenna connection and thex-axis) |
假设线源干扰平行地表(如输电线),且位于原点正上方,即n=0,x0=y0=0;z0≠0,设γ 为线源正方向和测线(x轴)的夹角,当sinγ=0,即线源和测线平行时,干扰曲线为水平线(图 15a中γ=0),当sinγ≠0 时干扰曲线为曲线,在x=dsin(θ -γ)/(2sinγ)处,干扰到达时间最早为(d2+4z02)1/2/v ;当d=0,即自激自收时(图 15a),x=0即位于线源正下方时,干扰到达时间最早为2z0/v ,而sin2γ值越大干扰到达时间越晚;当d≠0,γ=π/2,θ=0,线源在地表的投影线在两个天线之间时,干扰曲线会接近水平线(图 15b).
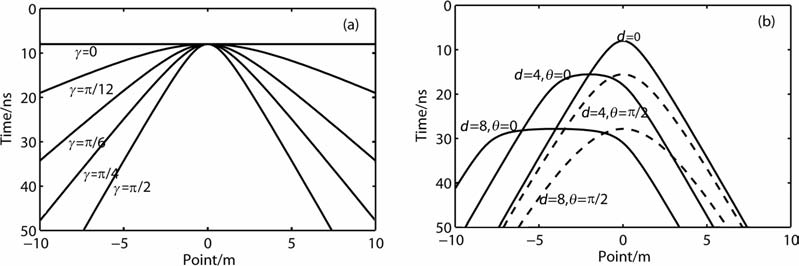
|
图 15 线源与测线夹角以及天线距对干扰曲线的影响(a)天线距d=0时,不同夹角γ 的影响;(b)线源与测线垂直,即γ=π/2时,不同天线距d以及两天线连线与x轴夹角θ 的影响. Fig. 15 The impac to fangle between line source and the measurement line and antenna distance(a) The impact of different anglesγ whend=0;(b) The impact of different antenna spaces and anglesθwhenγ=π/2. |
设面源干扰垂直地表(如墙),即C=0,且原点到面源的距离大于0,λ 为面源与测线的夹角,并只考虑反射的情况.当sinλ=0,即面源和测线平行时,干扰曲线为水平线(图 16a中λ=0);当d=0,即自激自收时(图 16a),sinλ 的值越大,干扰曲线斜率越大.当d≠0,θ=π,λ=π/2时,干扰曲线仍为斜线,只是干扰波到达时间t与d=0 时相差±d/v (图 16b中实线),当d≠0,θ=π/2,λ=π/2时,干扰曲线变成双曲线的一部分(图 16b中虚线).
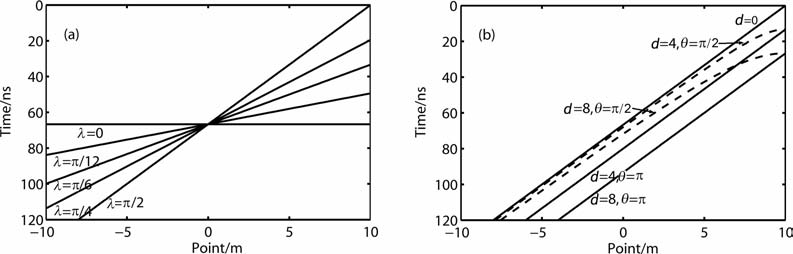
|
图 16 面源与测线夹角以及天线距对干扰曲线的影响(a)天线距d=0时,不同夹角λ 的影响;(b)面源与测线垂直即λ=π/2时,天线距d以及两天线连线与x轴夹角θ 的影响. Fig. 16 The impact of angle between plane source and the measurement line and antenna distance(a) The impact of different anglesλ whend=0;(b) The impact of different antenna spaces and anglesθwhenλ=π/2. |
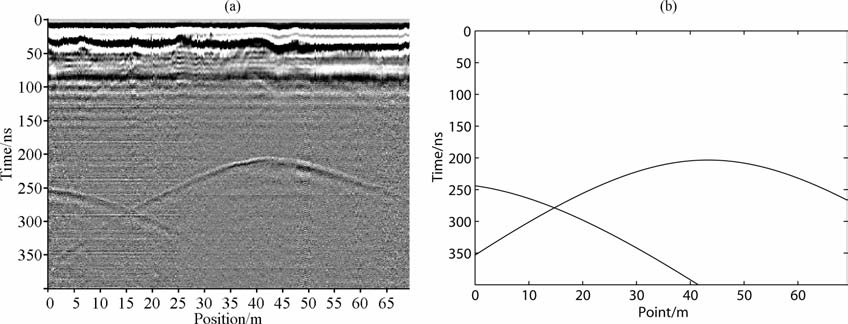
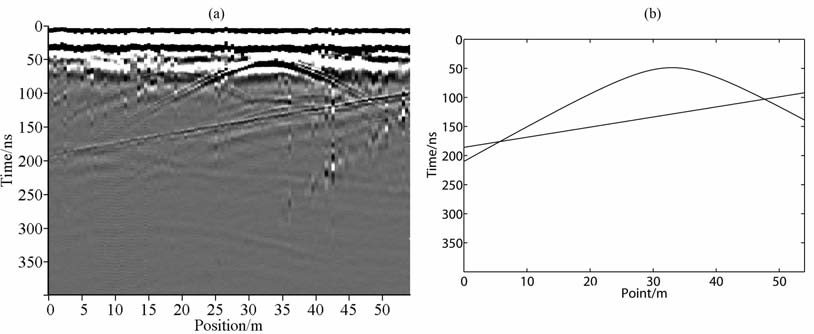
图 17地面有两根电线柱,由于它们的尺寸远小于它们到测线的距离,故可看成点源,图 17b为根据式(12)计算的结果(两个点源的参数分别为a=43.8,b=30.5,c=0和a=-6,b=36,c=0),与实测剖面(图 17a)中相应位置的两条曲线同相轴一致.图 18上空有一电线(基本平行地表),可看成线源;地面上还存有一建筑,可看成面源,图 18b为根据式(13)(线源参数l=0.4,m=1,n=0,x0 =33.5,y0 =0,z0 =7.3)和式(14)(面源参数A= 0.27,B=1,C=0,D=-29)计算的结果,与实测剖面(图 18a)中相应位置的曲线、斜线同相轴一致.
|
图 17 点源干扰 (a)实测剖面;(b)计算的剖面. Fig. 17 Point source interference (a) The measured profile; (b) The calculated profile. |
|
图 18 线源和面源干扰 (a)实测剖面;(b)计算剖面,曲线为线源干扰,斜线为面源干扰. Fig. 18 Line and plane source interference (a) The measured profile; (b) The profile calculated according to equation (13)and(14),Curve for the line source interference, slash for the plane source interference. |
本文研究结果表明,空中及地面存在的干扰源会产生明显的反射干扰,这种干扰主要受干扰源类型及干扰源与测线的位置关系影响.若探地雷达天线没有屏蔽,则发射频率越高,干扰源尺寸越大,干扰影响越明显.
利用射线理论推导出了三种测量方式下三种类型干扰源的一般时距曲线表达式,其计算结果表明多种测量方式结合有利于对干扰的识别和去除.特别当采用剖面法测量,而干扰时距曲线表现为水平线时,只根据一张剖面无法计算电磁波速度,进而有效判断其是干扰波还是有效波.这时采用宽角法辅助测量,就可以通过计算电磁波速度以提供相关的干扰源信息,从而在剖面法测量的雷达数据中识别和去除干扰.
根据地面以上物体计算出干扰的时距曲线,有助于指导野外操作人员设计合理的探测方式以及测线布置,从而优化采集过程,减少室内处理的难度.例如采用剖面法测量时,若测线和线源或面源干扰源平行,可能会出现水平线型的干扰,野外测线布置时应尽量避免这种情况.
不同干扰源与测线处于某些特定位置关系时,可能会产生相同或相似的干扰时距曲线.进行干扰识别和去除数据处理时,需要引起注意.地面以上物体反射干扰特征分析的根本目的在于识别和去除这种干扰.因此我们认为可按下述流程进行今后的研究:先依据射线理论的表达式,进行干扰的自动识别以及干扰源的有效判断,接着研究去除某一特定类型的反射干扰,最后研究能去除任意类型干扰的数据处理技术.
| [1] | Negri S, Leucci G, Mazzone F. High resolution 3D ERT to help GPR data interpretation for researching archaeological items in a geologically complex subsurface. Journal of Applied Geophysics , 2008, 65(3-4): 111-120. DOI:10.1016/j.jappgeo.2008.06.004 |
| [2] | Francese R G, Finzi E, Morelli G. 3-D high-resolution multi-channel radar investigation of a Roman village in Northern Italy. Journal of Applied Geophysics , 2009, 67(1): 44-51. DOI:10.1016/j.jappgeo.2008.09.004 |
| [3] | Slob E, Sato M, Olhoeft G. Surface and borehole ground-penetrating-radar developments. Geophysics , 2010, 75(5): A103-A120. |
| [4] | 卢成明, 秦臻, 朱海龙, 等. 探地雷达检测公路结构层隐含裂缝实用方法研究. 地球物理学报 , 2007, 50(5): 1558–1568. Lu C M, Qin Z, Zhu H L, et al. Practical methods for detection of concealed cracks in highway pavement using ground penetration radar data. Chinese J. Geophys. (in Chinese) , 2007, 50(5): 1558-1568. |
| [5] | 杨峰, 高云泽, 康文献. 地质雷达剖面高压线干扰的识别与去除. 工程地球物理学报 , 2005, 2(4): 276–281. Yang F, Gao Y Z, Kang W X. Identification and removing of the city high-voltage line interference from geological radar profile. Chinese Journal of Engineering Geophysics (in Chinese) , 2005, 2(4): 276-281. |
| [6] | 许新刚, 李党民, 周杰. 地质雷达探测中干扰波的识别及处理对策. 工程地球物理学报 , 2006, 3(2): 114–118. Xu X G, Li D M, Zhou J. Identifying interferential wave in GPR and its countermeasure. Chinese Journal of Engineering Geophysics (in Chinese) , 2006, 3(2): 114-118. DOI:10.1088/1742-2132/3/2/002 |
| [7] | Bano M, Pivot F, Marthelot J M. Modelling and filtering of surface scattering in ground-penetrating radar waves. First Break , 1999, 17(6): 215-222. DOI:10.1046/j.1365-2397.1999.00703.x |
| [8] | Basile V, Carrozzo M T, Negri S, et al. A ground-penetrating radar survey for archaeological investigations in an urban area (Lecce, Italy). Journal of Applied Geophysics , 2000, 44(1): 15-32. DOI:10.1016/S0926-9851(99)00070-1 |
| [9] | van der Kruk J, Slob E C. The influence of the soil on reflections from above surface objects in GPR data. 8th International Conference on Ground Penetrating Radar (GPR 2000), GPR 2000: Proceedings of the Eighth International Conference on Ground Penetrating Radar , 2000: 453-458. |
| [10] | van der Kruk J, Slob E C. Reduction of reflections from above surface objects in GPR data. Journal of Applied Geophysics , 2004, 55(3-4): 271-278. DOI:10.1016/j.jappgeo.2004.02.002 |
| [11] | Nuzzo L, Quarta T. Improvement in GPR coherent noise attenuation usingτ-p and wavelet transforms. Geophysics , 2004, 69(3): 789-802. DOI:10.1190/1.1759465 |
| [12] | Nuzzo L. Identification and removal of above-ground spurious signals in GPR archaeological prospecting. 27th General Meeting of the European-Geophysical-Society, Archaeological Prospection , 2005: 93-103. |
| [13] | 葛德彪, 闫玉波. 电磁波时域有限差分方法(第二版). 西安: 西安电子科技大学出版社, 2005 . Ge D B, Yan Y B. Finite-difference time-domain method for electromagnetic waves (second edition) (in Chinese). Xi'an: Xidian University Press, 2005 . |
| [14] | Holt J J. Finite difference time domain modeling of dispersion from heterogeneous ground properties in ground penetrating radar . Department of Geological Sciences, The Ohio State University, 2004 |
| [15] | 曾昭发, 刘四新, 王者江, 等. 探地雷达方法原理及应用. 北京: 科学出版社, 2006 . Zeng Z F, Liu S X, Wang Z J, et al. Principles and Applications of GPR method (in Chinese). Beijing: Science Press, 2006 . |
| [16] | 曾昭发, 刘四新, 冯晅. 探地雷达原理与应用. 北京: 电子工业出版社, 2010 . |
| [17] | 孙建国. 岩石物理学基础. 北京: 地质出版社, 2006 . Sun J G. Rock Physics Basis (in Chinese). Beijing: Geological Publishing House, 2006 . |
| [18] | Cai J, McMechan G A. Ray-based synthesis of bistatic ground-penetrating radar profiles. Geophysics , 1995, 60(1): 87-96. DOI:10.1190/1.1443766 |
| [19] | Cai J, McMechan G A. 2-D ray-based tomography for velocity, layer shape, and attenuation from GPR data. Geophysics , 1999, 64(5): 1579-1593. DOI:10.1190/1.1444662 |
 2011, Vol. 54
2011, Vol. 54


