对于了解地震断层破裂过程来说,地震波辐射能ES 和标量地震矩M0 是两个重要的震源物理参数.前者为一个动态量,给出了断层破裂过程中地震波辐射能量的大小;后者则同断层破裂尺度和滑移大小相关.ES 与M0 的比值乘以剪切模量μ 称为视应力af.af 的物理意义是单位面积单位滑动位移下地震波辐射能的大小.对于一个圆盘断层模型,通过求解断层的动态破裂过程,远场S-波辐射能量可表达为[1,2]:
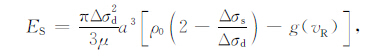
|
(1) |
其中Δσs,Δσd 和vR 分别是静态应力降、动态应力降和破裂速度;a为圆盘的半径;μ 为剪切模量;g(vR)是一个与断层面上滑移速率相关的无量纲的参数[1],表达了断层动态破裂过程中破裂能(表面能)所占份额: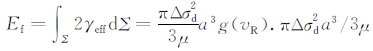
比较图 1a和1b,M-模型得到的断层面上的平均滑移速率和平均滑动位移大于D-模型的.而将M-模型、D-模型同图 1c的Brune[4]模型进行比较可知,Brune给出的平均滑移速率结果远小于M-模型和D-模型的值,但是平均滑动位移的值相差不大.Brune模型在观测地震学中广泛用于对震源参数的求解,但所得到的断层几何尺度,如圆盘断层模型的半径,往往大于由M-模型或D-模型所获得的结果.
实际的断层动态破裂过程是非常复杂的.动态滑移过程可能对应了动摩擦应力上调、下调或完全应力降.因此对应不同的模型来讲,能量的辐射值或视应力af 相差较大.因此,对能量而言,我们需要在适当的破裂模型下给出统一的表达式,以便用于对能量大小的界定和对近场强地面运动的约束.
Brune和Thatcher[6]在对1999 年集集地震的讨论中指出,远场视应力与近场视应力相差几倍.近场和远场能量之比高达10,从而推测大部份能量未能辐射至远场,可能在断层附近耗散.其物理机制则同逆冲断层的空间几何不对称相关,断层上盘的能量被陷于上盘,造成上盘的剧烈震动[6].
McGarr和Fletcher[7]则基于Madariaga[1]的远场地震波辐射能表达式(1),给出了当破裂速度为0.6β、0.75β 和0.9β 时,得到远场与近场地震波辐射能量比为0.11、0.22和0.35.也就是说,有多于2/3的能量以永久形变的方式集中在近场.由于Madariaga[1]是把摩擦应力σd 当做最终摩擦应力σf, 只考虑应力上调的情况,而且g(vR)表达式复杂,不可连续求解,所以McGarr和Fletcher[7]得到的结果也存在明显的局限性.
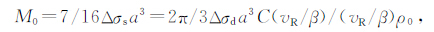
|
那么有
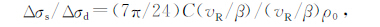
|
其中,ρ0=1.52,C(vR/β)为Kostrov函数,在vR/β=0.6,0.75和0.9时,C(vR/β)分别等于0.59、0.71和0.82,所以C(vR/β)/(vR/β)永远小于1.假设a为圆盘模型的半径,将一个圆盘分成五个同心圆环,每一个圆环的宽度为a/5.在vR/β=0.9的情况下,M-模型和D-模型的每一个圆环所对应的平均滑动速率和滑动位移函数由图 1a和1b所示.图 1c为由Brune[4]模型给出的平均滑动位移速率和滑动位移函数.
|
图 1 (a)M-模型每一个圆环所对应的平均滑动速率和滑动位移函数.v 是初始破裂速度,a是最终破裂半径,vR 是破裂速度,t是时间,Δ$\dot{u}$0是初始滑移速率,$\Delta \dot u$ 是滑移速率.取vR/β=0.9,在时间ts(r)之前图形是自相似的,ts(r)表示P 波停止相位的到时函数.曲线的拐点就是其到时,预示着断层开始愈合;(b)D-模型每一个圆环所对应的平均滑动速率和滑动位移函数,在时间ts =0.82a/v 之前图形是自相似的,之后断层开始减速,直到th =1.22a/v 时整个断层滑动愈合.但是,在r=0.95a时破裂前缘存在延迟;(c)由Brune[4]模型给出的平均滑动位移速率和滑动位移函数 Fig. 1 (a)Plots of the relative slip velocity and slip, for the M-model.v isinitialrupturevelocity,aisfinal fault radius,vR is rupture velocity,tistime, $\Delta \dot u$0 is in itial particle velocity, $\Delta \dot u$ isparticle velocity.vR/β=0.9,at five different radii. The motionat each radiusis self-similar untilts(r),which is the arrival time of the P-wave stopping phase. The corners in the slip velocity mark this arrival time; (b)Plots of the relative slip velocity and slip, for the D-model at five different radii. The motion at each radiusis self-similar untilts =0.82a/v ,whenthe fault begins to decelerate. The slipheals over the entire fault surfac eatth =1.22a/v .Note the delay of the rupture front arrival forr=0.95a; (c)Plots of the relative slip velocity and slip, for the Brune-model[4] |
本文主要基于断层带模型(FaultZone Model)中常用的简单滑移弱化准则,在考虑破裂能的情况下,推导出远场S-波辐射能量公式,并同M-模型和D-模型进行了对比.结合近断层的断层运动所做的功,将其运用到近场地震波辐射能量的求解过程中,我们得到了近场能量解并同McGarr和Fletcher[7]得到的值进行比较.利用近场地震波辐射能与加权滑动速率的关系对汶川地震和集集地震的实例做近场平均滑动速率的估计.从而,对强地面运动的研究过程给予速度参数约束.
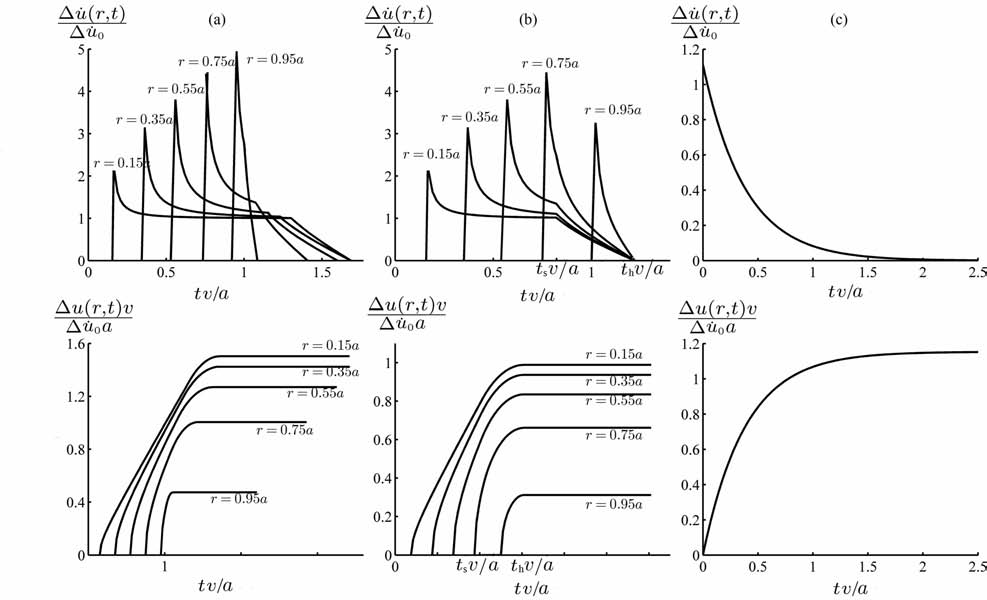
2 模型S-波能量辐射方程可表达为[8]:
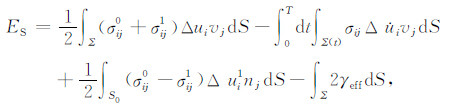
|
(2) |
其中,σij0和σij1分别为初始应力和终止应力,σij为瞬态应力,$\Delta {\dot u_i}$是滑动速率,Δui为滑动位移,Δui1是最终滑动位移,Σ 为断层面面积,T为滑动过程所经历的时间,S0 是包含断层面的一个封闭曲面,vj和nj为作用于断层面Σ 和S0 的单位方向矢量,γeff 为有效表面能.如果S0 远离震源区,即封闭曲面的半径远大于断层的特征尺度,r$\gg $L,则公式(2)中右侧第三项可以忽略.分部积分后则有:
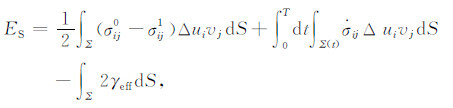
|
(3) |
公式(3)中的第二项可写为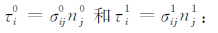
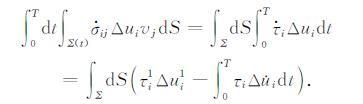
|
(4) |
假设动摩擦应力满足τi=τf为一个常数,即有
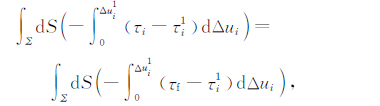
|
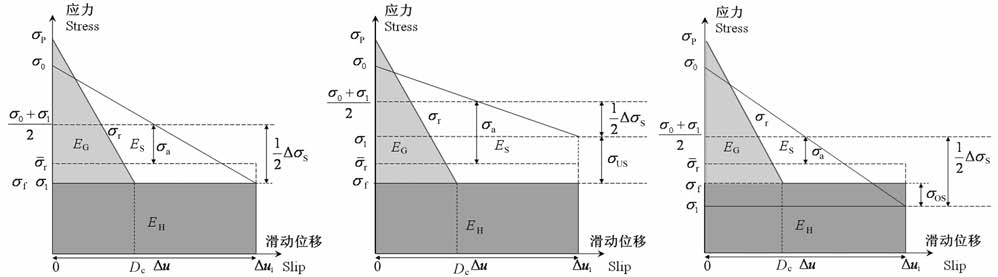
从而又回到Madariaga[1]的公式(1).而基于圆盘模型,并采用简化的滑移弱化准则,如图 2,即当Δui≤DC 时,τi=τP- (τP-τf)/DCΔui;当ΔuiDC 时,τi=τf 为一个常数.我们可以得到不依赖于模型的远场地震波辐射能的计算公式:
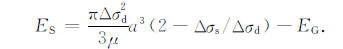
|
(5) |
如果动摩擦应力上调或者下调发生,破裂能EG =πa2(σp-σf)DC/2可由图 2的三角形面积给出,其中σP 为屈服应力,DC 为滑动弱化位移.进一步,Kanamori和Rivera[9]给出辐射效率η 可直接同破裂速度vR 相联系,有
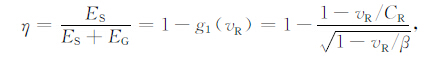
|
|
图 2 三种应力状态下的能量分配图(a)完全应力降模式;(b)应力下调模式;(c)应力上调模式.其中,σP 为屈服应力,σ0 和σ1 分别为初始应力和终止应力,σf为最终滑动摩擦应力,σr为破裂过程中滑动摩擦应力,σr为平均滑动摩擦应力,σUS 为应力下调模式下最终应力与滑动摩擦应力之差,σOS 为应力上调模式下滑动摩擦应力与最终应力之差. Fig. 2 Energy partitions based on three kinds of stress model(a) Total stress drop; (b)Undershoot; (c)Over shoot model.In which,σP is the yields tress which in dicates the streng thof fault ,σ0 andσ1 are the in it ialand final shear stress esapplied on the fault , respectively.σf andrf are the final dynamic frictional and resisting stresses, respectively.σr is the average frictional stress,σUS is the difference betweenσ1 andσf for under shoot.σOS is the difference betweenσf andσ1 for over shoot. |
其中,g1(vR)为Ⅱ型破裂模型参数.那么由M0 =7/16Δσsa3,公式(5)可写为:
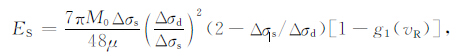
|
(6) |
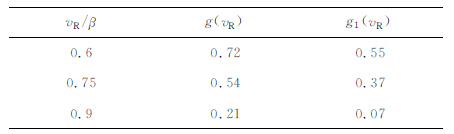
公式(6)的优越性在于,ES 的求取过程不依赖于M-模型或D-模型,它不仅是与vR/β和Δσs/Δσd 相关的连续函数,还适用于完全应力降、应力下调和应力上调的情况.而且,vR/β 与Δσs/Δσd 的取值是相互独立的.表 1给出了在vR/β 为0.6β、0.75β 和0.9β 时g(vR)与g1(vR)的取值.
|
|
表 1 在vR/β 为0.6β、0.75β 和0.9β 时g(vR)与g1(vR)的取值. Table 1 WhenvR/β is 0.6β、0.75β and 0.9β,the value ofg(vR)andg1(vR) |
当断层破裂时,近断层运动包含了造成永久形变所做的功以及伴随的高频能量辐射.那么近场能量Enf 可以表达为Enf =ES+W.对于圆盘断层而言,W=πa2ΔσsΔu/2为断层准动态的从0滑动到平均最终位移Δu的近场能量,其中:Δu=16Δσda/(7πμ)[10].由于服从滑移弱化准则,按照图 2 的能量分配关系可得Δσd =af +1/2Δσs, 因此有:

|
(7) |
因此,近场总能量应为:

|
(8) |
而远场与近场能量之比为:

|
(9) |
由此可见,远场与近场能量比值不依赖于动态应力降,也不依赖于破裂速度的大小,仅仅与远场视应力af 和静态应力降Δσs 有关.从简单滑移弱化准则得到的W结果比McGarr和Fletcher[11]的更简洁,且不依赖于破裂速度的选取.公式(9)与McGarr和Fletcher[11]由M-模型和D-模型的fM&D =af/(af+1/2Δσ)s 具有相似的形式,只是分母上略有差别.对于许多大地震能量辐射大小的统计结果表明,如果远震能量估计是准确的,Δσs/af 约为10[12].可以求得fM&D =17%,fSW =25%.而对于Δσs/af 为3[12]时,fM&D =40%,fSW =44%.由此可见,fSW 和fM&D 得到了比较相似的结果.表 2和表 3给出了当vR/β 为0.6β、0.75β 和0.9β 时,fSW 与fM 和fD 的计算结果.
|
|
表 2 M-模型与滑移弱化模型所得到的远场与近场地震波辐射能之比的关系 Table 2 2The radiated energy radio of far field and near field orM-model and slip weakening model |
|
|
表 3 D-模型与滑移弱化模型所得到的远场与近场地震波辐射能之比的关系 Table 3 The radiated energy radio off ar field and near field orD-model and slip weakening model |
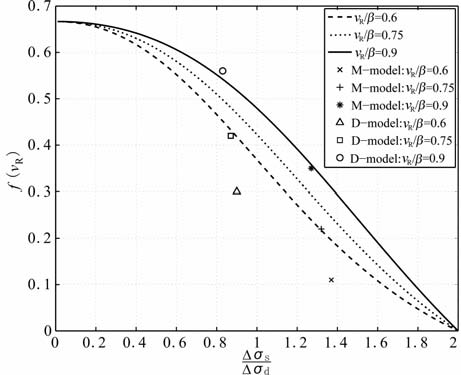
从表 2和表 3中可以看出,对于fM 和fD 模型,vR/β 的值决定了Δσs/Δσd 的值,而且在M-模型中,Δσs/Δσd 的值永远大于1,对应于动摩擦应力上调情况.而在D-模型中,Δσs/Δσd 的值永远小于1,对应于动摩擦应力下调情况.而我们所求得的远场地震波辐射能不依赖于模型的选取.为了与M-模型和D-模型作比较,我们也取vR/β = 0.6、0.75、0.9 三种情况和Δσs/Δσd 与之对应的值.从表 2 和表 3 中可以看出当Δσs/Δσd >1时,fM 取值小,fSW 也相应较小;而当Δσs/Δσd <1时,fD 取值大,fSW 也相应较大.但从总体上说,fSW 比fM 和fD 值略微偏大一些,当vR/β 接近0.9 时得到的结果几乎相等.说明目前我们的方法对于近场地震波辐射能的估计相对保守一些.
从图 3中可以看出,利用滑移弱化准则得到的是连续函数,而且Δσs/Δσd 的值不依赖于破裂速度.而M-模型和D-模型给出的数值有限,对于其他的破裂速度无法给出结果.
|
图 3 不同的破裂速度和应力降比时的远场近场辐射能之比 Fig. 3 The radiated energy radio of far field and near field for different rupture velocity ands tress drop |
在时间域上,对近场能量的估算也可用近场平均质点运动速度来表示[13]:

|
(10) |
公式(10)是对断层面积A和时间t的积分.ρ 是介质密度,β是剪切波速度,D(t)是依赖于时间的滑动位移.定义加权滑动速率或近断层质点速度${\left\langle {\dot D} \right\rangle _D}$
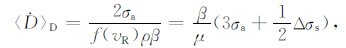
|
(11) |
公式(11)在形式上不依赖于破裂速度和动态应力降,如果远场辐射能量或视应力af 以及断层上的静态应力降Δσs 给定,那么由公式(11)可估算断层的加权滑动速率或近断层质点速度.公式(11)可用于对近断层强地面运动的速度参数给出定量化的约束.
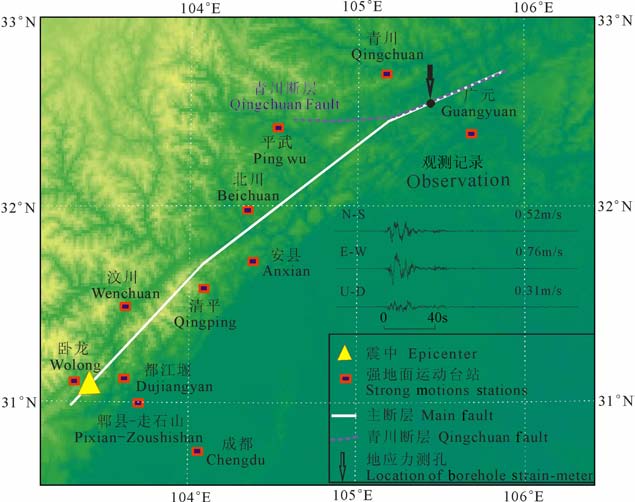
3 计算实例(1) 以汶川地震为例,通过视应力af 和静态应力降Δσs 来计算加权滑动速率.2008年5月12日四川省汶川县发生了MS8.0 地震,震源位于映秀镇(31.0°N,103.4°E).而就在汶川地震发生前一周的5月6 日,中国地震局地壳应力研究所等单位恰好在震区北端青川断裂带内部和断裂下盘的四川盆地里完成了四个测孔的水压致裂绝对应力测量,测孔深度400余米.震前,应力从四川盆地向龙门山断裂带逐渐增大,龙门山断裂带内观测点在408-418m深处附近的最大主压应力为21.8-21.9 MPa.震后,发震断裂附近的观测点390-420 m 深度段的主压应力为15.7-16.0 MPa[14],汶川地震主断层是一次以逆冲为主、兼具小量右旋走滑分量的断层.但由于断裂倾角近地表较大,约为60°-70°甚至直立,而随深度向下逐渐变缓[15],取60°倾角作为研究参数计算得到震前、震后剪应力分别为6.58 MPa和3.98 MPa, 由此得到应力降Δσs 约为2.60 MPa.根据王卫民等[16]反演得到的平均位错量2.23 m, 利用斯达尔的泊松体模型Δσs =8μD/(3πa),其中μ取3.0×1010N/m2,断层特征尺度a=22km.求得Δσs 为2.58MPa.地震矩M0 是USGS给出的7.6×1020N·m, 辐射能ES 是1.4×1016N·m, 由此求得的视应力af=0.55MPa,Δσs 取2.6MPa, 根据公式(11)可以得到 ${\left\langle {\dot D} \right\rangle _D}$ 约为30cm/s.
由于绵竹清平台站位于近断层5km 处,所以利用兰景岩等[17]给出的绵竹清平强震记录质点速度(如图 4)和王卫民等[16]反演得到的平均位错量2.23m, 可以由

|
|
图 4 汶川地震地应力测孔位置以及绵竹清平台站三分量速度记录 Fig. 4 Location of borehole strain and the velocity observation in Mianzhu Qingping in Wenchuan Earthquake |
得到汶川地震近断层的加权滑动速率或近断层质点速度,考虑到土壤层的放大效应,获得 ${\left\langle {\dot D} \right\rangle _D}$ 约为42cm/s.由于地震的高频辐射通常难以估计,所以地震波辐射能ES 的估计可能相差2-3倍[11].那么加权滑动速率 ${\left\langle {\dot D} \right\rangle _D}$ 的估计也可能相差1-2 倍.Brune[4]基于Δ$\dot{u}$=Δσdβ/μ 指出,一个应力降为3MPa的地震,得到的平均速度大约是30cm/s.那么,对于汶川地震来说,得到的加权滑动速率的结果比较符合真实情况,验证了公式(11)的有效性和实用性.
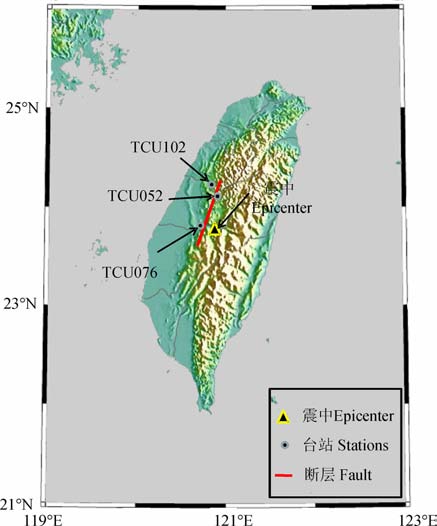
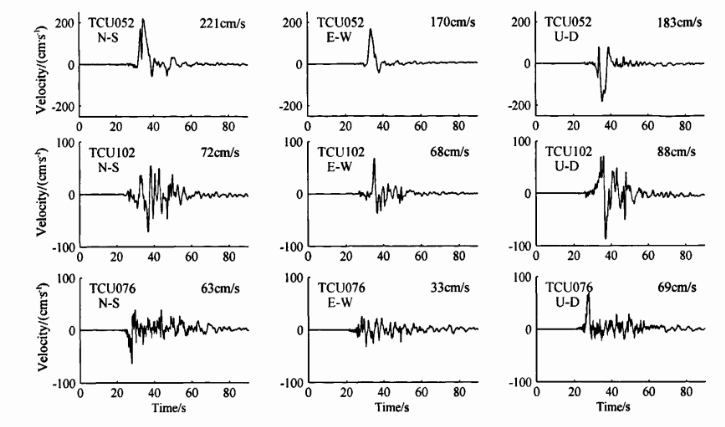
(2) 1999年9月21日在中国台湾省集集发生了MS7.6 地震.由于台网密集,我们得到了近断层台站的数据.发现得到的视应力af 和应力降Δσs 在断层北部比南部约大10 MPa[18].图 5 显示了三个近断层台站的位置,其中TCU102位于断层北部区的下盘,距离断层1.2km; TCU076 位于断层南部区下盘,距离断层3.2km; TCU052 位于断层北部区的上盘,距离断层1.8km[19].图 6显示了三分量地表质点运动速率时程曲线.通过每一个台站的三分量速率可以求得加权滑动速率,同时也可采用公式(11)对其进行估计.表 4 给出了每一个台站求得的加权滑动速率$\left\langle {\dot{D}} \right\rangle $.根据Hwang等[18]给出的远场ES/M0 的值约为5.0×105,可以得到远场视应力af=1.5 MPa.南部地区的平均滑动位移为1.5m, 而北部地区平均滑动位移为8 m[19].从表 4可以看出,利用公式(11)求得的加权滑动速率与真实地震记录得到的结果比较一致.也验证了公式(11)的有效性.
|
图 5 三个近断层台站的位置 红线代表断层,三角形代表震中位置. Fig. 5 The three near fault station The red line and triangle are the fault and the epicenter, respectively. |
|
|
表 4 集集地震三个台站近断层的加权滑动速率 Table 4 Slip-weighted average slip rate for three near fault station in Chi-Chi earthquake |
|
图 6 三分量速率曲线 Fig. 6 The three component velocity |
地震是一个复杂的动态应力变化过程.由于地下断层几何和物理结构的不确定性,使得我们对断层的形态和展布有着不同的认识.同一个地震,利用同样台站的数据,不同的学者利用不同的模型给出了不同的断层深度和倾角.这就造成对静态应力降的估计有所差别.对于同一子事件求得的静态应力降应该一样,而对于集集地震位于断层上下盘且距断层1-2km的TCU052和TCU102两个台站得到的静态应力降却相差甚远,这主要是因为没有考虑逆冲断层的几何不对称性所致.逆冲断层的上盘地表速率通常是下盘的3-4倍[20].这导致过高估计上盘的静态应力降.对于逆冲断层几何不对称对地表速率和静态应力降的影响,将在今后的研究中给予讨论.同样,由于方向性的原因,可能在某些台站得到的波形受到叠加,导致振幅增大,这样求得的动态应力降也会增大.此外,还有一些人为的不确定因素,例如不能准确地估计Brune模型中圆盘半径等,导致了不能准确求得应力降,而对于地震波辐射能的估计也存在类似的影响因素.
基于能量表象定理和滑移弱化模型,我们推导出了远场地震波辐射能的表达式.它不同于Madariaga[1]的表述,而是一个不依赖于模型选取的连续函数.之后,利用圆盘模型,我们估计了在不同的破裂速度、不同的Δσs/Δσd 时的远场与近场地震波辐射能之比.在McGarr和Fletcher[11]所讨论的三个特征点上,我们对于近场能量的估计更保守一些.最后,利用近场地震波辐射能量与加权滑移速率之间的关系,可以得到在断层面上加权滑动速率的表达式.该表达式与破裂速度和动态应力降无关.因此,通过视应力af 和静态应力降Δσs 就可获得加权滑动速率.以汶川地震和集集地震为例,求得的加权滑动速率与Brune[4]给出的结果和台站实测记录基本一致.从而,在未来的强地面运动研究中,我们对速度参数就可以给出一个合理的估计.
| [1] | Madariaga R. Dynamics of an expanding circular fault. Bull. Seisml. Soc. Am. , 1976, 66(3): 639-666. |
| [2] | Boatwright J. A spectral theory for circular seismic sources; simple estimates of source dimension, dynamic stress drop, and radiated seismic energy. Bull. Seisml. Soc. Am. , 1980, 70(1): 1-27. |
| [3] | Savage J C, Wood M D. The relation between apparent stress and stress drop. Bull. Seisml. Soc. Am. , 1971, 61(5): 1381-1338. |
| [4] | Brune J N. Tectonic stress and the spectra of seismic shear waves from earthquakes. J. Geophys. Res. , 1970, 75(26): 4997-5009. DOI:10.1029/JB075i026p04997 |
| [5] | Kanamori H. The radiated energy of the 2004 Sumatra-Andaman earthquake. In: Abercrombie R, McGarr A, Di Toro G, et al, eds. Geophysical Monograph, 170. Washington D C: American Geophysical Union, 2006. 59-68 |
| [6] | Brune J N, Thatcher W. Strength and energetics of active fault zones. International Handbook of Earthquake and Engineering Seismology, Academic Press , 2002, 81A: 569-588. |
| [7] | McGarr A, Fletcher J B. A method for mapping apparent stress and energy radiation applied to the 1994 Northridge earthquake fault zone-revisited. Geophys. Res. Lett. , 2001, 28(18): 3529-3532. DOI:10.1029/2001GL013094 |
| [8] | Rivera L, Kanamori H. Representations of the radiated energy in earthquakes. Geophys.J. Int. , 2005, 162(1): 148-155. DOI:10.1111/gji.2005.162.issue-1 |
| [9] | Kanamori H, Rivera L. Static and dynamic scaling relations for earthquakes and their implications for rupture speed and stress drop. Bull. Seisml. Soc. Am. , 2004, 94(1): 314-319. DOI:10.1785/0120030159 |
| [10] | Scholz C H. The Mechanics of Earthquakes and Faulting. Cambridge: Cambridge University Press, 1990 . |
| [11] | McGarr A, Fletcher J B. Mapping apparent stress and energy radiation over fault zones of major earthquakes. Bull. Seisml. Soc. Am. , 2002, 92(5): 1633-1646. DOI:10.1785/0120010129 |
| [12] | Abercrombie R E, Rice J R.. Can observations of earthquake scaling constrain slip weakening?. Geophys.J. Int. , 2005, 16(2): 406-424. |
| [13] | Anooshehpoor A, Brune J N. Frictional heat generation and seismic radiation in a foam rubber model of earthquakes. Pure Appl. Geophys. , 1994, 142(3-4): 735-747. DOI:10.1007/BF00876062 |
| [14] | 郭啟良, 张彦山, 王成虎等. 汶川地震构造断裂带的震前地壳深部原地应力测量. 见: 汶川8.0级地震地壳动力学研究专辑. 2009. 256-264 Guo Q L, Zhang Y S, Wang C H, et al. In-situ stress measurement in deep boreholes on the seismic faults before Wenchuan earthquake. In: Research on the Crustal Dynamics of the WenchuanMs8.0 Earthquake (in Chinese). 2009. 256-264 |
| [15] | 张永庆, 谢富仁, Gross S J. 利用2008年汶川地震序列获得的震区应力状态. 见: 汶川8.0级地震地壳动力学研究专辑, 2009. 265-276 Zhang Y Q, Xie F R, Gross S J. Background stress estimated from 2008 Wenchuan earthquake sequence. In: Research on the Crustal Dynamics of the WenchuanMs8.0 Earthquake (in Chinese). 2009. 265-276 |
| [16] | 王卫民, 赵连峰, 李娟, 等. 四川汶川8.0级地震震源过程. 地球物理学报 , 2008, 51(5): 1403–1410. Wang W M, Zhao L F, Li J, et al. Rupture process of theMs8.0 Wenchuan earthquake of Sichuan, China. Chinese J. Geophys. (in Chinese) (in Chinese) , 2008, 51(5): 1403-1410. |
| [17] | 兰景岩, 吕悦军, 彭艳菊等. 汶川8.0级强震记录的近断层效应初步分析. 见: 汶川8.0级地震地壳动力学研究专辑. 2009. 128-137 Lan J Y, Lü Y J, Peng Y J, et al. A preliminary analysis on the near-fault effect of strong-motion observations from theMs8.0 Wenchuan earthquake, China. In: Research on the Crustal Dynamics of the WenchuanMs8.0 Earthquake (in Chinese). 2009. 128-137 |
| [18] | Hwang R D, Wang J H, Huang B S, et al. Estimates of stress drop of the Chi-Chi, Taiwan, Earthquake of 20 September 1999 from near-field seismograms. Bull. Seisml. Soc. Am. , 2001, 91(5): 1158-1166. |
| [19] | Huang W G, Wang J H, Huang B S, et al. Estimates of source parameters for the 1999, Chi-Chi, Taiwan, earthquake based on Brune's source model. Bull. Seisml. Soc. Am. , 2001, 91(5): 1990-1998. |
| [20] | Oglesby D D, Archuleta R J, Nielsen S B. Earthquakes on dipping faults: The effects of broken symmetry. Science , 1998, 280(5366): 1055-1059. DOI:10.1126/science.280.5366.1055 |
 2011, Vol. 54
2011, Vol. 54