2. 哈尔滨工业大学土木工程学院, 哈尔滨 150090
2. School of Civil Engineering, Harbin Institute of Technology, Harbin 150090, China
地震断层破裂传播过程的方向性和震源辐射图效应会引起地震动及其空间分布的一些典型特征.其在单个的地震记录中可表现为时程曲线中的长周期脉冲,在整个地震动的空间分布场可表现为随方位角变化的地震动参数,比如峰值、频谱和持时等;在地震动不同分量表现为垂直断层方向的地震动峰值大于平行断层方向的地震动峰值,这就是所谓的地震动的方向性效应.从近年来所积累的观测资料中人们发现,强地面运动的幅值并不完全遵从随着震中距的增加而逐渐衰减的规律,而是在某一方向,记录波形的震相简单而幅值较高,而相反方向的记录波形却震相复杂而幅值相对较低[1,2].研究表明,当断层以接近于剪切波速的速度破裂时,在破裂的前方,地震波的能量在很短的时间内几乎同时到达某一场点,由于能量的积累效应,在速度时程的开始阶段形成一个持时相对较短、峰值较大的速度脉冲;而在背离破裂方向的场点,由于各子源破裂产生的地震波在相对较长的时间内到达,因此能量分布比较均匀,地震动的持时较长、峰值较小.这就是产生方向性效应的原因[1-7].
地震方向性效应的研究可以追溯到50多年前,Benioff[8]在1952年的加利福尼亚州科恩县MW7.5级地震的远场中长周期位移地震记录中最早发现由于破裂传播方向引起的地震动辐射随方位角变化的现象,并称这一现象为“地震多普勒效应".虽然由于断层破裂扩展的几何方位或者所谓的方向性引起的地震辐射能量随方位角的变化已被Benioff在大震的远场记录中证实,但是工程感兴趣的短周期地震动的方向性效应直到1978 年才被Bakun 等[9]证明.而后的一些研究者,如Hanksand McGuire[10],Boatw right and Boore[2],Archuleta[3]以及Abrahamson and Darragh等[11],分别从1971年San Fernando地震、1979年Coyote Lake和Imperial Valley等地震的近场强震加速度记录中发现地震动加速度也和破裂方向有关,其峰值加速度的空间分布具有明显的方向性特征,而且在地震的破裂传播方向上的工程结构的破坏也经常是最严重的[2,8,9].另外,我国的一些研究也认为尽管造成地震动方向性分布的因素很多,但震源破裂方向的影响是主要的,而且宏观烈度调查结果也表明,断层破裂方向与烈度空间分布形状的长轴,特别是内圈等震线长轴相一致,这和加速度分布相似,均受到了方向性效应的影响[12].近断层区域的地震动由于显著受到断层破裂机制、破裂传播方向以及场点位置等的影响,使得一些近断层区域的地震动与远离震源区(远场)的地震动有着显著的差别,比如近断层地震动所表现出的破裂方向性效应、上盘效应、速度大脉冲和滑冲效应等.近断层脉冲型地震动是造成近场工程结构破坏的重要因素,而地震的方向性效应是引起近断层脉冲型地震动的一个主要因素,因此研究方向性效应及其影响因素对于地震工程科学有重要的理论和实际意义.方向性效应的影响因素众多,比如震源机制、破裂速度、破裂传播方向与地震波到场点的射线方向的夹角以及断层的埋深[1]等.目前,根据已有的近断层强地震记录分析强地震动特征,再结合合理的数值方法模拟和预测某一地区可能发生的破坏性大地震所产生的强地面地震动,从而制定减灾对策是最为现实可行的防震减灾手段之一.因此,本研究基于2008 年5 月12 日发生在我国四川省境内的MS8.0级汶川地震的强地震动数据,从三个地震动基本参数分析破裂方向性对近场强震记录的影响,从而进一步揭示近场地震动方向性效应的基本特征和规律,为近场区工程结构的抗震设防提供新的依据[13].
2 强地震动数据的选取和旋转 2.1 强地震动的选取2008年5 月12 日发生在我国四川省境内的MS8.0级汶川地震造成了大量的财产损失和人员伤亡.此次地震震级大,断层的破裂时间长,破裂长度达到了300多公里,我国的强震台网在汶川地震中获得了大批的主震加速度记录[14-17],丰富了我国的近场强震数据库.本研究根据国家强震动台网中心发布的汶川地震强震数据,同时考虑到信噪比和断层距等因素,我们从中选取了198 个土层场地台站的强震记录.图 1给出了这些记录的场点位置.为了分析破裂的方向性对地震动参数的影响,根据场点与震中的相对位置以及断层的破裂传传播方向,我们将场点分为破裂前方(FD)和破裂后方(BD)两类.以震中处与断层垂直的直线为分界线,其中破裂前方的场点共105个,破裂后方的场点共93个,图1中分别用三角形和圆圈表示.
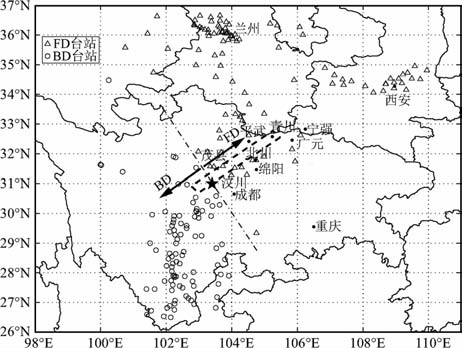
|
图 1 选取的强震台站和破裂前方、破裂后方的划分 Fig. 1 Stations used in this study and the classification of forward and back ward directions |
为了考虑破裂的方向性和破裂模式对不同水平分量的影响,同时为了给出一个可供其他地震事件参考的结果,我们将东西(EW)和南北向(NS)的记录旋转为垂直断层走向(FN)和平行断层走向(FP)的分量.图 2给出了将任意方位的一对水平正交地震动分量旋转为垂直断层和平行断层分量的方法.首先,假定β 为从NS、EW 分量旋转为FN、FP所需要的角度
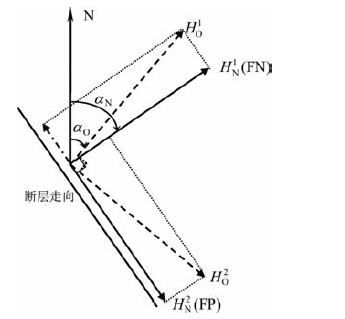
|
图 2 地震动水平分量的旋转 Fig. 2 Rotation of horizontal ground motions |

|
(1) |
那么,根据图 2可以得到旋转矩阵(R):

|
(2) |
因此,就可以得到旋转后的地震动矢量:

|
(3) |
式(3)给出了原始分量和旋转后分量之间的关系式.其中HO1 和HO2 表示原始的地震记录,αO 表示原始记录第一个分量的方位角;HN1 和HN2 表示旋转后的地震记录,αN 表示旋转后地震记录的第一个分量的方位角.
3 地震动加速度参数的方向性特征地震动的基本特征可以通过其三个要素来描述,即地震动的幅值、频谱和持时.地震动的幅值是表示地震动强弱的最重要参数之一,其中加速度峰值(PGA)在一定程度上能够表征地震本身的强度,也是最常用来描述地震动大小的参数.地震动的频谱包括反应谱和傅里叶谱等,它是频域内分析地震动特征的重要工具,反应谱描述了地震动在不同频率(周期)内对单自由度结构的最大反应,因此具有重要的工程意义.地震动的持时也是地震动本身的一个重要参数,持时包括能量持时、括号持时和工程持时等,持时对结构的破坏有重要影响:一方面持续时间的加长在结构中产生累积变形和累积破坏,另一方面也会导致某些结构因低周疲劳而丧失局部强度,另外,对于地震液化,持时有时也起着决定性作用.因此本研究分别选取地震动加速度峰值、反应谱和能量持时三个地震动的最基本的参数来研究断层破裂的方向性对地震动的影响.
3.1 峰值特征本研究从加速度峰值场的特征和峰值随距离的衰减关系两方面来分析破裂的方向性对加速度峰值的大小及其分布的影响.首先提取FN、FP 分量和竖向(UP)分量地震动加速度时程的峰值.考虑到此次地震在破裂前方的下盘地震记录较少(如图 1 所示),而绘制等值线时需要根据数据的控制点采用数值方法进行插值,如果插值时控制点较少,就可能造成等值线图形不准确.因此,为了使等值线图更加合理,本文采取了如下措施:(1)首先根据地震动台站分布图在下盘缺少控制点的区域(北纬27°-33°,东经106°-110°)适当补充控制点(如图 3a所示绿色三角);(2)然后根据这些控制点的经、纬度和和反演的有限断层的产状和几何参数,计算各个控制点到断层的断层距;(3)然后根据汶川地震198 组场点的地震动建立的衰减关系(式(4))计算各新增控制点的PGA 值,其中包括FN、FP 和UP 三个分量的值;(4)最后将由汶川地震衰减关系得到的控制点的PGA 和原来实际地震记录的198 个场点的PGA 联合,再采用克里金插值方法将所有场点PGA 进行插值,得到整个地震动峰值场的等值线图.
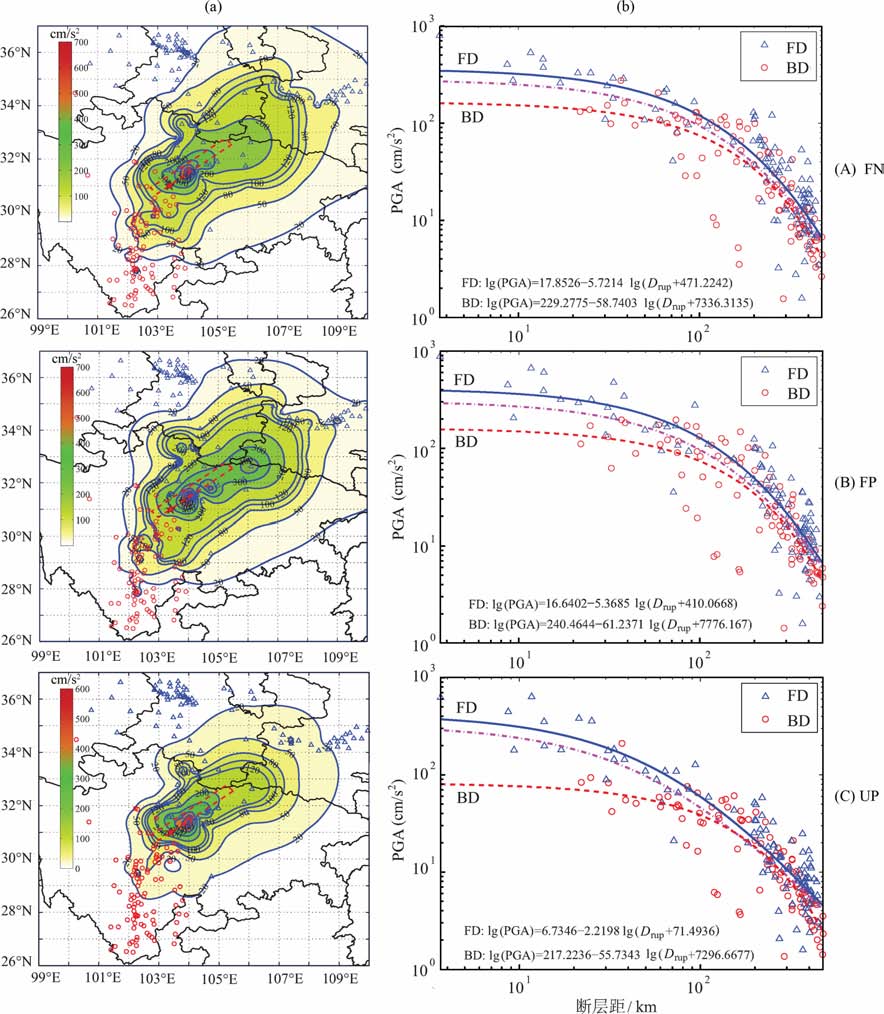
|
图 3 (a)PGA 等值线图;(b)破裂前、后方PGA 衰减关系对比.(A)FN 分量;(B)FP分量;(C)UP分量 Fig. 3 (a)PGA contour map; (b) PGA at tenuationrelations of forward and back ward direction.(A)FN component; (B)FP component and (C)UP component |
为了计算场点到断层的距离,同时为了对比地震动峰值场的分布特征与断层破裂方向的关系,本文采用了文献[18]的有限断层模型.图 3a分别给出了FN、FP和UP分量的地震动加速度峰值场等值线图.从各分量等值线图中可以看出:一方面,地震动的峰值场呈不对称的椭圆形分布,这与工程结构震害调查的烈度分布图形状一致.另一方面,地震动的峰值场表现出了明显的方向性特征.即在破裂前方(东北方向)的地震动的峰值明显大于破裂后方(西南方向)的峰值,而且破裂前方的地震动峰值衰减的较慢,破裂后方的则衰减的较快.需要注意的是,从图 3可以看出最大的峰值区域并不出现在断层破裂的末端,而是出现在了什邡和绵竹一带,这与文献[18]等反演的有限断层模型上的凹凸体出现的位置相对应,而且也与实际的震害调查(烈度)分布一致.这一点并不和方向性效应矛盾,因为对于靠近断层附近的地震动,特别是受高频分量控制的加速度峰值参数,断层面上具有较大滑动量的凹凸体对其附近的地震动起到了控制作用.
另外,为了定量分析方向性效应对峰值的影响程度,我们从破裂前方和破裂后方的地震动随距离的衰减关系的差别来证明方向性效应的影响.对于同一次地震,不考虑震级和其他参数的影响,采用如式(4)所示的峰值-距离衰减模型,其中距离项的定义采用场点到断层的最短距离Drup.
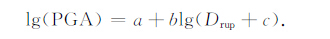
|
(4) |
分别基于破裂前方、破裂后方以及全部场点的地震动建立衰减关系,如图 3b所示.其中蓝色的实线为破裂前方场点的衰减关系曲线,红色的虚线为破裂后方场点的衰减关系曲线,粉色的点划线为所有场点的衰减关系曲线,图中FD 和BD 分别表示破裂前方和破裂后方的衰减关系曲线.对比破裂前、后方的峰值和衰减关系曲线可以看出:一方面,由破裂前方场点的峰值得到的衰减关系曲线明显高于由破裂后方的场点的峰值得到的衰减关系曲线,即相同断层距条件下,破裂前方的峰值大于破裂后方的峰值;另一方面,断层距越小,破裂前方和破裂后方的峰值的差别越大,随着断层距的增大,破裂前方和后方衰减关系的差异逐渐减小.表 1 给出了基于所有场点的峰值值回归得到的衰减模型参数.
|
|
表 1 PGA衰减关系的模型参数 Table 1 Parameters of PGA attenuation model |
地震动的反应谱是表征地震动频谱特性的一个重要参数,通过对比破裂前、后方反应谱的均值、谱比可以分析方向性效应对地震动反应谱各个自振周期段的影响.因此,我们首先计算每条地震动的5%阻尼比的绝对加速度反应谱,然后根据破裂前、后的台站分组计算各组反应谱的平均值,再根据破裂前、后方的平均反应谱计算谱比.另外,为了研究方向性效应对某一固定自振周期时反应谱谱值的影响,我们分析了同一自振周期下的反应谱谱值的等值线图.
对比图 4a给出的破裂前、后方场点的反应谱Sa及谱比图可知:在三个分量的整个自振周期段上(T=0-10s),破裂前方的反应谱平均值总是大于破裂后方的平均值.从谱比曲线可以看出,对于FN和FP分量,在周期小于2s时,破裂前方的平均反应谱是破裂后方平均反应谱的2 倍左右;当周期大于2s时,方向性效应更加明显,谱比最高可以达到4倍左右;对于UP分量,周期小于2s时破裂前、后方平均反应谱的比值在1.5-3倍之间;当周期超过2s时,破裂前、后方平均反应谱的比值可达到3 左右.因此,从平均反应谱的对比不难看出,在较大自振周期时破裂前、后方的反应谱差别更大,或者说方向性效应对长周期的结构影响会更加显著.
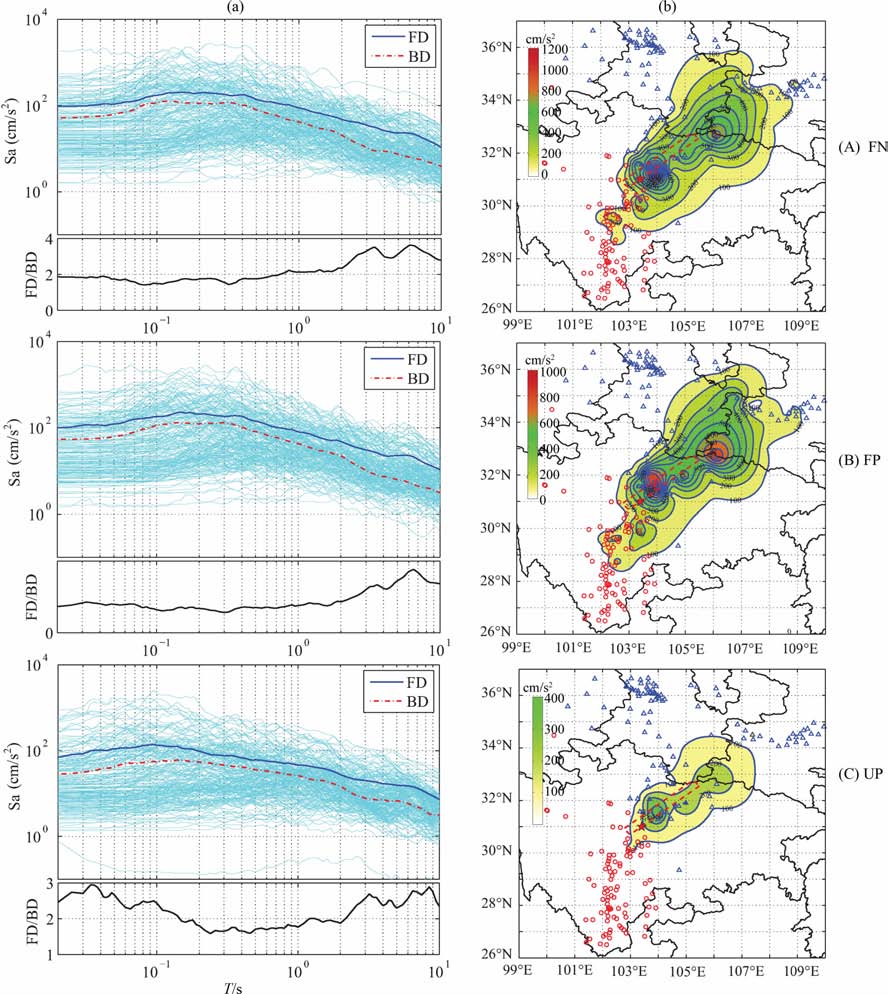
|
图 4 a)破裂前、后场点的平均加速度反应谱及谱比;(b)自振周期T=0.5s时反应谱谱值场.(A)FN 分量;(B)FP分量;(C)UP分量 Fig. 4 (a) Average response spectra of forward and backward directions ; (b) Response spectra value at natural periodT=0.5 s.(A)FN component ;(B) FP component and (C) UP component |
与绘制加速度峰值等值线图时的插值方法相同,为了使破裂前方下盘的等值线更加合理,我们在计算反应谱等值线场时在下盘缺少场点的区域适当增加了一些控制点,控制点的反应谱取值同样根据汶川地震本身建立的反应谱衰减关系得到.图 4b为自振周期T=0.5s时的反应谱谱值的等值线场,从此等值线图上可以看出方向性效应的影响,即破裂前、后方的等值线图呈不对称分布.一方面,破裂前方的反应谱值显著高于同样断层距的破裂后方的反应谱值;另一方面,从等值线图沿断层走向的衰减梯度来看,破裂前方的谱值衰减的比破裂后方的慢得多.
3.3 持时特征本研究采用Trifunac-Brady[19]定义的相对能量持时,原因在于:首先,持时是地震动的参数之一,可以与地震动的其他参数(如加速度峰值或反应谱)一并使用,因此地震动的振幅已有反映,而不必在持时中再包括它;其次,能量持时突出了大震动振幅的影响,因而采用能量持时可以比较客观地反映地震动的强震时间.地震动的相对能量是按地震动加速度的平方曲线在时间轴上的积分来计算的,比如本研究采用的90% 能量持时表示地震动的能量从达到总能量的5%到95%所需的时间.
我们从破裂前、后方的持时-距离关系模型以及持时等值线场的特征来分析方向性的影响.地震动的持时是一个受到震级、距离、场地等因素影响的参数,但是对于一次地震,在类似场地条件下,可以简单假定持时仅是距离的函数.建立如式(5)的持时-距离关系曲线模型,其中T0.9 表示90%相对能量持时,然后根据计算得到的各场点的能量持时进行回归分析,得到图 5a所示的持时-距离关系曲线.
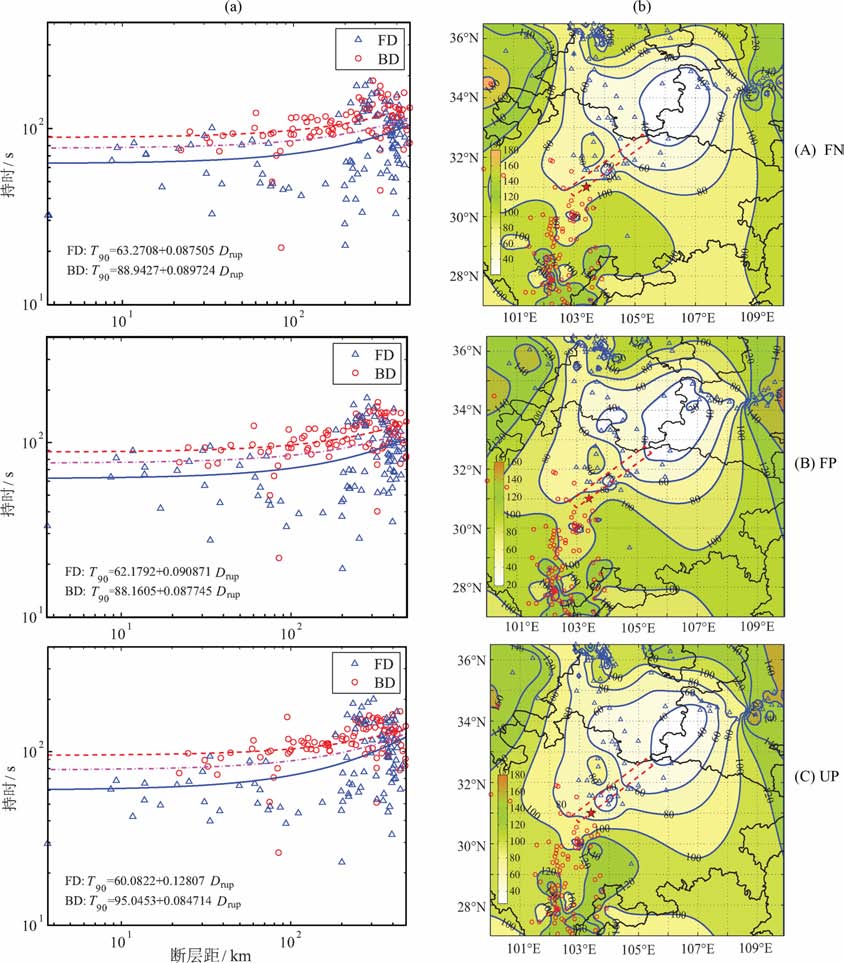
|
图 5 (a)破裂前、后方的持时的对比;(b)持时的等值线分布图.(A)FN 分量;(B)FP分量;(C)UP分量 Fig. 5 (a)Comparison of durations in forward and back ward directions; (b)Contour map of durations.(A)FN component; (B)FP component and (C)UP component |
从破裂前、后方的持时分布和持时-距离关系曲线图可发现:一方面,对于所有场点,持时随着断层距的增大有逐渐增大的趋势,这是符合理论上人们对地震动持时衰减规律的定性认识的.由于距离断层较远场点的地震动一般受到断层整个破裂过程的影响,因而地震动中包含了断层面上能量释放的各个阶段,能量分布相对比较均匀;而近断层区域的地震动在很大程度上受到了断层的局部破裂过程影响和控制,特别是当场点位于断层面上凹凸体附近时,该场点的地震动明显会受到凹凸体的控制,具有明显的强震段,因而能量分布比较集中,持时较短.另一方面,破裂前、后方的持时对比表明,破裂后方场点的持时要显著大于破裂前方的持时,这就是由于方向性效应引起的破裂前方的能量积累效应引起的,特别是当断层的破裂速度接近于传播介质的剪切波速时,断层上不同点破裂产生的地震波几乎同时到达破裂前方的场点,因而造成地震波的叠加,具有较大的峰值和较小的持时;而破裂的后方地震动的能量分布比较均匀且幅值较小,持时较长.表 2给出了基于所有场点建立的持时-距离关系模型参数.
|
|
表 2 持时模型的回归参数 Table 2 Regression parameters of duration model |
另外,为了分析方向性效应对不同方位地震动的持时的影响,我们研究了持时等值线场的分布特征.通过插值得到的地震动持时等值线场如图 5b所示.图中分别给出了各分量地震动持时的等值线图.从图中可以发现方向性效应对持时的影响非常明显,特别是在断层破裂的前方存在一个持时最小的区域,在此区域的地震动的持时仅在25s左右,其约为此次地震所有地震动持时平均值的1/3-1/4,而在破裂后方的地震动持时则相对较大.
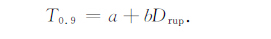
|
(5) |
汶川地震为研究近场地震动的特征提供了丰富的数据资料,基于选取的汶川地震近场强震加速度记录,按照断层的破裂朝向对地震动场点进行了分类,为了考虑方向性对不同分量的影响,我们首先根据断层的方位将水平向地震动旋转到垂直于和平行于断层走向的方向上,然后采用统计和对比的方法分析了不同破裂方向上的三分量加速度记录的峰值、反应谱和持时参数的特征.研究结果表明,汶川地震的近场强震的三个加速度基本参数具有明显的方向性特征.
(1) 对加速度峰值的分布场和峰值-距离衰减关系的分析表明:相同断层距条件下,位于破裂前方的场点的地震动的峰值明显高于破裂后方的峰值;破裂前方的地震动峰值衰减的较慢,而破裂后方的则衰减的较快.另外,从衰减曲线的对比可以看出,断层距越小,破裂前方和后方的峰值差别越大,但是随着断层距的增大,破裂前方和后方的峰值的差距逐渐减小.
(2) 对反应谱的分析表明:破裂前方的平均反应谱明显高于破裂后方的平均反应谱值,当周期小于2s时,破裂前方的平均反应谱是破裂后方平均反应谱的2 倍左右;当周期大于2s时,破裂前、后方谱比最高可以达到4倍左右.因此,方向性效应对长周期的地震动影响更加显著.从等值线图沿断层走向的衰减梯度来看,破裂前方的谱值衰减的比破裂后方的慢得多.
(3) 对地震动持时的分析表明:一方面,持时随着断层距的增大有逐渐增大的趋势;破裂后方场点的持时明显大于破裂前方,平均差别可达几倍之多,并且在破裂前方的断层末端存在一个区域,在此区域内的地震动持时在整个持时场中具有最小的值.汶川地震是一次复杂的断层破裂过程,研究表明此次地震是一次先逆冲后转为右旋走滑兼逆冲的事件[20],但是断层破裂以单侧破裂为主,破裂从震源开始后一直向东北方向破裂传播,这为产生方向性效应提供了条件,本研究的结果也证明虽然汶川地震不是一次走滑型断层地震,但是地震动的分布和衰减特征中仍表现出了显著的方向性特征.这与以往作者对类似震源机制的集集地震的研究结果有相似之处[21],集集地震发生在一个复杂的逆冲断层上,但是在断层的末端(北段)断层转变成以斜滑为主的性质.对比两次地震发现,两次地震的地震动均表现出了明显的方向性特征.但是与集集地震相比汶川地震的上盘效应则不明显,或者至少说本研究选取的土层场地台站的上下盘地震动差别不明显,究其原因,可能是由于集集地震的地震动主要是由整个断层面逆冲分量所控制[22],而汶川地震中右旋的走滑分量对地震动加速度特征起到了控制作用.
致谢感谢国家强震动台网中心提供了汶川地震的加速度记录,特别感谢评审专家提出的有益的建议和意见!
| [1] | Somerville P G, Smith N F, Graves R W, et al. Modification of empirical strong ground motion attenuation relations to include the amplitude and duration effects of rupture directivity. Seism. Res. Lett. , 1997, 68(1): 199-222. DOI:10.1785/gssrl.68.1.199 |
| [2] | Boatwright J, Boore D M. Analysis of the round accelerations radiated by the 1980 Livermore Valley earthquakes for directivity and dynamic source characteristics. Bull. Seisml. Soc. Am. , 1982, 72(6): 1843-1865. |
| [3] | Archuleta R J. A faulting model for the 1979 Imperial Valley earthquake. J. Geophy. Res. , 1984, 89(B6): 4559-4585. DOI:10.1029/JB089iB06p04559 |
| [4] | Zhang W B, Iwata T, Irikura K, et al. Dynamic rupture process of the 1999 Chi-Chi, Taiwan, earthquake. Geophys. Res. Lett. , 2004, 31: L10605. DOI:10.1029/2004GL019827 |
| [5] | Somerville P G, Irikura K, Graves R, et al. Characterizing crustal earthquake slip models for the prediction of strong ground motion. Seism. Res. Lett. , 1999, 70(1): 59-80. DOI:10.1785/gssrl.70.1.59 |
| [6] | Somerville P G. Characterizing near fault ground motion for the design and evaluation of bridges. Proceedings of the Third National Seismic Conference and Workshop on Bridges and Highways, 2002. 137-148 |
| [7] | Abrahamson N A. Effects of rupture directivity on probabilistic seismic hazard analysis. Proc. 6th Int. Conf. on Seismic Zonation, 2000. 1-10 |
| [8] | Benioff H. Mechanism and strain characteristics of the White Wolf Fault as indicated by the aftershock sequence. In: Earthquakes in Kern County, California during 1955.California Division of Mines Bulletin, 1955, 171: 199-202 |
| [9] | Bakun W H, Stewart R M, Bufe C G. Directivity in the high-frequency radiation of small earthquakes. Bull. Seisml. Soc. Am. , 1978, 68(5): 1253-1263. |
| [10] | Hanks T C, McGuire R K. The character of high-frequency strong ground motion. Bull. Seisml. Soc. Am. , 1981, 71(6): 2071-2095. |
| [11] | Abrahamson N A, Darragh R B. The Morgan Hill earthquake of April 24, 1984 -the 1.29 g acceleration at Coyote Lake dam: due to directivity, a double event, or both?. Earthquake Spectra , 1985, 1(3): 445-455. DOI:10.1193/1.1585275 |
| [12] | 刘汉兴, 汪素云, 时振梁. 考虑震源破裂方向的地震动衰减模型. 地震学报 , 1989(1): 24–37. Liu H X, Wang S Y, Shi Z L. Ground motion attenuation model considering the earthquake source rupture direction. Acta Seismologica Sinica (in Chinese) (in Chinese) , 1989(1): 24-37. |
| [13] | 胡进军. 近断层地震动方向性效应及超剪切破裂研究. 哈尔滨: 中国地震局工程力学研究所, 2009 Hu J J. Rupture directivity of near-fault ground motion and super-shear rupture (in Chinese). Harbin: China Earthquake Administration, 2009 http://www.cnki.com.cn/Article/CJFDTOTAL-GJZT201001017.htm |
| [14] | 李小军, 周正华, 于海英等. 汶川8. 0级地震强震动观测及记录初步分析. 见: 汶川地震建筑震害调查与灾后重建分析报告. 北京: 中国建筑工业出版社, 2008 Li X J, Zhou Z H, Yu H Y, et al. Strong ground motion observation and preliminary analysis of the magnitude 8.0 Wenchuan earthquake. In: Investigation and Report of Seismic Damage and Reconstruction After Wenchuan Earthquake (in Chinese). Beijing: China Architecture & Building Press, 2008 |
| [15] | Yu H Y, Wang D, Yang Y Q, et al. The preliminary analysis of strong ground motion records from the MS8.0 Wenchuan earthquake. Earthquake Engineering and Engineering Vibration (in Chinese) , 2009, 29(1): 1-13. |
| [16] | Li X J, Zhou Z H, Yu H Y, et al. Strong motion observations and recordings from the great Wenchuan Earthquake. Earthquake Engineering and Engineering Vibration , 2008, 7(3): 235-246. DOI:10.1007/s11803-008-0892-x |
| [17] | Li X J, Zhou Z H, Huang M, et al. Preliminary analysis of strong-motion recordings from the magnitude 8.0 Wenchuan, China, earthquake of 12 May 2008. Seism. Res. Lett. , 2008, 79(6): 844-854. DOI:10.1785/gssrl.79.6.844 |
| [18] | Ji C, Hayes G. Preliminary result of the may 12, 2008Mw7.9 eastern Sichuan, China Earthquake. http: //earthquake. usgs. gov/eqcenter/eqinthenews/2008/us2008ryan/ finite_fault. Php |
| [19] | Trifunac M D, Brady A G. A study on the duration of strong earthquake ground motion. Bull. Seisml. Soc. Am. , 1975, 65(3): 581-626. |
| [20] | 王卫民, 赵连锋, 李娟, 等. 四川汶川8.0级地震震源过程. 地球物理学报 , 2008, 51(5): 1403–1410. Wang W M, Zhao L F, Li J, et al. Rupture process of theMs8.0 Wenchuan Earthquake of Sichuan, China. Chinese J. Geophys. (in Chinese) (in Chinese) , 2008, 51(5): 1403-1410. |
| [21] | Hu J J, Xie L L. Directivity of near-fault ground motion generated by thrust-fault earthquake: a case study of the 1999Mw7.6 Chi-Chi earthquake. Proceedings of the 14th World Conference on Earthquake Engineering. Beijing, October 12-17, 2008, Beijing, China. Paper No. 03-02-0033 |
| [22] | Ma K F, Mori J, Lee S J, et al. Spatial and temporal distribution of slip for the 1999 Chi-Chi, Taiwan, earthquake. Bull. Seisml. Soc. Am. , 2001, 91(5): 1-19. |
 2011, Vol. 54
2011, Vol. 54


