电阻率法勘探约在19 世纪末被提出,发展到20纪初温纳和施伦贝格提出了视电阻率概念并确定了温纳四级和中间梯度装置.1989年美国一次专题会后高密度电阻率法勘探技术被提出[1~3].对于电阻率法的资料解释问题,最早可以追溯到1920年 Shchimbeger所作的研究工作.目前电阻率法资料解释的二维反演多为局部线性化的迭代反演,由 Loke编写的2D、3D 电阻率反演软件RES2DINV 和 RES3DINV取得了广泛的应用[4~12].然而电阻率二维反演是一个复杂的非线性问题,将非线性问题在初始模型附近进行线性化,必然存在反演易陷入局部极小、依赖初始模型选择等问题,因此到20世纪90年代各种非线性反演方法应运而生.非线性反演方法是通过各种途径直接求解非线性问题,实现从数据空间到模型空间的映射,基本原理就是将反演问题规划为求一个泛函极值问题的解,然后用各种优化方法解决相应的问题.非线性反演方法作为地球物理反演的一个重要分支,在地球物理反演中非线性反演方法已发挥了特有的作用,但总的来说仍处于研究阶段.非线性联合反演方法是指联合两种方法的优点,克服了它们的缺点,使反演达到最好的效果,并较好地解决了实际问题.本文就是将非线性方法蚁群算法与BP 算法联合进行高密度电法的视电阻率反演,应用于地下电法的研究.
2 电阻率二维神经网络反演 2.1 人工神经网络简介及在地球物理资料反演中的应用人工神经网络(Artificial Neural Network, ANN),是对人脑的某种模拟、抽象和简化,由三个基本要素组成:即神经元,网络结构和学习规则.具有高度的非线性映射能力、自组织和自适应能力、记忆联想能力等,能够进行复杂的逻辑操作和非线性映射.
人工神经网络在反演中的应用,大多数是基于模式识别的原理,近年来有学者从定量映射的角度将神经网络引入地球物理反演[13~15].最基本BP 网络是三层前馈网络,即输入层LA,隐含层LB 和输出层LC 之间前向连接.通常BP 网络可以有多个隐含层,可以跨层连接,可以有单元自身的反馈连接,也可以有层内单元横向连接.
和常规反演一样,基于BP 回传理论建立起来的反演方法,也要有目标函数.此时的目标函数定义为所有输入模式对的输出单元期望输出与实际输出误差的平方和:
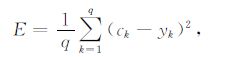
|
(1) |
其中E为均方差,是网络的能量函数,ck为第k个实际输出,yk为第k个期望输出.
和常规的反演不同,基于BP 回传理论反演过程分为学习(训练)和反演(测试)两个阶段.用于训练的输入、输出模式对(Ak,Ck),(k=1,2,…m),越多,网络用于“测试"或反演的技能越高,效果越好.可见反演所需的大部分时间耗费在学习上,只要学习好了,反演费时就少,而且精度也较高.
2.2 电阻率二维神经网络反演算例单隐含层网络训练误差收敛很慢,误差波动非常大,精度也不高,训练效果差;有两个隐含层的网络训练效果比单隐含层要好,与有三个隐含层的网络相比,比较节约时间,但计算精度略差、误差波动较大;综合考虑反演计算的精度和时间两因素,以及参考相关文献资料[17],本文确定选择有两个隐含层的四层网络进行训练.
比较附加动量法、共轭梯度法和RPROP 算法发现,在相同条件下附加动量法训练收敛非常慢,共轭梯度法训练效果较好,而RPROP 算法最好,收敛快且精度高,因此本文电阻率二维神经网络反演选择RPROP训练算法.
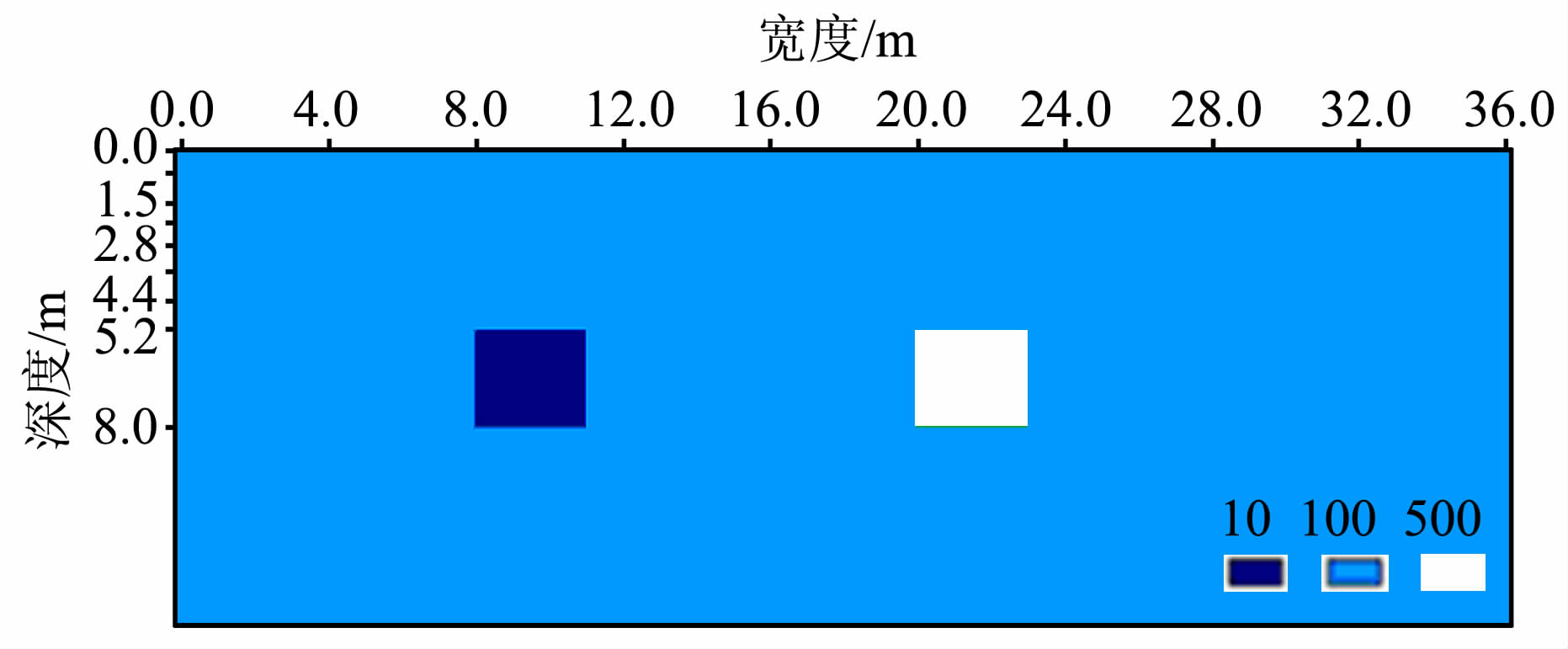
本文选择的算例模型为经典的双电阻模型1,该模型中均匀场的电阻率为100Ωm, 其中的两处异常分别为低阻10Ωm 和高阻500Ωm, 地下埋深为5m, 异常体的尺寸大小为3m×3m, 如图 1所示.模型2与模型1类似,只是将高阻异常体的电阻率定为128Ωm.
|
图 1 双阻模型1示意图 Fig. 1 Double-resistance model 1 diagram |
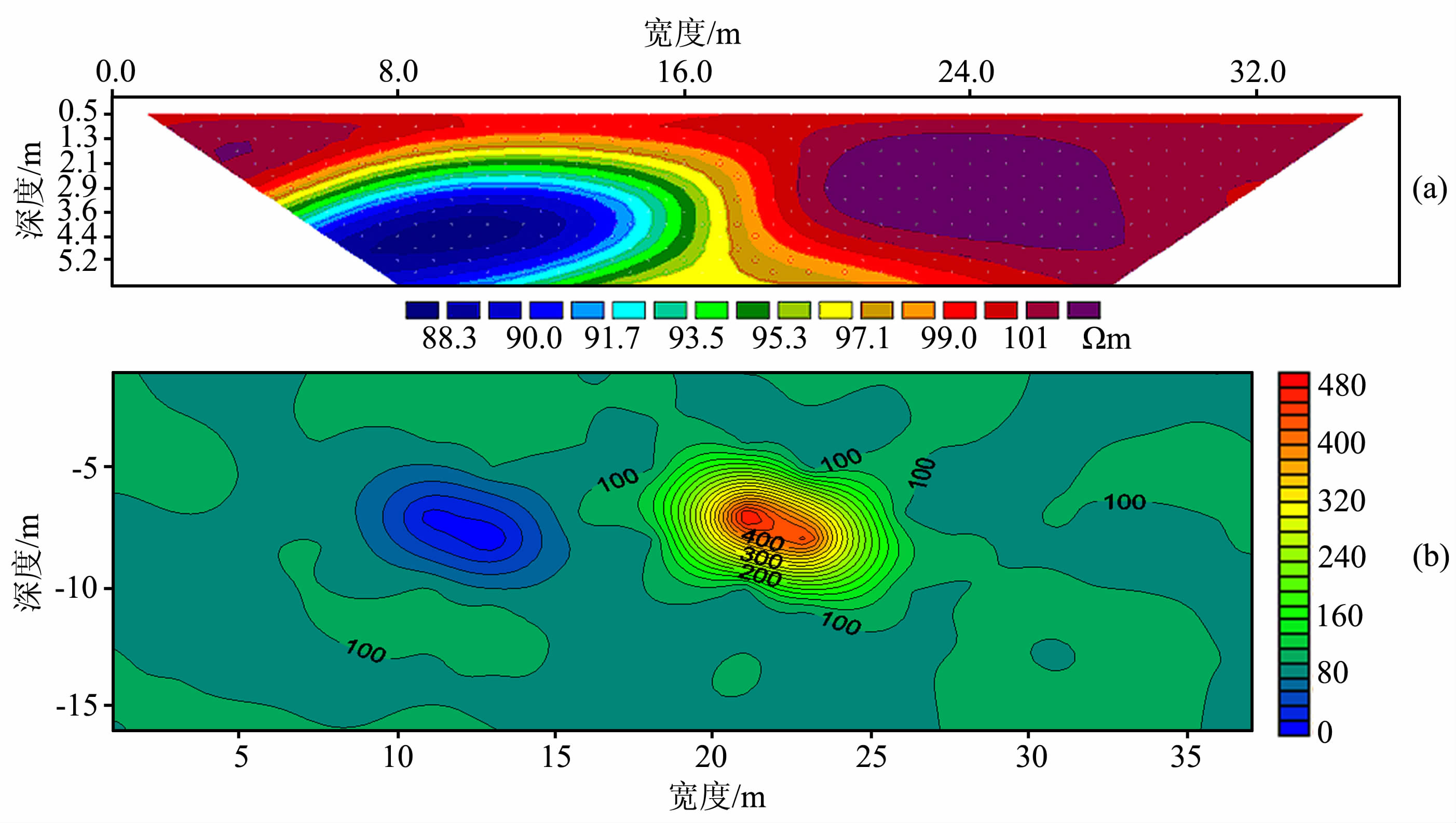
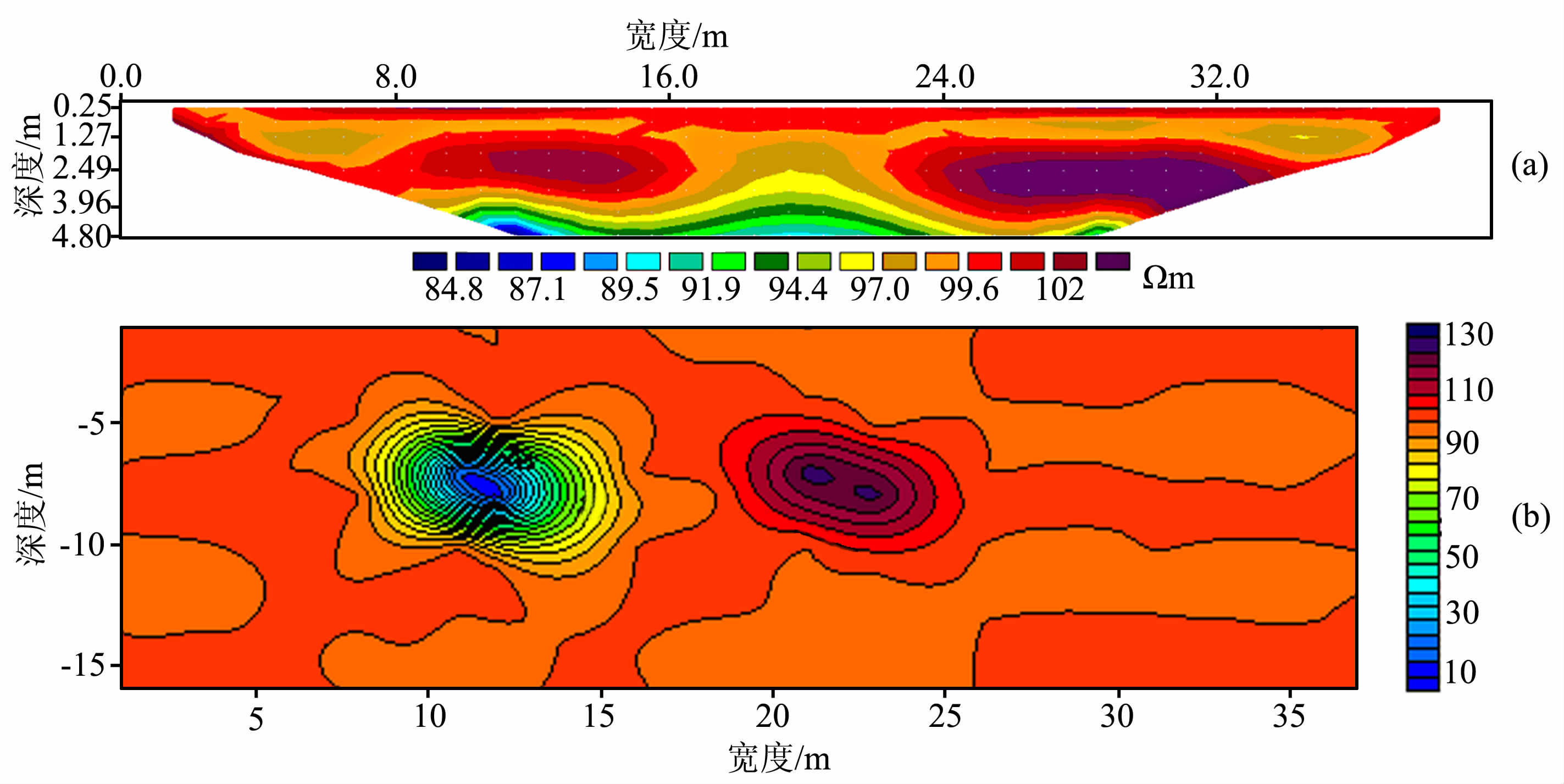
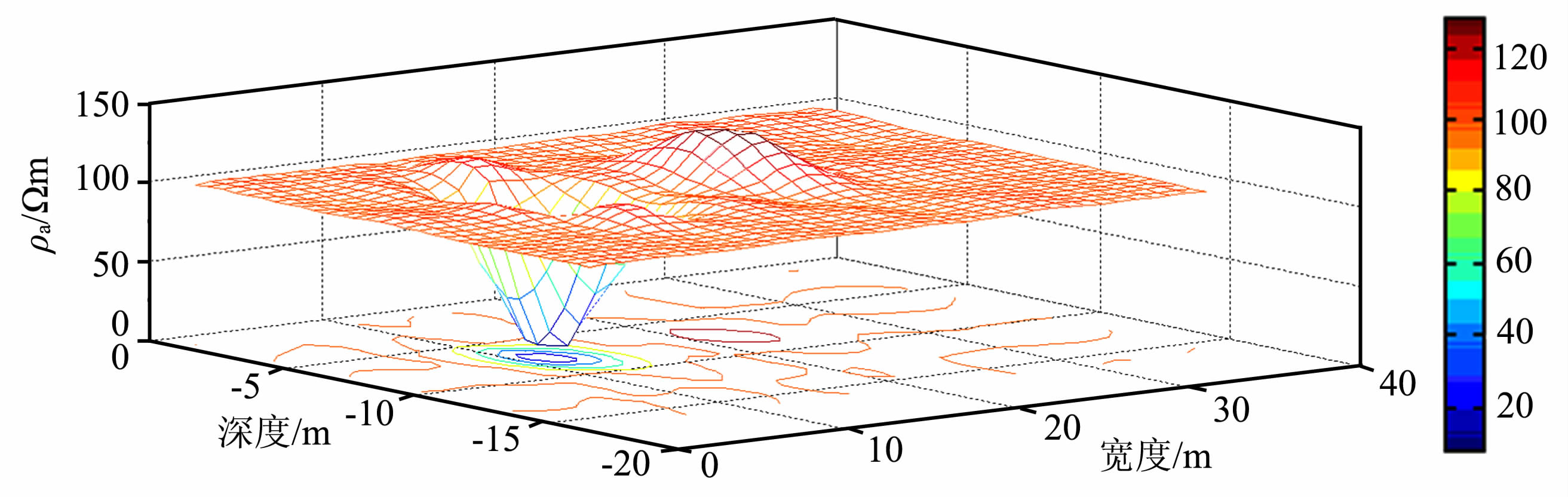
在电阻率二维BP 神经网络反演中,神经网络输入为视电阻率数据,网络输出为模型参数.因此设计网络输入层节点47个,隐含层数和各隐含层的节点数通过试错法实现最佳组合.对比了有一个隐含层的三层网络、有两个隐含层的四层网络进行训练,发现单隐含层网络训练误差收敛很慢,误差波动非常大,精度也不高,训练效果差;两个隐含层的网络训练效果比单隐含层要好,且误差波动较小,所以本文选择有两个隐含层的四层网络进行训练,两个隐层的节点数为30 和10.通过多次神经网络学习训练以及泛化能力的测试,最后得到最佳的神经预测网络,进行反演预测.在此算例中预测得到40 个点的反演预计值,然后将这些点应用到Surfer中进行成图处理,得到BP神经网络反演图 2, 图 3为模型2的反演结果.显然BP神经网络反演比RES2DINY 反演对异常体位置和电阻率值的反映更为准确;图 4为利用40个点的反演预计值在Matlab中绘制的模型1的二维反演示意图,更能清晰看到两处异常阻体的存在的空间位置.图 5 为模型2 的二维反演示意图.
|
图 2 模型1的RES2DINY 反演(a)与BP神经网络反演(b) Fig. 2 RES2DINY inversion and BP neural network inversion map of model 1 |
|
图 3 模型2的RES2DINY 反演(a)与BP神经网络反演(b) Fig. 3 RES2DINY inversion and BP neural network inversion map of model 2 |

|
图 4 模型1BP反演二维示意图 Fig. 4 Schematic diagram of model 1 two-dimensional BP inversion |
|
图 5 模型2BP反演二维示意图 Fig. 5 Schematic diagram of model 2 two-dimensional BP inversion |
蚁群算法(Antcolonyoptimization),是一种新的仿生类进化算法,由Dorigo[18, 19]等在1992 年首先提出.该算法模仿蚂蚁觅食时的行为,按照启发式思想,通过信息素(Pheromone)的诱导作用,逐步收敛到问题的全局最优解,该算法最初主要是用于求解一些NP(Non-deterministicpolynomial)问题.将ACO 与其他仿生优化方法进行融合,相互之间优势互补是蚁群算法应用的一个较活跃的应用领域.研究最早、最多的是将蚁群算法与遗传算法相结合[20, 21],Pilat等[22]采用GA 寻找最优的ACO 的参数设置,丁建立等[23]先用GA 初步寻优,取得了较好的效果;近年来将蚁群算法与人工神经网络巧妙的融合在一起是蚁群算法的又一个较活跃的研究课题,可在某种程度上避免收敛速度慢、易于陷入局部极小等问题,文献[24, 25]在这方面做了有益的探讨.
3.2 蚁群算法的原理蚁群算法的机理是:生物界中的蚂蚁在搜寻食物源时,能在其走过的路径上释放一种特有的分泌物及即信息素,使得一定范围内的其他蚂蚁能够觉察并影响其行为.蚁群算法搜索过程中,每只人工蚂蚁独立工作方式:①从起点出发;②按一定的概率转移规则确定下一个节点,修改路径轨迹强度(局部轨迹强度更新),重复这个过程直至找到目标节点;③对所有路径上的轨迹强度进行修改(全局轨迹强度更新).
4 非线性联合演算的应用 4.1 ABP神经网络训练方法针对BP算法容易陷入局部极小的不足,本文提出了ABP神经网络训练方法.ABP 方法首先利用ACO 的全局寻优能力为BP 提供σ(σ≥1)组较优的初始权值组合,以克服BP 算法容易陷入局部最优、对初值设置较敏感的缺点;再利用BP 算法梯度下降的原理进一步“细调"权值,寻找真正的全局最优点,以克服由于对定义域进行分割带来的量化误差和单一蚁群算法训练网络耗费时间过长的不足.通过与加动量项的BP 算法、演化算法以及模拟退火算法进行比较表明该方法具有更好的全局收敛性,以及对初值的不敏感性等特点[26].神经网络训练过程可看作一个最优化问题,即找到一组最优的实数权值组合,使得在此权值下输出结果与期望结果之间的误差最小,蚁群算法成为寻找这一最优权值组合的较好选择[27, 28].
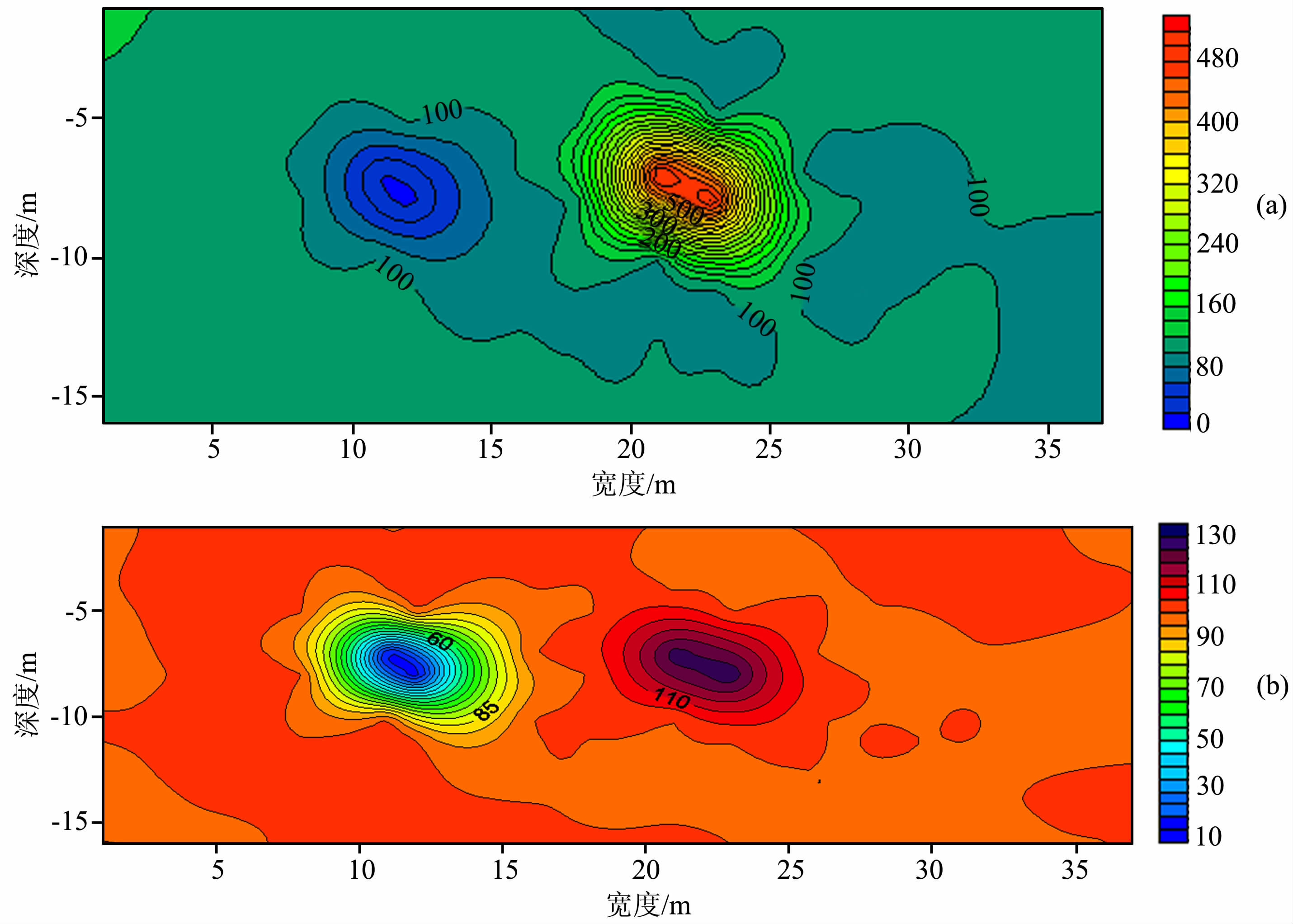
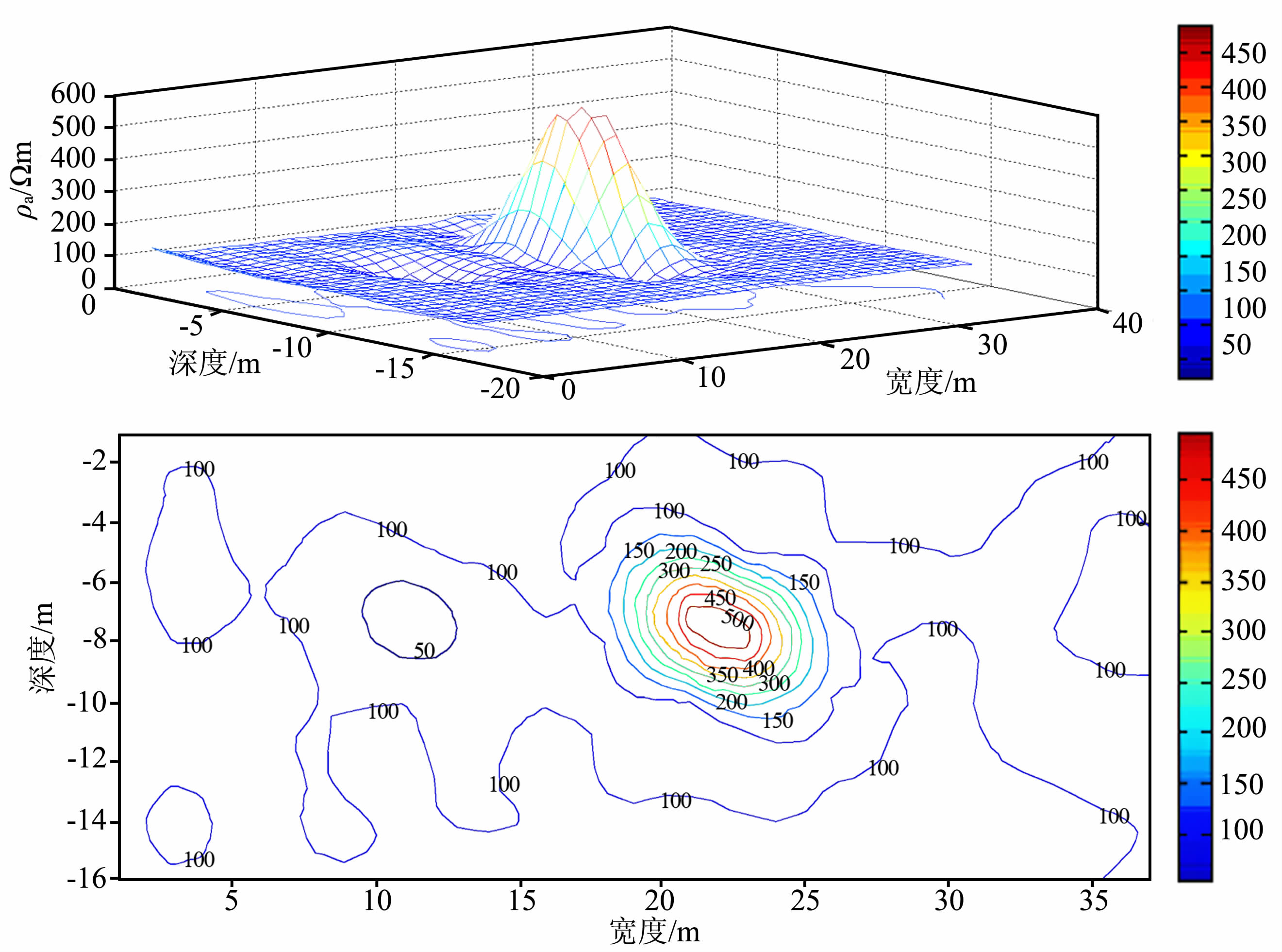
4.2 经典算例以1.2 节中的经典双电阻模型1 为例进行 ABP神经网络训练方法计算.首先利用ACO 法对要进行的47组训练数组进行初始权值、阙值的最优寻找,通过50次的迭代后,为BP 算法提供较好的训练初始值,然后再使用单隐层BP 神经网络进行训练,迭代400 次后得到最优的训练网络.40 组预测值,在Surfer中成图处理,得到ABP 神经网络反演图 6.图 7是利用ABP法得到的预测值在Matlab中绘制的模型1的二维反演示意图与二维投影图.比BP反演的精准度明显要好,反映在图上也比较规则.图 8是模型2的ABP二维反演示意图与二维投影图.
|
图 6 模型1(a)、模型2(b)的ABP方法反演图 Fig. 6 ABP inversion map of model 1(a) and model 2(b) |
|
图 7 模型1的ABP反演二维示意图和二维投影图 Fig. 7 Schematic diagram of 2-dimensional ABP inversion of model 1 |
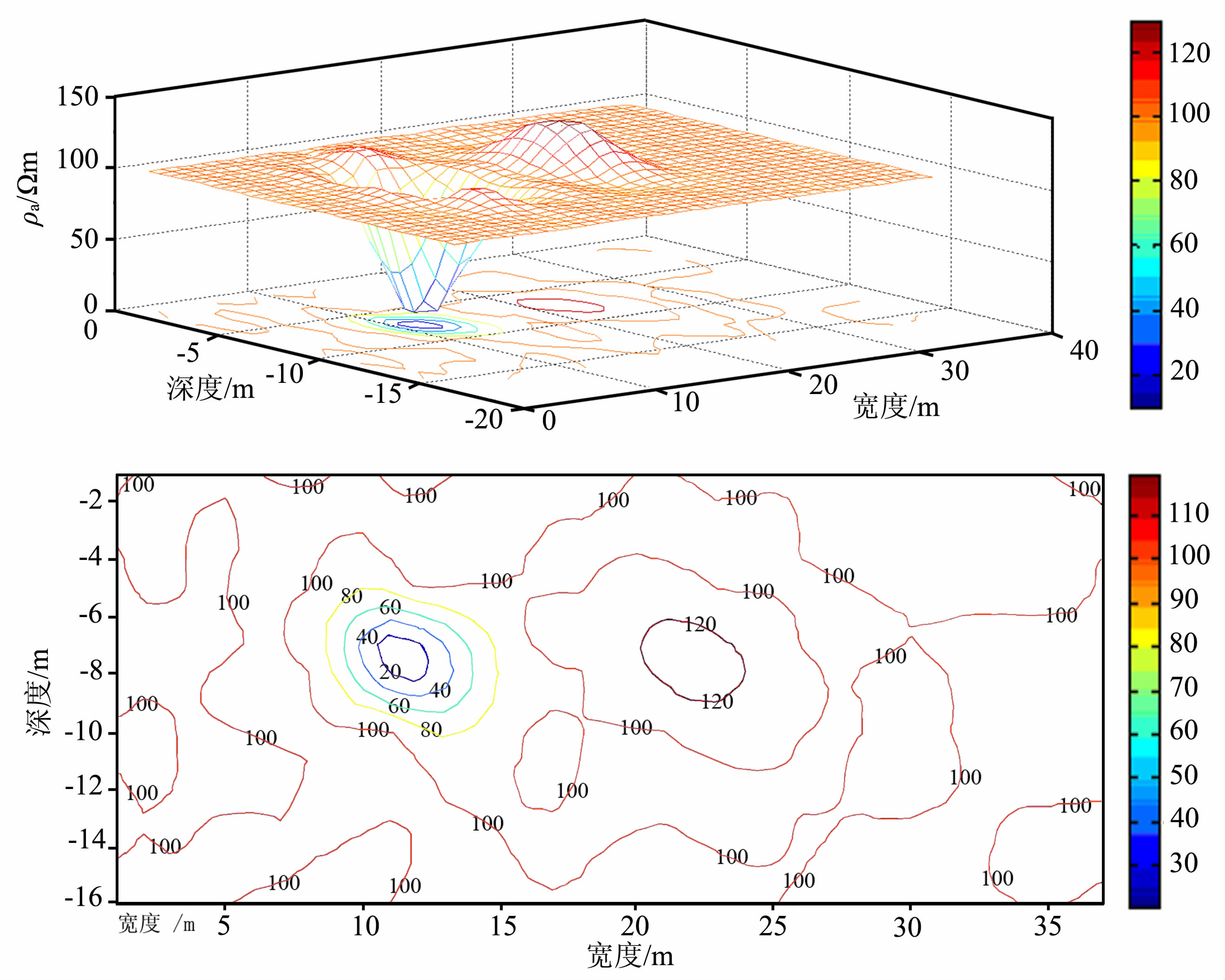
|
图 8 模型2的ABP反演二维示意图和二维投影图 Fig. 8 Schematic diagram of 2-dimensional ABP inversion of model 2 |
地球物理反演是将地球物理观测数据映射为模型参数的一种运算.这种映射既可以用模式识别的方式实现,也可以用数字的方式定量的实现.人工神经网络在反演中的应用,大多数是基于模式识别的原理,并取得了成功.从图 2的反演对比图中可以清晰地反映出非线性算法的优越性,反演计算时间短、精度高.优劣性采用判断系数R2 以及均方差E两种,评定所选取的自变量与建立的模型关系是否适合:

|
(2) |
其中,yk是期望输出平均值,ck是实际输出平均值,判定系数R2 通常用于判定自变量和因变量之间的符合度,通常介于0~1 之间,R2 越大符合性越好.E代表正确期望与网络输出值的平均差异平方,其值越小越好,因此,R2 越大、E越小则为良好的模型状态.
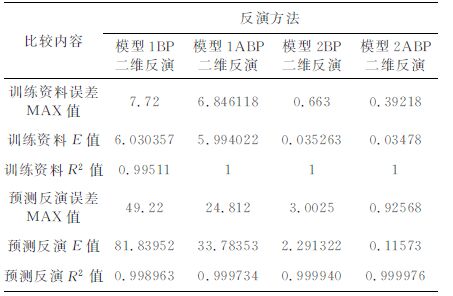
表 1为两模型分别使用BP 法和ABP 法进行反演的结果对比表,由此得到以下结论:
|
|
表 1 两种反演算法结果对比 Table 1 Contrast of two inversion algorithm s results |
(1) 从两种网络的误差最大值MAX 项来看,ABP神经网络明显好于BP 神经网络,预测中前者 MAX 值均低于后者,说明后者在训练中误差较大或者训练失败比例较高.
(2) 误差均值稳定性的对比.ABP 神经网络的检验误差基本与误差均值相差不大,稳定性好,波动较小;而BP神经网络的检验误差波动性就较前者大,表明神经泛化能力不及前者.
(3) 均方差是表明数据稳定性的参数.从两种神经网络方法的E值来看,ABP 要优于BP 算法,在模型1中预测时前者为33.78,后者高达81.84.
(4) BP神经网络法进行反演时需要用双隐层才可以获得较好的网络进行预测,需要多次调整隐层节点数,因此迭代次数较多、费时较长;而ABP法反演时,由于ACO 先优化了BP 神经网络初始权值、阙值,所以在训练时仅单隐层网络就可得到更优的结果,时间也相对快些.
因此,通过上述四点的对比,可见ABP 神经网络算法无论是训练成功率还是数据稳定性都要明显好于BP算法.
5 结语电阻率二维反演是一个复杂的问题,将非线性方法应用于它的反演得到了认可,BP算法就是其中一种较好的方法.随着非线性联合方法的深入研究,为避免单独使用BP 神经网络易陷入局部极小、依赖初始权值选择、反演时间长的缺点,文中提出将 ACO 与BP方法联合的ABP 非线性反演法,通过经典模型---地下双阻异常体的对比反演计算,清楚地反映出了ABP算法的优越性及可用性.
| [1] | 祁民, 张宝林, 梁光河, 等. 高分辨率预测地下复杂采空区的空间分布特征-高密度电法在山西阳泉某复杂采空区中的初步应用研究. 地球物理学进展 , 2006, 21(1): 256–262. Qi M, Zhang B L, Liang G H. High-resolution predict the ground to gather the area of space complex distribution- High density electricity in shanxi yangquan a complex pick up in the initial application. Progress in Geophysics (in Chinese) , 2006, 21(1): 256-262. |
| [2] | 祁民, 张宝林, 梁光河. 高密度电法的三维数据场可视化. 地球物理学进展 , 2006, 21(3): 981–986. Qi M, Zhang B L, Liang G H. The visualization of three dimension data fields of high density electrical technique. Progress in Geophysics (in Chinese) , 2006, 21(3): 981-986. |
| [3] | Sehlmubeger C. Etude surla prospection electique du sous-sol. 1920 . |
| [4] | 杨文采. 地球物理反演的理论与方法. 北京: 地质出版社, 1996 . Yang W C. The Theory and Method of Geophysics (in Chinese). Beijing: Geological Publishing House, 1996 . |
| [5] | Backus G E, Gilbert J F. Numeficfl application of a formulism for geophysical problem. Geophys. J. R. astr.Soc. , 1967, 13: 247-276. DOI:10.1111/gji.1967.13.issue-1-3 |
| [6] | Backus G E, Gilbert J F. The resolving power of gross earth data. Geophys. J.R.astr. Soc. , 1968, 16: 169-205. DOI:10.1111/gji.1968.16.issue-2 |
| [7] | Wiggins R A. The generalized linear inverse problem:Implication of surface waves and free oscillations for earth structure. Rev.Geophys. Space Phys. , 1972, 10: 251-285. DOI:10.1029/RG010i001p00251 |
| [8] | Jackson D D. Interpretation of inaccurate, insufficient and inconsistent data. Oeophys. J. R. astr. Soc. , 1972, 28: 97-109. DOI:10.1111/j.1365-246X.1972.tb06115.x |
| [9] | Parker R L. Understanding inverse theory. Rev Earth Planet Sci , 1976, 5: 35-64. |
| [10] | 艾伯特•塔兰托拉. 反演理论一数据拟合和模型参数估计. 北京: 学术出版社, 1989 . Albert•Talantula. The Theory of Inversion-Data and Estimates Proposed Model Parameters (in Chinese). Beijing: Academic Press, 1989 . |
| [11] | 王家映. 地球物理反演理论. 武汉: 中国地质大学出版社, 1998 . Wang J Y. Geophysical Theory of Inversion (in Chinese). Wuhan: China University of Geosciences Press, 1998 . |
| [12] | 何继善. 电法勘探的发展与展望. 地球物理学报 , 1997, 40(Suppl): 308–316. He J S. The prospecting only development and prospect. Chinese J.Geophys. (in Chinese) , 1997, 40(Suppl): 308-316. |
| [13] | 李创社, 张彦鹏, 李实, 等. 瞬变电磁勘探中的人工神经网络反演法. 西安交通大学学报 , 2001, 35(6): 604–615. Li C S, Zhang Y P, Li S, et al. New inversion method of artificial neural network in transient electromagnetic inversion. Journal of Xi'an Traffic University (in Chinese) , 2001, 35(6): 604-615. |
| [14] | 黄科, 肖慈殉, 张哨楠, 等. 基于神经网络的储层识别处理技术及在塔河油田的应用. 物探化探计算技术 , 2006, 28(1): 18–21. Huang K, Xiao C X, Zhang S N, et al. Based on the nerve network layer of recognition processing technology and applications in the field of Tahe. Computing Technology for Geophysical and Geochemical Exploration (in Chinese) , 2006, 28(1): 18-21. |
| [15] | 丁柱, 杨长春, 陶宏根, 等. 神经网络反演双侧向电阻率测井曲线的物理约束. 地球物理学进展 , 2002, 17(2): 331–336. Ding Z, Yang C C, Tao H G, et al. The nerve network the performance of the logs to the resistivity of the physical constraints. Progress in Geophysics (in Chinese) , 2002, 17(2): 331-336. |
| [16] | 徐海浪, 吴小平. 电阻率二维神经网络反演. 地球物理学报 , 2006, 49(2): 584–589. Xu H L, Wu X P. 2-D resistivity inversion using the neural network method. Chinese J. Geophys (in Chinese) , 2006, 49(2): 584-589. |
| [17] | 王家映. 人工神经网络反演法. 工程地球物理学报 , 2008, 5(3): 255–265. Wang J Y. The artificial neural network method. Chinese Journal of Engineering Geophysics (in Chinese) , 2008, 5(3): 255-265. |
| [18] | Colorni A, Dorigo M, Maniezzo V. Maniezzo V.Dist ributed optimization by ant colonies. Proc of the First European Conference on artificial Life.Paris. France: Elsevier Publishing, 1991 : 134 -142. |
| [19] | Colorni A, Dorigo M, Maniezzo V. An investigation of some properties of an ant aigorithm . Proc of the Parallel Problem Solving from Nature Conference(PPSN'92). Brussels, Blegium: Elsevier Publishing, 1992 : 509 -520. |
| [20] | Gong D X, Ruan X G. A hybrid approach of GA and ACO for TSP. Proceedings of the 5th World Congress on Intelligent Control and Automation, Hangzhou, China , 2004, 3: 2068-2072. DOI:10.1109/WCICA.2004.1341948 |
| [21] | Kumar G M, Haq A N. Hybrid genetic-ant colony algorithms for solving aggregate production plan. Journal of Advanced Manufacturing Systems , 2005, 4(1): 103-111. DOI:10.1142/S021968670500059X |
| [22] | Pilat M L, White T.Using genetic algorithms to optimize ACS-TSP.Proceedings of Ant Algorithms:Third International Workshop, ANTS 2002, Brussels, Belgium, 2002. 282~287 |
| [23] | 丁建立, 陈增强. 遗传算法与蚁群算法的融合闭. 计算机研究与发展 , 2003, 40(9): 1351–1356. Ding J L, Chen Z Q. The method combinating genetic algorithm with the group of algorithms. Journal of Computer Research and Development (in Chinese) , 2003, 40(9): 1351-1356. |
| [24] | Hong B R, Jin F H, Guo Q. Hopfield neural network based on ant system. Journal of Haerbin Institue of Technology , 2004, 11(3): 267-269. |
| [25] | 邹政达, 孙雅明, 张智晟. 基于蚁群优化算法递归神经网络的短期负荷预测. 电网技术 , 2005, 29(3): 59–63. Zou Z D, Sun Y M, Zhang Z S. The short-term forecast of the algorithm based on the number of recursive neural network. Power System Technology (in Chinese) , 2005, 29(3): 59-63. |
| [26] | 张国立, 王晶, 谢宏, 等. 利用蚁群算法优化前向神经网络. 电子商务 , 2005, 18: 65–67. Zhang G L, Wang J, Xie H, et al. Using of the ant colony algorithm to optimize neural network. E-business (in Chinese) , 2005, 18: 65-67. |
| [27] | 刘彦鹏. 蚁群优化算法的理论研究及其应用. 杭州: 浙江大学出版社, 2007 . Liu Y P. The ACO theory researching and application (in Chinese). Hangzhou: Zhejiang University Press, 2007 . |
| [28] | 王书明, 刘玉兰, 王家映. 地球物理资料非线性反演方法讲座-蚁群算法. 工程地球物理学报 , 2009, 6(2): 131–135. Wang S M, Liu Y L, Wang J Y. ant colony optimization. Chinese Journal of Engineering Geophysics (in Chinese) , 2009, 6(2): 131-135. DOI:10.1088/1742-2132/6/2/004 |
 2011, Vol. 54
2011, Vol. 54