随着社会工业对油气资源的需求不断增长,地震勘探技术也在不断发展,面临着越来越复杂的地质勘探任务.在碎屑岩地震勘探中,油气藏的寻找由简单构造、大型构造和浅中层构造向小型、复杂构造和深层构造发展.面向的地质目标也日益复杂,如陡倾角、多断裂、横向非均匀性较大的构造等.另外,中国的海相碳酸盐岩油气勘探也进入发展的高峰期.碳酸盐岩储层类型复杂多样,孔、缝、洞型储层在碳酸盐岩油气储层中占据了重要位置,勘探开发面临储层非均质性强、绕射和散射地震波场发育、地震波场十分复杂等诸多难题.
随着地震勘探面临的勘探任务越来越复杂,地震勘探成效在很大程度上,取决于对基于符合实际介质模型的方法理论研究[1].从地震波传播的角度,我们知道,早期的地震波传播规律研究都是基于均匀各向同性、完全弹性介质中的传播理论.但是面对目前复杂的地震勘探,这种理想的假设已经不能满足勘探的需要,我们必须考虑更为复杂的介质特性,如介质的非均质性和各向异性.
一般的有限差分地震模拟方法是规则的交错网格,是处理非均匀介质,特别是连续非均匀介质波动问题的有效方法.当模拟强纵横向变速介质时网格间距必须取得很小,以保证计算精度和稳定性,而这样做明显地降低了计算效率.为此,人们发展了基于可变网格和不规则网格的地震波数值模拟方法.
基于可变网格和不规则网格的地震波数值模拟方法对地质模型的离散化更为合理.在纵横向速度梯度变化较大的区域、低速带和复杂构造区域,局部网格可以划分的相对精细一些,这就避免了对整个模型以精细网格模拟而导致的采样过密,避免了计算耗时长、占用内存多等问题.同时,对于保持模型计算的灵活性也非常重要.从空间采样的角度考虑,最有效的提高模拟精度同时又降低计算机内存需求的方法,就是在模型的不同区域采用不同的网格步长,即变网格(也称为不规则网格).
但是在数值模拟中,由于稳定性条件的限制,当空间网格变化时,时间稳定性仍然必须满足最短波长的原则,即时间采样需要满足精细网格采样对应的稳定性条件.例如,当模拟碳酸盐岩中的裂缝储层时,我们需要选择用毫米级或厘米级的网格来表征裂缝区域,这时时间采样间隔往往要取到微秒级.可见仅仅从空间网格变化的角度来考虑计算效率的提高是不够的,因此在变网格的基础上,本文又发展了局部变时间来配合变网格技术.在全局时间层内,对需要精细划分的空间区域进行局部时间层精细采样.时间采样变得宽松,才使得计算效率提高从根本上得到解决.
简单的不规则网格可以通过沿x轴和z轴取不同的网格间距来实现.对于弹性波的情况,Jastram和Behle(1992)[2]、Tessmer(1994)[3]、Oprsal 和 Zahradnik(1999)[4]以及Pitarka(1999)[5]分别提出了构建不规则网格的方法.早期的变网格算法是在规则的矩形网格基础上实现的,在精细网格和粗糙网格的过渡区域往往要使用插值算法来得到每一时刻的波场值.Wang 等(2001)[6]利用不规则网格实现了对黏弹性介质的模拟,在他们的算法中需要在波数域对过渡区域进行插值计算,并且只能适应2倍和3倍的空间网格变化.在正演模拟中时间算子作为一个全局变量,局部变化非常困难.Falk 等(1998)[7]、Tessmer (2000)[8]发展了二阶运动方程的变时间算法,但是对一阶速度-应力方程中时间采样是在半程上交错计算的情况并不适用.Hayashi等(2001)[9]用3倍的精细网格对近地表的低速区域实现了不规则网格正演模拟.
本文提出的双变网格有限差分算法,无须遵从稳定性条件对满足最短波长的原则的要求,可以在粗糙网格的稳定性要求下对局部进行时间和空间采样的加密,并且在每一全局时刻的空间波场值不需要插值计算,使插值计算集中在时间过渡区域,既提高了计算精度也解决了相对的计算效率问题.本文利用提出的双变有限差分算子实现了时间步长的局部变化,并且在误差控制范围内能够将局部时间步长迭代上千次.
2 交错网格变步长思想各向同性非均匀介质的弹性波一阶速度-应力方程为[10, 11]
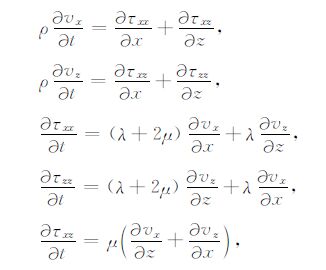
|
(1) |
其中,vx,vz表示速度,τxx,τzz,τxz表示应力向量.ρ为密度,λ,μ 为拉梅常数.求解运动方程(1)一般采用交错网格有限差分法,时间二阶精度的差分格式.在交错网格计算中,速度分量和应力分量定义在网格的半程点上,同样时间采样也是在半程上交错计算.运动方程的离散形式为
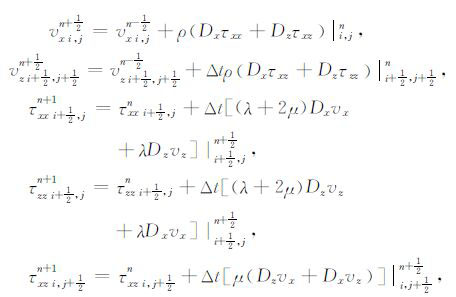
|
(2) |
式中,Dx,Dz分别表示对x,z的一阶微分算子.Δt表示时间步长.用变量g来表示速度vx、vz或应力张量τxx、τzz、τxz.交错网格常步长的任意偶数阶精度空间差分为[12, 13]
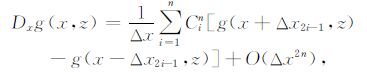
|
(3) |
式中,差分系数Cin由在x处将g(x+Δx2i-1,z)和g(x-Δx2i-1,z)作Taylor展开而得到.求解差分系数的矩阵如下:
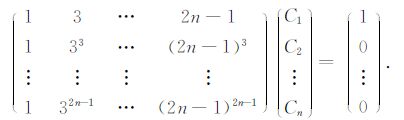
|
(4) |
从对矩阵求解可以看出,常网格算子的差分系数同网格步长无关,同算子的对称点也无关.
交错网格变步长的任意偶数阶精度空间差分为[14]
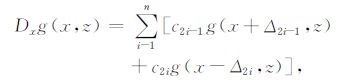
|
(5) |
式中,ci为差分系数,Δi是空间差分算子,它是网格步长dx的函数.求解差分系数的矩阵为
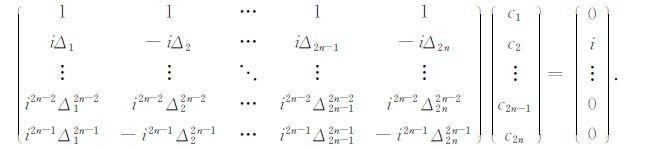
|
(6) |
这种处理网格变化的方法非常简便,在粗细网格过渡区域不需要重复设置计算区域,空间的差分精度也不需要有任何改变.它完全继承了交错网格常步长的计算简单的优点,只需要前期求解出差分系数,便可以在每一计算时刻引用.
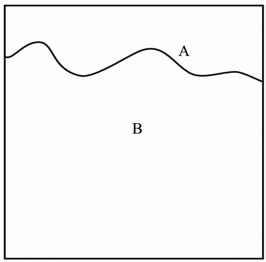
3 LVTS(局部时间步长变化)的基本思想以表层低降速带模型为例(图 1),速度模型含有几十米的低速带,若是对整个速度模型进行精细划分,那么下伏的高速区域就会过采样,整个模型的计算量是巨大的.若是对速度模型使用宽网格进行模拟,近表的低降速带会产生频散,还有可能使计算出现不稳定问题.针对这个问题,本文把整个速度场模型划分为三大部分(图 2),低降速带区域A 以精细网格表示,中深层高速区域B 用粗糙网格表示,过渡区域是一定数量的精细网格和粗糙网格相互重叠的区域.
|
图 1 低降速带模型 Fig. 1 Low velocity model |

|
图 2 表层低降速带模型网格剖分 Fig. 2 Grid generation of surface low-velocity model |
为了实现局部时间步长的变化,在粗细网格之间需要设置重叠计算区域(过渡区域).因为采用的是交错网格离散方式,因此空间步长和时间步长变化的倍数都必须为奇数倍,即1,3,5,7,9,…,2n+1.假设粗糙网格步长为精细网格步长的5 倍,如图 5所示,在一个常规时间步长内,局部区域的时间迭代需要经过5次计算.
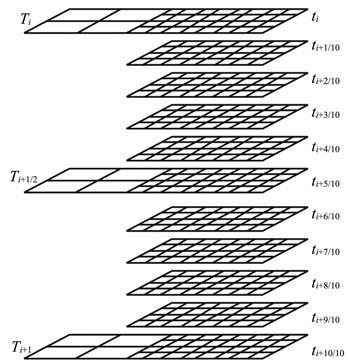
考虑速度场为二维的情况,区域B 的空间网格步长ΔH为区域A 的空间网格步长Δh的5倍,对应的区域B 的时间采样步长ΔT为区域A 的时间采样步长Δt的5倍.假设下标k代表时间采样间隔为5Δt,区域B 的速度分量初始时刻为tk-1/2,应力分量初始时刻为tk.区域A 的速度分量初始时刻为tk+3/10,应力分量初始时刻为tk+4/10.图 3和图 4分别为不同网格步长和不同时间步长的表征方式.

|
图 3 空间网格变化 Fig. 3 Locally variable space grids |
|
图 4 局部时间变化 Fig. 4 Locally variable time steps |
求解微分方程需要初始值和边值条件.时间层计算中,精细空间时间平面边界处理论上是不应该存在边值问题的.即地震波在整个时间平面上不应该产生因采样变化而导致的人工反射,而是视为一个无障碍传播的情况.因此在每个精细时间层的边界部分都需要获得一个初始值.本文采取变网格差分和插值相结合的方法来计算过渡区域的边界部分(即精细时间采样平面的边界部分).
假设空间差分为四阶精度,且已知ti-1/2 时刻Vx,Vz和ti时刻τxx,τzz,τxz的波场值,已知ti+3/10 时刻vx,vz和ti+4/10 时刻txx,tzz,txz的波场值.首先计算ti+1/2 时刻区域Bz≥zj+2 的Vx,Vz值;计算t=tk+5/10 时刻区域Az≤zj-2/5 时vx,vz波场值;然后利用交错网格变步长的空间差分公式(5)计算t=tk+5/10 时刻过渡区域zj-1 ≤z≤zj+1 内的vx,vz.并将过渡区域zj-1 ≤z≤zj+1 的vx,vz赋值给区域B对应点的Vx,Vz.例如:
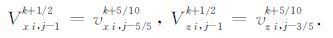
|
用和第一步相同的方法求解ti+1 时刻z≥zj的τxx,τzz,τxz值和ti+3/2 时刻z≥zj+2 时Vx,Vz值.然后根据已知的Vx,Vz值求解vx,vz值.利用双线性插值公式(7)求解精细时间采样平面(t=tk+6/10,tk+7/10,tk+8/10,tk+9/10)的边界值:
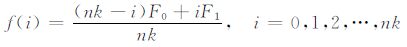
|
(7) |
其中F0,F1 表示待求点f(i)的前一全局时刻和下一全局时刻的波场值.相同边界处的应力值txx,tzz,txz也是用同样的方法利用相邻两个全局时刻的τxx,τzz,τxz值计算得到.
然后利用计算精细采样平面内部z≤zj-2/5 的vx,vz值和txx,tzz,txz值,对z=zj-1/5 处,用二阶空间采样精度计算横向上每一点的速度值.这里需要注意一个问题,当使用高阶差分算子时,边界邻近点无法用高阶差分算子计算,需要降阶处理.假设使用八阶差分算子计算网格点时,边界邻近点则需要依次用二阶、四阶、六阶差分算子来近似.但是这种降阶处理不会降低模型整体的计算精度,因为这部分网格点的时间计算次数是外部粗糙网格时间计算次数的(2k+1)倍.(k=1,2,3,…).最后用交错网格变步长的空间差分公式(5)计算t=tk+10/10 时刻z≤zj-1的txx,tzz,txz值.并将过渡区域zj-1 ≤z≤zj+1 的txx,tzz,txz值赋予区域B对应点的τxx,τzz,τxz.例如:
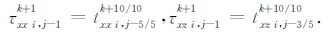
|
从算法实现过程也可以看出,当粗糙网格步长为精细网格步长的3 倍时,相应的全局时间采样也为局部时间采样的3倍,此时算法误差是最小的.因为在这个倍数的计算过程中,过渡区域的时间层边界不需要插值计算.
文中插值计算只用于精细网格区域的边界部分(即过渡区域),因此过渡区域的宽度设置非常重要,它直接决定了计算稳定性和插值计算量.一般情况下,根据变步长的任意偶数阶精度空间差分公式(5),可以看出过渡区域与网格变化范围无关,只受差分计算精度控制.当空间差分精度为m时,过渡区域的宽度应设为m/2+1.另外由于插值计算区域比较窄且集中,因此从整体上来说本文的算法仍然属于交错网格有限差分数值方法.
4 误差分析从算法的实现过程分析,计算的误差主要是:(1)算法误差,即时间层局部变化时,粗细网格过渡区域的插值计算误差;(2)离散误差,即速度场离散网格梯度变化导致的误差.
4.1 算法误差模型1为各向同性均匀介质,对模型1分别利用双变算法和普通交错网格算法模拟地震波在各向同性均匀介质中的传播.根据两种算法的结果来分析计算误差对算法精度的影响.表 1 为速度模型参数和模拟参数,子波类型均为主频为30 Hz的雷克子波.本文中对所有模型的数值模拟均采用了空间四阶差分精度、时间二阶差分精度的2D有限差分算法.
|
|
表 1 模型参数和正演模拟参数 Table 1 Model parameters and modeling parameters |
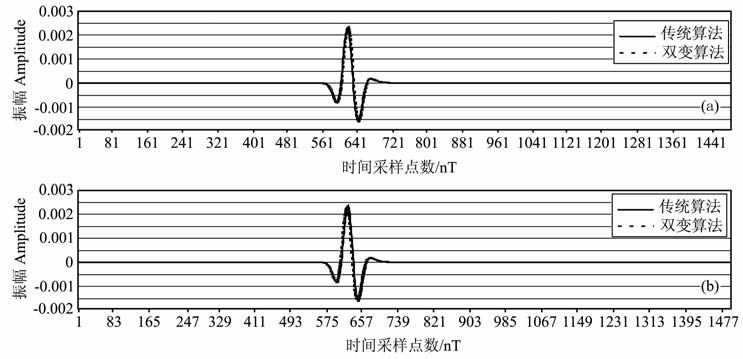
图 5为600ms时刻波场快照,从左到右依次为传统交错网格算法结果(全局采用大网格剖分)、双变交错网格算法结果和两种方法的对比结果.从图中可以看出采用双变算法得到的结果与传统算法得到的结果之间误差非常小.根据对600ms时刻波场快照记录的数据统计结果显示:x分量记录中,双变算法能量最大值为3.300134×10-3,传统交错网格算法结果能量最大值为3.300134×10-3,两种算法结果的最大差值为1.063186×10-5,相对误差为0.322%.z分量记录中,双变算法能量最大值为2.463512×10-3,传统交错网格算法结果能量最大值为2.463512×10-3,两种算法结果的最大差值为3.651634×10-6,相对误差为0.148%.因此可以得到结论:时间层内的插值算法带来的误差不是影响整体算法精度的关键因素,可以忽略.从两分量单道波形对比上(图 6)也可以看出,两种算法的结果从能量上和波形上都比较一致.由于采用的纵波震源,因此两分量记录的直达波结果差别较小.

|
图 5 600ms时刻波场快照(上:x分量;下:z分量) Fig. 5 Snapshot at 600 ms(top:xcomponent; bottom:z component) |
|
图 6 第51道波形对比(a, x分量;b, z分量) Fig. 6 Wavelet comparison of No.51 trace (a, x component; b, z component) |
在使用不规则网格时,网格步长不是随意变化的.在速度、密度等物性参数不变的情况下,网格步长的这种变化也可能会导致较强的人工数值反射.2003年SergioAdrianoMouraOliveira[15]首次对此进行了解释.即波场离散后相速度是网格步长的函数,当相速度变化较大时,即使速度和密度都没有变化,入射波的能量会部分反射回来,导致了数值反射现象.因为频散程度与频率有关,所以当入射波的频率较高时,数值反射现象较低频时高.
因此合理的选择网格变化梯度可以压制人工数值反射.在某些情况下,还可以对网格步长进行连续的变化,经过几次网格步长的变化调整到一定的步长范围.
5 稳定性条件双变算法中的全局时间采样不需要满足最短波长原则,同传统交错网格算法的稳定性条件是一致的[16].但是在全局时间层内,局部精细网格的时间计算步长需要满足局部最短波长原则.
影响双变算法稳定性的另外一个因素就是4.2节中提及的网格步长变化梯度.若是网格步长变化梯度比较剧烈,不仅会引起数值反射现象,造成计算误差.有时还会使计算溢出,无法运行.在地震勘探的空间采样范围内,米数量级网格步长的变化一般不会造成不稳定现象.若是空间网格出现跨数量级的步长变化,则需要平缓的、经过几次网格步长变化的处理来保证计算的稳定性.
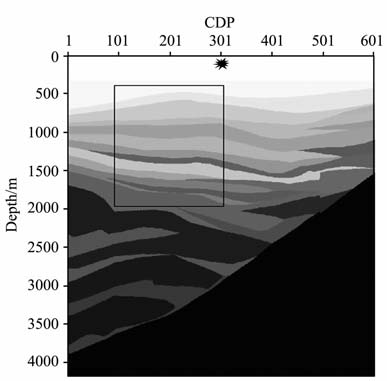
6 典型模型正演 6.1 复杂模型模型2是胜利油田某地区的局部陡坡带砂砾岩体速度模型(图 7).速度模型中部层位较多,层厚度较薄.因此对模型中部进行精细网格剖分,并采用样局部变时间算法进行正演模拟(矩形方框区域).模型参数和模拟参数如表 1.在大型集群master下对两种算法的耗时进行了对比,硬件环境为CPUSpeed2500 Hz, MemoryTotal8166004KB,SwapSpace Total16579072KB,采用传统算法(全局采用大网格剖分)单炮耗时为2104s, 采用双变算法单炮耗时为3150s.
|
图 7 陡坡带砂砾岩体速度模型 Fig. 7 Steep glutenite velocity model |
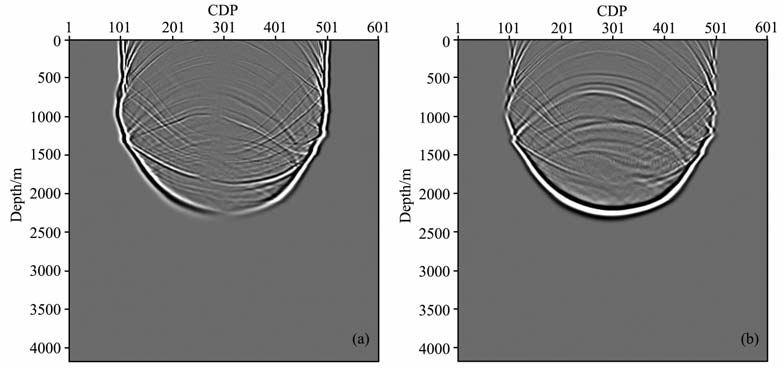
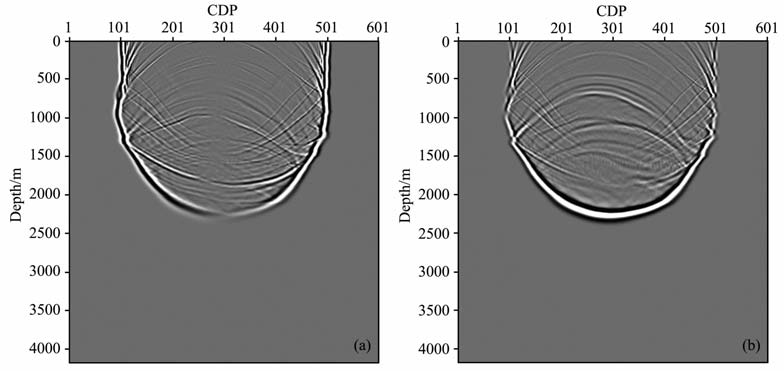
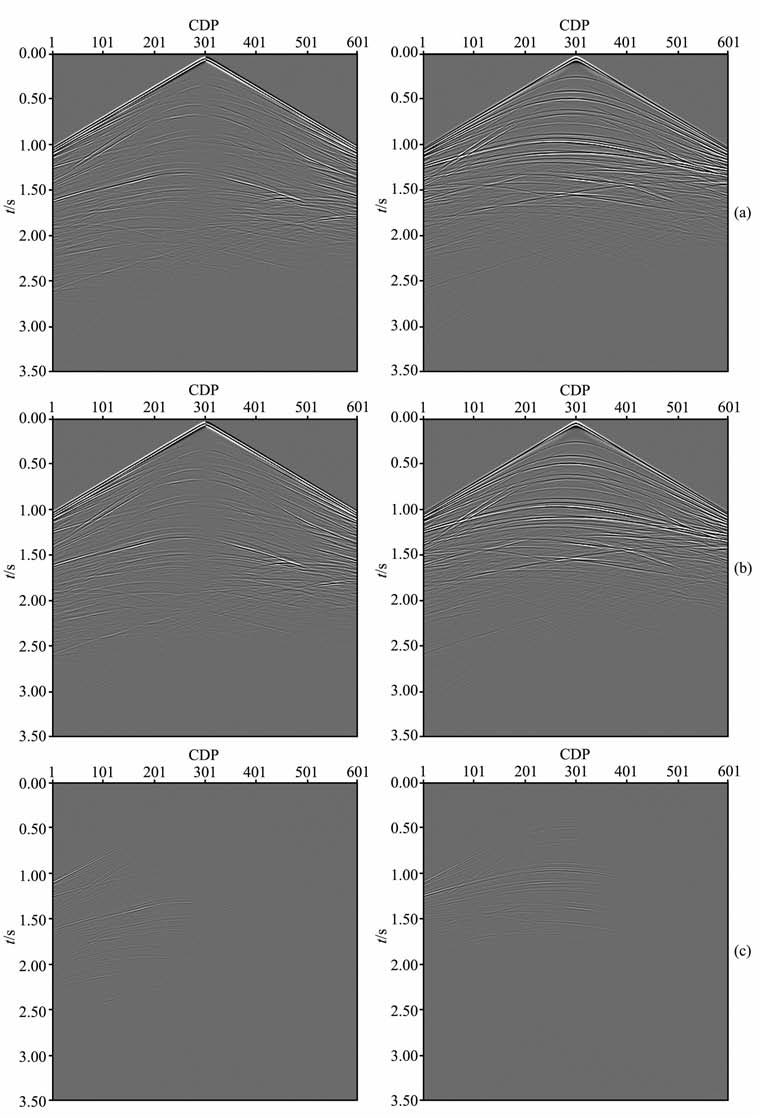
图 8是采用双变算法得到的1400ms时刻的水平方向波场快照(图 8a)和垂直方向波场快照(图 8b).图 9是采用传统算法得到的1400ms时刻的波场快照,图 9a是水平方向波场快照,图 9b是垂直方向波场快照.图 10a是采用双变算法得到的x分量和z分量的波场记录,图 10b是采用传统算法得到的x分量和z分量的波场记录,图 10c是两种方法的比较结果(均在相同增益下显示).
|
图 8 双变算法1400ms时刻波场快照(a, x分量;b, z分量) Fig. 8 Snapshot at 1400 ms of dua--variable method (a, x component; b, z component) |
|
图 9 传统算法1400ms时刻波场快照(a, x分量;b, z分量) Fig. 9 Snapshot at 1400 ms of traditional method (a, z component; b, z component) |
|
图 10 波场记录(左:x分量;右:z分量) (a)双变算法;(b)传统算法;(c)两种方法的比较结果. Fig. 10 Wavefield record (left:x component; right:z component) (a) Dual-variable method; (b) Traditional method; (c) Comparison result of two methods. |
从波场快照和炮记录上可以看出双变算法结果和传统结果算法能很好地吻合.从两种方法的对比结果上发现两种方法的主要不同是相位上的差别.出现这种差别的原因是正演模拟时数值频散主要是和网格间距有关,地震波相速度是网格步长的函数.在双变差分算法中,网格步长的变化也导致了地震波相速度的变化.有时尽管差别很小,但是这种相速度的变化仍然会使变网格算法的结果在一定的程度上同传统算法的结果存在差别.
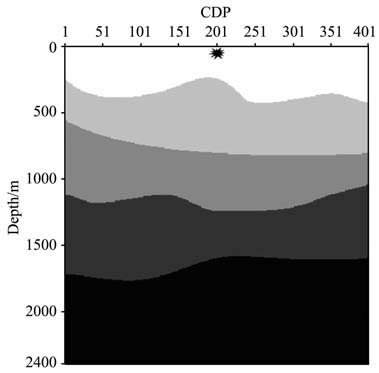
6.2 低降速带模型模型3是低降速带模型,表层为速度为867m/s的低速带(图 11).模型参数和模拟参数如表 1.针对本文中的模拟参数设置,空间采样hmax<3.33m.全局采用6m网格采样不能满足稳定性要求,因此对表层进行局部网格细分和局部变时间采样来保证计算的稳定性,同时又不增加过大的计算量.
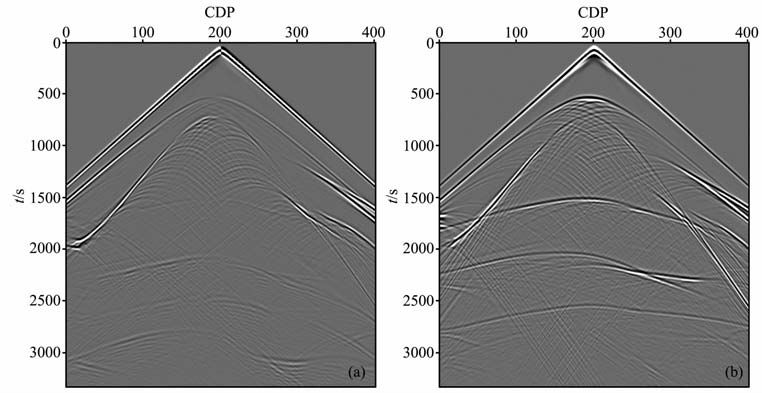
图 12为沿水平方向接收的波场记录和沿垂直方向接收的波场记录.从图中看出由于层界面起伏,用矩形网格离散速度场时,倾斜界面处会产生一系列阶梯状的毛刺,在模拟时产生大量的绕射噪声,对波场记录中的有效反射轴能量产生了压制作用.在界面处采用三角网格或更为精细的矩形网格,能更好地逼近界面,消除这种绕射噪声.从图中没有观察到通常情况下低速带造成的数值频散现象.
|
图 11 表层低速带速度模型 Fig. 11 Surface low-velocity model |
|
图 12 低速带速度模型波场记录(a, x分量;b, z分量) Fig. 12 Wavefield record of surface low-velocity model (a, z component; b, z component) |
从以上的模型测试结果和分析看出,局部变时间和局部变网格结合的算法(双变算法)能从根本上节约计算时间.对表层为低降速带的速度模型或内部存在低速层的速度模型在降低内存存储和计算量的同时,还能满足最短波长原则带来的稳定性问题.因此,对传统算法无法适应的一些复杂地质情况,双变算法能提供更好的解决思路.
双变算法中虽然加入了插值计算,但是计算区域集中计算量非常少.从对算法的误差分析中看出,算法本身引入的误差非常小,对整体的计算结果不会产生不稳定情况,也不影响整体计算结果的精度,可以忽略不计.应该注意的是模型网格剖分本身带来的误差影响,它可能会导致比较强的人工数值反射,严重时计算会溢出,计算无法进行.这种网格梯度变化带来的误差,可以通过合理地选择网格变化来避免,或者对网格步长变化采取连续变化的方式,在多个网格变化范围内达到需要的步长尺度.
| [1] | 杜世通. 地震波动力学. 山东东营: 石油大学出版社, 1999 . Du S T. Seismic Wave Dynamics (in Chinese). Shandong Dongying: China University of Petroleum Press, 1999 . |
| [2] | Jastram C, Behle A. Acoustic modeling on a vertically varying grid. Geophys. Prosp. , 1992, 40: 157-169. DOI:10.1111/gpr.1992.40.issue-2 |
| [3] | Jastram C, Tessmer E. Elastic modeling on a grid of vertically varying spacing. Geophys. Prosp. , 1994, 42: 357-370. DOI:10.1111/gpr.1994.42.issue-4 |
| [4] | Ivo Oprsal, Jiri Zahradnik. Elastic finite-difference method for irregular grids. Geophysics , 1999, 64: 240-250. DOI:10.1190/1.1444520 |
| [5] | Pitarka A. 3D elastic finite-difference modeling of seismic motion using staggered grids with nonuniform spacing. Bull. Seism. Soc. Am. , 1999, 89: 54-68. |
| [6] | Wang Y, Xu J, Schuster G T. Viscoelastic wave simulation in basins by a variable-grid finite-difference method. Bull. Seism. Soc. Am. , 2001, 91: 1741-1749. DOI:10.1785/0120000236 |
| [7] | Falk J, Tessmer E, Gajewski D. Efficient finite-difference modelling of seismic waves using locally adjustable time steps. Geophys. Prosp. , 1998, 46: 603-616. DOI:10.1046/j.1365-2478.1998.00110.x |
| [8] | Tessmer E. Seismic finite-difference modeling with spatially varying time steps. Geophysics , 2000, 65: 1290-1293. DOI:10.1190/1.1444820 |
| [9] | Hayashi K, Burns D R, Toksoz M N. Discontinuous-grid finite-difference seismic modeling including surface topography. Bull.Seism.Soc.Am. , 2001, 91: 1750-1764. DOI:10.1785/0120000024 |
| [10] | Virieux J. P-SV wave propagation in heterogeneous media: velocity-stress finite-difference method. Geophysics , 1986, 51: 88-901. |
| [11] | Graves R W. Simulating seismic wave propagation in 3D elastic media using staggered-grid finite-differences. Bull. Seism. Soc. Am. , 1996b, 86: 1091-1107. |
| [12] | Igel H, Riollet B, Mora P. Accuracy of staggered 3-D finite-difference grids for anisotropic wave propagation. SEG Expanded Abstracts, 1992. 1244~1246 |
| [13] | 董良国, 马在田, 曹景忠. 一阶弹性波方程交错网格高阶差分解法. 地球物理学报 , 2000, 43(3): 411–419. Dong L G, Ma Z T, Cao J Z. A staggered-grid high-order difference method of one-order elastic wave equation. Chinese J. Geophys. (in Chinese) , 2000, 43(3): 411-419. |
| [14] | 李振春, 张慧, 张华. 一阶弹性波方程的变网格高阶有限 差分数值模拟. 石油地球物理勘探 , 2008, 43(6): 711–716. Li Z C, Zhang H, Zhang H. Variable-grid high-order finite-difference numeric simulation of first-order elastic wave equation. Oil Geophysical Prospecting (in Chinese) , 2008, 43(6): 711-716. |
| [15] | Sergio Adriano Moura Oliveira. A fourth-order finite-difference method for the acoustic wave equation on irregular grids. Geophysics , 2003, 68: 672-676. DOI:10.1190/1.1567237 |
| [16] | 董良国, 马在田, 曹景忠. 一阶弹性波方程交错网格高阶差分解法稳定性分析. 地球物理学报 , 2000, 43(6): 856–864. Dong L G, Ma Z T, Cao J Z. A study of stability of the staggered-grid high-order difference method of one-order elastic wave equation. Chinese J. Geophys. (in Chinese) , 2000, 43(6): 856-864. |
 2011, Vol. 54
2011, Vol. 54


