地球物理学报  2011, Vol. 54 Issue (1): 6-13   PDF    
引用本文
丁留贯, 蒋勇, 李传起, 等. 同步轨道磁场和地面磁场对太阳风动压变化事件的响应. 地球物理学报, 2011, 54(1): 6-13, doi: 10.3969/j.issn.0001-5733.2011.01.002.  
DING L G, JIANG Y, LI C Q, et al. Response of geosynchronous magnetic field z component and geomagnetic field to solar wind dynamic pressure change. Chinese J. Geophys. (in Chinese), 2011, 54(1): 6-13, doi: 10.3969/j.issn.0001-5733.2011.01.002.  
同步轨道磁场和地面磁场对太阳风动压变化事件的响应
丁留贯1,2, 蒋勇1 , 李传起2,3, 于超1     
1. 南京信息工程大学数理学院,南京 210044;
2. 中国科学院空间天气学国家重点实验室,北京 100190;
3. 广西师范大学,桂林 541004
收稿日期 2010-07-12, 2010-09-23 收修定稿
基金项目: 中国科学院空间天气学国家重点实验室开放课题(08262DAA4S)资助
作者简介: 丁留贯,男,1979年生,在读博士,主要从事磁层物理、电离层物理研究.E-mail:dlg@nuist.edu.cn
通讯作者: 蒋 勇,男,教授、博士生导师,主要从事数值模拟、空间天气方面的研究.E-mail:jianguk@163.com
摘要: 本文对磁宁静时的123个动压变化事件(不包含激波事件)进行了统计研究.研究表明,在白天侧(9~15MLT)同步轨道磁场z分量对太阳风动压增大、减小事件具有较强的正响应,而在夜侧(21~3MLT)响应明显减弱,响应幅度具有明显的磁地方时分布.对动压增大事件的平均响应幅度在午前最大,而对动压减小事件的平均响应幅度在午后达到最大.在白天侧,同步轨道磁场z分量响应幅度与太阳风动压上下游均方差有较好的线性正相关,两者比值随磁地方时具有明显的分布变化;对于同样的动压变化白天侧响应明显强于夜侧.地磁指数SYM-H响应幅度对太阳风动压上下游均方差具有明显的依赖关系,统计结果显示磁层压缩较强时,两者相关性较好.在白天侧,地磁指数响应幅度与同步轨道磁场z分量响应幅度具有明显的线性相关,晨昏侧相关性减弱,夜侧无明显相关.
关键词: 太阳风动压      地球同步轨道      地磁指数SYM-H      磁场响应      磁层顶电流     
Response of geosynchronous magnetic field z component and geomagnetic field to solar wind dynamic pressure change
DING Liu-Guan1,2, JIANG Yong1, LI Chuan-Qi2,3, YU Chao1     
1. College of Math and Physics, Nanjing University of Information Science & Technology, Nanjing 210044, China;
2. State Key Laboratory of Space Weather, Chinese Academy of Sciences, Beijing 100190, China;
3. Guangxi Normal University, Guilin 541004, China
Abstract: In this paper, we study 123 solar wind dynamic pressure change events, not including interplanetary shocks, with statistical methods. The results indicate that the geosynchronous magnetic field z component presents strong positive response to solar wind dynamic pressure changes near the noon meridian. The amplitude of geosynchronous magnetic field response shows an obvious magnetic local time distribution in our analysis. The largest amplitude of geosynchronous magnetic field z component response to solar wind dynamic pressure increase events is found at the pre-noon region, and that to decrease events is found at post noon region. On the dayside, the amplitude of geosynchronous magnetic field z component has the best correlation with the square root of the solar wind dynamic pressure, especially near the sunspot region. To the same solar wind dynamic pressure changes, the response on the dayside is significantly stronger than that on the night-side, with distinguished magnetic local time distribution. The dependence between geomagnetic indices SYM-H response amplitude and the square root of the solar wind dynamic pressure is very distinct, especially when magnetosphere is strongly compressed. The amplitude of sudden impulses (dSYM-H) correlates better with the amplitude of magnetic field at geosynchronous orbit near the sub-solar region, which declines in the region of dawn and dusk, especially weakens near the midnight region.
Key words: Solar wind dynamic pressure      Geosynchronous orbit      Geomagnetic indices SYM-H      Response of magnetic field      Magnetopause current system     
1 引言

行星际太阳风动压经常发生大幅度快速变化，对应空间等离子体数密度或速度也通常发生大幅度快速变化，这已被多个观测数据所证实[1, 2].大而快的太阳风动压扰动作用于磁层顶时会引起磁层电离层电流的变化，如磁层顶电流(Chapman-Ferraro电流)、环电流、场向电流(Birkeland电流)和越尾电流等等.各个电流系对太阳风动压扰动的响应幅度及时间延迟通常不尽相同，并随磁地方时有明显变化.磁层电离层电流的扰动将引起地球磁场不同区域不同程度的扰动.同步轨道磁场和地面磁场通常是受磁层电流和电离层电流主要影响的典型研究对象.

Rufenach等人[3]通过对GOES 卫星所观测的同步轨道磁场的小时平均值数据进行分析，得出磁宁静条件下同步轨道磁场随太阳风动压的增加而增加.Wing等人[4]总结出了磁宁静时期同步轨道磁场各分量与太阳风动压及行星际磁场之间的统计关系式，他们得出磁层磁场变化与太阳风动压变化在白天侧具有正相关而在夜侧具有负相关，并指出“场向电流"可能是影响相关性晨昏不对称的一个因素.Wing等人[5]还对行星际磁场及动压变化引起的磁层同步轨道磁场响应的时间延迟进行分析，发现白天侧响应先于晨昏侧、夜侧，动压与磁层的相互作用具有明显的磁地方时分布.Borodkova等人[6]通过对Prognoz10及GOES卫星的数据进行分析，得出在地球白天侧同步轨道磁场主要受太阳风动压及前向激波影响，并给出对应的统计关系；同时还发现行星际磁场方向及大小的波动对同步轨道磁场也有影响.乐超等人[2]通过对GOES和LANL 卫星数据的分析表明，激波峰前到达同步轨道后，在白天扇区(8~16MLT)同步轨道总磁场有明显增强，同步轨道磁场GSM 坐标系下Bz分量与总磁场变化趋势非常一致，而By在激波到达同步轨道前后基本不发生变化.Wang 等人[7]通过对激波事件的统计研究，得出在白天侧(9~15MLT)同步轨道磁场与太阳风动压上下游均方差具有明显的正相关关系，这一结论与Borodkova等人[8]对动压事件的统计结果基本一致.

太阳风动压与磁层顶相互作用，引起电离层电流及环电流的明显变化，进而影响地球表面磁场.Wang等人[7]通过对地磁指数SYM-H 对激波事件的响应进行分析，表明在磁层中度压缩的情况下，地磁指数与太阳风动压上下游均方差具有较好的线性正相关.Wang等人[9]通过对1964~2001年Dst指数及太阳风动压对环电流衰退和注入情况进行研究，指出在行星际磁场南向时环电流的注入率正比于太阳风动压，并据此改善Dst指数的预报水平，尤其在强的地磁暴期间准确度更高.Russell等人[10, 11]分析了低纬地磁场水平分量对行星际激波的响应，结果表明磁层顶电流和越尾电流对地球地面磁场的响应同等重要.Le等人[12]对动压变化事件的分析得出，地磁水平分量对太阳风动压扰动的预响应为向阳侧早晨扇区呈现短暂的微弱的上升，下午扇区及夜侧为短暂下降，而主响应除了早晨扇区外趋于偶极型变化.Araki等人[13]通过研究Dst指数和地磁水平分量统计图包络线，得出在环电流很小情况下，地磁水平分量随太阳风动压增加而增加，但在动压较大时增加趋势有所减弱.此外，在对Dst指数进行预报时，考虑太阳风动压的影响，比仅考虑行星际晨昏电场时的预测结果要好[14].

本文将对太阳风动压事件进行统计分析，讨论同步轨道磁场z分量及地磁指数SYM-H 对太阳风动压扰动的响应.根据Wing等人[4]的结论，在磁宁静时，大的太阳风扰动对地球磁层磁场的影响主要依赖动压，对行星际磁场z分量依赖性较弱，故本文暂不考虑行星际磁场对响应的影响.

2 数据来源及分析

本文选取ACE 卫星太阳风等离子体数密度和速度数据、GOES卫星磁场数据、地磁指数SYM-H数据.太阳风等离子体数据来自ACE 卫星的SWE，数据时间分辨率为64s.GOES 卫星运行在同步轨道上，选用GOES8/10/11/12卫星的磁场数据及卫星位置，时间分辨率为60s.Dst指数是使用最广泛的描述磁暴活动强度的指数，它由4 个低纬度观测站所测量的地磁场水平分量扣除平静期平均变化并根据台站纬度做调整而得到[15]，时间分辨率为1h, 其大小是环电流强度的量度.SYM-H 指数是一种新的衡量环电流强度的地磁指数，是地磁场水平分量的对称扰动.与Dst指数相比，SYM-H 指数在获得数据的观测站及坐标系等方面略有不同，数据分辨率为1min, 可以看作是高分辨率的Dst指数[16].SYM-H 指数是从10 个几乎均匀分布于各个经度上的中低纬地磁台站中随机6个台站的磁场南北向分量平均值.地磁指数SYM-H 对太阳风动压扰动的响应可看成全球地磁台站对太阳风动压扰动响应的平均情况.

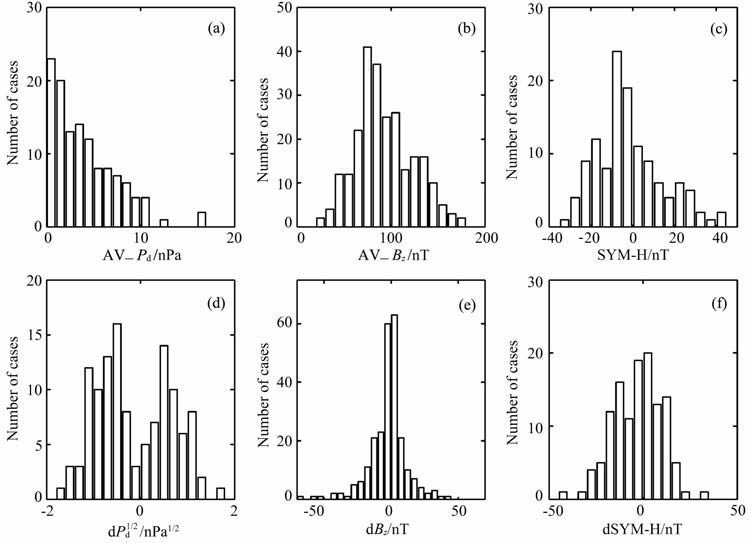
本文选择了2002~2008 年间123 个大的动压变化事件，选择依据为动压变化幅度大于扰动前太阳风动压的1倍，处于磁宁静时期(扰动前后各3h内满足Dst>-30nT).在这123个动压变化事件中，动压增大事件占54个(不包含激波事件)，动压减小事件占69个.本文所选动压变化事件统计直方图如图 1所示.图 1(a~c)分别为太阳风动压扰动前30min动压平均值、扰动前30 min同步轨道磁场Bz分量(GSM 坐标)平均值、地磁指数SYM-H 扰动前上游值的统计直方图.图中显示动压平均值主要集中在11nPa以下，同步轨道磁场z分量平均值主要集中在50~150nT 之间，地磁指数SYM-H 上游值主要集中在-30~ +40nT之间，所有数据基本呈正态分布，符合统计规律.图 1(d~f)分别为太阳风动压上下游均方差幅度、同步轨道磁场z分量响应幅度及地磁指数SYM-H 响应幅度.动压上下游均方差具有双峰特点，最大概率分别出现在-0.5nPa1/2、+0.5nPa1/2附近，可近似看成动压增加事件、动压减小事件各自正态分布的叠加.同步轨道磁场响应幅度及地磁指数SYM-H 响应幅度均呈现关于原点对称的正态分布.

图 1 太阳风动压变化事件数据统计直方图 Fig. 1 Histogram of solar wind dynamic pressure events
3 个例分析

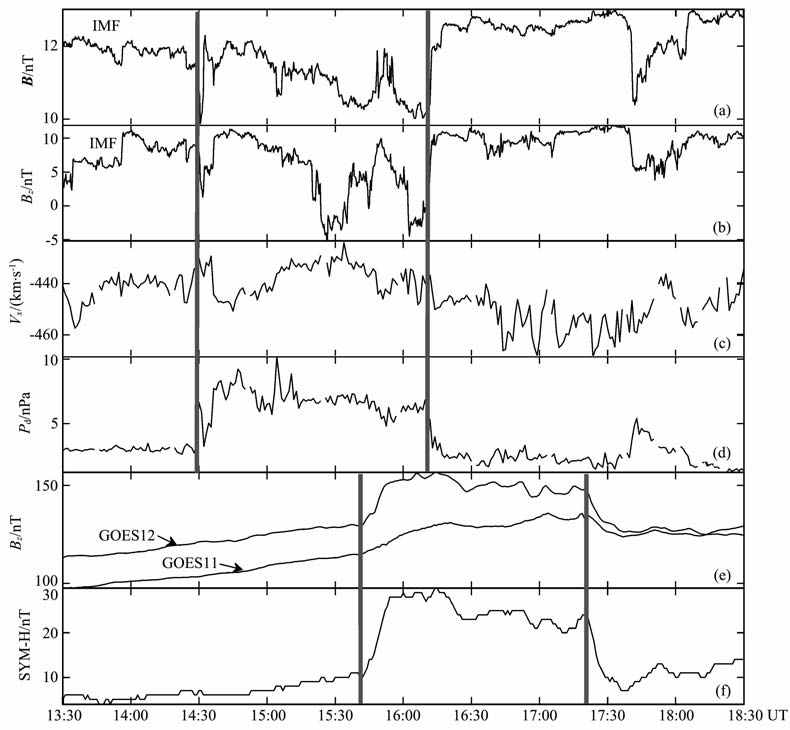
图 2为一个典型的动压扰动事件.图 2(a~d)显示了2008年9月3日ACE卫星在L1点观测到的太阳风数据.在14∶30UT，太阳风动压Pd 从3nPa快速增加到6.6nPa, 等离子体数密度(图中未画出)出现了明显的增强，扰动前太阳风x方向(GSE 坐标系)速度分量大约为440km/s, 假设太阳风速度在此后向地球传播过程中保持不变，则从L1点经过大约53 min到达地球磁层顶与地球磁层作用.图 2(e, f)显示了在太阳风动压扰动前后一段时间内由GOES11和GOES12探测到的GSM 坐标系下地球同步轨道磁场z分量及地磁指数SYM-H 的变化.从图中可以看出，在15∶40UT 同步轨道磁场和地磁指数几乎同时出现了突然增强，这可以认为是磁层磁场和地面磁场对14∶30UT ACE 卫星观测到的动压增加事件的响应，这一响应时刻落后L1点的动压扰动时刻大约70 min.实际时延与计算值存在17min的差异，可能原因是太阳风传播过程中速度发生了较大变化.从图 2 中还可以看出，在16∶10UT ACE 卫星又探测到一个动压减小事件，随后在17∶20UT 同步轨道磁场及地磁指数产生了快速的下降，此响应时间延迟也为70 min.从这个事例可以明显看出，同步轨道磁场z分量及地磁指数SYM-H 对行星际太阳风动压的剧烈扰动具有明显的正响应.地磁指数SYM-H 响应幅度较为显著，同步轨道磁场响应幅度则与GOES卫星位置有关.图 2中GOES12卫星所探测到的响应较明显，此时 GOES12处在10∶40MLT(正午附近)，而GOES11卫星探测到的响应较弱，此时GOES11处在06∶40MLT(晨侧).总体而言，白天侧正午附近磁层磁场对太阳风动压响应较强，在其他区域相对较弱.

图 2 2008年9月3日太阳风动压扰动事件 Fig. 2 An example of response of geosynchronous magnetic field z component and magnetic indices caused by solar wind dynamic pressure change on 3 September 2008
4 统计分析 4.1 同步轨道磁场z分量对太阳风动压扰动的响应

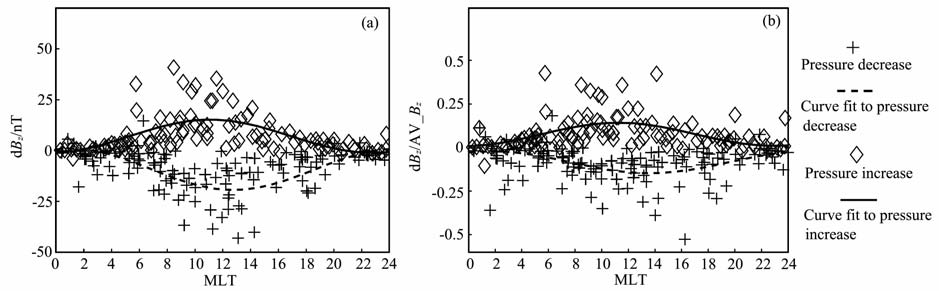
图 3显示了同步轨道磁场z分量响应幅度dBz(取动压扰动到达同步轨道之后的第一个波峰作为下游磁场值，动压扰动到达前一刻的磁场值作为上游值[17, 18]，dBz由上下游磁场z分量计算得到)及相对响应幅度dBz/AV_Bz(其中AV_Bz为磁场扰动前30min的平均场强)随磁地方时的分布.由图 3a可以看出，在磁地方时正午附近，同步轨道磁场对太阳风动压扰动响应的幅度相对较大，在午夜附近区域响应幅度相对较小，有时还会出现零响应或负响应，这与Wang[7]、Borodkova[9]及Lee[19]等人的统计结果基本一致.图中实线为同步轨道磁场对动压增大事件的平均响应幅度的拟合曲线，虚线为动压减小事件的平均响应幅度的拟合曲线.从拟合曲线来看，同步轨道磁场响应幅度在白天侧大于夜侧，并在午夜附近达到最小，且有时出现微弱的负响应.对于动压增大事件的平均响应幅度最大值出现在午前11 时附近，这一点与Sibeck等人[20]的结论一致；动压减小事件的平均响应幅度最大值出现在午后13 时附近，增大事件、减小事件响应的磁地方时分布关于子午面近似对称.另外，相对响应幅度对磁地方时的依赖性(图 3b)相比绝对响应幅度(图 3a)而言有所减弱，平均幅度最大仅0.15.

图 3 同步轨道磁场z分量响应幅度dBz(a)及相对响应幅度dBz/AV_Bz(b)对磁地方时的依赖关系 Fig. 3 Dependence of (a) the amplitude dBz and (b) the relative amplitude Bz/AV_Bz of geosynchronous magnetic field response on magnetic local time

图 4给出了同步轨道磁场z分量响应幅度与扰动前平均场强的关系，虚线是拟合曲线.由图可以看出，磁场响应幅度总体上随扰动前平均场强的增加而增加.由拟合曲线可知相对响应幅度在磁场较弱时较小且随平均场强变化不大，在磁场较强时则相对响应幅度明显增加.

图 4 同步轨道磁场响应幅度与扰动前平均场的相关关系 Fig. 4 The relationship between amplitude of geosynchronous magnetic field and AV_Bz

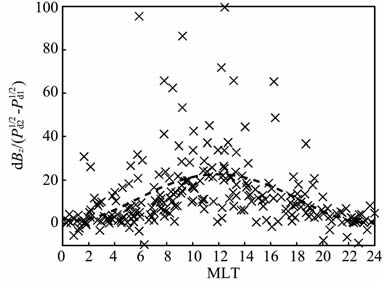
太阳风动压扰动作用于磁层顶，引起磁层顶电流变化，白天侧(9~15MLT)的磁层磁场扰动主要受磁层顶电流控制[21~23]，这一区域的同步轨道磁场对太阳风动压扰动具有较强的响应.图 5 显示了在白天侧同步轨道磁场z分量与太阳风动压上下游均方差(Pd1为太阳风扰动上游动压值，Pd2为下游动压值)的关系，虚线是拟合曲线.从数据的分布来看，两者具有很好的线性相关关系，相关系数达到0.84.同步轨道磁场对太阳风动压扰动呈现较强的正响应，这也进一步说明白天侧磁层磁场主要受磁层顶电流影响，这一点与Wang[7]和Borodkova[8]等人的结论一致.在晨昏侧(3~9MLT，15~21MLT)、夜侧(21~3MLT)两者的相关性明显下降(限于篇幅，图未给出)，说明在这些区域磁层磁场可能还受场向电流、越尾电流等的影响，情况比白天侧复杂.图 6给出了同步轨道磁场z分量响应幅度对太阳风动压上下游均方差比值随地方时的变化，虚线是平均效果的拟合曲线.从图中大致可以看出，对于同样的动压变化，同步轨道磁场z分量对太阳风动压扰动的响应在正午(12MLT)附近最强，在午夜(0MLT)附近最弱，接近零响应(主要因为午夜附近受越尾电流的影响较大).

图 5 白天侧(9＜MLT＜15)同步轨道磁场响应幅度与太阳风动压上下游均方差的相关关系 Fig. 5 Dependence of the change of geosynchronous magnetic field (dBz)from 09 :00 to 15 :00MLT on the change of the square root of the solar wind dynamic pressure
图 6 同步轨道磁场响应幅度与太阳风动压上下游均方差比值对磁地方时的依赖关系 Fig. 6 Dependence of the ratio dBz/(Pd21/2 -P d11/2)of geosynchronous magnetic field on magnetic local time
4.2 地磁指数SYM-H 对太阳风动压扰动的响应

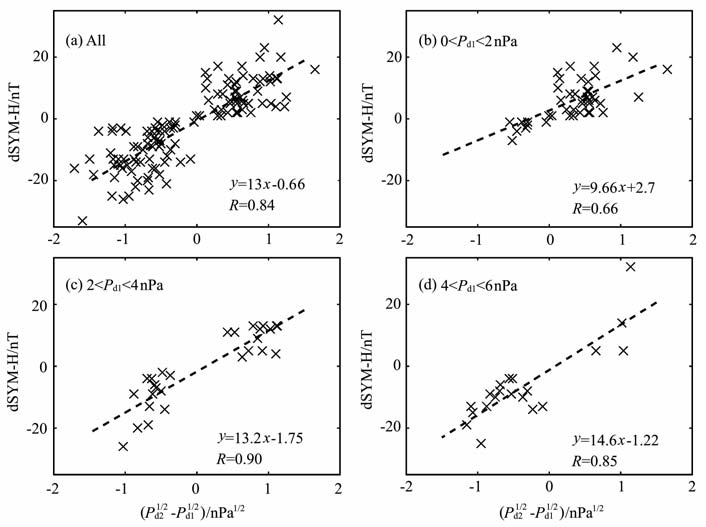
由图 2 可以看出，地磁指数SYM-H 对太阳风动压扰动的响应比较明显，这说明太阳风动压扰动作用于磁层顶同样引起了环电流、电离层电流的显著变化.图 7给出了地磁指数SYM-H 响应幅度与太阳风动压上下游均方差的统计关系.图 7a呈现了所有事件的统计结果，线性相关系数达到0.84，具有较显著的线性正相关，这与Araki等人[13]的结论相符.同时也说明SYM-H指数对太阳风动压有很强的依赖关系.基于上游太阳风动压值，大致将事件分为三组:0 ＜Pd1＜2nPa(图 7b)、2＜Pd1＜4nPa(图 7c)、4＜Pd1＜6nPa(图 7d)，图中虚线为拟合曲线.从相关系数可以看出，当磁层具有较大程度压缩时，地磁指数SYM-H 响应幅度与太阳风动压上下游均方差线性相关性较好.

图 7 地磁指数SYM-H 响应幅度与太阳风动压上下游均方差的相关关系 Fig. 7 Dependence of the amplitude of sudden impulses dSYM-H on the change of the square root of the solar wind dynamic pressure in quiet time
4.3 地磁指数SYM-H 响应幅度与同步轨道磁场z分量响应幅度的关系

影响SYM-H 指数变化的因素除了磁层电流以外，还有电离层电流，而同步轨道在电离层之上，可以认为对同步轨道磁场影响的主要因素为磁层电流由于在同步轨道的不同区域，影响同步轨道磁场的电流有所不同，为方便分析，将同步轨道分成4个不同区域:白天侧(9~15MLT)、昏侧(15~21MLT)、晨侧(3~9MLT)、夜侧(21~3MLT)，比较各个区域同步轨道磁场z分量响应幅度与地磁指数SYM-H 响应幅度之间的关系.

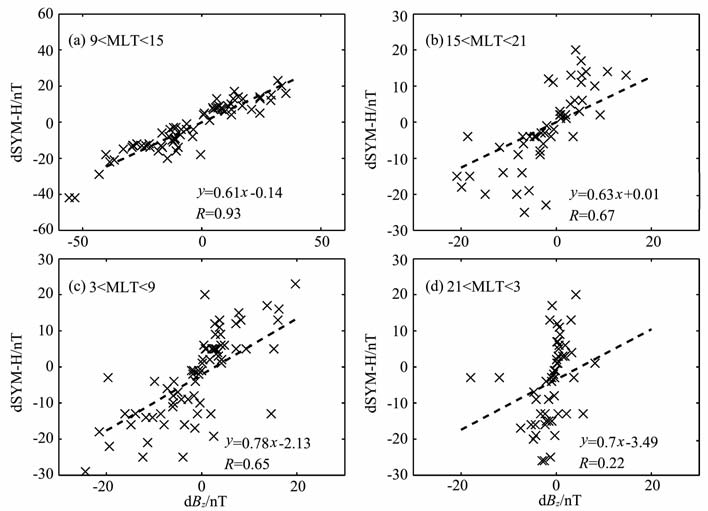
图 8给出了比较结果.在白天侧，同步轨道磁场响应幅度与地磁指数响应幅度具有很好线性关系，相关系数达到0.93.由于白天侧同步轨道磁场响应主要来自磁层顶电流的变化，可以认为地磁指数 SYM-H 对动压事件的响应也主要来自磁层顶电流的影响.从图 8(b~d)可以看出，地磁指数响应幅度 dSYM-H 与同步轨道响应幅度dBz的相关系数在晨昏侧大致相同，而在夜侧相关性最差.在晨昏侧及夜侧相关性不高说明影响这些区域的电流系较白天侧复杂，不仅仅有磁层顶电流，可能还有场向电流、越尾电流.

图 8 地磁指数响应幅度与同步轨道磁场响应幅度相关关系 Fig. 8 Relationship between the amplitude of sudden impulses dSYM-H and the geosynchronous magnetic field responses dBz in the regions of (a) sub-solar, (b) dusk, (c) dawn, and (d) midnight
5 结论

(1) 太阳风动压扰动作用于磁层顶引起磁层、电离层电流的强烈扰动，进而影响磁层磁场及地面磁场；统计显示，同步轨道磁场z分量及地磁指数 SYM-H 呈现明显的响应，白天侧响应较夜侧强烈.

(2) 同步轨道磁场z分量对动压增大、减小事件的响应近似关于子午面对称，具有明显的磁地方时分布；平均响应幅度最大值出现在磁地方时11时和13时附近；相对响应幅度随磁地方时分布的差异不大，并大致随扰动前平均场强的增加而增加.

(3) 在白天侧，同步轨道磁场响应幅度与太阳风动压上下游均方差具有很好的线性相关，这说明白天侧同步轨道磁场主要受磁层顶电流影响.

(4) 统计结果显示，地磁指数SYM-H 响应幅度与太阳风动压上下游均方差具有较好的线性相关关系；同时还指出在磁层具有较大程度压缩的情况下，两者相关性更好.

(5) 地磁指数SYM-H 响应幅度与同步轨道磁场z分量响应幅度在白天侧具有很好的线性相关关系，在晨昏侧具有类似的线性相关关系，但相关系数较白天侧要小，夜侧不具有明显的线性相关关系.这可说明影响晨昏侧、夜侧同步轨道磁场和地面磁场的电流较白天侧更复杂.

作者接下来的工作是将以上的结论在MHD(MagnetoHydroDynamic, 磁流体)数值模拟中进行验证，并进一步说明其中的物理机制.

致谢

感谢http://spdf.gsfc.nasa.gov/提供太阳风数据及同步轨道磁场数据及日本京都世界数据中心 http://swdcwww.kugi.kyoto-u.ac.jp/提供的地磁指数.

参考文献
[1] Bowe G A, Hapgood M A, Lockwood M, et al. Short-term variability of solar wind number density, speed and dynamic pressure as a function of the interplanetary magnetic field components: a survey over two solar cycles. Geophys. Res. Lett. , 1990, 17(11): 1825-1828. DOI:10.1029/GL017i011p01825
[2] 乐超, 宗秋刚, 王永福. 地球同步轨道磁场和等离子体行为对行星际激波的响应. 科学通报 , 2009, 54(18): 2835–2843. Yue C, Zong Q G, Wang Y F. Response of the magnetic field and plasmas at the geosynchronous orbit to interplanetary shock. Chinese Sci. Bull. (in Chinese) , 2009, 54(18): 2835-2843.
[3] Rufenach C L, McPherron R L, Schaper J. The quiet geomagnetic field at geosynchronous orbit and its dependence on solar wind dynamic pressure. J. Geophys. Res. , 1992, 97: 25-42. DOI:10.1029/91JA02135
[4] Wing S, Sibeck D G. Effects of interplanetary magnetic field z component and the solar wind dynamic pressure on the geosynchronous magnetic field. J. Geophys. Res. , 1997, 102: 7207-7216. DOI:10.1029/97JA00150
[5] Wing S, Sibeck D G, Wiltberger M, et al. Geosynchronous magnetic field temporal response to solar wind and IMF variations. J. Geophys.Res. , 2002, 107(A8): 1222.
[6] Borodkova N L, Zastenker G N, Sibeck D G. A case and statistical study of transient magnetic field events at geosynchronous orbit and their solar wind origin. J. Geophys. Res. , 1995, 100: 5643-5656. DOI:10.1029/94JA03144
[7] Wang C, Liu J B, Li H. Geospace magnetic field response to interplanetary shocks. J. Geophys. Res. , 2008, 114: A02511.
[8] Borodkova N L, Liu J B, Huang Z H, et al. Geosynchronous magnetic field response to large and fast solar wind dynamic pressure change. Advances in Space Research , 2008, 41(8): 1220-1225. DOI:10.1016/j.asr.2007.05.075
[9] Wang C B, Chao J K, Lin C H. Influence of the solar wind dynamic pressure on the decay and injection of the ring current. J. Geophys. Res. , 2003, 108(A9): 1341. DOI:10.1029/2003JA009851
[10] Russell C T, Ginskey M. Sudden impulses at low latitudes: transient response. Geophys. Res. Lett. , 1993, 20(11): 1015-1018. DOI:10.1029/93GL01257
[11] Russell C T, Ginskey M, Petrinec S M. Sudden impulses at low-latitude stations: steady state response for northward interplanetary magnetic field. Geophys. Res. Lett. , 1994, 99(A1): 253-261. DOI:10.1029/93JA02288
[12] Le G, Russell C T, Petrinec S M, et al. Effect of sudden solar wind dynamic pressure changes at subauroral latitudes: change in magnetic field. J. Geophys. Res. , 1993, 98(A3): 3983-3990. DOI:10.1029/92JA02397
[13] Araki T, Funato K, Iguchi T, et al. Direct detection of solar wind dynamic pressure effect on ground geomagnetic field. Geophys.. Res. Lett. , 1993, 20(9): 775-778. DOI:10.1029/93GL00852
[14] Xie H, Gopalswamy N, Cyr O C St, et al. Effects of solar wind dynamic pressure and preconditioning on large geomagnetic storms. Geophys. Res. Lett. , 2008, 35: L06S08.
[15] Mayaud P N. Derivation, Meaning, and Use of Geomagnetic Indices. Geophysical Monograph 22. Washington: American Geophysical Union, 1980 .
[16] Wanliss J A, Showalter K M. High-resolution global storm index: Dst versus SYM-H. J. Geophys. Res. , 2006, 111: A02202.
[17] Zhang X Y, Zong Q G, Wang Y F, et al. ULF waves excited by negative/positive solar wind dynamic pressure impulses at geosynchronous orbit. J. Geophys. Res. , 2010, 115: A10221. DOI:10.1029/2009JA015016
[18] Zong Q G, Zhou X Z, Wang Y F, et al. Energetic electron response to ULF waves induced by interplanetary shocks in the outer radiation belt. J. Geophys. Res. , 2009, 114: A10204.
[19] Lee D Y, Lyons L R. Geosynchronous magnetic field response to solar wind dynamic pressure pulse. J. Geophys. Res. , 2004, 109: A04201.
[20] Sibeck D G. A model for the transient magnetospheric response to sudden solar wind dynamic pressure variations. J. Geophys. Res. , 1990, 95(A4): 3755-3771. DOI:10.1029/JA095iA04p03755
[21] Kivelson M G, Russell C T. Introduction to Space Physics. Cambridge: Cambridge University Press, 1995 : 227 -232.
[22] Ostapenko A A, Maltsev Y P. Three-dimensional magnetospheric response to variations in the solar wind dynamic pressure. J. Geophys. Res. , 1998, 25(3): 261-263.
[23] Borodkova N L, Zastenker G N, Riazantseva M, et al. Large and sharp solar wind dynamic pressure variations as a source of geomagnetic field disturbances at the geosynchronous orbit. Planet. Space Sci. , 2005, 53: 25-32. DOI:10.1016/j.pss.2004.09.025