雷电作为低层大气一种常见的自然灾害源,出现频率极高.其大电流、强冲击波和瞬变电磁场对电力、能源、通信、交通、航空航天、国防及人身安全等造成了重大的威胁,因此雷电防护一直是电磁防护领域一项重要而困难的课题[1~4].完善现有防雷措施并开展新型防雷理论与技术研究,有必要对雷电监测技术和雷云荷电结构进行深入探索,利用地面电场观测数据进行雷云荷电模型反演是一个可行的途径.所谓地球物理学反演问题,就是实现从地球物理异常(或响应)到地球物理模型映射的过程[5].由于实际反演问题的目标函数一般都是高度非线性的,因此传统的线性反演方法往往显得无能为力,雷云荷电模型反演同样无法回避这个问题.一些基于智能优化算法的非线性反演方法表现出对此类问题很好的适应性,但传统智能优化算法本身也存在一些效率和准确度问题.近十几年量子计算与智能优化算法相结合发展起来的量子优化方法使原始算法效能有了很大改进[6],成为地球物理反演发展的新方向.本文尝试利用比较成熟的几种量子反演方法,对雷云荷电模型进行反演研究.
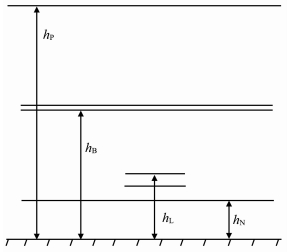
2 反演模型Amoruso和Lattarulo(2002)提出的雷云三层带电圆盘模型克服了以往偶极子模型过于简化的缺点,同时此模型给出的解析表达式受源电荷分布不均匀性影响较小[7, 8],用其描述雷云电场合理且简便,本文考虑对其进行反演.图 1为三层带电圆盘模型示意图.
|
图 1 三层带电圆盘模型示意图 Fig. 1 Three-layer charged disk model |
模型假设雷云中典型的从上到下正负正三级荷电结构可以用相应极性的带电圆盘来模拟.空间中的总场描述为[7]
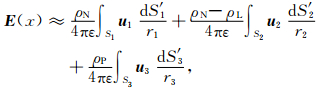
|
(1) |
其中ρN、ρL、ρP分别为负电荷堆、下部小型正电荷堆和上部正电荷堆的体电荷密度;u1、u2、u3分别为相应圆盘边界的单位法向矢量.
考虑大地的镜像作用,式(1)中的各项面积分可描述为[9]
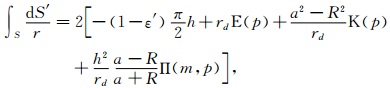
|
(2) |
其中K、E、Π分别为勒让德第一、二、三类完全椭圆积分[9, 10].a为雷云半径,R为地面距雷云中心的水平距离,h为带电圆盘垂直高度,rd=[(a+R)2 + h2]1/2,p=2(aR)1/2/rd,m=2(aR)1/2/(a+R),当R小于、等于或大于a时,ε′分别为-1,0,1.通过修改模型参数可得到不同尺度的雷云模型.
模型反演的目的是使地面电场的理论计算值与观测数据相吻合,依据最小二乘准则取反演目标函数为
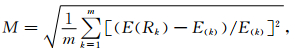
|
(3) |
即理论值与观测值的平均相对残差.其中E(k)为地面场强观测结果,总共有m个观测值,E(Rk)为相应观测点的模型计算值.
反演模型可描述为
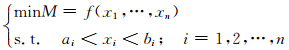
|
(4) |
其中xi为模型参数,具体为电荷密度ρN、ρL、ρP(单位nC·m-3),圆盘高度hp、hN、hL、hB(偶极层)和圆盘半径a、aL(单位m).ai、bi为解空间的边界.
不同的反演方法即确定具体的解空间搜索原则,使目标函数趋于极小值,得到模型参数的近似最优解.这些方法的设计要兼顾搜索效率、解的全局最优性与稳定性.
3 量子反演理论量子反演理论是量子计算与传统非线性反演方法相结合的产物[11, 12].近年一些实验显示经典智能优化算法的量子化在很大程度上加速了原算法并提高了其最优搜索能力[6, 13~22].这主要因为基于量子比特的编码方式使状态变量处于相干叠加态,从而极大地扩充了编码信息量并保证了解群体的多样性;用量子门(幺正算符)对态矢进行操作具有保持内积不变和均衡全局与局部搜索能力的优点;隧道效应与纠缠作用使一些算法在量子化后具有经典算法所不具备的搜索特征[6, 11, 12].因此,研究应用量子优化算法进行模型反演已经成为地球物理反演理论的发展趋势.本文主要对近年来发展比较成熟的三种量子反演方法进行总结分析.
3.1 量子遗传算法 3.1.1 量子遗传算法的基本原理经典遗传算法(Genetic Algorithm)将自然界遗传机制和生物进化原理引入参数编码形成的串联群体中,依目标函数通过交叉与变异操作对个体进行筛选,使优势个体保存下来,组成新群体,通过迭代,群体适应度不断提高.GA具有并行性、启发性和全局寻优的特点,同时也存在易早熟,后期收敛太慢的不足.基此,各国学者进行了大量的算法改进,量子化是最成功的途径之一.
K.H.Han(2000)把量子比特(二维相干态)引入遗传编码,并使用量子旋转门对量子编码的染色体进行幺正操作,通过观测使量子比特塌缩为经典比特,从而形成了现代意义上的量子遗传算法(Quantum Genetic Algorithm)[13, 14].此后十年,国内外以K.H.Han的算法为基础的各种改进的QGA大量涌现[6, 15, 16].文献[23]在K.H.Han思想基础上提出了基于Bloch坐标的QGA(BQGA),用量子比特构成染色体,用Bloch坐标描述染色体上的基因,直接用基因对参数编码,用量子旋转门进行染色体的更新,用量子非门进行染色体变异,避免了观测操作可能引起的随机退化,在缩小群体规模和提高收敛速度方面较原始QGA更有优势.
3.1.2 量子遗传算法反演的步骤(1)初始化.根据具体问题的复杂性来确定染色体群体的规模、变异率、量子旋转门转角、相对残差收敛参考值和最大进化代数.依所设定规模随机生成初始群体(染色体和基因用量子比特的Bloch坐标表示)[23].
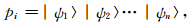
|
(5) |
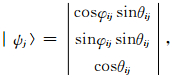
|
(6) |
其中pi为染色体,n为反演参数规模,式(6)为量子比特的Bloch坐标表示,每个染色体中有三条基因链.由初始群体经解码后可计算初始目标函数,得初始最优解和最优染色体.
(2)更新染色体.用量子旋转门对当代染色体中的每个量子比特进行么正操作,操作的原则是使每个染色体都趋向于当代最优染色体.
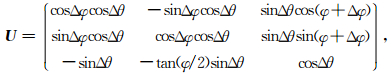
|
(7) |
U为Bloch坐标表示的量子旋转门[6],Δθ、Δφ为相应的转角,转角方向保证趋向当代最优解.关于确定转角的详细理论可参见文献[23].
为增强群体的多样性,可以生成伪随机数,若其大于变异率且考虑对象不是历史最优解时,利用量子非门对相应的量子比特进行操作.
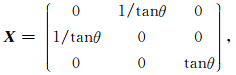
|
(8) |
X为量子非门的Bloch坐标表示[6].
(3)解码.当得到一个新的群体后,将每条基因链解码,得到相应的模型参数为
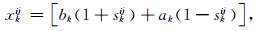
|
(9) |
skij为第i个染色体第j条基因链上对应第k个量子比特的Bloch坐标.
(4)计算目标函数.利用式(3)计算目标函数得到平均相对残差.
(5)评价.依据平均相对残差最小的原则筛选当代最优解和最优目标函数值并与历史最优解相比较,更新.当平均相对残差大于收敛参考值且迭代未达最大进化代数时,返回第(2)步循环.
3.2 量子退火算法 3.2.1 量子退火算法的基本原理不同于经典模拟退火算法(Simulated Annealing Algorithm)利用热波动来进行寻优,量子退火算法利用量子波动产生的隧道效应来实现全局优化[17].
一个量子系统态矢的演化由薛定谔方程描述
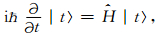
|
(10) |
其中ħ为约化普朗克常量,Ĥ为Hamilton算符,由动能项和势能项组成,
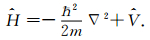
|
(11) |
考虑在一个随时间衰减的外扰场影响下,系统会发生跃迁,最终(理想状态)停留在势能最小状态(基态)下.将目标函数映射为系统势能,将模型参数映射为态矢自由度,通过计算跃迁振幅得到模型参数状态转移概率,模拟系统向基态跃迁的过程,这就是量子退火的基本思想.但当自由度很大时直接求解薛定谔方程是很困难的,所以量子退火一般通过蒙特卡罗方法来实现,包括路径积分蒙特卡罗(PQA)、格林函数蒙特卡罗、扩散蒙特卡罗和变分蒙特卡罗等[17~20],路径积分是其中应用较广的一种方法,文献[24]将其成功应用于大地电磁反演.
3.2.2 量子退火算法反演的步骤(1)初始化.根据具体问题复杂性确定扰动场Γ=Γ0β t(初始扰动场Γ0足够大,扰动衰减系数0<β<1),随机势垒阈值V0,相对残差收敛参考值ess,最大迭代次数T,邻域搜索次数l和各参数的搜索步长阈值μi.随机生成初始模型参数{x i(0) },计算初始目标函数M(0)[24].
(2)邻域搜索.对各参数依相应的步长阈值进行邻域搜索,并计算搜索的目标函数.搜索法则为
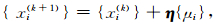
|
(12) |
其中η为区间[-1, 1]之间的随机数向量.
以扰动场Γ作为动能项,目标函数差值ΔM=M(k+1) -M(k)作为势能项,建立系统Hamilton量.
(3)计算传播子.引入演化算符Û(t,t0),由其定义可得|t〉=Û |t0〉,将态矢|t〉在x表象中展开可得[25]
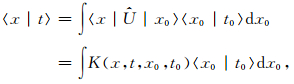
|
(13) |
其中核函数K称为传播子,它是|t0,x0〉到|t,x〉的跃迁振幅,即

|
(14) |
Feynman提出了计算K的路径积分方法,他假设跃迁振幅等于连接x0和x两点的所有路径贡献之和,而每条路径的贡献由其作用量决定[25],即
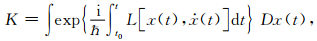
|
(15) |
其中L为Lagrange量,K表示为路径x(t)的泛函.
微元跃迁作用量与路径无关[25],传播子为
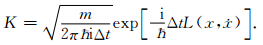
|
(16) |
对式(15)以折代曲用无穷个微元跃迁逼近可得与式(16)相似的结果.
考虑具体的反演问题,迭代时间间隔一定,因此式(16)中各项系数均为常量,模型参数的状态转移概率可以构造为
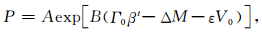
|
(17) |
其中A、B为常量,ε为区间[0, 1]内的随机数.每次邻域搜索后计算ΔM,若其小于0,更新模型参数,否则计算P,依概率随机决定是否更新参数.每次循环都要进行l次邻域搜索内循环以保证搜索质量.
(4)评价.记录当次循环的目标函数值,当平均相对残差大于收敛参考值ess且迭代未达最大迭代次数T时,返回第(2)步循环.
3.3 量子粒子群算法 3.3.1 量子粒子群算法的基本原理粒子群算法(Particle Swarm Optimization)是一种模拟群体行为的启发式优化方法.考虑粒子群中的每个粒子在解空间中以一定的速度飞行,搜索时兼顾自身历史最优搜索结果和群体历史最优搜索结果来调整搜索状态以达到整体寻优的目的.粒子状态的更新法则一般为[6]
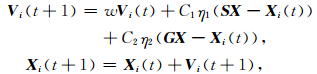
|
(18) |
其中V为粒子速度,X为粒子坐标即问题的解,w为惯性因子,C为自身和群体因子,η为随机数,SX为自身历史最优解,GX为群体历史最优解.
PSO的量子化采用了与GA量子化相同的思路.用量子比特编码,用量子旋转门进行幺正操作,旋转角由式(18)确定,用Pauli-X门进行突变处理,通过观测使量子比特塌缩为经典比特[26].
3.3.2 量子粒子群算法反演的步骤(1)初始化.根据具体问题的复杂性来确定粒子群规模、突变率、初始旋转角、惯性因子、自身和群体因子、相对残差收敛参考值和最大迭代次数.依所设定规模随机生成初始群体.
(2)更新粒子状态.根据式(18)对第j个量子比特的旋转角为[6]
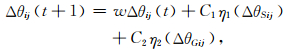
|
(19) |
其中ΔθSij、ΔθGij分别为自身历史最优解和群体历史最优解对应的量子比特相角与所考虑量子比特相角差在区间[-π,π]内的主值.用量子旋转门U对相应量子比特进行操作,依突变率随机对相应量子比特用Pauli-X门进行操作
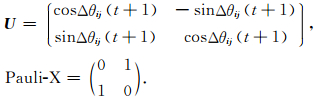
|
(20) |
(3)解码.得到一个新的粒子群体后,用式(9)对量子比特进行解码,得到新的模型参数.
(4)计算目标函数.
(5)评价.依据平均相对残差最小的原则筛选当代最优解和最优目标函数值并与历史最优解相比较,更新.当群体平均相对残差大于收敛参考值且迭代未达最大进化代数时,返回第(2)步循环.
以上三种量子反演方法发展比较迅速,已经在一些研究领域得到了应用.但各种方法针对具体问题的适应性还有待考量,这依赖于算法普适性研究和算法应用研究两方面的努力.尝试将尚未成熟的量子反演方法应用于新领域,无论对算法改进还是对具体领域研究都将起到推动作用.
4 反演实例利用上述三种反演方法,本文分别对理论模型和实际观测结果进行了反演实验.
4.1 理论模型反演实验反演实验采用的三层带电圆盘雷云荷电理论模型的不变参数为雷云半径a=3000m,云顶高hP=10000m,云底高hN=1500m,下部正电荷区底边高hL=3300 m,厚400 m.反演参数为各层电荷密度ρP、ρN、ρL(绝对值范围在0.01~3nC·m-3)和偶极层高度hB(范围在4000~7000m).反演结果见表 1.
|
|
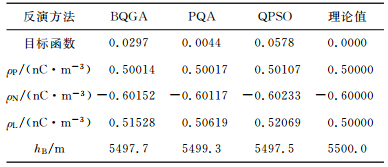
表 1 三种方法理论模型反演结果 Table 1 Theoretic model inversion result |
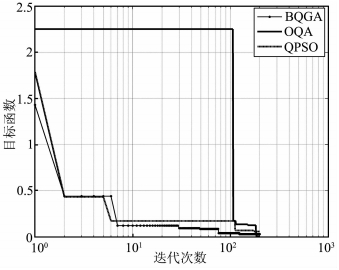
从表 1中可以看到PQA反演的目标函数最接近理论值,约为0.0044.图 2为三种方法理论模型反演的收敛曲线,图 3为三种方法理论模型的反演结果.
|
图 2 三种方法理论模型反演收敛曲线 Fig. 2 Convergent curves of theoretic model inversion results with three methods |
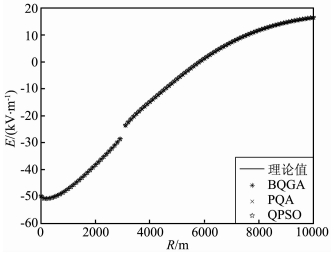
|
图 3 三种方法理论模型反演结果 Fig. 3 Theoretic model inversion results |
从图 2中可以看到针对带电圆盘雷云荷电模型,在理论模型反演过程中PQA的反演精度最高,而BQGA全局收敛速度最快.从图 3中可以看到三种方法的反演结果都与理论值符合得比较好.
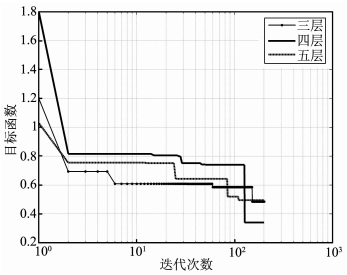
4.2 观测结果反演实验由于BQGA的全局收敛速度最快,选择用其进行雷云地面电场观测数据的反演实验.观测数据由倒置式大气电场仪采集,采集地点为泰山,采样频率为1Hz,由时间序列转换为距离序列.反演参数设置与理论模型反演实验相同,为各层电荷密度(绝对值范围在0.01~3nC·m-3)和偶极层高度(范围在4000~7000 m).考虑到对所反演雷云荷电结构没有先验知识,本文分别用三层、四层和五层模型进行了反演实验,取其中最优结果.图 4为所用的雷云地面电场观测数据,图 5为各模型的反演收敛曲线.
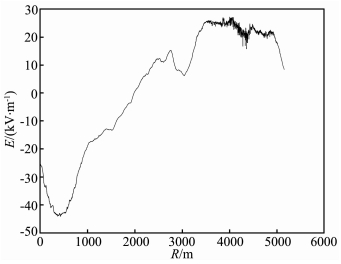
|
图 4 地面电场观测数据(泰山,2007) Fig. 4 E-field above earth surface (Mountain Tai, 2007) |
|
图 5 三层、四层、五层模型反演收敛曲线 Fig. 5 Convergent curves of three-layer, four-layer and five-layer models inversion results |
从图 5中可以看出对四层模型反演的收敛精度最高,目标函数约为0.35.这是由实际雷云多层荷电结构与算法精度共同决定的结果.
应当指出,由于观测数据的非无限性和误差性,任何地球物理学反演问题的解都具有非惟一性,雷云荷电模型反演问题同样如此,但这并不妨碍对解的评价.对于非线性反演问题,通常采用的策略为发展新的反演方法和模型构制,并对解空间进行更严格的限制.综上所述,依赖观测手段对实际雷云结构进行正确判断并合理选择反演算法是精确有效地进行具体雷云荷电反演的两个前提.
5 结论本文分别利用基于Bloch坐标的量子遗传算法、路径积分蒙特卡罗量子退火算法和量子粒子群算法对Amoruso和Lattarulo提出的带电圆盘模型进行了反演.通过对理论模型和实际地面电场观测数据的反演实验,证明了雷云荷电模型量子反演的可行性与精确性,总结了反演规律,对雷电物理学的发展和雷电防护新理论与新技术的研究具有指导意义.
| [1] | Golde R H. Physics of Lightning. London: Academy Press Inc, 1977 . |
| [2] | 陈渭民. 雷电学原理. 北京: 气象出版社, 2006 . Chen W M. Lightning Theory (in Chinese). Beijing: China Meteorological Press, 2006 . |
| [3] | Rakov Vl A, Uman M A. Lightning:Physics and Effects. Cambridge: Cambridge University Press, 2003 . |
| [4] | Edward R Mansell, Donald R, Conrad L Ziegler. Charge structure and lightning sensitivity in a simulated multicell thunderstorm. Journal of Geophysical Research , 2005, 110: D12O1. DOI:10.1029/2004JD005278 |
| [5] | 王家映. 地球物理反演方法概述. 工程地球物理学报 , 2007, 4(1): 1–3. Wang J Y. Introduction to Geophysical Inverse Problems. Chinese Journal of Engineering Geophysics (in Chinese) , 2007, 4(1): 1-3. DOI:10.1088/1742-2132/4/1/001 |
| [6] | 李士勇, 李盼池. 量子计算与量子优化算法. 哈尔滨: 哈尔滨工业大学出版社, 2009 . Li S Y, Li P C. Quantum Computation and Quantum Optimization Algorithms (in Chinese). Harbin: Harbin Institute of Technology Press, 2009 . |
| [7] | Francesco Lattarulo.李庆民, 李清泉译.电力系统中的电磁兼容.北京:机械工业出版社, 2008 Francesco Lattarulo. Li Q M, Li Q Q trans. Electromagnetic Compatibility in Power System (in Chinese). Beijing:China Machine Press, 2008 |
| [8] | Amoruso V, Lattarulo F. Thundercloud pre-stroke electrostatic modeling. Electrostatics , 2002, 56: 255-260. DOI:10.1016/S0304-3886(02)00070-0 |
| [9] | Van Bladel. Singular Electromagnetic Fields and Sources. New York: IEEE Press, 1991 . |
| [10] | 王竹溪, 郭敦仁. 特殊函数概论. 北京: 北京大学出版社, 2000 . Wang Z X, Guo D R. An Introduction to Special Functions (in Chinese). Beijing: Peking University Press, 2000 . |
| [11] | Lajos Diósi. A Short Course in Quantum Information Theory. New York: Springer, 2007 . |
| [12] | 李承祖. 量子通信和量子计算. 长沙: 国防科学技术大学出版社, 2000 . Li C Z. Quantum Communication and Quantum Computation (in Chinese). Changsha: National University of Defense Technology Press, 2000 . |
| [13] | Han K H, Kim J H. Genetic algorithm and its application to combinational optimization problem. Proceedings of the International Congress on Evolutionary Computation. IEEE Press, 2000 |
| [14] | Han K H, Kim J H. Quantum-Inspired Evolutionary Algorithm for a Class of Combinational Optimization. IEEE Trans on Evolutionary Computation, 2002 |
| [15] | Khorsand A R, Akbarzadeh M R. Quantum Gate Optimization in a Meta-level Genetic Quantum Algorithm. 2005 IEEE International Conference on Systems, Man and Cybernetics, 2005 |
| [16] | 罗红明, 王家映, 朱培民, 等. 量子遗传算法在大地电磁反演中的应用. 地球物理学报 , 2009, 52(1): 260–267. Luo H M, Wang J Y, Zhu P M, et al. Quantum genetic algorithm and its application in magnetotelluric data inversion. Chinese Journal of Geophysics (in Chinese) , 2009, 52(1): 260-267. DOI:10.1002/cjg2.v52.1 |
| [17] | 杜卫林, 李斌, 田宇. 量子退火算法研究进展. 计算机研究与发展 , 2008, 45(9): 1501–1508. Du W L, Li B, Tian Y. Quantum annealing algorithms:state of art. Journal of Computer Research and Development (in Chinese) , 2008, 45(9): 1501-1508. |
| [18] | Tadashi K, Hidetoshi N. Study of optimization problem by quantum annealing. Tokyo: Tokyo Institute of Technology, 1998 . |
| [19] | Lee Y, Berne B J. Global optimization:quantum thermal annealing with path integral Monte Carlo. Journal of Physical Chemistry A , 2000, 104: 86-95. |
| [20] | Liu P, Berne B J. Quantum path minimization:an efficient method for global optimization. Chemical Physics , 2003, 118: 2999-3005. |
| [21] | 魏超, 朱培民, 王家映. 量子退火反演的原理和实现. 地球物理学报 , 2006, 49(2): 578–583. Wei C, Zhu P M, Wang J Y. Quantum annealing inversion and its implementation. Chinese J. Geophys. (in Chinese) , 2006, 49(2): 578-583. |
| [22] | 魏超, 李小凡, 张美根. 量子退火最优化与地球物理反演方法. 地球物理学进展 , 2007, 22(3): 785–789. Wei C, Li X F, Zhang M G. Quantum annealing optimization and geophysical inverse method. Progress in Geophysics (in Chinese) , 2007, 22(3): 785-789. |
| [23] | 李盼池. 基于量子位Bloch坐标的量子遗传算法及其应用. 控制理论与应用 , 2008, 25(6): 985–989. Li P C. Quantum genetic algorithm based on Bloch coordinates of qubits and its application. Control Theory and Applications (in Chinese) , 2008, 25(6): 985-989. |
| [24] | 罗红明, 王家映, 师学明, 等. 量子路径积分算法及其在大地电磁反演中的应用. 地球物理学报 , 2007, 50(4): 1268–1276. Luo H M, Wang J Y, Shi X M, et al. Quantum path integral algorithm and its application in magnetotelluric inversion. Chinese J. Geophys. (in Chinese) , 2007, 50(4): 1268-1276. |
| [25] | 白铭复, 陈健华, 田成林. 高等量子力学. 长沙: 国防科学技术大学出版社, 1994 . Bai M F, Chen J H, Tian C L. Advanced Quantum Mechanics (in Chinese). Changsha: National University of Defense Technology Press, 1994 . |
| [26] | Mikki S M, Kishk A A. Quantum Particle Swarm Optimization for Electromagnetic. IEEE Trans on Antennas and Propagation, 2006 |
 2010, Vol. 53
2010, Vol. 53


 , 万浩江
, 万浩江