电测井和油气层关系的核心是电导率和饱和度的关系.1942年发表的阿尔奇公式[1]是关于电阻率和孔隙度、饱和度关系的两个实验公式,即地层因素公式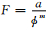
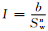
本文利用电场理论研究砂岩电导率和油气饱和度的关系.导体和电介质中的电场向来是分开研究的[2, 3],导体中形成电流场,用J=σE和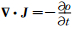
砂岩是由几种电介质(骨架、油、气)和导体(孔隙水或双水[5, 6])组成的混合物,物质之间有一定的弥散.在砂岩所在区域V中垂直于平均电流方向上任取一面积为Δs的截面,截面上导体的相对面积为ϕSw.导体的电导率记为σc.记J为截面上的平均电流密度,流出截面的电流就是ΔsJ.记〈J〉为截面上导体的平均电流密度,流出截面的电流又可写成ΔsϕSw〈J〉.流出截面的电流应该相等,则
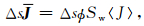
|
(1) |
即
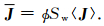
|
(2) |
在V上对欧姆定律求平均则有
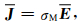
|
(3) |
式中,E为平均电场强度,σM是根据积分中值定理得出的岩石的整体电导率.在导体上对欧姆定律求平均得
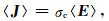
|
(4) |
式中,〈J〉是导体上的平均电流密度,〈E〉是导体上的平均电场强度.式(3)、(4)代入式(2)得
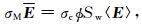
|
(5) |
由此定义电导率:

|
(6) |
下面研究电流通过砂岩时导体和电介质颗粒分界面上的电场性质.根据麦克斯韦方程
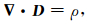
|
(7) |
电流通过砂岩时导体和电介质颗粒分界面上导体一侧会出现自由面电荷,分界面导体一侧的电流密度法向分量为零,从而电场强度的法向分量为零,电介质一侧的电流密度法向分量也应为零,但因电介质的电导率为零,电场强度的法向分量就不都为零.设电场E的方向为n,电介质和导体分界面法线方向n0由电介质外部指向内部,自由面电荷密度ρs等于电介质一侧电位移矢量的法向分量,即
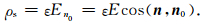
|
(8) |
界面上的面电荷有正负两种,当cos(n,n0)为正时可视为正电荷,当cos(n,n0)为负时可视为负电荷,并由负到正形成若干电偶极子,电偶极子方向与n相反.在分界面的第i个面元Δsi上,对应的电偶极子电荷为εE|cos(n,n0)|Δsi,|cos(n,n0)|Δsi是Δsi在垂直于n的平面上的投影,正、负面电荷相距为li,对应部分颗粒的体积为Δτi,则Δsi处的面电荷形成界面偶极强度PΔs为
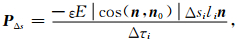
|
(9) |
因|cos(n,n0)|Δsili=Δτi、En=E,则
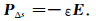
|
(10) |
对上式在单个颗粒界面s上求平均得到平均界面偶极强度:
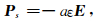
|
(11) |
其中a是形成电偶极子的部分表面占颗粒表面的比率,在导体颗粒上a=0.
电场中的电介质颗粒内极化后产生极化强度Pv:

|
(12) |
其中χe是电极化率.仿电位移矢量的定义,令
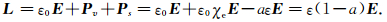
|
(13) |
εr是相对介电常数,L是联合强度.记λ=ε(1-a),则
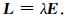
|
(14) |
L一定是无源的,所以
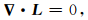
|
(15) |
式中▽为哈密顿算子.
在V上对式(14)求平均则有

|
(16) |
式中,λM是根据积分中值定理得出的砂岩整体的λ值.
将式(14)在岩石所在的V中同一物质成分v上求平均,根据积分中值定理λ已经取某个值,则有
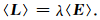
|
(17) |
于是,〈L〉和〈E〉都与λ一样,在同一物质成分上各点的值相同,在不同物质成分上各点的值不同.
3 砂岩电场方程设点Q(x′,y′,z′)只在点P(x,y,z)所在的那种物质成分所占的区域v上变化,则〈L〉的表达式是
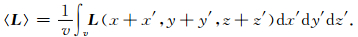
|
(18) |
由于不同的物质颗粒是相互掺杂在一起的,上式右端求平均实际上是分两步进行的,第一步先对同一颗粒求平均,第二步再对同一成分的所有颗粒求平均.上式对点P(x,y,z)求散度,则
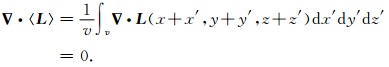
|
(19) |
将E=E+δE在同一物质成分v上求平均得
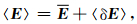
|
(20) |
再将岩石整体的λM和各成分的λ的关系记为

|
(21) |
式中Δλ仅为λ与λM的差值变量.将式(20)、(21)代入式(19)得
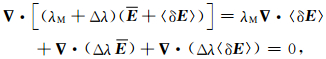
|
即
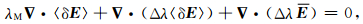
|
(22) |
(22)式两端求梯度,注意到▽ × 〈δE〉=0,则有
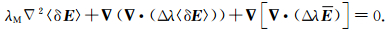
|
(23) |
设E沿n方向,并在式(23)中取n方向的分量,注意到从式(5)可以推出导体上的〈δE〉沿n方向,从而电介质上的〈δE〉也沿n方向,则有
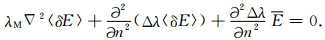
|
(24) |
设岩石各点的λ变化最大的方向为m,可将式(24)写成如下形式:
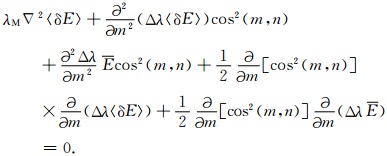
|
(25) |
由于在任何点上,沿m方向cos(m,n)不变,所以(25)式变为
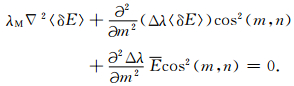
|
(26) |
因为任何点的m方向就是该点Δλ及〈δE〉变化最大的方向,也就是该点的梯度方向,所以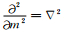
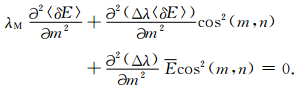
|
(27) |
对同一种成分来说,(27)式中只有cos2(m,n)是变化的,在同一种成分上对(27)式求平均,cos2(m,n)的平均值记为〈cos2(m,n)〉,则
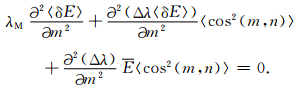
|
(28) |
这是砂岩电场方程.
4 砂岩电导率公式由式(28)可得
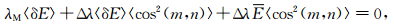
|
(29) |
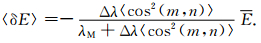
|
(30) |
(30)式两端加E得

|
(31) |
对(31)式在V上求体积平均得
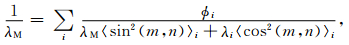
|
(32) |
式中〈sin2(m,n)〉i=1-〈cos2(m,n)〉i,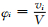
式(31)在导体成分上的形式代入式(6)得岩石电导率公式:
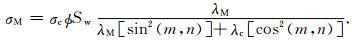
|
(33) |
式中λc是导体的介电常数.
4.1 单个小电介质球放在水的中间
在此系统中,小球的λg=0,经计算〈cos2(m,n)〉=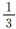
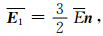
|
(34) |
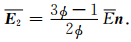
|
(35) |
经分离变量法求解,球内的平均电场、球外的平均电场、系统的平均电场分别为
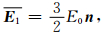
|
(36) |
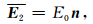
|
(37) |
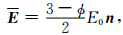
|
(38) |
式中,E0n是小球放入以前的电场强度.当ϕ接近1时,两种方法所得结果一致,证明把颗粒面电荷等效为电偶极子的方法是有效的.
4.2 电介质球分散在水中
在此系统中,小球的λg=0,经计算〈cos2(m,n)〉=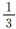

|
(39) |
在麦克斯韦公式[1]
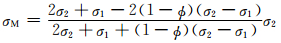
|
(40) |
中,介质球外的电导率为σ2,介质球的电导率为σ1,所有小球的体积和整个系统的体积之比为1-ϕ,小球的半径比小球之间的距离小得多,1-ϕ必然是个很小的数,令σ1=0,可得
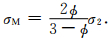
|
(41) |
经计算可知,在ϕ>0.8时,式(39)和(41)是一致的,在适应的范围内两个公式一样好.
4.3 饱和水玻璃球堆积
经计算,在颗粒上〈cos2(m,n)〉=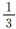
|
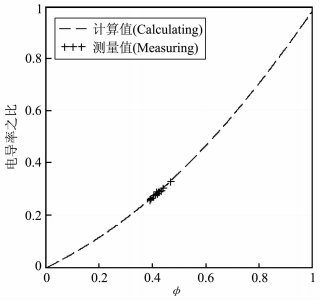
图 1 玻璃球堆积的电导率和水的电导率之比 Fig. 1 The ratio of crystal balls conductivity and water conductivity |
|
|
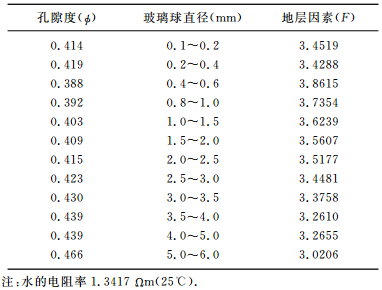
表 1 玻璃球堆积的地层因素测量结果 Table 1 Formation factor (F) about crystal balls obtained by laboratory |
〈cos2(m,n)〉取为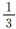
|
|
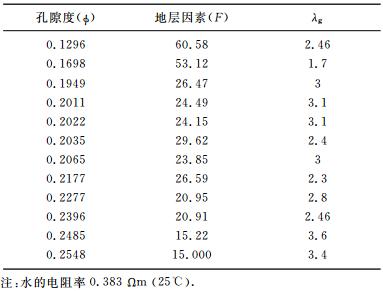
表 2 饱和水砂岩测量结果 Table 2 Sandstone formation factor (F) obtained by laboratory and λg by formula (33) |

|
图 2 砂岩的地层因素 Fig. 2 The formation factor of sandstone |
〈cos2(m,n)〉取为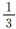
|
|
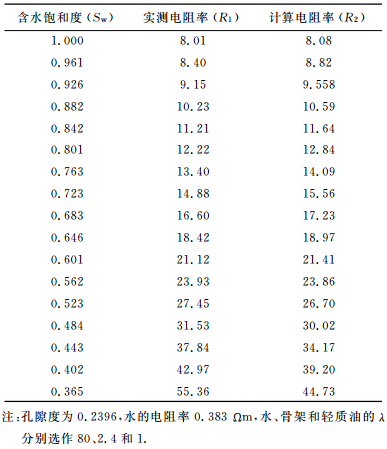
表 3 砂岩饱和度和电阻率 Table 3 Sandstone resistivity obtained by:R1 measuring in aboratory, R1 calculating with (33) |
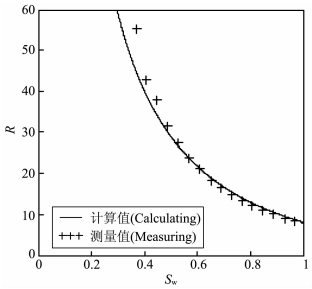
|
图 3 电阻率随含水饱和度的变化 Fig. 3 The resistivity and water saturation of sandstone |
从电场理论来看,砂岩电导率为地层水电导率、含量、相对电场强度的积.从本文提出的电介质颗粒面电荷形成反电场方向极化强度的认识来看,相对电场强度是由介电常数、同种颗粒间接触面、结构决定的.从实际应用角度来看,核心是决定a和〈cos2(m,n)〉,针对这个问题,作者提出了数字岩心技术,已规模化应用到测井评价油气的生产中.
致谢感谢王伟男提供砂岩实验数据,感谢孙宝佃提供玻璃球堆积实验数据.
| [1] | Archie G E. The electrical resistivity log as an aid in determining some reservoir characteristics. Trans. A.I.M.E. , 1942, 146: 54-62. |
| [2] | 杰·克·麦克斯韦著.电磁通论.戈革译.武汉:武汉出版社, 1992. 488~492 Maxwell J C. A treatise on electricity and magnetism (in Chinese). Translated by Ge G. Wuhan:Wuhan Press, 1992. 488~492 |
| [3] | 毕得显. 电磁场理论. 北京: 电子工业出版社, 1985 . Bi D X. Electromagnetism field theories (in Chinese). Beijing: Electronics Industrial Press, 1985 . |
| [4] | 李剑浩. 混合物整体电导率的研究. 地球物理学报 , 2005, 48(6): 1406–1411. Li J H. Study on the whole conductivity of mixture. Chinese J. Geophys. (in Chinese) , 2005, 48(6): 1406-1411. |
| [5] | Clavier C, Coates G, Dumanoir J. The theoretical and experimental bases for the "dual water" model for the interpretation of shaly sands, SPE6859, 1977 |
| [6] | 李剑浩. 用混合物电导率公式改进双水模型的公式. 测井技术 , 2007, 31(1): 1–3. Li J H. An improvement in conductivity formula of dual water model with conductivity formula of mixture. WLT (in Chinese) , 2007, 31(1): 1-3. |
 2010, Vol. 53
2010, Vol. 53