实现地震资料反演是确定地层岩性、识别储层流体、提高地震解释精度的重要方法和途径^[1~8]，因此地层密度和岩石物理参数反演一直是地震反演的热点问题之一^[9~18].Zoeppritz方程是AVO（Amplitude Versus Offset）或AVA（Amplitude Versus incident Angle）反演技术的基础^[11~18].但由于方程解的复杂性，致使目前的AVO（或AVA）反演几乎都是基于Zoeppritz方程近似实现的，适应于弱反射介质界面、小偏移距反射问题.但在实际勘探中已遇到了大量的非弱反射界面（包括小角度范围）及大角度甚至是广角反射问题^[19~31]（井间地震、深水探区等），这些问题难以满足Zoeppritz方程近似式成立的条件^{[19~21, 24~30]}，这种近似会给计算带来较大的误差，不能满足勘探开发对计算的需求，需要寻找更准确的反演计算方法，拓展叠前反演方法的使用范围，提高计算精度.因此研究基于Zoeppritz方程的反演偏导矩阵高精度计算方法十分必要.文献[31]给出了地震波反射系数对地层纵横波速度导数的准确计算方法，实现了反演纵横波速度偏导矩阵的准确计算^[31]，但没有给出地震波反射系数对地层密度偏导数的计算方法.因在地震波速度中隐含着介质的密度，使计算反射系数对地层介质密度比偏导数复杂化，更增加了利用反射系数反演介质密度的难度.但由于地层密度是反映地层岩性十分重要的参数，因此在不简化Zoeppritz方程条件下开展包括适合于大角度反射问题的地层密度反演将具有实际意义，其关键是偏导矩阵精确计算的实现.在Zoeppritz方程中由于反射系数与介质密度是一个十分复杂的非线性关系，因此在许多反演计算中往往将反射界面两侧介质的密度比作为一个变量研究.本文基于这一思路以精确求解Zoeppritz方程为手段，实现了用于反演介质密度比偏导矩阵的精确计算，克服了Zoeppritz方程近似式所遇到的困难，为进一步利用反射系数反演地层介质密度及解决大角度入射波反演问题提供了重要的理论依据.

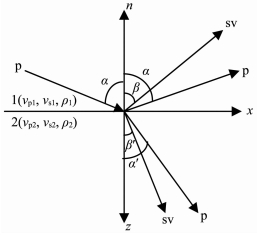
如图 1，其中p，sv分别表示p，sv地震波.α为p波入射角，β为转换波sv的反射角；α′，β′分别为透射p，sv波的折射角；v_p1、v_s1、ρ₁、v_p2、v_s2、ρ₂分别为波在介质1、2中的p、sv波的速度和介质的密度.

图 1

Fig. 1

图 1 P波在界面的反射和透射 Fig. 1 Reflection and refraction of a P-wave at an interface between two elastic media

在边界地震波满足位移和应力连续的Zoeppritz方程^{[7, 8]}

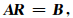
(1)

其中

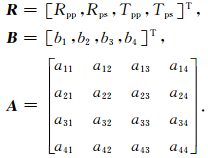
(2)

R_pp、R_ps、T_pp、T_ps分别为入射p波、反射p，sv波和折射p、sv波的反射和折射系数.在公式（2）中上标T表示矩阵的转置，

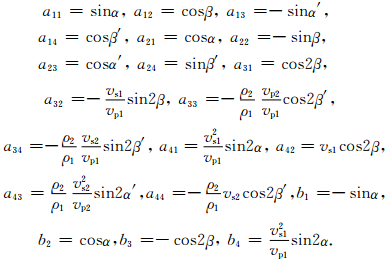
设在反射界面两侧介质的密度比为ρ₂₁=ρ₂/ρ₁，将Zoeppritz方程两边对ρ₂₁求导得

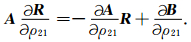
(3)

在（3）式中矩阵A与入射角有关.利用Zoeppritz方程（1）可计算反射系数R，只要计算出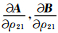，由方程（3）则可计算反射系数对介质密度比的偏导数.

在同一种均匀弹性介质中纵横波速度分别为

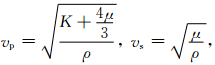
(4)

其中K，μ分别为弹性介质的体变弹性模量和切变弹性模量，ρ为介质的密度.若两种介质的密度比为ρ₂₁=ρ₂/ρ₁，则有

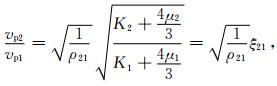
(5)

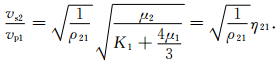
(6)

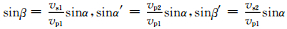
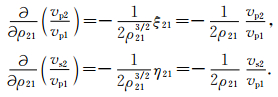
因所以有

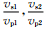
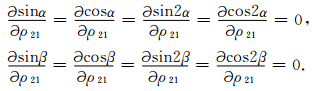
由（4）式知与ρ21无关（不包含ρ₂₁），所以

而

同理.所以有

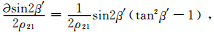
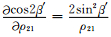
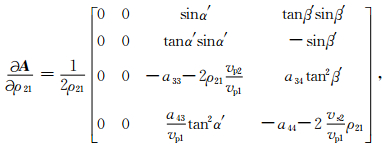
(7)

其中

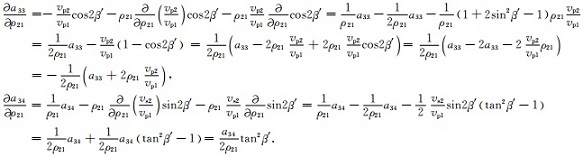
将矩阵形式的Zoeppritz方程（1）的第4行的矩阵元素a₄₃、a₄₄除以v_p1并对ρ₂₁求导得

3.2 矩阵的计算

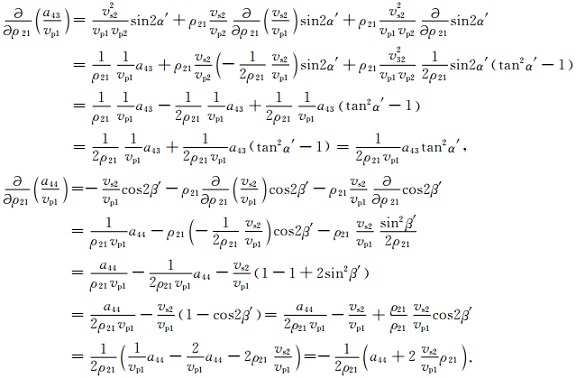
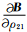
矩阵B各矩阵元为

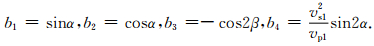
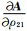
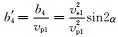
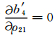
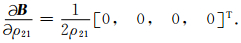
因在计算时矩阵形式的Zoeppritz方程（1）第4行两边需要同除v_p1（在对ρ₂₁求导时），所以，与ρ21无关，则有.矩阵B对ρ₂₁的导数为

(8)

为对反射系数对介质密度比偏导数给出一个直观的认识和了解，选择文献[8]（陆基孟1993，P166）中算例参数，分别计算了反射系数对介质密度比的偏导数.当v_p2＞v_p1时参数取值为^[8]：v_p1=3500 m/s，v_p2=v_p1/0.62=5645 m/s；v_s1=v_p1/1.7=2058m/s，v_s2=v_p2/1.7=3320m/s；ρ₂/ρ₁=1.266.第一临界角α_c=38.316°，在所选参数条件下不存在第二临界角.图中字符表示：，.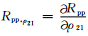

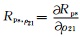
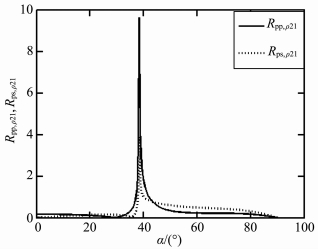
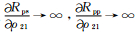
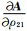
图 2为入射p-波，反射p-波反射系数对ρ₂₁的导数曲线（导数的大小，即导数的模）.曲线在第一临界角（算例α_c=38.316°）处存在锐峰（实际上是间断点，在α_c点，这是因为矩阵的矩阵元含有tanα′项所致），由于导数的奇异性易造成较大的计算误差，这在做介质密度反演时应特别注意在临界角附近偏导数的求取.为便于了解在其他入射角R_pp、R_ps对ρ₂₁导数的变化，分别做出了图 3a、图 3b.图 3a中R_ps对ρ₂₁的导数存在零点，约在α=43°的地方曲线R_pp，ρ21、R_ps，ρ21存在交点. 图 4a、图 4b为反射系数R_pp、R_ps对ρ₂₁导数的实部和虚部曲线，在大多数入射角范围内R_ps对ρ₂₁导数的实部是负的.曲线R_pp，ρ21、R_ps，ρ21在第一临界角处均存在奇异点.从这两张图可以发现在入射角小于临界角范围内反射系数R_pp、R_ps对ρ₂₁导数的虚部始终为零，反射系数为实数，与实际相符合，这一点验证了程序及所导公式的正确性.

图 2

Fig. 2

图 2 反射系数Rpp、Rps对介质密度比ρ21的导数() Fig. 2 artial derivatives of reflection coefficients Rpp and Rps with respect to ρ21

图 3

Fig. 3

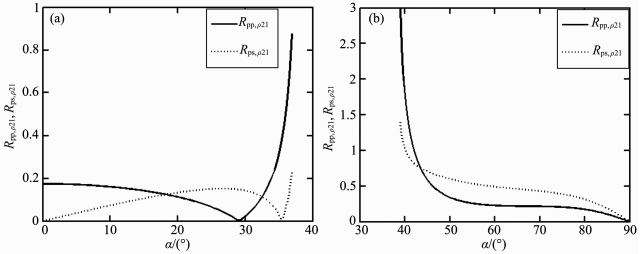
图 3 反射系数Rpp、Rps对介质密度比ρ21的导数 Fig. 3 Partial derivatives of reflection coefficients Rpp and Rps with respect to ρ21

图 4

Fig. 4

图 4 反射系数Rpp、Rps对介质密度比ρ21导数的实部和虚部 Fig. 4 Real and imaginary parts of partial derivatives of reflection coefficients Rpp and Rps with respect to ρ21

图 5是透射系数T_pp、T_ps对介质密度比ρ₂₁的导数，与图 2类似在临界角附近曲线变化比较剧烈.

图 5

Fig. 5

图 5 透射系数Tpp、Tps对介质密度比ρ21的导数 Fig. 5 Partial derivatives of refraction coefficients Tpp and Tps with respect to ρ21

上面的计算表明（图 2~图 5）反射系数对密度比的导数在第一临界角均存在异常，第一临界角是R_pp、R_ps对介质密度比ρ₂₁导数的间断点，是R_pp、R_ps对介质密度比ρ₂₁导数曲线的折点，形成了明显的临界角标志，这可被用于反射波临界角的识别，也可被用于研究反射界面两侧介质密度的变化.

由Zoeppritz方程通过对方程求导建立了反演介质密度比的偏导方程，导出了Zoeppritz方程各矩阵元对介质密度比的偏导数.通过求解偏导方程实现了反演介质密度比偏导矩阵的精确计算，克服了目前AVO（或AVA）反演使用Zoeppritz方程近似所遇到的困难.该方法不仅适应于弱反射介质界面和小偏移距反射问题，而且还适用于非弱反射界面及大角度反射问题，扩大了使用范围.利用算例还分析了反射系数对介质密度比偏导数的特点，结果显示：反射系数对介质密度比的导数在第一临界角曲线存在间断点，形成了明显的临界角标志，这一特点在对大角度反演问题值得注意；当入射角大于第一临界角后反演偏导矩阵变为复数，其实部和虚部包含了大量的地层岩石物性参数信息，各自的地球物理意义、在反演中如何应用有待于更为深入的研究.反演介质密度偏导矩阵精确计算的实现，为优化选择反演角度，消除反射系数及反射系数偏导数出现奇异和接近零的反演角度，建立多角度反演方法，为进一步实现地层介质密度反演，提高计算速度和反演精度将具有重要的实际意义.