2. 中国石油勘探开发研究院石油物探技术研究所, 北京 100083
2. Department of Geophysical Exploration Technology, Research Institute of Petroleum Exploration & Development, Beijing 100083, China
地震数据通常非常巨大,而且由于实际采集状况的复杂性,比如仪器或者现场环境等,采集到的数据常常不完整或者有坏道需要剔除[1~3].但后续处理(如偏移等)又对数据的完整性有很高的要求.因此,地震数据的压缩和重建有着非常重要的意义.
根据传统的Shannon/Nyquist采样理论,只有当采样频率不低于目标信号最大频率的二倍时,才能实现不完整数据的较理想重建,否则,将会出现假频现象,严重影响后续处理.然而在实际工作中,一方面为了获得高质量的恢复效果,希望所拥有的数据越多越好,另一方面由于采集的原因,得到的数据很不完整,或者希望能尽可能少地布置炮点和接收点以节省成本.这两者似乎是不可调和的矛盾.换句话说,如果我们能只利用很少的数据就可以重建将会有重要意义.但这种利用极少数据(如20%)来恢复全部数据的问题,从信息重建的地球物理反演角度来说,显然是欠定的,在数学上很难求解.信息技术领域新发展起来的压缩感知理论[4, 5]为解决此类问题提供了新的契机.根据压缩感知理论,即使是基于欠采样数据,也有可能恢复出满足一定精度要求的完整数据.它的策略是利用随机欠采样方法将传统规则欠采样所带来的互相干假频转化成较低幅度的不相干噪声,从而仍可以很容易地检测到真正的频谱,最后通过一种最小化策略进行求解.其实,这种求解欠定问题的思想在地球物理领域并不鲜见[6~9],而经过系统地整理和证明完善并形成压缩感知理论(Compressed Sensing/Compressive Sampling)后,这种技术在诸多领域都获得了快速的发展,如图像处理、核磁共振成像[10]等.
对于地震数据的恢复重建,一种广泛使用的方法是基于某种变换,如Radon变换[11~13],Curvelet变换[9, 14],傅里叶变换[2, 3, 6~8, 15~17]等.这里我们选用使用最广泛的傅里叶变换.另一方面,根据压缩感知理论,要获得理想的重建效果,需要采用随机欠采样方法,以使传统规则欠采样所引入的和真实频率相混淆的假频转化成容易去除的不相干噪声[7].而在诸多文献中,大部分基于傅里叶变换和压缩感知的恢复算法采用的是单纯随机采样,这是一种最直观简单的方法.但是,简单的纯随机采样有其固有的缺陷,即不能控制采样间距,可能造成某些重要信息的缺失,而且容易出现采样点聚集现象,造成某些区域采样过密.
为了改善基于傅里叶变换和压缩感知的重建方法中单纯随机欠采样方法的不足,我们引入具有蓝色噪声频谱特征的泊松碟欠采样方法[18~20].与单纯随机采样方法相比,这种方法在保持随机性的同时,使采样点的分布更加均匀,可以弥补单纯随机采样的不足.文中首先简要介绍基于压缩感知理论和傅里叶变换的地震数据压缩重建方法,然后定义一个评价欠采样方法优劣的度量函数.最后引入泊松蝶欠采样,并与单纯随机采样方法做了对比.
2 重建方法地震数据的压缩重建问题可以描述为由一组不完整数据通过线性算子的作用恢复出完整的数据,如以下模型所示
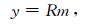
|
(1) |
其中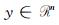
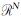
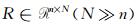
在方程(1)中,N>>n,很显然这是一个欠定的病态问题,其解并不惟一,也就是说,根据传统的理论,通过这个方程很难理想地重建出m.而压缩感知理论为恢复m提供了可能,其要求是满足以下三个条件:(1)m是稀疏的或者可压缩的,至少在某个变换域里满足此条件;(2)采用随机欠采样方法,即R矩阵是由随机的(0,1)元素组成的,使相干噪声转化为不相干的噪声而将其滤除;(3)选用有效的求解策略,在保证数据一致性的同时寻找稀疏解,以达到求解该欠定问题的目的.
如果m在某一个变换域S的系数x是稀疏的,即x=Sm,则方程(1)可写成以下形式:
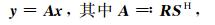
|
(2) |
其中,上标H表示共轭转置.这里用算子矩阵S来表示某种稀疏变换,SHS=I,即变换矩阵S是酉矩阵.
当y是不完整的欠采样数据时,即矩阵A是奇异的,这个欠定问题的解并不唯一.但如果x是稀疏的,这个问题仍然可以求解.也就是说,可以通过不断促进x的稀疏性来进行反演求解这个欠定方程.于是,重建信号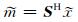

|
(3) |
其中x=Sm是m在变换域S的系数,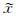
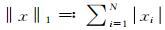
方程(3)中的第一项是稀疏促进项,第二项是为了保持数据的一致性,即通过以上的1-范数最小化,不断促进x的稀疏性,而一致性约束条件y=RSHx则保证了该问题的解向真值的方向不断收敛.也就是说,在欠定方程(2)的所有可能解中,方程(3)通过不断的优化过程,以寻求其中能满足约束条件的最稀疏解[21, 22].当通过方程(3)估计出系数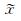
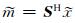
对于采样方法R,根据压缩感知理论[4, 5],应该使采样具有一定的随机性以使其互不相干,如本文将要进行对比讨论的单纯随机采样和泊松碟采样方法.对于稀疏变换基S,本文采用傅里叶变换,即定义S=:F.接下来我们将用Fp=:RFH来表示不完全采样的傅里叶算子.而自压缩感知理论提出以来,研究者们已经发展了诸多方法来求解约束问题(3),这里选用谱投影梯度法来求解此1-范数最小化问题(Spectral projected-gradient for L1-norm problems,简称SPGL1)[23].至此,前述压缩感知所要求的三个条件,都可以得到满足,继而可以进行欠采样地震数据的恢复重建.
3 傅里叶域互相干噪声评价函数压缩感知的关键技术之一是随机欠采样方法,因为它可以把混淆真实频率的相干噪声转化成容易滤除的不相干噪声.因此,相干噪声的程度,很自然地就成为衡量一种欠采样方法效果的重要标准[20].定义稀疏采样矩阵的格拉姆(Gram)矩阵如下:
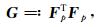
|
(4) |
其中上标T表示转置.通过Gram矩阵的元素gij,就可以衡量两个不同位置点i和j的相互影响程度,即互相干程度.事实上,对于任何一个点i,如果将其他各点j(j≠i)的Gram值画在一张图上,那么这张图就显示出其他所有点对点i的互相干影响程度.而这个影响程度要尽可能地小,否则这些相干噪声就会对数据的重建造成较大影响.更进一步地,定义点扩散函数(Point spread function,缩写PSF)[10]
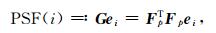
|
(5) |
其中ei表示一个单位向量,即只在第i点非零.PSF函数表示其他各点对第i点的影响程度.对于满足Nyquist采样要求的充分采样来说,几乎不存在互相干噪声,所以PSF(i)只在第i点非零.但是欠采样引入了相干噪声,PSF(i)函数在其他各点的值并不是全部为零,而在这些点处值的大小则反映了互相干程度的强弱.由此便可以用PSF函数图来衡量一种采样方法对于压缩重建的优劣.
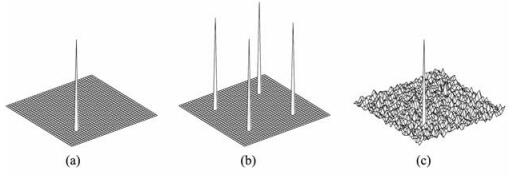
4 采样方法 4.1 规则采样与随机采样对于规则采样来说,相邻采样点之间的间隔是相等的,在满足Nyquist采样要求的情况下,并不会导致频率混淆,否则,将带来相干假频.下面通过一个模型实例来说明此问题,图 1a是某模型的真实频谱,图 1b则是采用规则欠采样的情况,采样率为1/3,从其PSF图中可以看出,假频幅值和真值相当,以致于无法检测出真实值,而这些假频会被带入重建过程,严重影响数据恢复质量.所以,如果选用规则采样,必须满足Shannon/Nyquist采样定理的要求.如前所述,根据压缩感知理论,即使采样率严重不足,不满足Shannon/Nyquist采样要求,也有可能实现数据的理想重建,其关键要求之一就是采用随机欠采样方法,将相干噪声转化为易于滤除的不相干噪声.如图 1c所示,仍然只采样1/3的数据,但是随机采样将之前的假频转化成了低幅值的噪声,即使这些随机噪声和真实频谱相互叠合在一起,真实频率也可以很容易地被检测到.更进一步地,为了减少这种人为引入的假频的影响,希望真值周围的噪声尽可能地少,以便更好地检测到真值.这种特征,即所谓的蓝色噪声频谱特征.
|
图 1 傅里叶域归一化PSF分析 (a)某模型的真实频谱; (b)规则欠采样的PSF函数图; (c)随机欠采样的PSF函数图. Fig. 1 Normalized PSF analysis in Fourier domain (a) An example in Fourier domain, the spike denotes the actual value what we want; (b) The PSF after regular undersampling; (c) The PSF after random undersampling. |
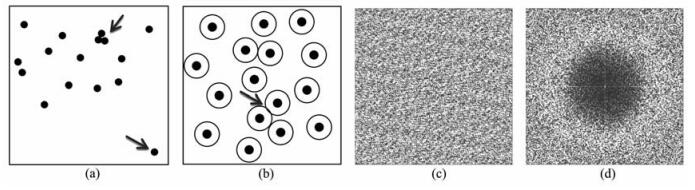
产生随机采样点的方法很多,其中最简单的一种就是单纯随机采样,即完全随机地产生一些点,除此之外没有其他约束条件.这种方法简单易用,被包括傅里叶算法在内的基于压缩感知的技术所广泛采用.但是,由于单纯随机采样是完全随机的,常常会造成采样点过于聚集,或者过于分散的情况,如图 2a所示,这就有可能对某些部分采样过多,造成信息冗余和浪费,或者对某些重要信息部分采样过少,难以达到理想的重建效果.
|
图 2 采样方法比较 (a)单纯随机采样示意图; (b)泊松碟采样示意图; (c)单纯随机采样的频谱图; (d)泊松碟采样的频谱图. Fig. 2 Sampling schemes comparison (a) Random sampling; (b) Poisson disk sampling; (c) Fourier spectrum of random sampling; (d) Fourier spectrum of Poisson Disk sampling. |
在图像处理领域广泛采用的泊松碟采样方法,则对相邻采样点间距有一定的调节能力.如图 2b所示,随机选取一些具有一定半径长度的圆圈,每个圆圈区域表示采样范围,在任一个所圈定的区域内采集一个点,同时相邻的两个采样点所在的圆圈区域不能交叉重叠,这就保证了采样点不会离得太近,使采样点分布更加均匀,同时仍然保持随机性.泊松碟采样具有著名的蓝色噪声频谱特征,如图 2d所示.蓝色噪声频谱特征是描述随机类型特征的一个统计模型,其特点是在主要频率周围分布的其他频率值都非常小,所以真值或者主频率就很容易被检测到.这种特征很类似于上述的点扩散函数,可以降低互相干噪声,更加有利于数据的恢复重建.从图 2c可以看出,与泊松碟采样相比,单纯随机采样的这种特征就很不明显.
5 数值算例采用一个合成地震叠前数据的时间切片作为例子,如图 3所示,来比较泊松碟采样和单纯随机采样在基于傅里叶变换的地震数据压缩重建中的效果.定义信噪比SNR=20log10‖f0‖2/‖f-f0‖2,其中f0表示原始模型数据,f表示重建结果.

|
图 3 时间切片模型 Fig. 3 A time-slice model |
首先对一维采样的效果进行对比,即只在该二维时间切片的某一个方向上进行一维采样,然后通过方程(3)的求解实现不完整数据的恢复重建.这里对沿检波器所分布的方向进行不规则采样,而炮点分布方向保持不变.如果采用单纯随机采样,如图 4a所示,因为对采样间距没有控制,在某些区域会出现采样间距过大的问题,很容易漏掉重要信息,另一方面,也会出现在某些区域采样过密的情况,造成采样信息冗余和浪费.而泊松碟采样使采样点分布更加均匀,可以有效地避免这种情况,如图 4b所示.从重建结果也可以看出,对于单纯随机采样,采样间隔过大的部分很难得到理想的恢复,如图 4c所示,而泊松碟采样可以很好地改善其效果,如图 4d所示.

|
图 4 一维采样道及恢复结果比较(60%道缺失) (a)单纯随机采样; (b)泊松碟采样; (c)由(a)恢复的结果, SNR=7.17 dB; (d)由(b)恢复的结果, SNR=8.34 dB. Fig. 4 Samples and reconstruction results from incomplete data with 60% missing traces through (a) ID pure random sampling; (b) ID Poisson Disk sampling; (c) reconstruction from (a), SNR=7.17 dB; (d) reconstruction from (a), SNR=8.34 dB. |
地震数据通常都含有噪声,为了对比两种采样方法在恢复不完整含噪数据方面的效果,在图 1模型中加入高斯随机噪声.图 5(a,b)分别为单纯随机欠采样和泊松碟欠采样的含噪地震道,均有60%的道数缺失.可以看出,在保持随机性的同时,泊松碟采样的地震道分布更加均匀.而从重建结果来看,即使是在含噪声的情况下,泊松碟采样的重建效果也优于简单的纯随机采样,如图 5(c,d)所示.这说明,在基于傅里叶变换的地震压缩重建中,泊松碟采样方法比纯随机采样具有更强的抗噪声能力.

|
图 5 一维含噪声数据的采样及恢复结果比较(60%道缺失) (a)单纯随机采样; (b)泊松碟采样; (c)由(a)恢复的结果, SNR=4.61 dB; (d)由(b)恢复的结果, SNR=5.42 dB. Fig. 5 Samples and reconstruction results from incomplete noisy data with 60% missing traces through (a) ID pure random sampling; (b) ID Poisson Disk sampling; (c) Reconstruction from (a), SNR=4.61 dB; (d) Reconstruction from (a), SNR=5.42 dB. |
地震数据通常是高维的,因此,发展有效的高维采样方法非常有必要.对上述的时间切片做二维采样,其恢复结果如图 6所示,从可视性和信噪比来看,泊松碟采样的效果都要优于纯随机采样.

|
图 6 二维采样恢复结果及误差图(65%缺失道) (a)单纯随机采样重建结果,SNR=9.54 dB,(b)泊松碟采样重建结果,SNR=11.52 dB,(c)和(d)分别是(a)、(b)相对于原始模型的误差图 Fig. 6 Reconstruction and residuals from 35% samples through 2D (a) Pure random sampling,SNR=9.54 dB (b) Poisson Disk sampling,SNR=11.52 dB,(c)(d) is the residual of (a)(b) respectively. |
本文主要研究了基于压缩感知和傅里叶变换的地震数据重建方法中的欠采样问题,引入了泊松碟采样,来改善传统的单纯随机采样.数值算例表明,泊松碟采样在保持采样随机性的同时,使采样点的分布更加均匀,从而有效地减少采样点过密或者过于分散的问题,更有利于数据的恢复.这是对传统单纯随机采样方法的一个有效补充.
考虑到互相干噪声直接影响着基于压缩感知技术的重建效果,下一步将研究如何更有效地利用蓝色噪声特征来减少互相干性,达到更好的恢复效果.
| [1] | Wang Y B, Luo Y, Schuster G T. Interferometric interpolation of missing seismic data. Geophysics , 2009, 74(3): S137-S145. |
| [2] | 刘喜武, 刘洪, 刘彬. 反假频非均匀地震数据重建方法研究. 地球物理学报 , 2004, 47(2): 299–305. Liu X W, Liu H, Liu B. A study on algorithm for reconstruction of de-alias uneven seismic data. Chinese J. Geophys. (in Chinese) , 2004, 47(2): 299-305. |
| [3] | 孟小红, 郭良辉, 张致付, 等. 基于非均匀快速傅里叶变换的最小二乘反演地震数据重建. 地球物理学报 , 2008, 51(1): 235–241. Meng X H, Guo L H, Zhang Z F, et al. Reconstruction of seismic data with least squares inversion based on nonuniform fast Fourier transform. Chinese J. Geophys. (in Chinese) , 2008, 51(1): 235-241. |
| [4] | Candes E J. Compressive sampling. The International Congress of Mathematicians. Spain:Madrid, 2006 |
| [5] | Donoho D L. Compressed sensing. IEEE Transactions on Information Theory , 2006, 52(4): 1289-1306. DOI:10.1109/TIT.2006.871582 |
| [6] | Sacchi M D, Ulrych T J, Walker C J. Interpolation and extrapolation using a high-resolution discrete fourier transform. IEEE Transactions on Signal Processing , 1998, 46(1): 31-38. DOI:10.1109/78.651165 |
| [7] | Xu S, Zhang Y, Pham D, et al. Antileakage fourier transform for seismic data regularization. Geophysics , 2005, 70(4): V87-V95. DOI:10.1190/1.1993713 |
| [8] | Zwartjes P M, Sacchi M D. Fourier reconstruction of nonuniformly sampled aliased data. Geophysics , 2007, 72(1): V21-V32. DOI:10.1190/1.2399442 |
| [9] | Herrmann F J, Hennenfent G. Non-parametric seismic data recovery with curvelet frames. Geophysical Journal International , 2008, 173(1): 233-248. DOI:10.1111/gji.2008.173.issue-1 |
| [10] | Lustig M, Donoho D L, Santos J M, et al. Compressed sensing MRI. IEEE Signal Processing Magazine , 2008, 25(2): 72-82. DOI:10.1109/MSP.2007.914728 |
| [11] | Trad D, Ulrych T, Sacchi M. Latest view of sparse radon transform. Geophysics , 2003, 68(1): 386-399. DOI:10.1190/1.1543224 |
| [12] | 张军华, 吕宁, 田连玉, 等. 地震资料去噪方法技术综合评述. 地球物理学进展 , 2006, 21(2): 546–553. Zhang L H, Lü N, Tian L Y, et al. An overview of the methods and techniques for seismic data noise attenuation. Progress in Geophysics (in Chinese) , 2006, 21(2): 546-553. |
| [13] | 周立杰, 王维宏. 叠前含随机噪声地震数据抛物Radon变换法重建. 勘探地球物理进展 , 2007, 30(4): 280–285. Zhou L J, Wang W H. Prestack noisy seismic wavefield reconstruction based on parabolic Radon transform. Progress in Exploration Geophysics (in Chinese) , 2007, 30(4): 280-285. |
| [14] | 仝中飞. Curvelet阈值迭代法在地震数据去噪和插值中的应用研究. 长春: 吉林大学, 2009 . Tong Z F. The study on seismic data denoising and interpolation with curvelet thresholding iterative method (in Chinese). Changchun: Jinlin University, 2009 . |
| [15] | 张军华, 仝兆岐, 何潮观, 等. 在f-k域实现三维波场道内插. 石油地球物理勘探 , 2003, 38(1): 27–30. Zhang J H, Tong Z J, He C G, et al. 3-D seismic trace interpolation in f-k domain. Oil Geophysical Prospecting (in Chinese) , 2003, 38(1): 27-30. |
| [16] | 国九英, 周兴元, 俞寿朋. FX域等道距道内插. 石油地球物理勘探 , 1996, 31(1): 28–34. Guo J Y, Zhou X Y, Yu S P. Iso-interval trace interpolation in F-X domain. Oil Geophysical Prospecting (in Chinese) , 1996, 31(1): 28-34. |
| [17] | 国九英, 周兴元. FK域等道距道内插. 石油地球物理勘探 , 1996, 31(2): 211–218. Guo J Y, Zhou X Y. Iso-interval trace interpolation in F-K domain. Oil Geophysical Prospecting (in Chinese) , 1996, 31(2): 211-218. |
| [18] | Dippe M A Z, Wold E H. Antialiasing through stochastic sampling. Proceedings of SIGGRAPH'85 Conference , 1985, 19(3): 69-78. DOI:10.1145/325165 |
| [19] | Tang G, Shahidi R, Herrmann F J, et al. Higher dimensional blue-noise sampling schemes for curvelet-based seismic data recovery. The 79th SEG Annual Meeting, Houston, Expanded Abstracts , 2009. |
| [20] | Lustig M, Alley M, Vasanawala S, et al. Autocalibrating parallel imaging compressed sensing using L1 SPIR-iT with Poisson Disc sampling and joint sparsity constraints. The ISMRM Workshop on Data Sampling and Image Reconstruction, Sedona '09, 2009 |
| [21] | Donoho D L, Huo X M. Uncertainty principles and ideal atomic decomposition. IEEE Transactions on Information Theory , 2001, 47(7): 2845-2862. DOI:10.1109/18.959265 |
| [22] | Hennenfent G, Herrmann F J. Simply denoise:wavefield reconstruction via jittered undersampling. Geophysics , 2008, 73(3): V19-V28. DOI:10.1190/1.2841038 |
| [23] | Berg E D, Friedlander M P. Probing the Pareto frontier for basis pursuit solutions. SIAM J. on Scientific Computing , 2008, 31(2): 890-912. |
 2010, Vol. 53
2010, Vol. 53

