2. 中国科学院研究生院, 北京 100039;
3. 中国石油塔里木油田分公司勘探开发研究院, 新疆库尔勒 841000
2. Graduate University, the Chinese Academy of Sciences, Beijing 100049, China;
3. Research Institute of Exploration and Development, Tarim Oilfield Company, PetroChina, Korla, Xinjiang 841000, China
逆时偏移的历史可以追溯到1978年Hemon[1]的文章.真正将逆时偏移引入地震勘探这一领域要归功于1983年几位科学家Baysal[2]、McMechan[3]、McMechan[4]和Loewenthal[5]等独立的科研工作,所有这些方法最初都是用做叠后偏移.近年来,由于计算机技术的飞速发展以及对复杂构造油气藏成像要求的提高,逆时偏移重新登上了历史的舞台.目前,逆时偏移技术已经从叠后走向叠前,从二维走向三维[6],从声波方程走向弹性波方程[7],从各向同性介质走向TTI(Tilted Transversely Isotropic,倾斜横向各向同性)介质[8~11].国内方面逆时偏移的研究可追溯到20世纪90年代,这些研究包括有限元法[12~14]、谱元法[15]、有限差分法[16]以及混合法[17].另外,薛东川等[18]采用最大振幅成像条件替代最小走时成像条件;杜启振等[19]将叠前逆时偏移技术应用到横向各向同性介质弹性波多分量数据;刘红伟等[20]用GPU实现了高阶有限差分法逆时偏移,将逆时偏移算法加速了30倍.
计算量大、低频成像噪音以及存储量大是制约叠前逆时偏移应用的三大瓶颈,计算量大的问题笔者已经在文献[20]中介绍(GPU/CPU协同计算高效实现),本文主要探讨低频成像噪音消除以及存储问题.
低频成像噪音主要是由于强反射界面内反射波造成的,噪音的频率一般较低,一种简单的方法是高通滤波,但这种消除往往是不彻底的,并且会破坏波场的有用信息(如盐丘边界信息).低频成像噪音消除的研究从逆时偏移诞生之日起就已经开始,它也是制约逆时偏移应用的一大瓶颈.消除低频成像噪音主要有三种途径:第一,在波场传播过程中消除. Baysal等[21]采用无反射方程,可以消除垂直入射的内反射,但这种方法只能应用于叠后数据,因为无反射方程对于非垂直入射的波反射系数不为零;Loewenthal等[22]对Baysal的方法做出改进,采用大于波长长度的窗函数对模型慢度做平滑,从而消除内反射,这种方法的效果比Baysal的方法效果要好,但是消除了反射的同时也消除了有用的信息,比如棱柱波等信息,会影响逆时偏移成像质量;Robin F Fletcher等[23]采用类似于吸收边界条件的方法,通过在波动方程中引入衰减项,在计算区域产生噪音的位置采用方向衰减的边界条件,压制内反射造成的成像噪音,问题在于,这种方法需要人工交互判断噪音产生的位置,另外衰减边界的引入会衰减掉有用信息.第二,在应用成像条件时去噪.Kwangjin Yoon等[24]利用噪音产生位置炮点与检波点波场传播方向一致性的特点,采用坡印廷矢量成像条件,在成像条件上乘一个方向衰减因子,去噪效果较好,问题在于需要额外计算和存储波场传播矢量,另外,在波场复杂区域,提取波场传播矢量比较困难;Bruno Kaelin等[25]分析了成像噪音与检波点波场的相关性,提出在相关成像条件基础上除检波点的波场,从而达到去噪的目的,这种方法实现起来比较方便,但去噪效果不明显;Faqi Liu等[26]介绍了一种新的成像条件去噪,通过把波场分解成(波数域)上下行波和左右行波(二维情形),运用成像条件时只保留方向相反的波场分量成像结果,可以有效的去噪,问题在于波场分解增加了额外的计算量,对于三维波场需要分解为八个方向分量,另外这种分解可能会损失垂直反射层等有效信息;同年,André Bulcão等[27]提出了一种类似的波场分离去噪方法,原理与上面的方法类似,面临的问题也相似.第三,成像后滤波法去噪.Antoine Guitton等[28]指出传统的滤波方法改变成像结果相位与频谱信息的缺点,采用预测误差滤波器实现最小二乘滤波,在去除成像噪音的同时,波场反射信息得以保存;Zhang等[29]指出拉普拉斯算子滤波相当于成像波场角度域衰减,并且这种操作不需要输出角度域道集.实际操作中,根据不同的问题应该考虑选用不同的去噪方法,另外,应该尽量避免人工干预,避免增加过多的计算量[30].本文提出在叠前对数据进行相位与振幅校正,在成像后运用拉普拉斯算子滤波法消除成像噪音的方法.
波场存储是叠前逆时偏移的另外一个瓶颈.因为炮点波场和检波点波场沿相反的时间方向递推,而应用互相关成像条件时需要相同时刻的波场.这种矛盾迫使叠前逆时偏移过程中,必须将炮点正传波场或者检波点反传波场的传播历史保存下来.这种波场传播的历史往往需要巨大的存储空间,以500×1000×1000的三维空间网格为例,时间方向的步数对地震勘探而言,往往是10000的量级,要保存整个传播历史,单炮数据偏移大约需要20TB的存储量和通讯量,这是目前的计算机硬件无法承受的,必须采取有效的算法减少存储的需要.Ruey-Chyuan Shih等[31]提出了一种分段多步偏移方法,将偏移区域在深度方向按照构造特征划分为几个连续的空间,对每个空间依次偏移;Christopher E Harris等[32]采用类似的方法将成像空间划分为规则的矩形区域,避免人工干预确定边界的复杂性,但这两种方法需要保存分块偏移子空间边界的波场信息,而且增加了I/O和计算时间,并且这两种方法只用在叠后数据上;H Guan等[33]将这种思路用于叠前偏移,而且对于构造相对简单的空间区域,可以选择Kirchhoff积分或者单程波算法来偏移,进一步减少计算量和存储的需求.这种分段多步偏移方法的缺点在于空间的划分要求炮点与检波点在某一个划分的空间内的传播方向单一,这种要求在速度模型未知的情况下是比较困难的,如果空间划分不够合理,无法得到理想的成像结果.William W Symes等[34]提出设置“检查点”(checkpointing)的最优方法.第一次正传时通过设置某些时刻作为“检查点”将波场存储下来,对于非检查点时刻的波场,通过从特定的检查点重新计算这一时刻的波场,选择合适的检查点,可以降低“重算比”(recomputation ratio),问题在于,检查点选得太少,重算比太高,检查点选得过多,所需要存储的临时波场越大,存储问题依然存在;Robert G Clapp等[35]提出随机边界的思想,用计算换存储.本文采用随机边界的思路,借助GPU/CPU协同计算并行实现,优势在于避免了GPU和CPU之间的数据通讯,可以部分弥补增加的计算量.
本文主要包含以下几个部分:首先分析了低频成像噪音的产生机制,提出在叠前对数据进行相位与振幅校正,在成像后运用拉普拉斯算子滤波法消除成像噪音的方法,通过理论模型的测试证明方法的有效性;然后在总结叠前逆时偏移解决波场存储的五种方法的基础上,提出借助GPU/CPU协同计算实现随机边界法逆时偏移,通过盐丘模型的测试证明了方法的可行性.
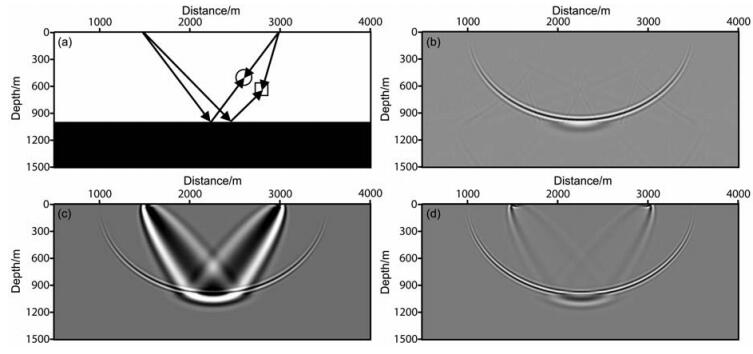
2 去噪 2.1 噪音的产生机制地震叠前逆时偏移低频成像噪音主要是由于强反射界面内反射波造成的.图 1a是一个简单的层状模型,第一层厚度1000 m,速度为3000 m/s.在x=1500 m的位置放炮、3000 m位置接收的一道地震记录走时为0.833 s.图 1b中的椭圆是将这一道地震记录采用单程波方法的偏移结果,椭圆的底部位置是反射界面的位置,将多道和多炮偏移结果相加时相干加强,而椭圆的其他位置相干消除,单程波偏移结果没有低频噪音,这是由于单程波方法限制了波场的传播方向,成像只发生在炮点与检波点波场传播方向相反的位置.与单程波方法不同,逆时偏移会产生低频噪音.
|
图 1 逆时偏移低频成像噪音产生机制 (a)是速度模型, 圆圈位置指示了人射角为90°的噪音产生机制, 方框位置指示了人射角不为90°的噪音机制; (b)是单程波偏移结果, 无噪音; (c)是逆时偏移结果, 含低频噪音; (d)是逆时偏移去噪后的结果. Fig. 1 The generation mechanism of the low frequency band noise in RTM (a) The velocity model.The circle denotes the generation mechanism of noise where the incident angle equals to 90° and the square denotes the generation mechanism of noise where the rncident angle does not equal to 90°; (b) The migration result of one-way wave method without imaging noise; (c) The mgration result of RTM with severe low wave-number imaging noise; (d) The mgration result of RTM after denoise with Laplacian filter. |
根据互相关成像条件:
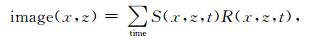
|
(1) |
凡是满足成像条件的位置都可以成像,在本文的例子中,凡是炮点正传时间加上检波点反传时间等于地震道走时0.833s的位置都可以成像,如图 1a中圆圈和方框表示的位置.实际上,在图中箭头线所示的射线整条路径上,成像条件都是满足的,因此会在整条射线路径上成像,如图 1c所示,这就是叠前逆时偏移低频噪音的产生机制.
2.2 拉普拉斯算子去噪拉普拉斯算子的波数域表示如下:
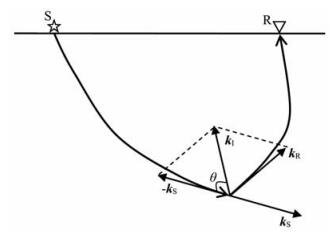
(2)式中的kI是成像域波数矢量,如图 2所示,有如下关系式[36]:
|
图 2 成像域波数矢量计算原理 Fig. 2 The principle of calculating the imaging wavenumber vector |
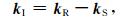
|
(3) |
应用余弦定理可以求得:
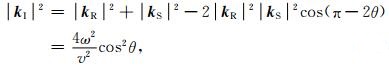
|
(4) |
(4)式中θ是入射角,kR与kS分别是检波点波场与炮点波场的波数矢量.从(4)式不难看出:将拉普拉斯算子作用于逆时偏移成像结果相当于在角度道集上做角度衰减,并且这种方法并不需要输出角度道集,因为拉普拉斯算子是线性操作.图 1a中圆圈位置成像噪音的入射角为90°,根据(4)式,这部分噪音可以被完全消除;方框位置的噪音的入射角度不为90°,只能被部分的消除,如图 1d所示,笔者认为,这种噪音去除结果是合理的,因为方框位置所示的波场传播路径与棱柱波(Prismatic wave)完全一样,如果这种噪音被完全去除,那么棱柱波成像结果也会被去除,逆时偏移的优势便荡然无存.与棱柱波不同的是,这种噪音会在多道叠加时相消,而棱柱波会相干增强.
2.3 叠前处理从(4)式不难看出,拉普拉斯去噪的同时会破坏成像信息的振幅和相位信息.分母的速度平方项比较容易处理,分子中的频率项可以在成像前数据上补偿.
补偿方法有两种:一种直观的方法是将数据变换到频率域,乘上滤波因子,再变换回时间域.另一种方法是在时间域积分,利用以下关系:
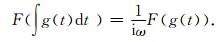
|
(5) |
时间域的方法操作简单,增加的额外计算量可以忽略不计,更重要的是这种方法可以保持波场的局部性;频率域滤波的方法需要做两次Fourier变换,增加了额外的计算量,并且可能会破坏波场的局部性,这是逆时偏移所不希望的.因为逆时偏移是沿时间方向递推,破坏了波场的局部性意味着引入噪音.
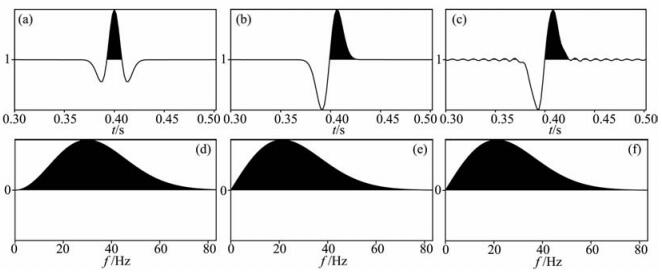
图 3a是一个标准的线性相位Ricker子波,图 3d是它的频谱,图 3b和3c分别是时间域一次积分和频率域滤波(只对带限频率操作)后的子波,图 3e和3f是二者的频谱图,虽然二者频谱类似,但时间域的子波却不同,频率域滤波后的子波的局部性遭到破坏,对逆时偏移是有害的.
|
图 3 Ricker子波测试 (a)原始Ricker子波; (b)-次积分校正后的子波; (c)滤波运算之后的子波; (d)、(e)和(f)分别是前三种子波对应的频谱. Fig. 3 Test on ricker wavelet (a) The original Ricker wavelet; (b) The wavelet after integral modification; (c) The wavelet being filtered in frequency domain; (d), (e) and (f) are the frequency spectral of the three wavelets, respectively. |
下面分别对Marmousi模型和Sigsbee 2a模型做去噪测试.
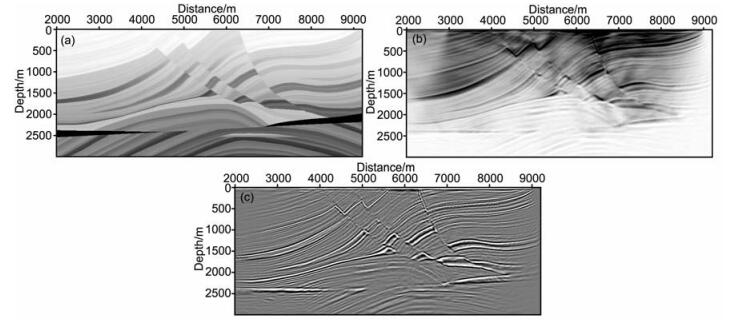
2.4.1 Marmousi模型图 4a是Marmousi偏移速度模型,模型中存在大量的反射界面,逆时偏移之后会在整个剖面上存在低频噪音,如图 4b所示,应用拉普拉斯算子去噪之后的结果如图 4c,低频噪音得到有效压制,断层与界面成像清楚.
|
图 4 MarmouS模型去噪测试 (a)速度模型; (b)去噪之前的逆时偏移结果; (c)去噪之后的逆时偏移结果. Fig. 4 The denoise test on Marmousi model (a) the velocity model; (b) the result of RTM before denoising; (c) the result of RTM after denoising. |
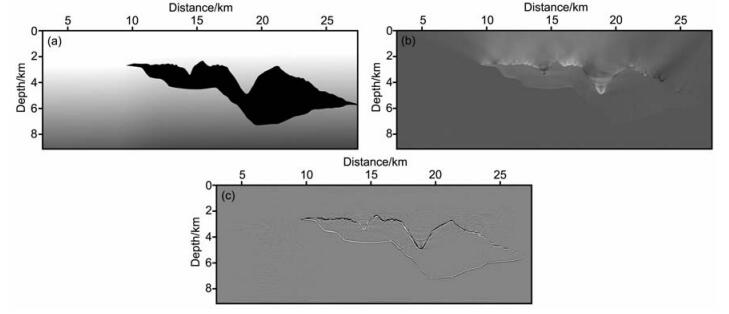
图 5a是Sigsbee 2a偏移速度模型,与Marmousi模型不同,这个偏移速度模型对速度场做了平滑,只在盐丘边界处存在速度间断,相应的,低频噪音主要集中在盐丘边界强反射处,如图 5b所示,这与上文中关于噪音产生机制的分析是一致的,图 5c是应用拉普拉斯算子去噪之后的结果,低频噪音得到有效压制,盐丘边界与盐丘底部散射点成像清楚.
|
图 5 SigSbee 2A模型去噪测试 (a)偏移速度模型; (b)去噪之前的逆时偏移结果; (c)去噪之后的逆时偏移结果. Fig. 5 The denoise test on Sigsbee 2A model (a) The velocity model.(b) The result of RTM before denoising.(c) The result of RTM after denoising. |
从成像条件不难发现,逆时偏移成像需要炮点波场和检波点波场相同时刻的波场.然而与之矛盾的是炮点波场和检波点波场沿相反的时间方向递推,Eric Dussaud等[37]总结了解决这一矛盾的五种途径:
(1) 从t=0开始计算每次成像时需要的与检波点相同时刻的炮点波场,这种方法不存在波场存储问题,但是计算量是O(n2),无法承受;
(2) 把炮点正传历史信息全部存下来,成像时读取相应的信息,计算量是O(n),但存储整个传播历史是目前计算机硬件无法承受的;
(3) 每隔k步存一个波场,中间结果利用插值得到,这种方法的计算量是O(n),存储变为原来的1/k,这也是目前很多商业RTM软件使用的方法,缺点在于插值会损失精度,并且波场存储量依然巨大;
(4) 只在边界存储正传波场信息,反传时作为边界条件重构波场,这种方法增加了一倍的计算量,但存储量大幅度降低到计算机硬件可以承受的地步;
(5) 文献[34]中的设置“检查点”的最优方法.第一次正传时通过设置某些时刻作为“检查点”将波场存储下来,对于非检查点时刻的波场,通过从特定的检查点重新计算这一时刻的波场,选择合适的检查点,可以降低“重算比”.问题在于,检查点选得太少,重算比太高,检查点选得过多,所需要存储的临时波场越大,存储问题依然存在.
本文采用文献[35]中的随机边界的思想,用计算换存储.并将这种方法借助GPU/CPU协同计算并行实现,避免了GPU和CPU之间的数据通讯,可以部分弥补增加的计算量.
3.1 随机边界模型图 6a是带随机边界的速度模型;将炮点置于模型的中央,图 6(b,c,d)分别是t=0.25 s,0.75 s和1.25 s的波场快照;波场遇到随机边界产生漫反射,波前面在1.25 s时已经变成随机噪音,这种随机噪音一方面在成像时不会形成连续的同相轴,另一方面波场反传时可以重构波场有用信息.图 6e是波场从t=1.25 s反传回t=0.25 s时的波场快照;图 6f是正反传波场t=0.25 s时刻的波场差异放大10000倍的结果,二者的差异可以忽略.

|
图 6 随机边界模型测试 (a)带随机边界的速度模型; (b)、(c)、(d)分别是(t=0.25 S, 0.75 3和1.25 S的波场快照; (e)波场反传回, t=0.25 s时的波场快照; (f)正反传波场, t=0.25 s时刻的波场差异放大10000倍的结果. Fig. 6 Random boundary model test (a) The velocity model with random boundaries; (b), (c) and (d) is the wavefield snapshots at t=0.25 s, 0.75 s and 1.25 s; (e) The snapshot of backward propagating wavefield at t=0.25 s; (f) The 10000 magnified difference between (b) and (e). |
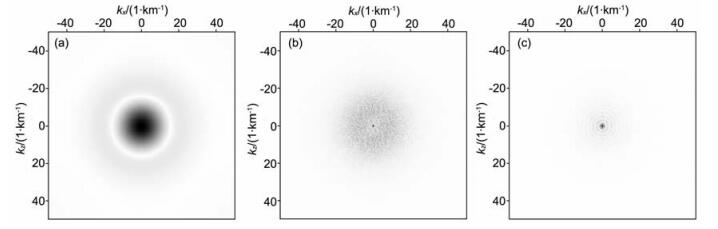
图 7a是初始时刻波场的空间波数谱;图 7b是t=1.25 s时波场的空间波数谱;采用不同的随机边界参数,相同的震源子波信息做了20次试验,图 7c是t=1.25 s时刻20次试验叠加结果的空间波数谱.结果表明,高波数噪音经过叠加后已经有效的去除,只有低波数(长波场)的信息依然存在,这与水波中的“衍射”现象类似.炮域叠前逆时偏移结果是将所有炮的偏移结果累加,这些高波数的噪音可以在累加中被消除.
|
图 7 空间波数谱 (a)初始时刻波场的空间波数谱; (b)t=1.25 s时波场的空间波数谱; (c)t=1.25 s时刻20次试验叠加结果的空间波数谱. Fig. 7 Wavenumber spectral (a) The wavenumber spectral of the wavefield at the original time; (b) The wavenumber spectral of the wavefield at t=1.25 s; (c) The wavenumber spectral of the stacking wavefield from 20 tests at t=1.25 s. |
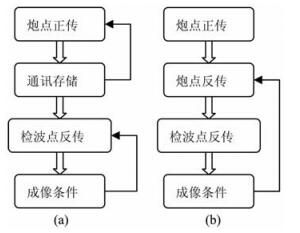
随机边界的引入用计算换存储,炮点正传波场与检波点波场可以同时沿时间反方向传播并成像,不需要存储炮点正传的历史信息.本文借助GPU/ CPU协同计算实现随机边界叠前逆时偏移,图 8a是存储传播历史的GPU/CPU协同计算逆时偏移流程,图 8b是GPU/CPU协同计算随机边界实现逆时偏移的计算流程,从流程图上可以看出,炮点波场正传加反传虽然增加了一倍的计算量,但是可以有效地减少GPU和CPU之间的通讯,所以在计算时间上并不是增加两倍,实测的结果表明,二者的计算时间相差不多.以Sigsbee 2a模型为例,流程一计算单炮的偏移时间为111 s,而流程二的计算时间为136 s,而不是166 s,额外增加的计算量通过减少通讯部分得到弥补.
|
图 8 逆时偏移流程 (a)原始的GPU/CPU协同计算逆时偏移流程; (b) GPU/CPU协同计算随机边界实现逆时偏移的计算流程. Fig. 8 The flow charts of RTM (a) The original flow chart of GPU/CPU collaborative computing RTM; (b) The flow chart of GPU/CPU collaborative computing RTM using random boundary condition. |
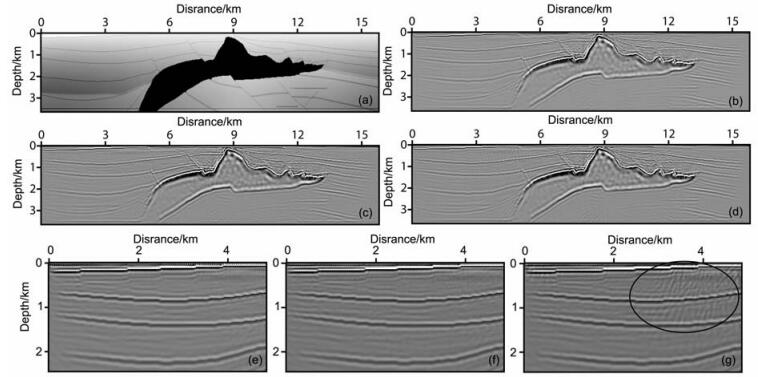
图 9a是二维盐丘速度模型,图 9b是存储炮点传播历史的GPU/CPU协同计算逆时偏移去噪之后的结果;图 9c是借助随机边界的GPU/CPU协同计算逆时偏移结果;图 9d是采用与随机边界相同的计算流程,在边界处采用自由反射边界的GPU/CPU协同计算逆时偏移结果.图 9(e,f,g)分别是图 9(b,c,d)的局部放大结果.通过比较,图 9(g)中的椭圆位置存在严重的噪音,是由于自由反射边界将连续的波场信息反射到成像区域造成的,而借助随机边界的GPU/ CPU协同计算逆时偏移结果与存储传播历史的逆时偏移结果差别很小,证明了随机边界方法的有效性.
|
图 9 二维盐丘模型测试 (a)速度模型; (b)原始的GPU/CPU协同计算逆时偏移结果; (c)借助随机边界的GPU/CPU协同计算逆时偏移结果; (d)自由反射边界GPU/CPU协同计算逆时偏移结果; (e)、(f)、(g)分别是(b)、(c)、(d)的局部放大结果. Fig. 9 Test on 2D sait model (a) The velocity model; (b) The resutt of the traditional GPU/CPU collaborative computing RTM; (c) The resutt of GPU/CPU collaborative computing RTM using random boundary condition; (d) The resutt of GPU/CPU collaborative computing RTM using free reflection boundary condition; (e), (f) and (g) is the partial zoom out of (b), (c) and (d), respectively. |
叠前逆时偏移低频成像噪音主要是由于强反射边界的内反射造成的,本文提出的在叠前对数据进行相位和振幅校正,在成像后运用拉普拉斯算子滤波法消除成像噪音的方法可以完全消除入射角为90°的低频噪音,同时指出入射角小于90°的噪音不能被完全消除的合理性.
借助GPU/CPU协同计算并行实现的随机边界逆时偏移方法,用计算换存储,并且节省了GPU与CPU之间的数据通讯,实验结果表明,采用随机边界方法的偏移结果与直接存储波场的方法得到的结果差别很小,可以用来解决叠前逆时偏移存储量大的问题.
下一步的研究重点是开展GPU集群实现超大规模逆时偏移研究.
致谢对SmartJV提供的Sigsbee模型数据,谨致谢意,感谢李幼铭研究员对本文的指导和帮助.感谢吉星达科技有限公司刘钦和佟小龙对本文的指导和帮助,感谢吉星达科技有限公司允许本文发表.
| [1] | Hemon C. Equations d'onde et modeles. Geophysical Prospecting , 1978, 26: 790-821. DOI:10.1111/gpr.1978.26.issue-4 |
| [2] | Edip Baysal, Dan D Kosloff, John W C Sherwood. Reverse time migration. Geophysics , 1983, 48(11): 1514-1524. DOI:10.1190/1.1441434 |
| [3] | McMechan G A. Migration by extrapolation of time-dependent boundary values. Geophysical Prospecting , 1983, 31: 413-420. DOI:10.1111/gpr.1983.31.issue-3 |
| [4] | Dan Loewenthal, Irshad R Mufti. Reversed time migration in spatial frequency domain. Geophysics , 1983, 48(5): 627-635. DOI:10.1190/1.1441493 |
| [5] | Whitmore N D. Iterative depth migration by backward time propagation. 53rd Annual International Meeting, SEG, Expanded Abstracts , 1983: 827-830. |
| [6] | McMechan G A, Chang W F. 3D acoustic prestack reverse-time migration. Geophysical Prospecting , 1990, 38(7): 737-756. DOI:10.1111/gpr.1990.38.issue-7 |
| [7] | Chang Wen-Fong, George A. McMechan 3-D elastic prestack, reverse-time depth migration. Geophysics , 1994, 59: 597-609. DOI:10.1190/1.1443620 |
| [8] | Zhang Houzhu (James), Zhang Yu. Reverse time migration in 3D heterogeneous TTI media. 78th Annual International Meeting, SEG Expanded Abstracts , 2008, 27: 2196-2200. |
| [9] | Robin P Fletcher, Du Xiang, Paul J. FowlerReverse time migration in tilted transversely isotropic (TTI) media. Geophysics , 2009, 74: WCA179. DOI:10.1190/1.3269902 |
| [10] | Huang Tony, Zhang Yu, Zhang Houzhu, et al. Subsalt imaging using TTI reverse time migration. The Leading Edge , 2009, 28: 448-452. DOI:10.1190/1.3112763 |
| [11] | Zhang Yu, Zhang Houzhu. A stable TTI reverse time migration and its implementation. 79th Annual International Meeting, SEG Expanded Abstracts , 2009, 28: 2794-2798. |
| [12] | 邓玉琼, 戴霆范, 郭宗汾, 等. 弹性波叠前有限元反时偏移. 石油物探 , 1990, 29(3): 22–33. Teng Y C, Dai T F, Kuo John T.. Pre-stack finite element reverse-time migration for elastic waves. Geophysical Prospecting for Petroleum (in Chinese) , 1990, 29(3): 22-33. |
| [13] | 张美根, 王妙月. 各向异性弹性波有限元叠前逆时偏移. 地球物理学报 , 2001, 44(5): 711–719. Zhang M G, Wang M Y. Prestack finite element reverse-time migration for anisotropic elastic waves. Chinese J. Geophys. (in Chinese) , 2001, 44(5): 711-719. |
| [14] | 底青云, 王妙月. 弹性波有限元逆时偏移技术研究. 地球物理学报 , 1997, 40(4): 570–579. Di Q Y, Wang M Y. The study of finite element reverse-time migration for elastic wave. Chinese J. Geophys. (Acta Geophysica Sinica) (in Chinese) , 1997, 40(4): 570-579. |
| [15] | 王童奎, 付兴深, 朱德献, 等. 谱元法叠前逆时偏移研究. 地球物理学进展 , 2008, 23(3): 681–685. Wang T K, Fu X S, Zhu D X, et al. Spectral-element method for prestack reverse-time migration. Progress in Geophysics (in Chinese) , 2008, 23(3): 681-685. |
| [16] | 陈可洋. 基于高阶有限差分的波动方程叠前逆时偏移方法. 石油物探 , 2009, 48(5): 475–478. Chen K Y. High order finite difference prestack reverse time migration. Geophysical Prospecting for Petroleum (in Chinese) , 2009, 48(5): 475-478. |
| [17] | 王山山, 聂勋碧, 邓玉琼. 混合法双程无反射波动方程偏移. 石油地球物理勘探 , 1993, 28(5): 537–542. Wang S S, Nie X B, Deng Y Q. Hybrid migration using two-way nonreflecting wave equation. Oil Geophysical Prospecting (in Chinese) , 1993, 28(5): 537-542. |
| [18] | 薛东川, 王尚旭. 波动方程有限元叠前逆时偏移. 石油地球物理勘探 , 2008, 43(1): 17–21. Xue D C, Wang S X. Wave-equation finite-element prestack reverse time migration. Oil Geophysical Prospecting (in Chinese) , 2008, 43(1): 17-21. |
| [19] | 杜启振, 秦童. 横向各向同性介质弹性波多分量叠前逆时偏移. 地球物理学报 , 2009, 52(3): 801–807. Du Q Z, Qin T. Multicomponent prestack reverse-time migration of elastic waves in transverse isotropic medium. Chinese J. Geophys. (in Chinese) , 2009, 52(3): 801-807. |
| [20] | 刘红伟, 李博, 刘洪, 等. 地震叠前逆时偏移高阶有限差分算法及GPU实现. 地球物理学报 , 2010, 53(7): 1725–1733. Liu H W, Li B, Liu H, et al. The algorithm of high order finite difference pre-stack reverse time migration and GPU implementation. Chinese J. Geophys. (in Chinese) , 2010, 53(7): 1725-1733. |
| [21] | Baysal E, Kosloff D D, Sherwood J W C. A two-way nonreflecting wave equation. Geophysics , 1984, 49: 132-141. DOI:10.1190/1.1441644 |
| [22] | Loewenthal D, Stoffa P A, Faria E L. Suppressing the unwanted reflections of the full wave equation. Geophysics , 1987, 52: 1007-1012. DOI:10.1190/1.1442352 |
| [23] | Robin F Fletcher, Paul Fowler, Phil Kitchenside, et al. Suppressing artifacts in prestack reverse time migration. 75th Annual International Meeting, SEG, Expanded Abstracts , 2005, 24(1): 2049-2051. |
| [24] | Kwangjin Yoon, Kurt J Marfurt, William Starr. Challenges in reverse-time migration. 74th Annual International Meeting, SEG Expanded Abstracts , 2004, 23: 1057-1060. |
| [25] | Bruno Kaelin and Antoine Guitton. Imaging condition for reverse time migration. 76th Annual International Meeting, SEG, Expanded Abstracts , 2006, 25(1): 2594-2598. |
| [26] | Liu Faqi, Zhang Guanquan, Scott A Morton, et al. Reverse-time migration using one-way wavefield imaging condition. 77th Annual International Meeting, SEG, Expanded Abstracts , 2007, 26(1): 2170-2174. |
| [27] | André Bulco, Djalma Manoel Soares Filho, Webe Joo Mansur. Improved quality of depth images using reverse time migration. 77th Annual International Meeting, SEG, Expanded Abstracts , 2007, 26(1): 2407-2411. |
| [28] | Antoine Guitton, Bruno Kaelin, Biondo Biondi. Least-square attenuation of reverse time migration artifacts. 76th Annual International Meeting, SEG Expanded Abstracts , 2006, 25: 2348-2352. |
| [29] | Zhang Yu, James Sun. Practical issues of reverse time migration:true amplitude gathers, noise removal and harmonic-source encoding. CPS/SEG Beijing 2009 International Geophysical Conference & Exposition , 2009. |
| [30] | Matthew H Karazincir, Clive M Gerrard. Explicit high-order reverse time pre-stack depth migration. 76th Annual International Meeting, SEG, Expanded Abstracts , 2006, 25(1): 2353-2357. |
| [31] | Ruey-Chyuan Shih, Alan R Levander. Multigrid reverse-time migration. 58th Annual International Meeting, SEG, Expanded Abstracts , 1988, 7(1): 988-990. |
| [32] | Christopher E Harris, George A McMechan. Using downward continuation to reduce memory requirements in reverse-time migration. Geophysics , 1992, 57(6): 848-853. DOI:10.1190/1.1443298 |
| [33] | Guan H, Kim Y C, Ji J, et al. Multistep reverse time migration. The Leading Edge , 2009, 28: 442-447. DOI:10.1190/1.3112762 |
| [34] | William W Symes. Reverse time migration with optimal checkpointing. Geophysics , 2007, 72(5): SM213-SM221. DOI:10.1190/1.2742686 |
| [35] | Robert G Clapp. Reverse time migration with random boundaries. 79th Annual International Meeting, SEG Expanded Abstracts , 2009, 28: 2809-2813. |
| [36] | Isabelle Lecomte. Resolution and illumination analyses in PSDM:A ray-based approach. The Leading Edge , 2008, 27(5): 650-663. DOI:10.1190/1.2919584 |
| [37] | Eric Dussaud, William W Symes, Paul Williamson, et al. Computational strategies for reverse-time migration. 78th Annual International Meeting, SEG Expanded Abstracts , 2008, 27: 2267-2271. |
 2010, Vol. 53
2010, Vol. 53

