火星是太阳系中的一颗行星,它的磁场是火星探测中的主要物理量之一.火星磁场研究对于火星探索具有重要的科学意义.火星本身到底有没有内禀磁场一直是火星磁层中研究的主要问题,同时也是探测火星的重要目标之一[1, 2].Mars Global Surveyor(MGS)观测结果[3]表明,火星不同于地球,其本身不具有全球性的内禀磁场.但是在火星南半球的局部地区,MGS探测到了磁场大于400 nT的磁场异常区域(简称磁异常),但只在低高度起作用[4].目前一般认为,火星的磁场主要还是它与太阳风相互作用而产生的感应磁场[5].
火星不具有全球的内禀磁场,因此它与太阳风相互作用的方式类似于金星[6],这与地球和太阳风相互作用的方式有很大的差异.在火星上,来自太阳的强紫外辐射使上层大气电离,同时形成热的中性大气层延伸至太阳风.由热压和磁压组成的电离层压强与太阳风流的压强相平衡.进入太阳风的中性大气被电离,补充到太阳风流,使太阳风速度减弱.在这种情况下,绕火星的磁场流减速运动导致了磁力线向障碍物方向的拖拽,在磁尾形成了长长的尾巴,垂直于太阳风的磁场由于这种相互作用呈现弯曲.火星及其周围的大气相对于太空等离子体的作用像一个障碍物体,火星周围的磁力线就披挂在火星这个障碍物上[7].
本文从我们提出的模型出发,没有全球内禀磁场的火星与太阳风相互作用,会在其导电的电离层上产生感应电流.根据电流是闭合的这一特性可知,火星电离层上的电流、磁层顶上的电流以及磁尾电流片上的电流这三种电流体系满足以下的关系:磁层顶上的总电流等于电离层上的总电流与磁尾电流片上的总电流之和.这几种电流产生的磁场和太阳风磁场一起构成了火星周围的感应磁场.由毕奥-萨伐尔定理,通过数值计算,得到火星磁场强度,利用自编的磁力线跟踪程序得到火星磁力线分布,最后得出结果并加以讨论.
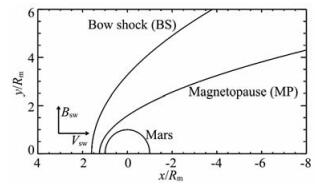
2 火星感应磁场模型 2.1 火星磁层结构及其相关的参数 2.1.1 火星-太阳轨道坐标系火星赤道面上的磁层结构[8]如图 1所示,其坐标系的建立如下:以火星为中心,x轴的方向由火星指向太阳,y轴的方向与火星公转轨道的速度方向相反,称之为火星为中心的太阳轨道坐标系(Mars-centered Solar Orbital Coordinate System,简称MSO)[9].太阳风速度VSW的方向与x轴正方向相反.太阳风磁场BSW在x-y平面内,其方向与y轴正方向相同,在这里我们考虑太阳风磁场BSW与太阳风速度VSW垂直的情况,即帕克螺旋角取90°,其大小为BSW=4 nT.
|
图 1 火星赤道面上的磁层结构 Fig. 1 Magnetospheric structure in the Martian equatorial plane |
火星与太阳风相互作用,在火星周围产生感应电场,表示为
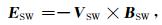
|
(1) |
导电的火星电离层在感应电场的作用下产生感应电流,表示为
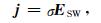
|
(2) |
σ是火星电离层上的电导率.电离层上的感应电流沿火星的经线方向由南向北流动.为了计算的方便,用十六根离散的线电流来等效代替火星电离层上感应的电流,这十六根离散的线电流的形状是半圆形,半径为1.03 Rm,Rm是火星的半径,Rm=3397 km.它们沿火星不同的经线分布在电离层上,每根离散的线电流强度大小相等,用I1表示,大小为I1=87135A.
2.1.3 火星磁尾电流片电流分布
由于火星与地球不同,自身不具有全球的内禀磁场,它的磁尾电流片位于子午面内(x-z平面内).文献[10]以及恰当的假设,不考虑火星磁尾电流片的厚度,宽度为13 Rm,离火星地面的高度为3 Rm,其上的电流连续均匀分布,电流密度用i2表示,大小为i2=0.15 A/m.总电流强度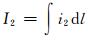
对于火星磁层顶,其在x-y平面内的形状[11]可用抛物线来表示,即
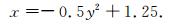
|
(3) |
火星磁层顶上的电流分布分两个部分:向阳面和背阳面.对于向阳面的磁层顶上电流分布,为了计算的方便,向阳面的磁层顶上电流离散分布,用七根离散的线电流来等效代替向阳面的磁层顶上电流分布,这七根离散的线电流分别位于子午面内以及和子午面成30°、45°和60°角的平面内,它们的形状是半径不同的半圆.每根线电流强度大小相等,用I3表示,大小为I3=99600A.
对于背阳面的磁层顶,其形状是一个空心的圆柱,圆柱的半径随着远离火星而越来越大.背阳面的磁层顶上电流连续均匀分布,其与磁尾电流片上的电流构成回路,在磁尾形成两个半θ形电流分布.由火星磁场分布的特点可知,这两个半θ形电流并不与x轴垂直,与x轴成一定的角度[12].在本文中,这个角度为30°.背阳面的磁层顶两个半θ形电流具体的形状和位置表示如下:
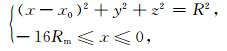
|
(4) |
上述(4)式中,x0是半θ形电流所在圆心的坐标,R是半θ形电流的半径,这两个参数都是变化的.背阳面的磁层顶两个半θ形电流均匀分布,电流密度大小相等,用i4表示,大小为i4=0.0682 A/m.每部分的电流强度是
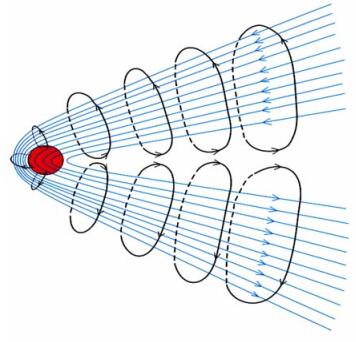
用两根线电流连接电离层上的电流和磁层顶上的电流,这两根线电流的大小一样,用I5表示,大小为I5=16I1.该两根电流位于z轴上,方向与z轴正方向相同,它们具体的位置分别位于1.03 Rm≤z≤1.25 Rm和-1.25 Rm≤z≤-1.03 Rm处.上述几种电流体系分布的示意图如图 2,其中黑线表示电流,蓝线表示磁力线.
|
图 2 火星磁层中电流(黑线)和磁场(蓝线)分布示意图 Fig. 2 Schematic diagram of current (black lines) and magnetic field (blue lines) distribution in the Martian magnetosphere |
火星周围磁场产生的原因和拓扑结构与地球不同,地球磁场产生的原因是地球内部的发电机原理,地球本身具有内禀磁场(主要部分为偶极子);火星的内部发电机已经停止,其磁场是由于火星与太阳风相互作用产生的感应磁场,磁场是披挂在火星表面上的[13].
根据电动力学可知,两边磁场(大小,方向)发生变化的边界,必有与磁场变化相垂直的电流分布.地球向阳面的磁层顶电流可以围绕(南北)极尖区在磁层顶闭合,是因为在该电流下面地球磁场由于偶极子拓扑结构汇聚到极尖区而与磁层顶电流相垂直.而在火星周围,没有这样的磁场拓扑结构,磁层顶电流不可能自身在磁层顶闭合,磁层顶电流必须与电离层顶电流或跨尾电流相连接,即电流必须包裹火星的磁力线.
考虑到电流始终包络磁力线这一性质,火星有这样的磁场分布,必须有相应的电流分布.至于这些电流的具体分布,则根据火星电离层和磁层顶的位置而定,同时考虑电流是闭合的这一特性.对于上述几种电流的大小,有些为了计算的方便,用等效的电流来代替.
火星周围空间分布中,存在一个磁场堆积区[14],经过此堆积区,磁场大小剧烈地增加,因此磁场的梯度很大.火星磁层中的带电粒子会产生漂移,并且电子与离子沿着相反的方向漂移,引起电荷分离产生漂移电流.本文认为火星磁层中的电子和离子沿相反方向漂移是产生磁层顶电流的原因.
3 计算原理 3.1 磁场强度公式在上述火星磁层中几种电流体系分布的情况下,利用毕奥-萨伐定理可得到空间任何一点r(x,y,z)磁场强度的表达式如下:
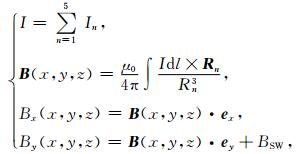
|
(5) |
在上述磁场强度的表达式中,Rn是火星磁层中电流体系的源点rn′(x′,y′,z′)到空间任何一点r(x,y,z)的方向矢量,即Rn=r-rn′,下标n表示火星磁层中不同的电流系分布,μ0=4π×10-7 N·A,是真空磁导率.ex是x方向的单位矢量,ey是y方向的单位矢量.
3.2 数值方法上述磁场强度表达式中的积分是对火星磁层中的电流进行的.由于磁场表达式是积分形式,求解析解非常困难,因而只能通过数值求解.在求数值解的过程中,采用的是梯形法:
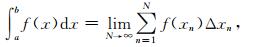
|
式中每一个小梯形的区间宽度为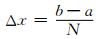
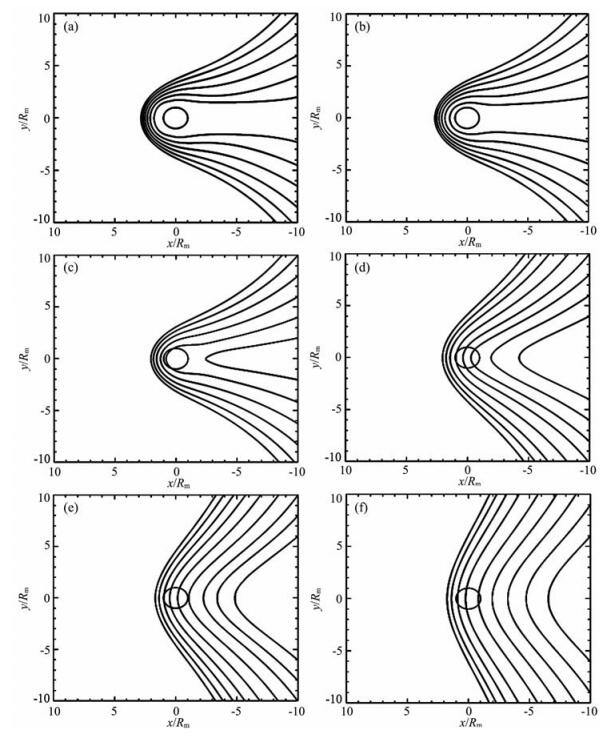
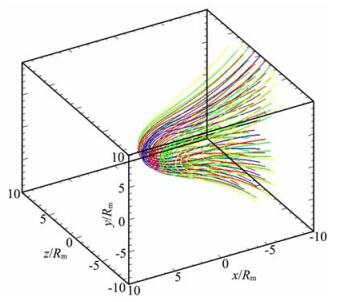
根据以上火星磁场强度的表达式以及具体的数值方法,利用自编的磁力线跟踪程序,分别得到火星赤道面(z=0),z=±Rm、z=±2Rm、z=±3Rm、z=±4Rm和z=±5Rm平面上的磁场分布,如图 3所示.图 4是火星周围磁场分布.通过这几张图我们可以发现,火星周围的磁场拓扑与地球磁场结构有着明显的不同,原因在于其本身不具有内禀磁场,而地球本身具有偶极场.由于地球具有偶极场,磁压与太阳风动压相平衡,在地球周围形成磁层顶,并且地球日下点距地球表面较远,地球偶极场充当保护伞的作用,避免太阳风直接与地球大气层和电离层发生相互作用.火星本身不具有内禀磁场,它周围的磁场是由于火星的电离层直接与太阳风作用而感应产生的,即火星导电的电离层处在运动着的太阳风磁场中,电离层内产生感应电流,此电流产生磁场.火星电离层的高度很低,离火星地面大约100 km[15],火星向阳面磁场不能有效地阻挡太阳风的动压,所以火星磁层顶的日下点距火星表面很近[16],大约0.25 Rm左右.从图中可以看出,火星周围的磁力线在太阳风的作用下,披挂在火星表面上,形成一个开放的磁尾.模型得到的结果与观测和用其他方法得到的结果符合的较好.
|
图 3 赤道(z=0)(a)、z=±Rm(b)、z=±2Rm(c)、z=±3Rm (d)、z=±4Rm (e)、z=±5Rm (f)平面上的磁场分布 Fig. 3 Distribution ofraagnetic field on the Martian equatorial plane (a)、the plane z=±Rm(b)、the plane z=±2Rm (c)、the plane z=±3Rm(d)、the plane z=±4Rm(e) and the plane z=±5Rm(f) |
|
图 4 火星的磁场分布 Fig. 4 Distribution of Martian magnetic field |
本文通过构建一个电流模型来得到火星的磁场分布.太阳的紫外辐射导致火星周围大气层发生电离,在太阳风感应电场的作用下,火星电离层上出现感应电流.利用电流本身连续的性质以及卫星的观测数据,合理假设火星磁层顶上的电流以及火星磁尾电流片上的电流和电离层上的电流分布.利用毕奥-萨伐尔定理求得火星周围磁场强度,最后利用自编的磁力线跟踪程序得到火星周围的磁力线分布.
对于火星赤道面上的磁场分布,利用我们的物理模型得到的结果与卫星观测的结果以及用其他方法得到的结果符合的较好.但是这种模型是很粗糙地描述了火星磁场结构,这种物理模型有自身的缺陷与不足.目前的工作是初步的,需要进一步改进模型中的各种参数.以下是今后工作需要解决的问题:(1)为了计算的方便,本文中用十六根离散的线电流等效地代替了火星电离层上的电流分布,在以后的工作中,根据观测卫星数据将进一步细化火星电离层上的电流分布.(2)磁层顶向阳面上的电流分布,本文用七根离散的线电流来等效代替,在今后的工作中,结合观测资料进一步细化其分布.(3)本文中我们忽略磁层顶和磁尾电流片的厚度,今后将考虑其厚度.(4)本文我们假设太阳风磁场的方向与太阳风速度方向垂直,以后将讨论不垂直的情况.
| [1] | 史建魁, 刘振兴. 火星磁层探测结果的分析研究. 地球物理学进展 , 1996, 11(4): 77–86. Shi J K, Liu Z X. Analysis and research of detective results about Martian magnetosphere. Progress in Geophysics (in Chinese) , 1996, 11(4): 77-86. |
| [2] | Slavin J A, Schwingenschuh K, Riedler W, et al. The solar wind interaction with Mars:Mariner-4, Mars-2, 3, 5, and Phobos-2 observations of bow shock position and shape. J. Geophys.Res. , 1991, 96(A7): PAGES 11235-11241. DOI:10.1029/91JA00439 |
| [3] | Acuna M H, Connerney J E P, Wasilewski P, et al. Magnetic field and plasma observations at Mars:Initial results of the Mars Global Surveyor Mission. Science , 1998, 279(5357): 1676-1680. DOI:10.1126/science.279.5357.1676 |
| [4] | Brain D A, Bagenal F, Acuna M H, et al. Martian magnetic morphology:Contributions from the solar wind and crust. J Geophys.Res. , 2003, 108(A12). |
| [5] | Luhmann J G, Brace L H. Near-Mars space. Rev. Geophys , 1991, 29(2): 121-140. DOI:10.1029/91RG00066 |
| [6] | Luhmann J G. The solar wind interaction with Venus. Space Sci. Rev. , 1986, 44(3): 241-306. |
| [7] | Crider D, Brain D, Acuna M H, et al. Mars global surveyor observations of solar wind magnetic field draping around Mars. Space Sci. Rev. , 2004, 111(1): 203-221. |
| [8] | Esa Kallio, Hannu Koskinen. Ion acceleration in the Martian plasma environment. Adv.Space Res. , 1998, 21(4): 573-582. DOI:10.1016/S0273-1177(97)00966-6 |
| [9] | Kallio E. An empirical model of the solar wind flow around Mars. J Geophys.Res. , 1996, 101(A5): 11333-11147. |
| [10] | Halekas J S, Brain D A, Lillis R J, et al. Current sheets at low altitudes in the Martian magnetotail. Geophys.Res.Lett. , 2006, 33: L13101. DOI:10.1029/2006GL026229 |
| [11] | Kallio E, Koskinen H. A test particle simulation of the motion of oxygen ions and solar wind protons near Mars. J Geophys.Res. , 1999, 104(A1): 557-579. DOI:10.1029/1998JA900043 |
| [12] | Yingjuan M, Andrew F Nagy, Igor V Sokolov, et al. Three-dimensional, multispecies, high spatial resolution MHD studies of the solar wind interaction with Mars. J Geophys.Res. , 2004, 109. |
| [13] | Schwingenschuh K, Riedler W, Zhang T L, et al. The Martian magnetic field environment:Induced or dominated by an intrinsic magnetic field?. Adv. Space Res. , 1992, 12(9): 213-219. DOI:10.1016/0273-1177(92)90333-S |
| [14] | Bertucci C, Mazelle C, Crider D H, et al. Magnetic field draping enhancement at the Martian magnetic pileup boundary from Mars global surveyor observations. Geophys.Res.Lett. , 2003, 30(2): 1099. DOI:10.1029/2002GL015713 |
| [15] | Shinagawa H. The ionospheres of Venus and Mars. Adv.Space Res. , 2004, 33(11): 1924-1931. DOI:10.1016/j.asr.2003.06.028 |
| [16] | Vignes D, Mazalle C, Rme H, et al. The solar wind interaction with Mars:locations and shapes of the bow shock and the magnetic pile-up boundary from the observations of the MAG/ER experiment onboard Mars Global Surveyor. Geophys.Res.Lett. , 2000, 27(1): 49-52. DOI:10.1029/1999GL010703 |
 2010, Vol. 53
2010, Vol. 53


