地磁场及其长期变化是地磁学的重要研究内容[1~3].为描述全球地磁场及其长期变化,1968年国际地磁学与高空物理学协会(IAGA)发布了1965.0年代的国际地磁参考场(IGRF),随后IAGA给出了每5年的IGRF[4~10].地磁场及其长期变化具有区域特征,IGRF是国际地磁参考场,不能精确描述区域地磁场及其长期变化.为此,各国学者应用不同的分析方法,得到了准确表述的各国区域地磁场及其长期变化[11~21].我国学者分析与研究了中国地区的地磁场及其长期变化,获得了有意义的结果[22~31].
地磁长期变化是指地磁场随时间的缓慢变化,经典的描述是地磁场各分量年均值的时间变化.以国际地磁参考场(IGRF)为代表的研究方法是通过建立地磁长期变化的数学模型,描述并分析地球主磁场在空间和时间上的变化过程.建立地磁长期变化模型涉及如下问题:其一,如何从观测数据中准确地分离出地球主磁场的时间变化,因为在地磁观测数据中地磁主磁场、静态地壳场、外源场和内部感应场是相互叠加的,即便是地磁分量的年均值,其中也不同程度地包含有除主磁场外的其他成分;其二,使用何种数学方法建立地磁长期变化模型;其三是所建立的地磁长期变化模型的合理性、准确性和分辨率.
对地磁场的研究,尤其是对主磁场的研究离不开地磁长期变化模型.地磁场及其测量的实际应用,如导航、矿产勘探、地震和火山活动研究等,均需要准确的、高分辨率的地磁长期变化模型[32, 33].对野外地磁测量数据进行长期变化改正时,仍然需要适用的地磁长期变化模型.
地磁台站的观测数据对地磁长期变化的分析研究是十分重要的.中国境内现代科学意义上的固定地磁台站观测始于徐家汇验磁台(佘山地磁台的前身,1874年正式产出地磁观测数据)[34].1957~1958年第一届国际地球物理年期间,中国科学院建立了北京白家疃等7个地磁台,于20世纪50年代末期开始正式观测.1978年国家地震局成立以后,除负责上述台站的运行外,陆续建立了满洲里等数十个地磁台,于20世纪80年代中后期正式观测[35].这些台站构成了中国地区地磁观测的基本台网.本文使用2000年1月1日至2004年12月31日中国地区34个台站的地磁日均值,采用几种方法计算了各台站的地磁年变率,并建立了相应的“2000.0~2005.0年代中国地区地磁长期变化泰勒多项式模型”和“2000.0~2005.0年代中国地区地磁长期变化曲面样条模型”,讨论了不同方法所获得的各台站地磁年变率之间的差异、不同的长期变化模型之间的差异及其与IGRF2005-SV之间的异同之处.
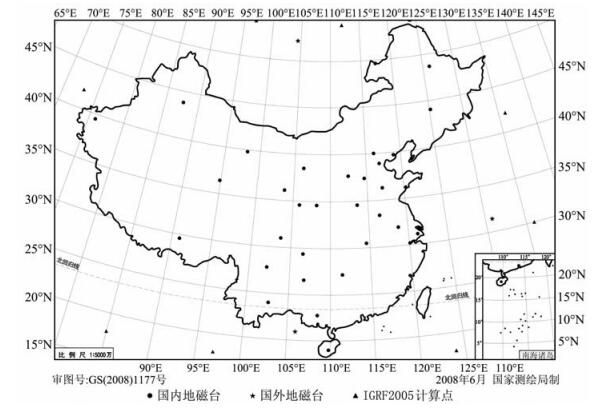
2 地磁台站数据采用2000年1月1日至2004年12月31日中国地区34个台站地磁三分量连续的地磁日均值,作为分析研究的基本数据.这三分量分别为地磁总强度F、磁偏角D与磁倾角I.图 1为地磁台站的分布.从图 1可以看出,上述地磁台站的空间分布是不均匀的,尤其是内蒙古、青海、西藏和新疆等地区的台站甚为稀疏.这种台站分布的不均匀性与西北地区台站稀疏将对地磁长期变化的分析研究产生不利的影响.因此,在调整与改造中国地磁台网时,应当适当增加西北地区的台站,注意并调整台站的均匀布局.
|
图 1 地磁台站的分布 Fig. 1 Distribution of the geomagnetic observatories |
为降低地磁模型计算的边界效应,应用了周边国家三个台站的地磁数据与根据IGRF-10模型所得到的15个测点的地磁场值[29].这三个台站与15个测点的位置如图 1所示.
本研究没有应用地磁重复测量资料,这是因为在2000~2005年间,没有重复的地磁测量数据.实际上,2000年以前是由原中国科学院地球物理研究所承担中国地磁图及其地磁测量[27, 28].从2001年起,在中国科技部与中国地震局的资助下,中国地震局地球物理研究所承担了中国地磁图及其地磁测量[25].由于2000年以前地磁测点标识的丢失、测点环境变化等原因,2002~2004年中国地震局地球物理研究所重新建立了中国地区1119个新的地磁测点[36].这是一种特殊情况.今后的地磁测量工作将获得重复测量的地磁数据,以供相关的分析研究使用.
3 通日平均年变率、静日平均年变率和拟合年变率的计算与分析应用中国地区34个台站各地磁分量的全部有效的日均值(剔除受到局部环境干扰的观测数据),计算2000~2004年各台站的年均值逐年差值的平均值,并将该平均值称为地磁通日平均年变率.同样,根据这些台站各地磁分量的全部静日日均值计算出2000~2004年各台站的年均值逐年差值的平均值,将此平均值称为地磁静日平均年变率.
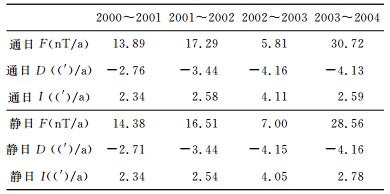
表 1为成都台的地磁年变化.从表 1可见,在2000~2004年成都台的地磁逐年变化有显著差异,而且通日日均值的平均年变和静日日均值的平均年变具有相同的差异形态,但静日日均值的平均年变率的逐年变化的差异相对小些.
|
|
表 1 成都台(CDP)的地磁年变化 Table 1 Geomagnetic annual variation at the observatory CDP |
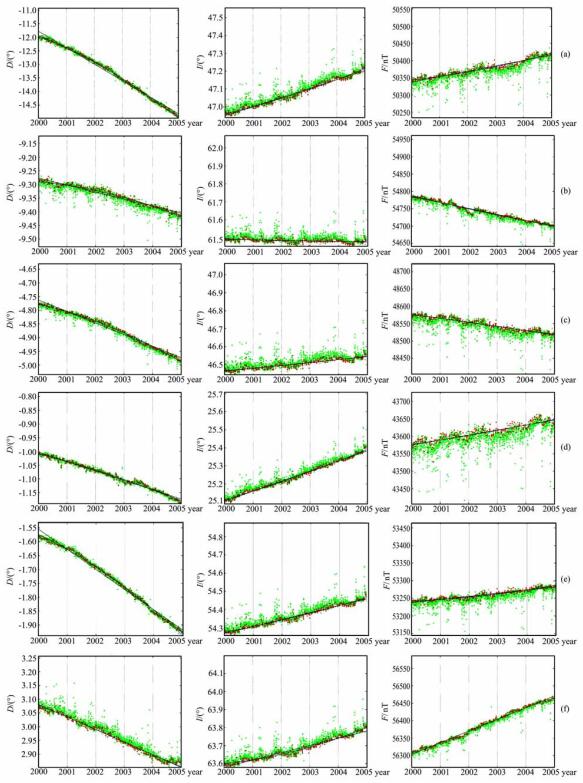
为分析中国地区地磁时空变化,绘制了2000~2005年各台站的地磁变化.限于篇幅,经过分析比较,在34个台站中仅选了7个台站,将这7个台站的地磁变化示于图 2.这7个台站基本按照中国边界的东南西北及中央选取,所以它们的地磁变化具有典型性与代表性.图 2为这7个台站的地磁日均值的时间变化及线性拟合结果.图 2a为成都台各地磁分量的日均值及拟合结果,从图 2a的时间分布看,2003年地磁总强度F的观测值存在明显的偏低异常,因此造成了2002~2003年F年变率的偏小和2003~2004年F年变率的偏大.而2004年上半年磁倾角I的观测值明显存在偏低异常,使得2003~2004年I年变率偏小.仔细对比周边的兰州(LZH)、天水(TSY)、重庆(COQ)、格尔木(GLM)和西昌(XIC)等台站,都发现了类似的日均值分布的异常形态,只是异常的幅度没有成都台那样显著.由此可见,这种异常不是孤立的,而是地磁场的一种区域异常现象,表现为叠加在主磁场正常的长期变化上、视周期较短的时间变化.这种异常现象的存在意味着如果简单地以地磁场观测值的平均年变率-无论是通日日均值还是静日日均值-来描述地磁主磁场的长期变化,会带来相当的误差.为此,必须采用适当的方法从台站的地磁观测日均值数据中提取出地磁长期变化量.
|
图 2 各台站的地磁偏角D、磁倾角I、总强度F的日均值及其拟合结果 图中的红点为静日的日均值, 绿点为非静日的日均值, 黑线为其拟合结果.(a)成都台(CDP), (b)长春台(CNH), (c)佘山台(SSH), (d)琼中台(QGZ), (e)兰州台(LZH), (f)乌鲁木齐台(WMQ), (g)拉萨台(LSA). Fig. 2 The diurnal means and their fitting results of geomagnetic declination D, inclination I and total intensity F In the figure, the red point represents the diurnal means for quiet day, the green point represents the diurnal means.for non-quiet day, the black line represents the itting results.(a) the Observatory CDP, (b) the Observatory CNH, (c) the Observatory SSH, (d) the Observatory QGZ, (e) the Observatory LZH, (f) the Observatory WMQ, (g) the Observatory LSA. |
对2000年1月1日至2004年12月31日期间各台站的地磁分量全部静日日均值随时间变化进行了线性拟合,将所获得的拟合直线的斜率称为地磁静日均值线性拟合年变率.同样,对同期各台站的地磁分量的全部静日均值随时间变化进行了二次曲线拟合,并计算拟合曲线在2000年1月1日至2004年12月31日期间变化率的平均值,将该值称为地磁静日均值二次拟合平均年变率.表 2给出了具有代表性的15个地磁台的四种年变率:通日平均年变率A,静日平均年变率B,静日线性拟合的平均年变率C和静日二次拟合的平均年变率D.从表 2与图 2可见,各台站地磁分量的日均值包含非常丰富的外源变化场和内部感应场的成分,在非静日日均值上表现明显.这种外源变化场和内部感应场成分的空间分布是非常复杂的,例如,拉萨台、兰州台和乌鲁木齐台D日均值之间存在明显差异,而长春台、佘山台和琼中台F日均值之间亦有明显差异,拉萨台、兰州台和成都台I日均值之间也有明显差异.而且,在同一台站不同地磁分量的分布存在明显差异,F扰动幅度明显比D的扰动幅度大;在时间域上的分布是非常不均匀的,例如I在2004年的扰动幅度明显比其他年份大.此外,从图 2可见,2000~2001年成都台D、兰州台D与拉萨台I偏离线性拟合,这种现象是与相关台站所在地区的地下介质的电磁性质、地质构造、地壳构造活动等因素有关.
|
|
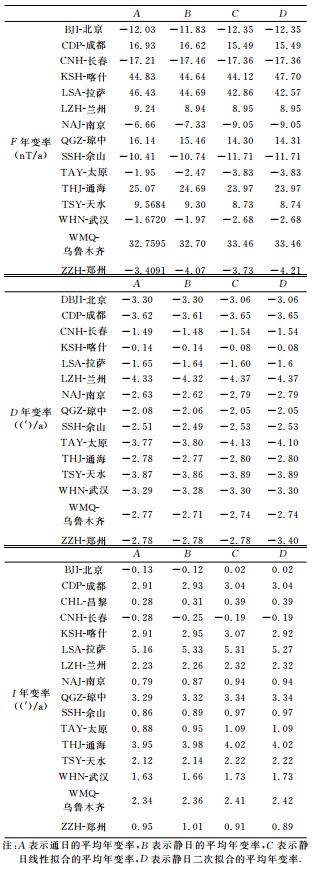
表 2 各台站的地磁年变率 Table 2 Geomagnetic annual variation rates at various observatories |
在有的台站,地磁日均值随时间的变化呈现明显的非线性,尤其拉萨台的D、I和F存在很明显的非线性.各台站的通日平均年变率、静日平均年变率、静日均值线性拟合的平均年变率和静日均值二次拟合的平均年变率之间存在着差异,这一差异在有些台站表现显著,其中喀什、拉萨、太原和南京台的F年变率,北京、喀什和郑州台的I年变率,以及北京、昌黎和郑州台的D年变率,均存在明显差异.相比较而言,中国地区34个地磁台的静日均值线性拟合的年变率空间分布较通日平均年变率和静日平均年变率的空间分布更为均匀.
在日均值分布非线性显著的地磁台附近,如喀什台的F、郑州台的D和静海台的I,地磁静日均值二次拟合的平均年变率空间分布较静日均值线性拟合的年变率空间分布更为均匀.因此,应用地磁静日均值二次拟合的平均年变率描述2000.0~2005.0年代中国地区的地磁长期变化是比较合理的.
4 2000.0~2005.0年代中国地区地磁长期变化模型应用曲面Spline方法描述地磁长期变化的数学表达如下:
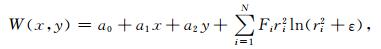
|
(1) |
式中W(x,y)表示坐标点(x,y)的地磁场,ri2=(xi-x)2 +(yi-y)2,a0,a1,a2,Fi是待定系数,由下列方程组求出:
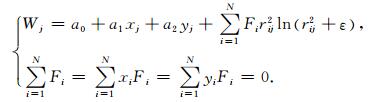
|
(2) |
曲面Spline模型共有(N+3)个系数,N为数据点个数,ε为控制曲面曲率变化的收敛因子.
应用泰勒多项式描述地磁长期变化的数学表达为
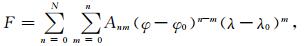
|
(3) |
式(3)中的Anm为泰勒多项式的系数,N为泰勒多项式的截断阶数,φ和λ分别为地磁台站的纬度和经度,单位为rad,φ0和λ0分别为泰勒多项式展开原点的纬度和经度,单位为rad.F表示各地磁分量.
本文使用了空间分布相对均匀的地磁静日均值二次拟合的平均年变率来建立“2000.0~2005.0年代中国地区地磁长期变化泰勒多项式模型”和“2000.0~2005.0年代中国地区地磁长期变化曲面样条模型”.为降低地磁模型计算的边界效应,还应用了日本KNY台、俄罗斯IRT台和越南PHU台的地磁数据及15个点的IGRF2005-SV计算值(图 1).建立模型时的计算区间为:18°N~54°N,73°E~136°E,泰勒多项式模型的计算原点为:36.0°N,104.5°E,曲面样条模型的ε取为10-3.
在进行地磁模型计算时,面临的主要技术问题是截断阶数的确定.通常是试算若干截断阶数的模型,根据对各模型计算值和实际观测值的最小二乘残差及相应的边界畸变的综合评价,最终确定采用的截断阶数[29].在建立泰勒多项式模型时,截断阶数N分别为1~8进行了模型计算,通过对模型收敛误差和模型空间分布的合理性综合判断,最终确定截断阶数N取为3.在建立曲面样条模型时,曲面曲率控制因子ε分别取10-2~10-5进行了模型计算,最终确定曲面样条模型的收敛因子ε取为10-3 [31],模型共有55个系数.
经过上述模型计算,得到2000.0~2005.0年代中国地区地磁长期变化的泰勒多项式模型与曲面样条模型(图 3、4和图 5),这两个模型的系数分别列于表 3与表 4.
|
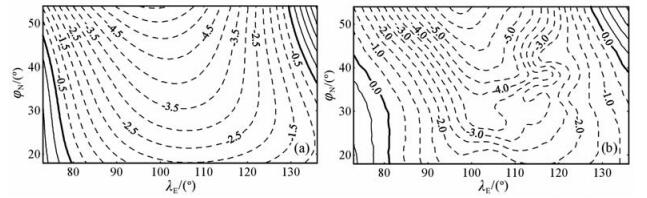
图 3 2000.0~2005.0年代中国地区磁偏角D长期变化的泰勒模型(a)和曲面样条模型(b), 等变线单位:(′)/a 图中实线表示正值, 虚线表示负值. Fig. 3 Taylor model (a) and spline model (b) of secular variation of the declination D in China for 2000.0~2005.0, unit:(′)/a In the figure, the solid line denotes the positive value and the dashed line denotes the negative value. |
|
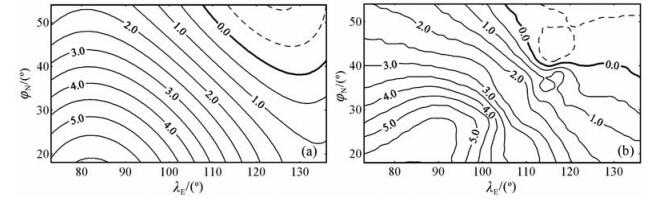
图 4 2000.0~2005.0年代中国地区磁倾角I长期变化的泰勒模型(a)和曲面样条模型(b), 等变线单位:(′)/a 图中实线表示正值, 虚线表示负值. Fig. 4 Taylor model (a) and spline model (b) of secular variation of the lnclination I in China for 2000.0~2005.0, unit:(′)/a In the figure, the solid line denotes the positive value and the dashed line denotes the negative value. |
|
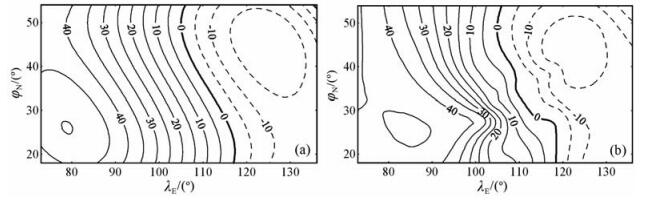
图 5 2000.0~2005.0年代中国地区地磁总强度F长期变化的泰勒模型(a)和曲面样条模型(b), 等变线单位:nT/a 图中实线表示正值, 虚线表示负值. Fig. 5 Taylor model (a) and spline model (b) of secular variation of the total intensity F in China for 2000.0~2005.0, unit:nT/a In the figure, the solid line denotes the positive value and the dashed line denotes the negative value. |
|
|
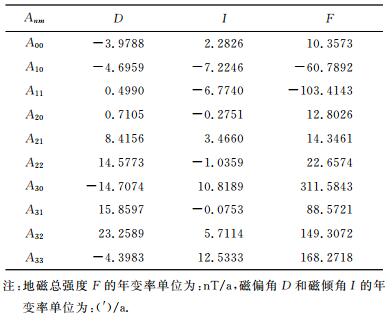
表 3 2000.0~2005.0年代中国地区地磁长期变化的曲面样条模型系数 Table 3 Coefficients of the splinemodel of geomagnetic secular variation inChina for 2000.0~2005.0 |
|
|
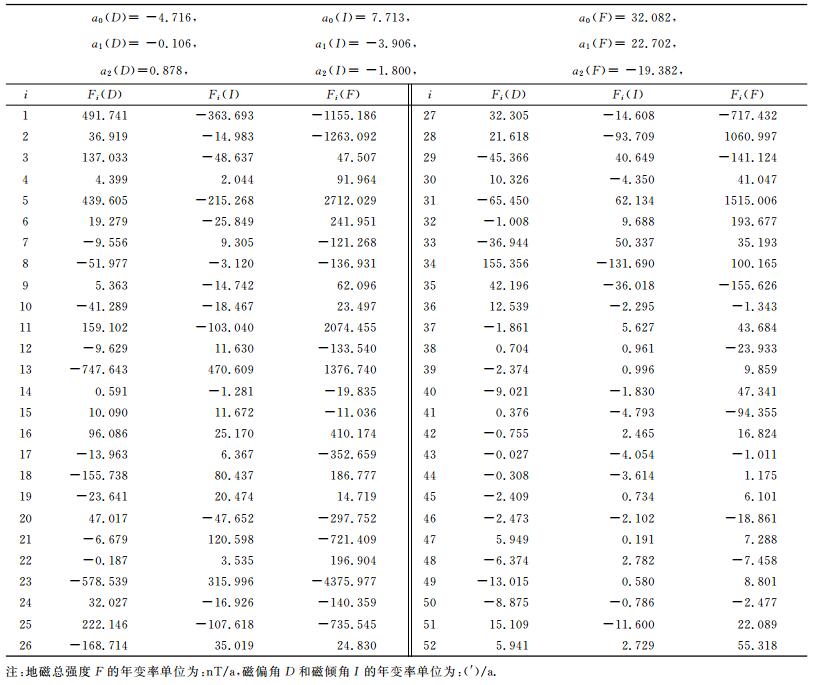
表 4 2000.0~2005.0年代中国地区地磁长期变化的泰勒多项式模型系数 Table 4 Coefficients of the Taylor polynomial model of geomagnetic secular variation inChina for 2000.0~2005.0 |
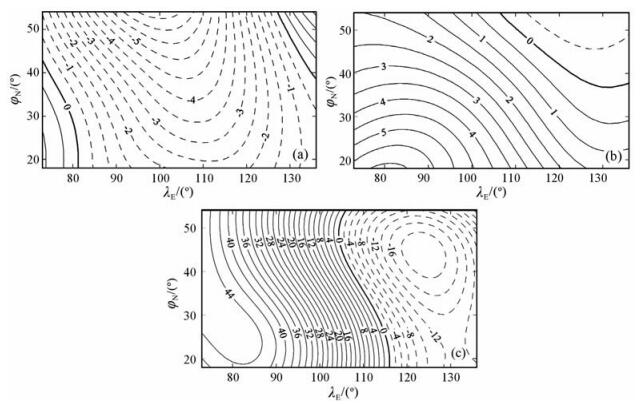
为对比分析各种模型描述的2000.0~2005.0年代中国地区地磁长期变化的异同,给出了根据IGRF2005绘制的2000.0~2005.0年代中国地区地磁长期变化(简称为CIGRF,图 6).对比分析表明,“2000.0~2005.0年代中国地区地磁长期变化泰勒多项式模型”(CTM)和“2000.0~2005.0年代中国地区地磁长期变化曲面样条模型”(CSM)的磁偏角D、磁倾角I和总强度F空间分布(图 3~5)的形态和数值基本一致,而且与CIGRF相近似.这三个模型共同反映了2000.0~2005.0年代中国地区地磁长期变化的基本特征:在中国及周边地区的东北和西南分别存在D的零等变线,在这两条零等变线之间广泛存在着D的负等变线;该负等变线的年变率以蒙古国以北为核心,从北向南其年变率的数值逐渐降低.在华北与东北的交界处存在北西-南东走向的I零等变线,在该线的东北为I的负等变线分布,在该线的西南为I正的等变线分布.在105°E~115°E存在一条近乎南北走向的F零等变线,在该线的东部为F的负等变线分布,在该线的西部为正的等变线分布,而且在中国的东北地区存在着F负等变线的闭合分布.
|
图 6 根据IGRF2005绘制的2000.0~2005.0年代中国地区地磁长期变化 图中实线表示正值, 虚线表示负值.(a)磁偏角D和(b)磁倾角I, 单位:(′)/a, (c)总强度F, 单位:nT/a. Fig. 6 Geomagnetic secular variations inChina for 2000.0~2005.0 established by IGRF2005(CIGEF) In the figure the solid line denotes the positive value and the dashed line denotes the negative value. (a) Declination D, unit:(′)/a, (b) inclination I, unit:(′)/a, (c) total intensity F, unit:nT/a. |
然而,2000.0~2005.0年代中国地区地磁长期变化CTM模型与CIGRF之间存在着较为明显的局部差异.磁偏角D等变线在30°N以南地区近乎东西走向分布的区域(图 3a),比CIGRF描述的同分量等变线的空间分布范围更加宽展(图 6a).在图 3a中,年变率数值为“-2.5(′)/a”的D等变线向南凸出的拐点位于110°E左右,但在图 6a中的该拐点位于115°E左右.在图 4a中,年变率数值为正的磁倾角I等变线簇在85°E左右区域内的空间分布表现为向北凸出,与图 6b中相同区域的分布明显不同.这些差异的存在表明,2000.0~2005.0年代中国地区地磁长期变化的CTM模型比CIGRF更细致、准确地表现了2000.0~2005.0年代中国地区地磁的长期变化.这些差异与中国及周边地区的局部地质构造及构造活动、地下介质的电磁性质、岩石圈结构及其动态变化、地球动力学等因素有关[32, 33, 37].仔细分析可见,2000.0~2005.0年代中国地区地磁长期变化的CTM模型、CSM模型和CIGRF之间存在局部差异,其中CSM模型存在着明显的局部异常分布:在渤海西岸的38°N、117°E,中原地区的35°N、115°E附近存在着D等变线异常分布(图 3b);在37°N、117°E和43°N、117°E附近存在着I等变线异常闭合分布(图 4b);在25°N、95°E~107°E附近存在着总强度F等变线的异常分布(图 5b).CSM模型还存在等变线的局部异常分布:华北到华中地区的D等变线的异常分布,京津冀地区的I等变线的异常分布和川滇交界处的F等变线的异常分布.上述等变线异常分布的空间尺度为数百公里.一般认为,产生地磁长期变化的源位于核幔边界处,到地表的距离为数千公里,不可能在地表产生空间尺度为数百公里的闭合形态的等变线异常.为此,详细分析了各台站地磁日均值分布,结果表明,上述异常主要是由于静海台、郑州台和西昌台地磁日均值的异常分布所引起的.由于曲面样条函数为过点拟合,因此,2000.0~2005.0年代中国地区地磁长期变化CSM模型将上述台站地磁日均值中的异常“忠实”地表现出来了.这说明,虽然地磁曲面样条模型能以相当精细的空间分辨率表现地磁场的局部异常,但对地磁数据的质量亦有相当高的要求.
3种模型的分析比较显示,CTM模型与CSM模型比CIGRF模型更好地描述2000.0~2005.0年代中国地区地磁长期变化,而CSM模型描述得更为细致,因为曲面样条函数为过点拟合,能以相当精细的空间分辨率表现地磁长期变化的局部异常.
上述分析表明,采用地磁日均值比通常采用地磁年均值可以获得地磁长期变化更细致的时间变化.而且含有丰富内外场信息的地磁日均值,可以分析地磁各种成分,进而分析地磁不同的源场,是很有意义的[38].但是,所使用的台站分布不均匀,而且没有地磁重复测量数据可供使用,这对地磁长期变化的分析研究产生不利的影响.
6 结论2000.0~2005.0年代中国地区地磁长期变化的基本特征为,在中国及周边地区的东北和西南分别存在磁偏角的零等变线,在这两条零等变线之间广泛存在着磁偏角的负等变线;该负等变线的年变率以蒙古国以北为核心,从北向南其年变率的数值逐渐降低.在华北与东北的交界处存在北西-南东走向的磁倾角零等变线,在该线的东北为负,该线的西南为正.在105°E~115°E存在一条近乎南北走向的地磁总强度的零等变线,该线的东部为负,该线的西部为正,在中国的东北地区还存在着总强度负等变线的闭合分布.而且,2000.0~2005.0年代中国地区地磁长期变化具有区域特征,即存在地磁长期变化的局部异常,其局部异常与中国及周边地区的局部地质构造及构造活动、地下介质的电磁性质、岩石圈结构及其动态变化、地球动力学等因素有关.
本文应用含有丰富内外源场成分的地磁日均值,得到了中国地区地磁场长期变化的丰富信息.上述3种模型分析研究表明,CTM模型与CSM模型比CIGRF模型更好地描述2000.0~2005.0年代中国地区地磁长期变化,而CSM模型描述得更为细致.在实际应用中,可以根据相关的科学研究与实际项目的要求与需要,适当选用其中的一种模型.
致谢感谢中国地震局地球物理研究所国家地磁台网中心与各地磁台站提供的地磁台站观测数据.感谢两位审者与詹志佳研究员的宝贵意见.
| [1] | 付承义, 陈运泰, 祁贵仲. 地球物理学基础. 北京: 科学出版社, 1985 . Fu C Y, Chen Y T, Qi G Z. Introduction to Geophysics (in Chinese). Beijing: Science Press, 1985 . |
| [2] | Langel R. The main field. In:Jacobs J A ed. Geomagnetism, Vol. 1. London:Academic Press, 1987 |
| [3] | 徐文耀. 地磁学. 北京: 地震出版社, 2003 . Xu W Y. Geomagnetism (in Chinese). Beijing: Seismological Press, 2003 . |
| [4] | IAGA Commission 2, Working Group 4. International Geomagnetic Reference Field 1965.0. J. Geophys. Res. , 1969, 74: 4407-4408. DOI:10.1029/JB074i017p04407 |
| [5] | IAGA Division 1, Working Group 1. International Geomagnetic Reference Field Revision 1985. J. Geomag. Geoelectr. , 1985, 37: 1157-1163. DOI:10.5636/jgg.37.1157 |
| [6] | Barton C E. International Geomagnetic Reference Field:the seventh generation. J. Geomag. Geoelectr. , 1997, 49(1): 123-156. |
| [7] | Mandea M, Macmillan S. International Geomagnetic Reference Field-the eighth generation. Earth Planets Space , 2000, 52(12): 1119-1124. DOI:10.1186/BF03352342 |
| [8] | IAGA Division V, Working Group 8. The 9th Generation International Geomagnetic Reference Field. Geophys. J. Int. , 2003, 155: 1051-1056. DOI:10.1111/gji.2003.155.issue-3 |
| [9] | IAGA Division V, Working Group 8. International Geomagnetic Reference Field 2000. Geophys. J. Int. , 2000, 141: 259-262. DOI:10.1046/j.1365-246x.2000.00121.x |
| [10] | Maus S, Macmillan S, Chernova T, et al. The 10th generation International Geomagnetic Reference Field. Phys. Earth Planet. Inter. , 2005, 151: 320-322. DOI:10.1016/j.pepi.2005.03.006 |
| [11] | Alldredge L. Rectangular harmonic analysis applied to the geomagnetic field. J. Geophys. Res. , 1981, 86(B): 3021-3026. |
| [12] | Alldredge L. Geomagnetic local and regional harmonic analysis. J. Geophys. Res. , 1982, 87(B): 1921-1926. |
| [13] | Maln S R C. On the unpredictability of geomagnetic secular variation. Phys. Earth Planet. Inter. , 1983, 32: 114-131. DOI:10.1016/0031-9201(83)90133-4 |
| [14] | Haines G V, Newitt L R. Canadian geomagnetic reference field 1985. J. Geomag. Geoelectr. , 1986, 38: 895-921. DOI:10.5636/jgg.38.895 |
| [15] | Vassal J. Secular change in the geomagnetic field in west Africa for thirty years:comparison with fourth generation IGRF models. J. Geomag. Geoelectr. , 1987, 39(3): 699-707. |
| [16] | Newitt L R, Haines G V. A Canadian geomagnetic reference field for epoch 1987.5. J. Geomag. Geoelectr. , 1989, 41(2): 249-260. DOI:10.5636/jgg.41.249 |
| [17] | Kote M, Haok V. Modeling European magnetic repeat station and survey data by SCHA in search of time-variation anomalies. Phys. Earth Planet. Inter. , 2000, 122(3-4): 205-220. DOI:10.1016/S0031-9201(00)00194-1 |
| [18] | Burdelnaya I A, Filippov S V, Golovkov V P, et al. Regional orthogonal models of the geomagnetic field changes over the Far East. Earth Planets Space , 1999, 51(4): 287-296. DOI:10.1186/BF03352232 |
| [19] | Ji X, Ushiki M, Shirai A, et al. Modelling of spatial-temporal changes of the geomagnetic field in Japan. Earth Planets Space , 2006, 58(6): 757-763. DOI:10.1186/BF03351979 |
| [20] | Golovkov V P, Bondar T N, Burdelnaya I A. Using satellite magnetic survey data for spatial-temporal modeling of the geomagnetic secular variation. J. Geomag. Geoelectr. , 1997, 49: 207-227. DOI:10.5636/jgg.49.207 |
| [21] | Golovkov V P, Bondar T N, Burdelnaya I A. Spatial-temporal modeling of the geomagnetic field for 1980-2000 period and a candidate IGRF secular-variation model for 2000-2005. Earth Planets Space , 2000, 52(12): 1125-1135. DOI:10.1186/BF03352343 |
| [22] | 徐文耀, 朱岗崑. 我国及邻近地区地磁场的矩谐分析. 地球物理学报 , 1984, 27(6): 511–522. Xu W Y, Tschu K K. A study of the RHA for the geomagnetic field of China and neighbouring region. Chinese J. Geophys. (Acta Geophysica Sinica) (in Chinese) , 1984, 27(6): 511-522. |
| [23] | 朱岗昆, 徐文耀. 我国及邻近地区的嵌套式磁场模型. 地球物理学报 , 1985, 28(2): 133–141. Tschu K K, Xu W Y. A nested geomagnetic model of China and neighbouring region. Chinese J. Geophys (Acta Geophysica Sinica) (in Chinese) , 1985, 28(2): 133-141. |
| [24] | 安振昌. 中国地区地磁场的球冠谐和分析. 地球物理学报 , 1993, 36(6): 753–764. An Z C. Spherical cap harmonic analysis of geomagnetic field for China. Chinese J. Geophys.(Acta Geophysica Sinica) (in Chinese) , 1993, 36(6): 753-764. |
| [25] | 顾左文, 安振昌, 高金田, 等. 京津冀地区地磁场球冠谐分析. 地球物理学报 , 2004, 47(6): 1003–1008. Gu Z W, An Z C, Gao J T, et al. Spherical cap harmonic analysis on the geomagnetic field in Beijing-Tianjin-Hebei region. Chinese J. Geophys. (in Chinese) , 2004, 47(6): 1003-1008. |
| [26] | 高金田, 安振昌, 顾左文, 等. 地磁正常场的选取与地磁异常场的计算. 地球物理学报 , 2005, 48(1): 51–62. Gao J T, An Z C, Gu Z W, et al. Selections of geomagnetic normal field and calculations of geomagnetic anomalous field. Chinese J. Geophys. (in Chinese) , 2005, 48(1): 51-62. |
| [27] | 夏国辉, 郑双良, 吴莉兰, 等. 1980年代中国地磁正常场图及其数学模式. 地球物理学报 , 1988, 31(1): 82–89. Xia G H, Zheng S L, Wu L L, et al. The geomagnetic field chart of China in 1980.0 and the mathematical model. Chinese J. Geophys. (Acta Geophysica Sinica) (in Chinese) , 1988, 31(1): 82-89. |
| [28] | Xu W Y, Xia G H, An Z C, et al. Magnetic survey and China GRF2000. Earth Planets Space , 2003, 55(4): 215-217. DOI:10.1186/BF03351750 |
| [29] | Gu Z, Zhan Z, Gao J, et al. Geomagnetic survey and geomagnetic model research in China. Earth Planets Space , 2006, 58(6): 741-750. DOI:10.1186/BF03351977 |
| [30] | 徐文耀, 魏志刚, 夏国辉. 2000年中国地区地磁场长期变化的区域特征. 地球物理学报 , 2005, 48(3): 551–560. Xu W Y, Wei Z G, Xia G H. Regional features of the secular variations of the geomagnetic field in China for 2000. Chinese J. Geophys. (in Chinese) , 2005, 48(3): 551-560. |
| [31] | 高金田, 安振昌, 顾左文, 等. 用曲面Spline方法表示1900-1936年中国(部分地区)地磁场及其长期变化的分布. 地球物理学报 , 2006, 49(2): 97–107. Gao J T, An Z C, Gu Z W, et al. Distribution of geomagnetic field and its secular variations expressed by the surface spline method in China (a part) for 1900-1936. Chinese J. Geophys. (in Chinese) , 2006, 49(2): 97-107. |
| [32] | Sumitomo N. Geomagnetic secular variation anomalies in relation to the recent crustal movement in the southwestern region of Japan. Bull. Disac. Prev. Res. Inst., Kyoto Univ. , 1981, 30(4-274): 97-130. |
| [33] | Johnston M, Silverman S, Mueller R. Secular variation, crustal contributions and tectonic activity in California, 1976-1984. J. Geophys. Res. , 1985, 90: 8707-8717. DOI:10.1029/JB090iB10p08707 |
| [34] | BurgaudS J, 鲁如曾. 中国地磁图. 徐家汇验磁台地磁丛报 , 1937, 40: 1–74. Burgaud S J, Lu R Z. China geomagnetic chart. Geomagnetic Bulletin of Xujiahui Geomagnetic Observatory (in Chinese) , 1937, 40: 1-74. |
| [35] | 张崇阳, 顾子明.地磁台站概况.见:国家地震局科技监测司编.地震监测与预报方法清理成果汇编--地磁地电分册.北京:地震出版社, 1988 Zhang C Y, Gu Z M. Introduction of geomagnetic observatories. In:Department of Science and Monitoring, China Earthquake Administration ed. The Results of Earthquake Monitoring and Prediction Method-Geomagnetism and Geoelectricity (in Chinese). Beijing:Seismological Press, 1988 |
| [36] | 顾左文, 安振昌, 高金田, 等. 2003.5年中国及邻区地磁场模型的计算与分析. 地震学报 , 2006, 19(2): 145–154. Gu Z W, An Z C, Gao J T, et al. Computation and analysis of the geomagnetic field model in China and its adjacent area for 2003.5. Acta Seismologica Sinica (in Chinese) , 2006, 19(2): 145-154. DOI:10.1007/s11589-002-0145-4 |
| [37] | Gu Z W, Zhan Z J, Gao J T. Seismomagnetic research in Beijing and its adjacent area, China. Physics and Chemistry of the Earth , 2006, 31: 258-267. DOI:10.1016/j.pce.2005.10.002 |
| [38] | 顾左文, 陈斌, 高金田, 等. 应用NOC方法研究中国地区地磁时空变化. 地球物理学报 , 2009, 52(10): 2602–2612. Gu Z W, Chen B, Gao J T, et al. Research of geomagnetic spatial-temporal variations in China by NOC method. Chinese J. Geophys. (in Chinese) , 2009, 52(10): 2602-2612. |
 2010, Vol. 53
2010, Vol. 53