在地震波入射下,沉积谷地显著影响着地震动的空间分布特征并进而影响到地震灾害的程度与分布.因此,沉积谷地对地震波的散射是地球物理学、地震学和地震工程学领域一个重要的研究课题.研究地震波散射问题的理论方法包括数值方法和解析方法.数值方法是求解复杂的实际波动问题强有力的工具,但采用解析手段研究规则沉积谷地的波动对认识问题的物理规律有重要帮助,其得到的精确结果能够用来检验各种数值解的精度,并对实际问题的解决提供一种量级上的估计,而且解析方法在宽频内有独到的优势[1].最常用的解析法是波函数的Fourier-Bessel级数展开法[2~4].
针对沉积谷地对Rayleigh波的散射问题,目前已推导出了单相[5, 6]与多相[7~9]介质条件下二维浅圆形谷地以及单相[10]与多相[11]介质条件下三维半球形谷地对入射Rayleigh波散射问题的解析解.在这些解析解中,通常将谷地中的沉积介质假定为单一沉积[5~7, 10, 11]或两层沉积[8, 9],其中文献[8]研究了谷地中单一饱和土沉积层上覆盖水(假定为无黏性理想流体)的情况,而文献[9]则研究了具有两个饱和土沉积层的谷地对Rayleigh波的散射效应.实际的谷地中通常含有多个沉积层[12~14],为了将上述研究成果拓展到任意多层情况,本文首先尝试利用波函数的Fourier-Bessel级数展开法,在频域内推导出了单相介质条件下含任意多个圆弧状沉积层的谷地对Rayleigh波二维散射问题的解析解,其求解思路可推广到多相介质情况.其次,本文对无穷Fourier-Bessel级数的截断项数、用于计算Rayleigh波自由场的有限Fourier级数的项数、以及用于模拟水平地表的大圆弧的半径对级数解的影响进行了分析,其结果表明,本文给出的解析解能够在一个非常宽的频带范围(η≤30.0)内收敛.最后,利用该解析解,本文在一个较宽的频带范围内探讨了谷地中沉积介质的成层性,包括沉积层的层数以及软弱夹层的刚度和厚度等因素对地面运动的影响.
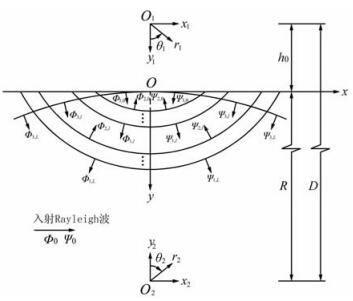
2 模型圆弧状多层沉积谷地的模型如图 1所示,谷地中共有L个沉积层,相邻沉积层之间为圆弧形边界,所有圆弧边界的圆心为O1点,其距离水平地表的高度为h0,圆弧边界的半宽、深度和半径分别记为al、hl和bl(l=1,2,…,L).所有介质(包括半空间介质)均假定为均匀、线弹性和各向同性,其密度、波松比和剪切波速分别记为ρl、νl和βl(l=0,1,2,…,L),相应的介质拉梅常数和纵波波速为
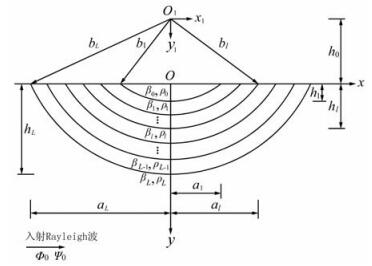
|
图 1 圆弧状多层沉积谷地的模型 Fig. 1 The model of alluvial valley |
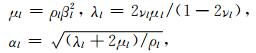
|
(1) |
半空间介质中Rayleigh波的波速记为cR.
入射Rayleigh波的圆频率为ω,在坐标系x-y下,其势函数为
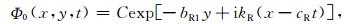
|
(2a) |
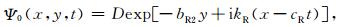
|
(2b) |
其中

|
(3a) |
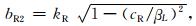
|
(3b) |
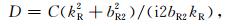
|
(3c) |
其中,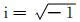
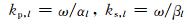
|
(4) |
分别为第l层介质中P波和SV波的圆波数.
稳态情况下,P波的势函数Φ和SV波的势函数Ψ分别满足如下方程
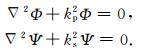
|
(5) |
散射问题的边界条件包括水平地表零应力边界条件
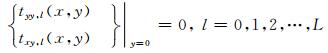
|
(6) |
和第l个圆弧边界处的连续条件(l=1,2,…,L)
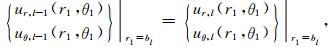
|
(7a) |
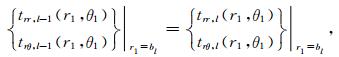
|
(7b) |
其中,tyy,l和txy,l分别表示直角坐标系下第l层介质中的正应力和剪应力,ur,l和uθ,l分别表示极坐标系下第l层介质中的法向位移和切向位移,trr,l和trθ,l分别表示极坐标系下第l层介质中的法向正应力和切向剪应力.
3 波的势函数为了在极坐标系下获得散射问题的解,本文依然采用Todorovska和Lee[3]对水平地表的处理方法,即用一个半径非常大的圆弧近似模拟水平地表,其圆心为O2,半径为R,如图 2所示.当半径R的值很大时,图 2所示模型得出的解将收敛于真实解,这将在下文中讨论.在图 2所示的极坐标系r2-θ2下,零应力条件(6)式变换为
|
图 2 波的散射图 Fig. 2 The scattering of waves |
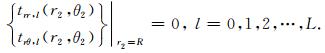
|
半空间介质中存在自由场波和散射波.自由场波的势函数由(2)式给出,在坐标系r1-θ1下可写为(考虑稳态情况,本文所有波函数的时间因子exp(-iωt)均被略去):
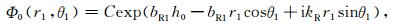
|
(8a) |
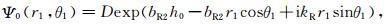
|
(8b) |
如图 2所示,半空间中由于沉积谷地的存在而产生的散射波包括圆弧L处由O1点向外辐射的柱面行波Φ1,L和Ψ1,L、以及模拟水平地表的大圆弧内的柱面驻波Φ3,L和Ψ3,L,在极坐标系r1-θ1和r2-θ2下,它们分别具有如下Fourier-Bessel级数形式:
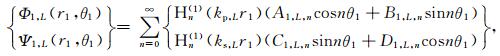
|
(9) |

|
(10) |
其中,函数Hn(1)(x)和Jn(x)分别表示第一类Hankel函数(即第三类Bessel函数)和第一类Bessel函数,A1,L,n至D3,L,m为未知的待定系数.利用如下内域型Graf加法公式[15]
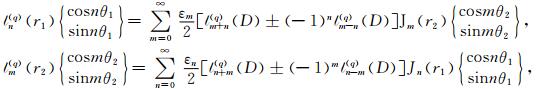
|
(11) |
式(9)和式(10)给出的散射波的势函数在极坐标系r2-θ2和r1-θ1下可分别表示为
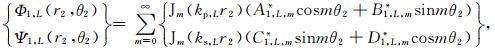
|
(12) |
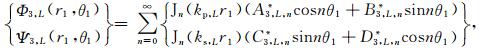
|
(13) |
其中
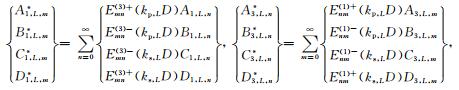
|
(14) |
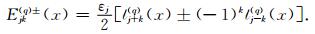
|
(15) |
在(11)式和(15)式中,当m=0时εm=1,当m>0时εm=2;另外,当q=1时,ln(q)(x)表示函数Jn(x),当q=3时,ln(q)(x)表示函数Hn(1)(x).在(14)式中,D表示圆心O1和O2之间的距离,如图 2所示.
3.2 沉积介质中散射波的势函数如图 2所示,在第l层(l=0,1,…,L-1)沉积介质中存在三种散射波:小圆弧l外的柱面行波Φ1,L和Ψ1,L、小圆弧l+1内的柱面驻波Φ2,l和Ψ2,l、以及大圆弧内的柱面驻波Φ3,L和Ψ3,l.当l=0时,上述柱面行波不存在,Φ1,0=Ψ1,0=0,即在最表层的沉积介质中只有两种柱面驻波,如图 2所示.在极坐标系r1-θ1和r2-θ2下,上述散射波的势函数具有如下表达式
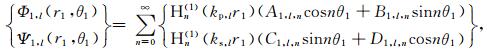
|
(16) |
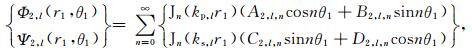
|
(17) |
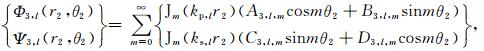
|
(18) |

|
(19) |

|
(20) |
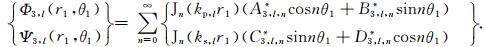
|
(21) |
根据Graf加法公式(11),上述不同坐标系下散射波的待定系数之间存在如下关系
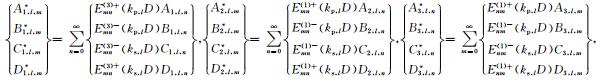
|
(22) |
当l=0时,
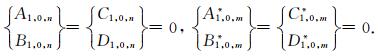
|
(23) |
自由场波和散射波势函数的Fourier-Bessel级数表达式给定之后,相应的位移与应力表达式可根据如下公式推导得出
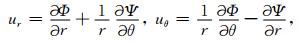
|
(24) |
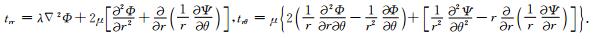
|
(25) |
在极坐标系r1-θ1下,与势函数对Φ1,L和Ψ1,L、Φ2,l和Ψ2,l、以及Φ3,L和Ψ3,l对应的位移和应力可表示为
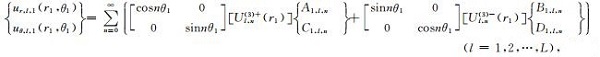
|
(26a) |

|
(26b) |
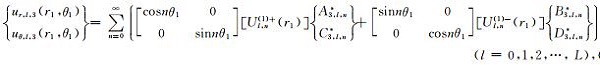
|
(26c) |
以及
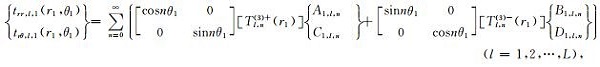
|
(27a) |
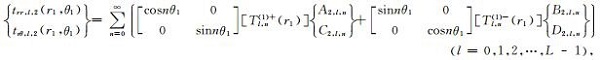
|
(27b) |
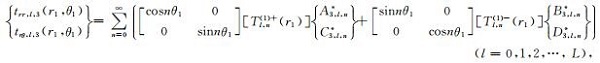
|
(27c) |
其中

|
(28) |
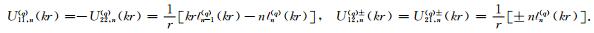
|
(29) |
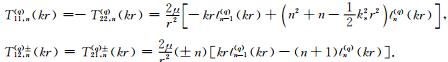
|
(30) |
此外,与(8)式给出的自由场波的势函数对应的位移场与应力场在圆弧边界r1=bL上可近似表示为如下有限Fourier级数:
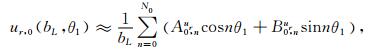
|
(31a) |
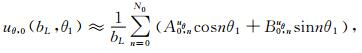
|
(31b) |
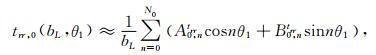
|
(31c) |
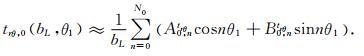
|
(31d) |
系数A0,nur至B0,ntrθ可利用有限Fourier变换确定,其具体计算参见文献[5],本文此处不再赘述.式(31)中,N0为有限Fourier级数的项数,其值越大,计算精度越高,下文中将讨论其取值对解的影响.
极坐标系r2-θ2主要是为了引入地表零应力边界条件,在该坐标系下应力可表示为

|
(32a) |
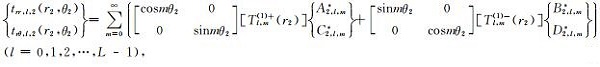
|
(32b) |
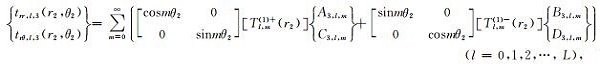
|
(32c) |
自由场波函数对地表应力贡献为零,因此在模拟地表的大圆弧边界处,将(32)式代入零应力条件(6)式中,并利用(14)式和(22)式可得到如下关系
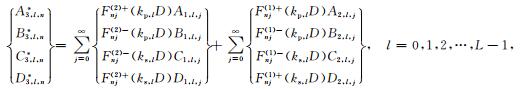
|
(33a) |

|
(33b) |
其中

|
(34) |
首先,针对最表层的沉积介质,即当l=0时,由(23)式可得
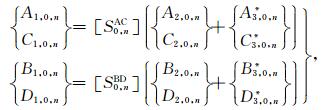
|
(35) |
其中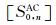
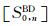
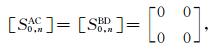
|
(36) |
其次,依次针对第l个圆弧边界(l=1,2,…,L-1),将(26)式与(27)式分别代入连续条件(7)式中可得如下关系
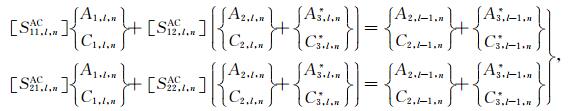
|
(37) |
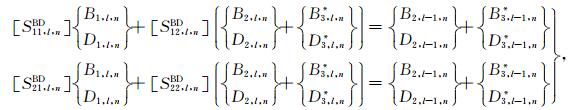
|
(38) |
其中
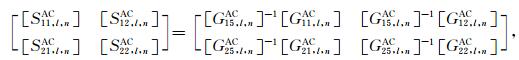
|
(39a) |
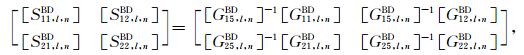
|
(39b) |
矩阵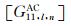
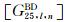
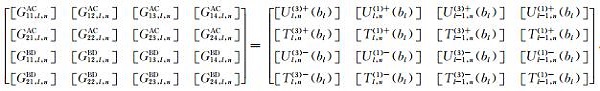
|
(40a) |
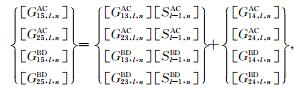
|
(40b) |
分别合并(37)式与(38)式可得到第l层沉积介质中散射波待定系数之间的关系
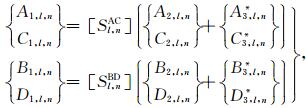
|
(41) |
其中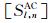
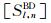
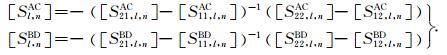
|
(42) |
自(36)式给定的最表层沉积介质(l=0)中散射波待定系数之间的关系矩阵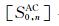

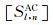
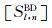
最后,针对第L个圆弧边界,将(26)、(27)和(31)式代入连续条件(7)式中可得
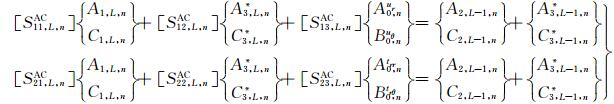
|
(43) |

|
(44) |
其中
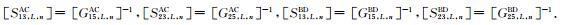
|
(45) |
其他矩阵可利用(39)式与(40)式计算.分别合并(43)、(44)两式可得
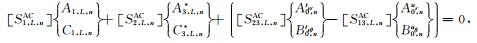
|
(46) |
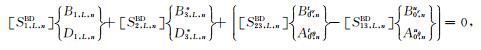
|
(47) |
其中
|
(48) |
首先针对半空间介质,即l=L,将(33b)式分别代入(46)和(47)式中可得如下关于系数对A1,L,j和C1,L,j以及系数对B1,L,j和D1,L,j的方程组:

|
(49) |
其中
|
(50a) |
|
(50b) |
|
(50c) |
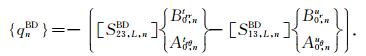
|
(50d) |
在上述方程中,如果n=j,则δnj=1,否则δnj=0;[S]ij表示矩阵[S]的第i行、第j列元素.
将无穷级数自有限项截断并求解方程组(49)即可确定待定系数A1,L,n、C1,L,n、B1,L,n和D1,L,n,之后利用(33b)式可进一步确定系数A3,L,n*、C3,L,n*、B3,L,n*和D3,L,n*.因此,半空间介质中散射波的待定系数均已确定.
其次,依次针对第l层沉积介质,l=L-1,L-2,…,0,首先合并(43)、(44)和(41)式(针对l=L-1)或合并(37)、(38)和(41)式(针对l=L-2,L-3,…,0),可以确定各层介质中柱面行波的待定系数A1,L,n、C1,l,n、B1,l,n和D1,l,n:
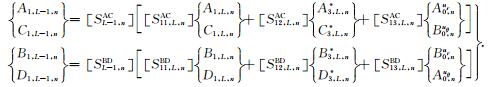
|
(51a) |
或
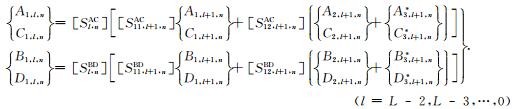
|
(51b) |
之后,将(33a)式代入(41)式可得如下关于待定系数对A2,l,j和C2,l,j以及系数对B2,l,j和D2,l,j的方程组
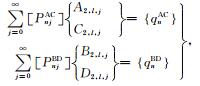
|
(52) |
其中
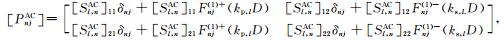
|
(53a) |

|
(53b) |

|
(53c) |
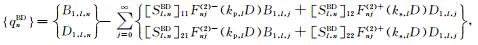
|
(53d) |
求解方程组(52)可确定待定系数A2,l,j、C2,l,j、B2,l,j和D2,l,j,之后利用(33a)式可确定系数A3,l,n*、C3,l,n*、B3,l,n*和D3,l,n*.因此,所有沉积介质中散射波的待定系数均已按照上述顺序(l=L-1,L-2,…,1,0)以递推的方式确定.最后,利用(26)和(27)式,可确定整个位移场和应力场,从而确定了整个散射问题的解.
6 结果分析定义如下参数以描述入射Rayleigh波的频率
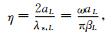
|
(54) |
其物理意义为谷地总宽度2aL与半空间S波波长λs,L之间的比值,它间接地描述了入射Rayleigh波的频率ω:η越大,入射波波长越小,频率越高.
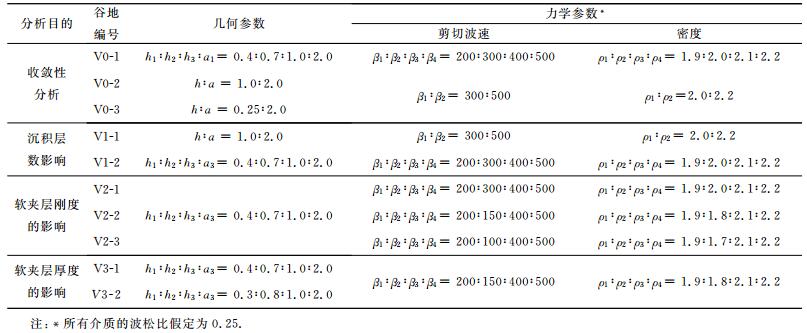
表 1给出了本文的结果分析工作所涉及到的所有谷地的几何参数和力学参数.谷地的几何形状与力学性质均以参数比值的方式予以确定.
|
|
表 1 本文研究用到的不同谷地的几何参数与力学参数 Table 1 Geometrical and mechanical parameters of different valleys used in this study |
在解析解的求解过程中,需要将无穷Fourier-Bessel级数截断,即将(49)和(52)式给出的无穷维线性方程组截断并求解,进而获得整个散射问题的解.级数解的收敛性可按如下原则判断:针对任一空间点(x,y),首先计算自有限项N截断所得的位移u(N;x,y),然后计算自N+1项截断所得的位移u(N+1;x,y),计算二者之间的误差
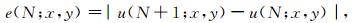
|
(55) |
若对于某一截断项数Nc,当N≥Nc时,
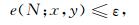
|
(56) |
则项数Nc即认为是级数的收敛项数.式(55)中,u表示x方向位移ux或y方向位移uy;式(56)中,ε为控制计算精度的参数,本文取ε=10-6.
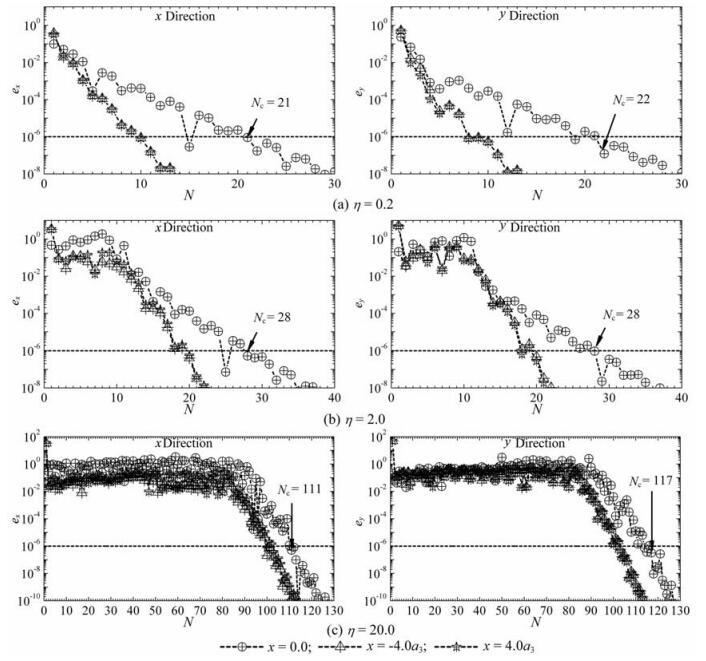
表 1中的谷地V0-1为三层沉积谷地,考虑该谷地3个地表点位移的收敛性,在坐标系x-y下,这3个点的坐标分别为(0,0)、(4a3,0)、(-4a3,0).在入射Rayleigh波频率η=0.2、2.0和20.0的情况下,由(55)式计算出的这三个点的误差ex,ey与截断项数N之间的关系如图 3所示.可以看出,针对任一空间点,随着截断项数的增加,相邻截断项数之间的误差逐渐减小,当截断项数超过某一数值时,该误差将低于10-6,意味着级数解收敛.入射波频率越高,级数收敛所需项数越多,例如针对谷地地表中心点,即点(0,0),入射波频率η=0.2、2.0和20.0所需的收敛项数依次为22、28和117.此外,不同空间点位移的收敛所需截断项数也有所不同,如图 3所示,谷地中心点(x=0)位移的收敛项数高于谷地之外地表点(x=±4.0a3)位移的收敛项数.
|
图 3 级数解随截断项数的收敛性 Fig. 3 The convergence of series solution with the truncation number |
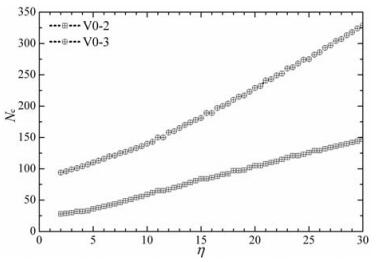
除入射波频率外,谷地几何形状也影响解的收敛项数.考虑表 1给出的两个单一沉积谷地V0-2和V0-3,它们的宽度与力学参数相同,但相比谷地V0-2(h:a=1.0:2.0),谷地V0-3(h:a=0.25:2.0)更浅.这两个谷地地表中心点位移的收敛项数与入射波频率之间的关系如图 4所示.从中可以看出,谷地越浅、入射波频率越高,级数解收敛所需项数越多.而且本文给出的解在η=30.0的极高频情况下依然能够收敛.
|
图 4 谷地几何形状对级数解收敛性的影响 Fig. 4 The influence of valley geometry on the convergence of series solution |
下面分析一下Rayleigh波自由场有限Fourier展开的项数,即(31)式中的项数N0,对解的影响.在现有的针对Rayleigh波或入射角大于临界角的SV波散射问题的解析解的研究工作中[5, 6],通常根据散射波函数的Fourier-Bessel级数的截断项数,即式(55)中的项数N,确定自由场有限Fourier展开的项数N0.在本文的研究过程中发现,这一做法会影响高频波入射下解的收敛性.因此,本文对这一求解过程进行了改进,即在对散射波函数的Fourier-Bessel级数截断之前,首先用一个非常大的项数N0对Rayleigh波自由场的Fourier级数展开进行截断,项数N0独立于并且可以远大于项数N.采用这种方式处理后,本文给出的解即使在频率很高(例如η=20.0)的情况下依然具有很好的收敛性,如图 3c所示,其中自由场有限Fourier级数的项数N0=4096.图 5说明了项数N0的选取对解的影响,其中谷地为表 1给出的单层谷地V0-2,入射波的频率η=2.0.图 5给出的是地表x和y方向位移的幅值和相位的空间变化曲线,N0的值依次取为64、128、4096、16384.从中可以看出,N0=4096的计算结果与N0=16384的计算结果已经非常接近,因此实际计算可取N0=4096.

|
图 5 自由场有限Fourier级数的项数N0对解的影响 Fig. 5 Influence of the number of terms of free-field finite Fourier series on the solution |
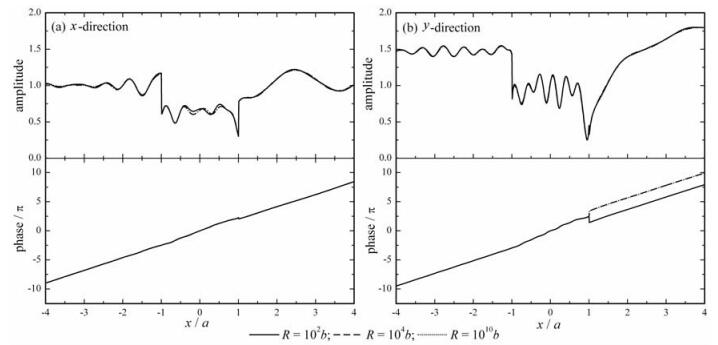
在本文解析解的推导过程中,需用一半径非常大的圆弧近似模拟水平地表,如图 2所示.当大圆弧的半径R非常大时,所得解将趋近于真实解.图 6给出了大圆弧半径的选取对解的影响,其中谷地依然为V0-2,入射波频率η=2.0.可以看出,大圆弧半径R=104b的计算结果与R=1010b的计算结果非常接近,因此实际计算可取R=104b,其中b为谷地最外层圆弧边界的半径.
|
图 6 模拟水平地表的大圆弧的半径只对解的影响 Fig. 6 Influence of the radius of the big arc simulating the levfl surface on the solution |
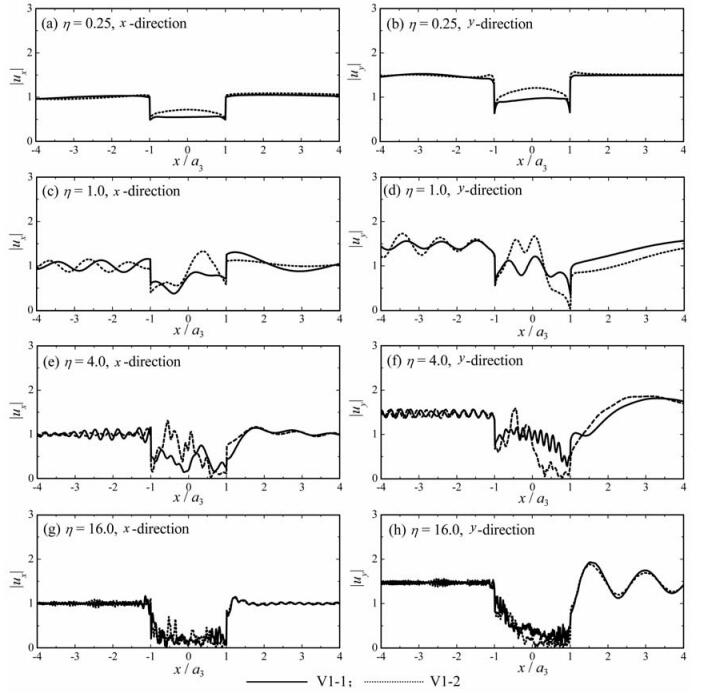
首先分析谷地沉积层数的影响.考虑表 1给出的谷地V1-1和V1-2,它们的几何形状相同,谷地V1-2含有三个沉积层,而谷地V1-1为单层沉积,且谷地V1-1沉积介质的力学参数为谷地V1-2中三种沉积介质相应参数的均值,如表 1所示.图 7给出了两个谷地地表位移幅值之间的比较,入射波的频率η=0.25、1.0、4.0和16.0.从中可以看出,无论是在低频波还是在高频波入射下,在谷地地表中心地带(-1<x/a3<1),两个谷地地表位移幅值具有明显的差别,谷地沉积层数显著影响着地面运动的强度及其分布.而且,即使在较低频Rayleigh波入射的情况下(η=0.25和1.0),将谷地中多层沉积介质简化为单一介质也将引起较大误差.
|
图 7 谷地沉积层数对地面运动的影响 Fig. 7 Influence of the number of valley layers on the ground motion |
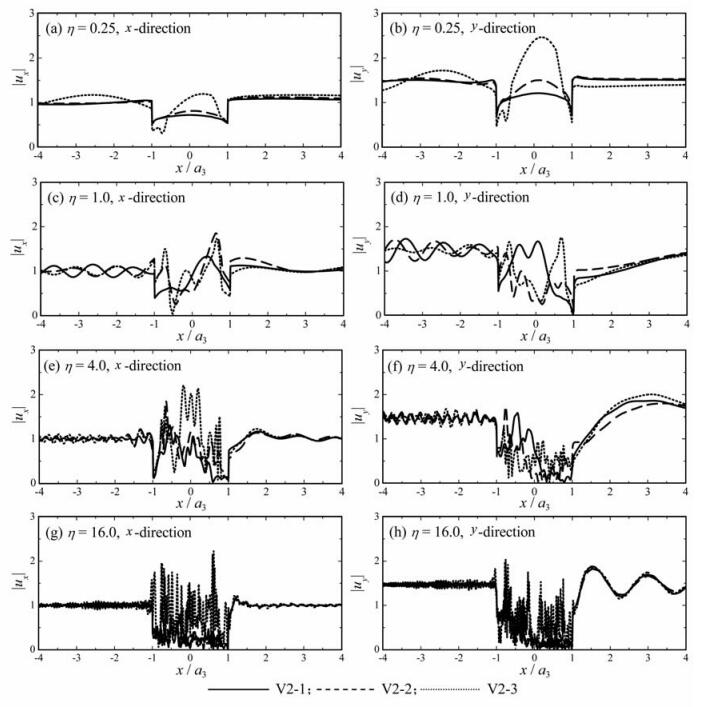
图 8给出了谷地中软弱夹层及其刚度的变化对地面运动的影响.其中谷地模型为表 1中的谷地V2-1、V2-2和V2-3,这三个谷地均为三层沉积,除第二个沉积层的力学参数外,它们其他的几何与力学性质完全一致.V2-1为正常沉积谷地,V2-2和V2-3为非正常沉积,第二个沉积层为软夹层,且V2-3软夹层的刚度低于V2-2软夹层的刚度,如表 1所示.如图 8所示,在低频波(η=0.25)入射下,地表位移幅值的变化有较为明显的规律:在地表中心地带,具有软夹层的谷地位移幅值较大,且软夹层刚度越小,地表位移幅值越大.在较高频波(η=1.0、4.0和16.0)入射下,地表位移变化复杂,较为明显的规律是,在地表软夹层出露部位,即0.6<|x/a3|<0.8,含有软夹层的谷地V2-2和V2-3的地表位移幅值明显高于正常沉积谷地V2-1的,且大部分情况下谷地V2-3的位移幅值高于V2-2的.这说明了谷地中的软夹层会吸收较多的散射波能量,从而造成其地表出露部位较高的地面运动幅值.
|
图 8 谷地软弱夹层的存在及其刚度对地面运动的影响 Fig. 8 Influence of the existence of soft interlayer in the valley and its stiffness on the ground motion |
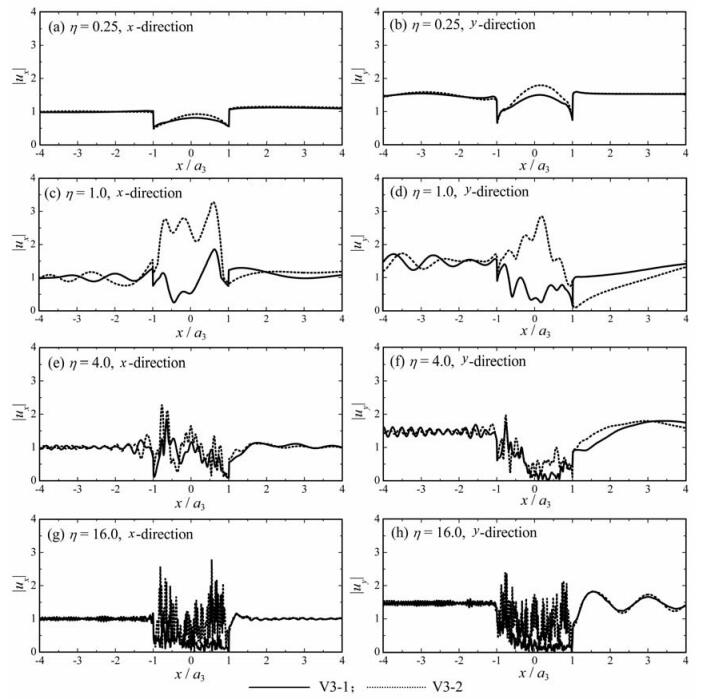
图 9给出了谷地中软夹层的厚度对地面运动的影响.谷地模型为表 1中的谷地V3-1和V3-2,均为三层非正常沉积,第二层为软夹层.这两个谷地力学参数完全相同,与谷地V3-1软夹层的厚度(h2 -h1=0.15a3)相比,谷地V3-2软夹层的厚度(0.25a3)更大.从图 9中可以看出,针对所有入射波频率η=0.25、1.0、4.0和16.0,在谷地地表中心地带(|x/a3 |<1.0),V3-2的位移幅值均高于V3-1,这种现象在η=1.0和16.0的情况下最为显著.这说明非正常沉积谷地中软夹层厚度的增加对谷地地表中心地带地面运动的强度具有放大效应.
|
图 9 谷地软弱夹层的厚度对地面运动的影响 Fig. 9 Influence of the thickness of soft interlayer in the valley on the ground motion |
本文求解并研究了含任意多个圆弧状沉积层的谷地在Rayleigh波入射下的动力响应.首先,通过将未知散射波的势函数在柱坐标系下展开成Fourier-Bessel级数的形式、并利用边界条件确定其待定系数,推导了给定二维散射问题的解析解.其次,分析了无穷Fourier-Bessel级数的截断项数、Rayleigh波自由场的有限Fourier展开的项数、以及用于模拟水平地表的大圆弧的半径对级数解的影响.最后,利用该解在宽频带范围内分析了谷地介质的成层性对稳态地面运动的影响,其结果表明,在Rayleigh波入射下,谷地沉积层的层数、谷地中软弱夹层的刚度和厚度等因素显著影响着谷地地面运动的强度及其分布特征.
| [1] | 袁晓铭, 李雨润, 孙锐. 圆弧状沉积盆地与软土单覆盖层出平面地表运动对比. 地震工程与工程振动 , 2002, 22(4): 16–21. Yuan X M, Li Y R, Sun R. Comparison of out-of-plane surface ground motion between a circular-arc alluvial valley and a single overburden soft layer. Earthquake Engineering and Engineering Vibration (in Chinese) , 2002, 22(4): 16-21. |
| [2] | Trifunac M D. Surface motion of a semi-cylindrical alluvial valley for incident plane SH waves. Bull. Seism. Soc. Am. , 1971, 61(6): 1755-1770. |
| [3] | Todorovska M I, Lee V W. Surface motion of shallow circular alluvial valleys for incident plane SH wave-analytical solution. Soil Dyn. Earthq. Engrg. , 1991, 10(4): 192-200. DOI:10.1016/0267-7261(91)90033-V |
| [4] | Yuan X M, Liao Z P. Scattering of plane SH waves by a cylindrical alluvial valley of circular-arc cross-section. Earthq. Engrg. Struct. Dyn. , 1995, 24: 1303-1313. DOI:10.1002/(ISSN)1096-9845 |
| [5] | Todorovska M I, Lee V W. A note on response of shallow circular valleys to Rayleigh waves:analytical approach. Earthquake Engineering and Engineering Vibration , 1990, 10(1): 21-34. |
| [6] | 梁建文, 张秋红, 李方杰. 浅圆沉积谷地对瑞雷波的散射-高频解. 地震学报 , 2006, 28(2): 176–182. Liang J W, Zhang Q H, Li F J. Scattering of Rayleigh waves by a shallow ciruclar alluvial valley:high-frequency solution. Acta Seismologica Sinica (in Chinese) , 2006, 28(2): 176-182. |
| [7] | 王磊, 赵成刚. 饱和土沉积谷场地对平面Rayleigh波的散射. 岩土工程学报 , 2007, 29(2): 204–211. Wang L, Zhao C G. Scattering of plane Rayleigh waves in alluvial valleys with saturated soil deposits. Chinese J. Geotechnical Engineering (in Chinese) , 2007, 29(2): 204-211. |
| [8] | 赵成刚, 王磊, 李伟华. 具有饱和土沉积层的充水河谷对平面瑞雷波的散射. 地球物理学报 , 2008, 51(5): 1567–1573. Zhao C G, Wang L, Li W H. Scattering of plane Rayleigh waves by circular-arc alluvial valleys with saturated deposites and water layer. Chinese J. Geophys. (in Chinese) , 2008, 51(5): 1567-1573. |
| [9] | 赵成刚, 王磊, 高福平. 圆弧形沉积场地对平面瑞利波散射的解析分析. 力学学报 , 2007, 39(3): 365–373. Zhao C G, Wang L, Gao F P. Scattering of plane Rayleigh waves by a ciruclar-arc alluvial valley:an analytical solution. Chinese Journal of Theoretical and Applied Mechanics (in Chinese) , 2007, 39(3): 365-373. |
| [10] | 韩铮, 赵成刚. 半球形沉积谷场地对入射平面Rayleigh波的三维散射解析解. 岩土力学 , 2007, 28(12): 2607–2613. Han Z, Zhao C G. Analytical solution of three-dimensional scattering and diffraction of plane Rayleigh-waves by a hemispherical alluvial valley. Rock and Soil Mechanics (in Chinese) , 2007, 28(12): 2607-2613. |
| [11] | 赵成刚, 韩铮. 半球形饱和土沉积谷场地对入射平面Rayleigh波的三维散射问题的解析解. 地球物理学报 , 2007, 50(3): 905–914. Zhao C G, Han Z. Three-dimensional scattering and diffraction of plane Rayleigh-waves by a hemispherical alluvial valley with saturated soil deposit. Chinese J. Geophys. (in Chinese) , 2007, 50(3): 905-914. |
| [12] | Semblat F, Kham M, Parara E, et al. Seismic wave amplification:Basin geometry vs soil layering. Soil Dyn. Earthq. Engrg. , 2005, 25: 529-538. DOI:10.1016/j.soildyn.2004.11.003 |
| [13] | Moeen-Vaziri N, Trifunac M D. Scattering and diffraction of plane SH waves by two-dimensional inhomogeneities. Soil Dyn. Earthq. Engrg. , 1988, 7(4): 179-188. DOI:10.1016/S0267-7261(88)80002-2 |
| [14] | Moeen-Vaziri N, Trifunac M D. Scattering and diffraction of plane P and SV waves by two-dimensional inhomogeneities. Soil Dyn. Earthq. Engrg. , 1988, 7(4): 189-200. DOI:10.1016/S0267-7261(88)80003-4 |
| [15] | Abramowitz M, Stegun I A. Handbook of Mathematical Functions, with Formulas, Graphs, and Mathematical Tables. New York: Dover Publication, 1972 . |
 2010, Vol. 53
2010, Vol. 53