2. 清华大学数学科学系, 北京 100084;
3. 中国人民解放军驻航天科工集团二院军事代表室, 北京 100854;
4. 吉林大学通信工程学院, 长春 130012;
5. 吉林大学地球探测科学与技术学院, 长春 130026
2. Department of Mathematical Sciences, Tsinghua University, Beijing 100084, China;
3. Military Representative Office of PLA in Second Research Institute of CASIC, Beijing 100854, China;
4. College of Communication and Engineering, Jilin University, Changchun 130012, China;
5. College of Geo-exploration Science and Technology, Jilin University, Changchun 130026, China
在地震勘探工程中, 压制干扰、提高信噪比是一项贯穿始终的关键任务, 而提高信噪比的一个突出环节是消减低信噪比资料中的随机噪声.地震资料的去噪方法已有很多, 如能很好地提高水平同相轴信噪比的奇异值分解方法[1], 对较弱高斯噪声有很好压制作用的维纳滤波[2], 适宜于去除脉冲噪声的中值滤波方法[3], 比小波变换更适合于地震数据分析和处理的高阶seislet变换[4]以及可适用于非均匀、各向异性弹性介质中资料处理方法等[5, 6].上述不同方法具有不同的原理、应用条件和局限性.
支持向量机[7] (Support Vector Machine: SVM)方法是近年来机器学习领域的一项重大研究成果, 在分类、回归、预测和诊断等方面已经得到了较为广泛的应用, 其中用于函数回归的SVM常被称为支持向量回归(Support Vector Regression: SVR).在信号处理领域, 一些学者利用SVM对受噪声污染的信号或图像进行了去噪研究, Li[8]将含噪图像划分成3×3窗口, 以窗口内像素值作为输入矢量, 以无噪图像对应窗口的中心值作为目标值进行训练, 仅使用少数图像训练, 在不同于训练图像的其他图像上进行测试, 也取得了较好的效果, 但当测试图像与训练图像模型相差较远时去噪效果较差; Wu等[9]将图像所开窗口内像素的下标作为训练输入, 以中心像素值作为目标进行回归, 根据图像局部特征对标准最小二乘支持向量回归(LeastSquares SVR: LS-SVR)的拉格朗日乘子加权, 提出利用局部自适应LS-SVM去除图像噪声, 由于该方法逐像素点开窗计算, 运算效率很低; 邓小英等[10]提出更适合于地震勘探信号的Ricker子波支持向量回归方法逐道处理地震记录, 去噪效果优于自适应维纳滤波和小波变换方法; Cheng等[11]在小波变换域应用SVM以提高SVM的去噪性能等.一直以来, SVM几乎总是作为机器学习方法在统计学习理论基础上被研究和发展, 具体应用到信号滤波领域中, 尚未有人系统地讨论过SVM滤波器的性能及其影响因素.本文从信号与系统的角度研究LS-SVM滤波器的性质, 研究不同参数对滤波器性能的影响, 并通过去除合成地震记录中随机噪声的仿真实验来验证LS-SVM滤波器的有效性.
2 最小二乘支持向量回归对给定的训练样本集{ui, vi}i=1l, 其中ui∈RN为输入集, vi∈R为对应的目标输出集, l为训练样本数.为了解决实际中普遍存在的非线性回归问题, LS-SVR方法首先利用一非线性映射φ(u): RN→ RNh将数据集从原输入空间映射到某一特征空间, 使输入空间中的非线性回归问题变成高维特征空间中的线性回归问题.设回归函数为:

|
(1) |
其中ω·φ(u)表示权矢量ω ∈RNh与φ(u)之间的内积, b∈R为偏差项.LS-SVR的约束优化问题[9]为:
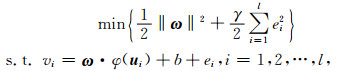
|
(2) |
这里γ是正则化参数, ei(i=1, 2, …, l)∈R是误差变量.
采用拉格朗日乘子法求解该约束优化问题, 构造下面的拉格朗日方程:
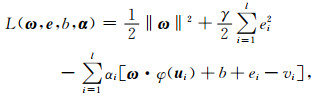
|
(3) |
其中拉格朗日乘子αi(i=1, 2, …, l)∈R.由优化条件有
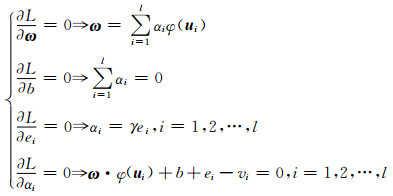
|
(4) |
消掉ω和ei可得到下面的线性方程组
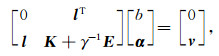
|
(5) |
其中l=[1, 1, …, 1]T, α=[α1, α2, …, αl]T, v=[v1, v2, …, vl]T, E是单位阵, K是核矩阵且其元素Ki, j=φ(ui)·φ(uj).由Mercer理论[12], 可用满足Mercer条件的核函数代替特征空间的内积, 即k(ui, uj)=φ(ui)·φ(uj), 从而大大地简化了核矩阵的计算.令A=K+γ-1E, 由方程组(5)可得

|
(6) |
从而得到回归函数
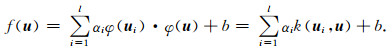
|
(7) |
把LS-SVR应用于信号滤波时可将之看作为一个滤波系统, 其示意如图 1所示.设系统的输入为x(n), n=1, 2, …, l, 若所有待滤波信号均参与训练, 则x(n)即为前述第2节中的vi, 而第2节中的ui(i=1, 2, …, l)被隐含地表示为滤波系统中的离散时间, 即un时刻输入信号的离散采样值为x(n), 系统的输出为y(n), n=1, 2, …, l.

|
图 1 LS-SVR滤波系统示意图 Fig. 1 LS-SVR filtering system |
若将输入信号和输出信号均用列向量表示, 即x=[x(1), x(2), …, x(l)]T, y=[y(1), y(2), …, y(l)]T, 则根据第2节中的推导可得(其中与第2节中相同的符号表示相同的含义):
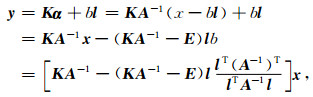
|
(8) |
令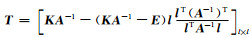
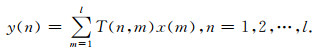
|
(9) |
分析滤波矩阵T, 由于A=K+γ-1E, 所以核矩阵K在其中起着关键的作用, 其元素Ki, j=k(ui, uj).当核函数取定后, 核矩阵K的值仅与信号的采样时刻有关.更进一步地, 对于平移不变核[13](此时k(ui, uj)=k(ui-uj), 如Ricker子波核[10], RBF核等)有更好的特性, 即核矩阵K仅与任意两个信号采样点的时间间隔有关.本文仅讨论这类具有平移不变性的核, 所以对于具有固定采样率和长度的离散时间输入信号, 滤波矩阵T是一个确定的矩阵.
当输入为x1(n)时, 输出为
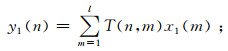
|
当输入为x2(n)时, 输出为
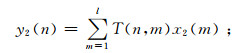
|
则当输入为x(n)=ax1(n)+bx2(n)时(a, b为任意常数), 输出

|
由此可知此滤波系统满足可加性和比例性, 所以LS-SVR滤波系统是一个线性系统.
3.2 时不变性
设输入延迟n0个单位采样间隔, 即输入序列由原来的x=[x(1), x(2), …, x(l)]T变为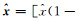
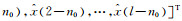
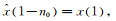
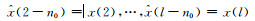
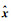
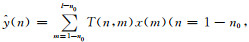
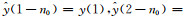
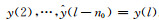
由上可见, 使用平移不变类核的LS-SVR滤波系统是一个线性时不变系统.
3.3 频率响应我们已经证明了平移不变类核LS-SVR滤波系统是一个线性时不变系统, 则该系统可用它的单位冲激响应h(n)来表征, 进而通过傅立叶变换得到系统的频率响应H(ω).由式(9)知, 平移不变类核LS-SVR滤波器的单位冲激响应
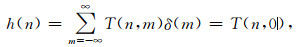
|
其中δ(m)为单位冲激函数.理论上滤波矩阵T的规模应为无穷大, h(n)是无限长的, 实际中我们只能截取有限长度.我们知道支持向量机的泛化性能与选用的核函数以及训练参数的选择密切相关, 参数的不合理选择可能使支持向量机的优越性完全丧失, 因此参数选择是十分重要的, 但就目前来说尚未有较满意的一致看法[14].LS-SVR滤波器的频率响应特性会因选择不同的核函数和不同的参数而不同.对于Ricker子波核
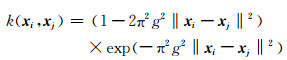
|
(其中g为核参数)和RBF核
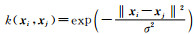
|
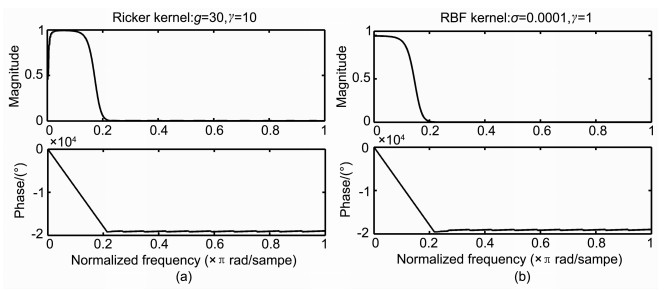
图 2 LS-SVR滤波系统的频率响应(滤波器长度为1000) (a) Ricker子波核;(b) RBF核 Fig. 2 Frequency response of LS-SVR filtering system (length of filter is 1000) (a) Ricker wavelet kernel; (b) RBFkernel. |
(1) 滤波器长度的影响
固定Ricker子波核的核参数g=30以及正则化参数γ=10, 改变滤波器长度以考察其对滤波器性能的影响.图 3给出了滤波器长度分别为3000, 2000, 1000, 500和200点时滤波器的振幅谱.从图 3及其低频部分的放大图可见, 不同长度的Ricker子波核LS-SVR滤波器均呈现带通性质, 但均保留直流分量, 且通带的下降沿基本一致, 主要的区别在于对低频分量的抑制能力上.滤波器长度越长对低频分量压制得越强, 通带部分的上升沿越陡峭, 因此从带通性质来说, 滤波器长度越长越好, 这样能有效地压制低频分量.
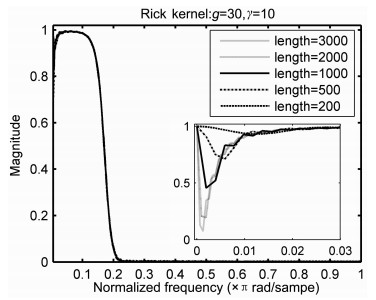
|
图 3 不同长度的LS-SVR滤波器的频率响应(里面的小图为低频部分的放大,下同) Fig. 3 Frequency responses of LS-SVR filters with different lengths |
(2) 核参数的影响
固定滤波器的长度为1000以及正则化参数γ=10, 通过改变Ricker子波核的核参数g以考察核参数对滤波器性能的影响.图 4给出了核参数分别为80, 50, 30, 20和10时滤波器的振幅谱.从图 4及其低频部分的放大图可见, 不同核参数的Ricker子波核LS-SVR滤波器均呈现带通性质, 主要区别在于通带中心频率和通带带宽不同.核参数值增大, 通带的中心频率向高频移动, 而且通带带宽逐渐增宽; 相反, 核参数值减小, 通带的中心频率向低频移动, 而且通带带宽越来越窄.对于一个确定的核参数(其他条件不变), 其频率响应的中心频率和通带带宽也是确定的, 因而可通过调整核参数使Ricker子波核LS-SVR滤波器能筛选出不同频带的信号.
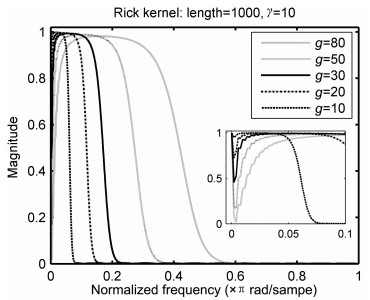
|
图 4 不同核参数的LS-SVR滤波器的频率响应 Fig. 4 Frequency responses of LS-SVR filters with different kernel parameters |
(3) 正则化参数的影响
固定Ricker子波核的核参数g=30以及滤波器长度为1000, 通过改变正则化参数γ以考察其对滤波器性能的影响.图 5给出了正则化参数γ分别为100, 10, 1, 0.1和0.01时滤波器的振幅谱.从图 5及其低频部分的放大图可见, 不同正则化参数的Ricker子波核LS-SVR滤波器均呈现带通性质, 但均保留直流分量, 不同的γ值导致了较大差异的滤波效果.当γ值小于1时, 不但低频和高频部分被压制, 而且通带部分频率分量的能量也大幅度衰减, 这将导致时域中有效信号幅度的衰减, 因此较小γ值的LS-SVR滤波器不具有保幅性.另外γ值越小通带带宽越窄, 但通带的中心频率位置保持不变, 如图中线段AB所示, 这与图 4中通带范围的改变不同.因此在确定的核参数产生确定的通带中心频率和通带带宽的情况下, 可通过选择不同的γ值对通带带宽进行微调(通带中心频率保持不变), 但同时要注意其幅度的衰减, 采取适当的措施进行补偿.
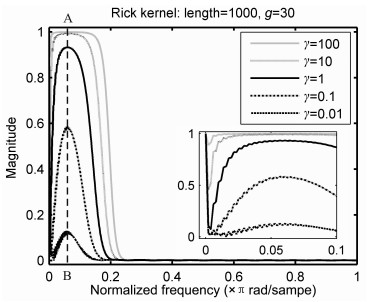
|
图 5 不同正则化参数的LS-SVR滤波器的频率响应随着正则化参数增大,滤波器通带变宽,但通带的中心频率基本保持不变,如线段AB所示. Fig. 5 Frequency responses of LS-SVR filters with different regularization parameters Passband of the filter gets wider with the regularization parameter increasing, but the central frequency nearly keeps constant as shown in Line AB. |
由滤波器长度、核参数和正则化参数对LS-SVR滤波器频率响应的影响分析可见, 滤波器长度影响着带通上升沿的陡峭性, 核参数值越大通带上升沿越陡; 核参数影响着通带的中心频率及通带带宽, 该值越大, 通带的中心频率越高, 且通带带宽越宽; 正则化参数影响着通带的带宽(通带中心频率随着该参数的改变基本保持恒定)和通带有效信号的幅度, 该值越小, 通带带宽越窄, 有效信号幅度衰减越严重.适当调整这三个参数的值可以产生具有不同中心频率和带宽的通带.
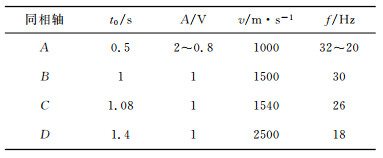
4 仿真实验本节通过仿真实验考察LS-SVR滤波器的去噪性能, 分别采用Ricker子波核和RBF核, 并与小波变换方法[15]和二维自适应Wiener滤波方法[15]进行比较.小波变换方法通过伸缩和平移等运算功能可对信号进行多尺度的细化分析, 在信号处理、故障诊断等领域已广泛应用.MATLAB图像处理工具箱提供的二维自适应Wiener滤波方法根据信号的局部方差来调节滤波器的输出, 但当噪声较强时适应性较差.图 6a显示了一含断层和薄层的合成地震记录, 其合成参数如表 1所示.其中轴A的地震子波的振幅和频率随着炮检距的增大而逐渐衰减.为了方便, 其他轴的子波振幅和频率保持不变.对该无噪声记录叠加入不同类型的随机噪声, 为方便起见, 1~20道叠加入高斯白噪声(均值为0, 方差为0.05), 21~30道叠加入脉冲噪声(密度10%, 振幅为1), 31~40道叠加入在区间[0, 0.2]上均匀分布的噪声, 形成如图 6b所示的受不同类型噪声污染的记录, 整张记录的平均信噪比(SNR: signal-to-noiseratio)为7.1067dB.由图 6b可见, 前20道噪声很强, 同相轴信息几乎淹没在噪声中.
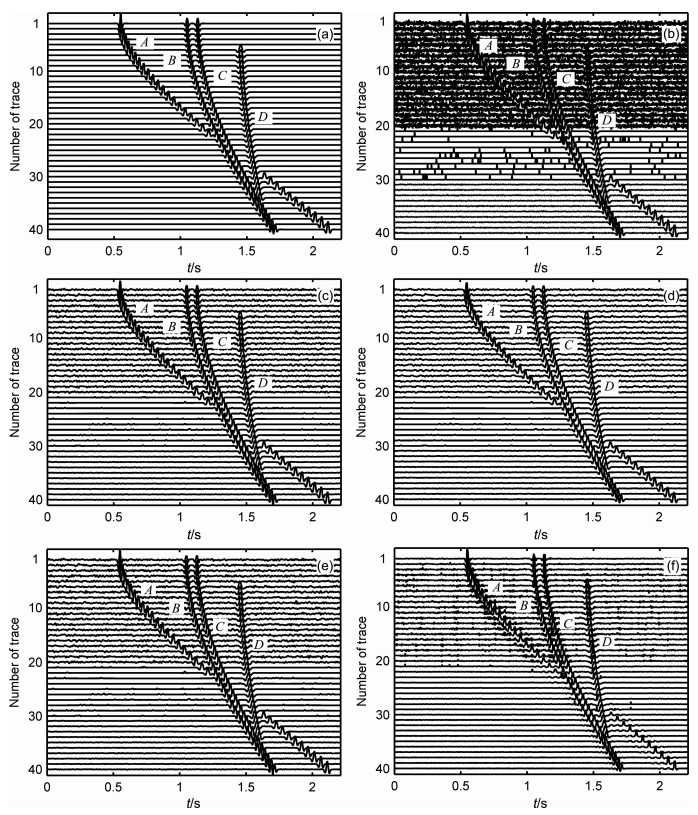
|
图 6 不同方法的滤波结果比较(A、B、C、D为同相轴) (a)无噪声记录; (b)噪声记录; (c) LS-SVR (Ricker核)滤波; (d) LS-SVR (RBF核)滤波; (e)小波变换滤波; (f)自适应Wiener滤波. Fig. 6 Comparison on results obtained by using different filtering methods (a) Clean record; (b) Noisy record; (c) Result by using the LS-SVR (Ricker kernel); (d) Result by using the LS-SVR (RBF kernel); (e) Result by using the wavelet transform-based method; (f) Result by using the adaptive Wiener filtering. |
|
|
表 1 模型参数 Table 1 Parameters of the model |
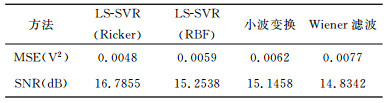
分别采用前述4种方法对如图 6b所示的噪声记录进行去噪处理, 对Ricker子波核LS-SVR滤波方法, 参数γ=1, g=30, 滤波器长度1000;对RBF核LS-SVR滤波方法, 参数γ=1, σ=0.0001, 滤波器长度1000;对小波方法, 采用sym8小波, 3级分解, 软阈值方法; 对Wiener滤波方法采用5×5窗口.处理结果分别如图 6(c~f)所示.显然, 经Ricker子波核LS-SVR滤波方法去噪后得到的记录中, 残留的噪声最弱, RBF核LS-SVR滤波方法稍强之, 小波变换方法对叠加了高斯白噪声的前20道记录中的噪声压制效果不如(c)和(d), Wiener滤波方法所得到的有效信号部分明显不如其他三种方法.表 2列出了四种方法去噪后计算得到的平均SNR以及与无噪声记录间的均方误差MSE.Ricker子波核LS-SVR滤波方法获得了最高的平均SNR以及最小的MSE.
|
|
表 2 不同方法滤波后的MSE和SNR Table 2 MSE and SNR obtained by using different filtering methods |
任取第20道记录, 利用傅里叶变换计算去噪前后的振幅谱, 如图 7所示.无噪声信号的有效频带约在[10, 50]Hz内, 含噪声信号在60 Hz以上很宽的无效频带内仍有较强的分量.经去噪处理后, Ricker子波核LS-SVR滤波方法得到记录的频谱分布(图 7c)最接近于原始无噪声信号的频谱分布(图 7a); RBF核LS-SVR滤波方法得到记录的频谱中, 由于RBF核具有低通性质因而保留了多余的低频分量(约0~5Hz), 其他频段与Ricker子波核相仿; 小波变换方法的低频段(约0~5 Hz)也未得到压制, 而且对[60, 90]Hz范围内的高频噪声压制得也不彻底; 与其他频谱图相比, 在有效频带内, Wiener方法得到的频谱能量明显低于其他方法, 且低频部分和高频部分压制的效果均较差.

|
图 7 不同方法去噪后频谱比较(第20道) (a)无噪声信号; (b)噪声信号; (c) LS-SVR (Ricker核)滤波; (d) LS-SVR (RBF核)滤波; (e)小波变换滤波; (f)自适应Wiener滤波. Fig. 7 Comparison on spectrums by using different filtering methods (trace 20) (a) Clean record; (b) Noisy record; (c) Result by using the LS-SVR (Ricker kernel); (d) Result by using the LS-SVR (RBF kernel); (e) Result by using the wavelet transform-based method; (f) Result by using the adaptive Wiener filtering. |
从上述时域及频域的比较可见, 在地震资料处理中, Ricker子波核LS-SVR滤波器的去噪能力优于RBF核LS-SVR滤波器以及其他诸如小波变换和Wiener滤波器等常用的滤波器.
5 结论针对利用LS-SVM去除随机噪声这一问题, 本文证明了平移不变类核LS-SVR滤波系统是一个线性时不变系统, 不同的核函数具有不同的滤波特性, 如Ricker子波核具有带通性质, RBF核具有低通性质.不同的参数影响着滤波器不同方面的性质, 对于Ricker子波核, 滤波器长度影响着带通上升沿的陡峭性; 核参数影响着通带的中心频率及通带带宽; 正则化参数影响着通带的带宽和通带有效信号的幅度, 可以根据信号处理的要求, 适当调整这三个参数以达到所期望的滤波效果.合成地震记录的仿真实验表明, Ricker子波核LS-SVR滤波器在地震勘探信号的去噪应用中, 滤波性能优于RBF核LS-SVR滤波器以及小波变换滤波和Wiener滤波方法.
| [1] | Ulrych T J, Sacchi M D, Graul J M. Signal and noise separation:art and science. Geophysics , 1999, 64(5): 1648-1656. DOI:10.1190/1.1444670 |
| [2] | Walden A T. Robust deconvolution by modified Wiener filtering. Geophysics , 1988, 53(2): 186. DOI:10.1190/1.1442453 |
| [3] | Liu Y, Liu C, Wang D. A 1D time-varying median filter for seismic random, spike-like noise elimination. Geophysics , 2009, 74(1): 17-24. |
| [4] | 刘洋, FomelSergey, 刘财, 等. 高阶seislet变换及其在随机噪声消除中的应用. 地球物理学报 , 2009, 52(8): 2142–2151. Liu Y, Fomel Sergey, Liu C, et al. High order seislet transform and its application of random noise attenuation. Chinese J. Geophys. (in Chinese) , 2009, 52(8): 2142-2151. |
| [5] | 张中杰. 多分量地震资料的各向异性处理和解释方法. 哈尔滨: 黑龙江教育出版社, 2002 . Zhang Z J. Anisotropy Processing and Interpretation of Multicomponent Seismic Data (in Chinese). Harbin: Heilongjiang Educational Press, 2002 . |
| [6] | Zhang Z J, Wang G J, Teng J W, et al. CDP mapping to obtain the fine structure of the crust and upper mantle from seismic sounding data:An example for the southeastern China. Phy. Earth Plant. Interiors , 2000, 122: 133-146. DOI:10.1016/S0031-9201(00)00191-6 |
| [7] | Vapnik V N. The Nature of Statistical Learning Theory. New York: Springer-Verlag, 1995 . |
| [8] | Li D L. Support vector regression based image denoising. Image and Vision Computing , 2009, 27: 623-627. DOI:10.1016/j.imavis.2008.06.006 |
| [9] | Wu D X, Peng D Q, Tian J W. Image denoising using local adaptive least squares support vector regression. Geo-Spatial Information Science , 2007, 10(3): 196-199. DOI:10.1007/s11806-007-0083-3 |
| [10] | 邓小英, 杨顶辉, 刘涛, 等. Ricker子波核支持向量回归的Mercer条件拓展问题研究. 地球物理学报 , 2009, 52(9): 2335–2344. Deng X Y, Yang D H, Liu T, et al. Study on Mercer condition extension of support vector regression based on Ricker wavelet kernel. Chinese J. Geophys. (in Chinese) , 2009, 52(9): 2335-2344. |
| [11] | Cheng H, Tian J W, Liu J, et al. Wavelet domain image denoising via support vector regression. Electronics Letters , 2004, 40(23): 1479-1480. DOI:10.1049/el:20046567 |
| [12] | Mercer J. Functions of positive and negative type and their connection with the theory of integral equations. Philosophical Transactions of the Royal Society of London (Series A) , 1909, 209: 415-446. DOI:10.1098/rsta.1909.0016 |
| [13] | Smola A J, Sch lkopf B, Müller K-R. General cost functions for support vector regression. Proc. of the 8th Int. Conf. Artificial Neural Networks, Australian, 1998. 79~83 |
| [14] | Cherkassky V, Ma Y Q. Practical selection of SVM parameters and noise estimation for SVM regression. Neural Networks , 2004, 17: 113-126. DOI:10.1016/S0893-6080(03)00169-2 |
| [15] | The MathWorks Inc. MATLAB, The language of Technical Computing. Version 7.0.0.19920(R14), 2004 |
 2010, Vol. 53
2010, Vol. 53