2. 清华大学数学科学系, 北京 100084;
3. 中国石化胜利石油管理局钻井工艺研究院, 山东东营 257017
2. Department of Mathematical Sciences, Tsinghua University, Beijing 100084, China;
3. Drilling Technology Research Institute, Shengli Petroleum Administration Bureau, Shandong Dongying 257017, China
在石油钻井中, 几千米钻柱是井底和地面信息传递通道, 钻头破岩振动沿钻柱传播到地面, 通过分析钻柱顶部测量获得的振动信息, 可以为随钻地震(SWD)数据处理提供钻头源信号, 开展井下诊断, 获得所钻地层特性、钻头磨损情况和钻柱的转动情况.
利用钻井过程中的钻头破岩所发射出的地震波, 进行随钻地震探测, 可以实现钻前预测.1936年, Weatherby [1]提出了利用钻头信号作为震源的想法, 但由于当时技术水平的限制, 该想法未能得到发展.20世纪六、七十年代, 人们发现牙轮钻头信号的能量和频带宽度足够被用作震源, 随钻地震(Seismic While Drilling)方法的研究才又引起了重视[2~9].从目前的技术看, 直接测量钻头源的信号难度较大, 一般是利用在井架上的加速度传感器记录信号, 通过记录到的参考信号来获取钻头信号.参考信号大体上由来自钻头的信号构成, 但是钻头信号经过钻柱时, 钻柱的滤波效应以及多次波很强的混叠效应使得钻头信号有很大的"失真"[10].消除这些影响, 恢复钻头源信号, 作为与地面记录互相关的源函数, 是随钻地震信号处理的一个关键步骤[11~13].
倒谱分析是由Borgert等[14](1963)提出并用于混响信号处理的一项技术, 它的突出优点是对信号传递路径和测点位置的影响不灵敏, 所以其在传播路径及系统识别、机器故障识别等方面具有独特的应用[15, 16].倒谱分析能解决自相关函数或功率谱有时不能解决的问题, 在这些问题中, 各信号分量在时域内是卷积关系, 而非简单的线性叠加, 通过倒谱分析能将其变换为线性相加关系, 利用窗函数进行倒时域的滤波, 即可分离信号分量.由于钻头信号沿钻柱的传播是典型的卷积和混响问题, 倒谱技术可以用于钻头信号的分离[17~19].本文针对沿钻柱传播的随钻地震钻头信号受到的干扰大, 信号难以提取的情况, 利用倒谱方法的非线性滤波原理, 对信号进行结构混响的去除, 消除传递路径的影响, 强化钻头信号特征, 为随钻地震数据后续处理打下基础.
2 方法原理 2.1 随钻地震参考信号的复倒谱分析随钻地震由钻柱顶端安装加速度传感器, 记录钻头发出的信号.为了研究方便, 一般假设钻柱系统为一线性系统, 由于钻柱结构混响以及传递路径等因素的影响, 在钻柱顶端接收到的钻头信号已经受到严重干扰, 即钻柱顶端记录的参考信号p(n)为钻头发出的信号b(n)与钻柱传递路径等因素h(n)的卷积:
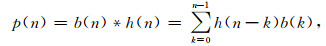
|
(1) |
由此我们可以得到式(1)的倒频谱为
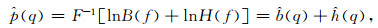
|
(2) |
其中, B(f), H(f)依次为钻头信号和钻柱传递路径的频谱, 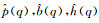
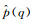
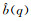
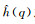
由于复倒谱变换保留了信号的振幅和相位信息, 有利于我们对激励源信号也即钻头信号进行提取, 因此能重建信号, 满足钻柱波传播中的源信号的提取要求.但在实际应用中会出现一些不可忽视的问题, 如溢出错误、窗函数的选择以及相位展开等问题[21].例如相位展开问题, 是由于利用复倒谱变换对信号进行分析的过程中, 测得的参考信号p(n)经过复倒谱分析后, 其虚部即相位函数, 得到的不再是主值相位连续曲线, 造成相位折断, 因此需要引入相位校正序列, 在相邻两相位变化不会大于π的原则下, 对相位进行相位展开和去均势项处理, 恢复相位的连续性.
2.2 倒频谱域信号分离基本思路倒频谱是将对数谱图上周期性频率结构成分的能量做了又一次集中, 在频率的对数转换时给低幅值分量有较高的加权, 而对高幅值分量以较低的加权, 结果使小周期信号在倒频谱图中得到了突出.对参考信号进行复倒谱分析的目的是要分离卷积信号, 一般须采用非线性滤波的方法也即倒谱滤波分析方法, 可利用一个非负的平滑窗对复倒谱进行处理, 从而得到期望的倒谱分量.选择一个"倒滤波矩形窗"W(q)将需要的倒谱分量挑出, 即:
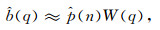
|
(3) |
式中W(q)具有如下形式:
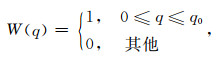
|
(4) |
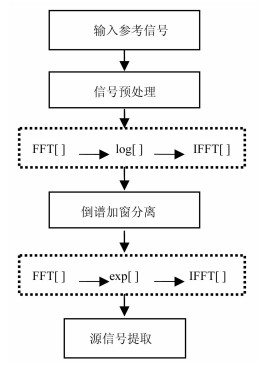
其中q0为振源和传递途径在自倒谱域上的截断点, 该值大小可视具体情况而定.采用矩形窗对参考信号的复倒谱进行滤波分离是一种较为简便的方法, 但倒谱中不存在用线性滤波器直接分离的低倒时或高倒时成分时, 经过傅里叶变换后矩形窗将在高频产生误差, 从而在反傅里叶变换到时间域时产生能量泄漏现象, 所以在进行倒谱加窗滤波时, 要根据数据的情况选择不同的窗函数, 如海明窗(Hamming)、高斯窗(Gaussian)等.分离后的信号作傅里叶正变换、指数运算和傅里叶反变换等数学逆变换下, 将分离的信号返回到时域, 从而实现源信号的提取.倒谱分析滤波的示意图见图 1.
|
图 1 利用复倒谱分析方法进行源信号提取的流程 Fig. 1 Flow chart of abstracting the source signals using the complex cepstrum analysis |
首先利用钻柱模拟实验数据进行上述倒谱算法验证.钻柱模拟实验的模型是由线性稳态系统(钢管), 受到一个瞬态随机激励源信号(力锤激发信号)所产生的响应.钢管连接模型如图 2所示, 左端5.08cm钢管一端用钢堵头封堵作为力锤敲击接触面, 将三分量传感器用磁座吸附在两端, 将力锤(激发信号)与传感器三个分量通过传感器线输入多功能数据采集(奥地利德维创公司), 采样频率为5000 Hz.每个传感器分别接收了2次不同源(钢锤头、尼龙锤头)的敲击信号, 为瞬态随机激励.本次数据分析从最长管柱、单脉冲测量数据开始, 即取第五组数据的最后一个传感器接收的信号为例进行倒谱分析.为便于使用快速傅里叶变换, 采样长度为1024个点.因为力锤道信号有接收, 故可得到锤道信号也即源信号, 不同源原始信号和传感器接收到的振动响应信号及其频谱如图 3所示(以钢锤头信号为例).从图中可以看出, 钢锤头随机激励源信号频率范围较宽; 而响应信号频谱具有许多峰谷, 它们来自振动传输中的模态响应.

|
图 2 实验钢管连接模型(其中星星位置为检波器位置) Fig. 2 The model of steel tube connection (The stars indicate the position of detectors) |
|
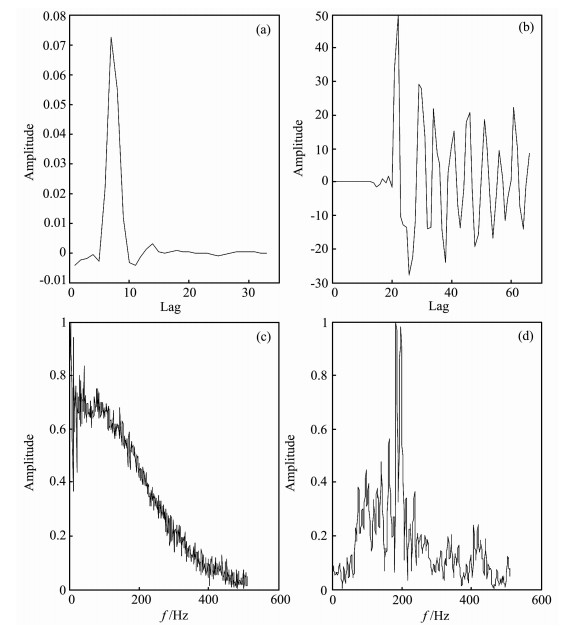
图 3 钢锤帽力锤敲击后的源信号和传感器接收到的振动响应信号及其频谱 (a)钢锤头敲击后的锤道信号; (b)钢锤头敲击后的响应信号; (c)锤道信号频谱; (d)响应信号频谱. Fig. 3 Excitation signal of the steel hammerhead and the steel tube vibration and which after the FFT transform (a) Excitation signal of the steel hammerhead; (b) Excitation signal of the steel tube; (c) Frequency spectrum of the hammerhead; (d) Frequency spectrum of the response signal. |
采样长度为1024个点.因为力锤道信号有接收, 故可得到锤道信号也即源信号, 不同源原始信号和传感器接收到的振动响应信号及其频谱如图 3所示(以钢锤头信号为例).从图中可以看出, 钢锤头随机激励源信号频率范围较宽; 而响应信号频谱具有许多峰谷, 它们来自振动传输中的模态响应.
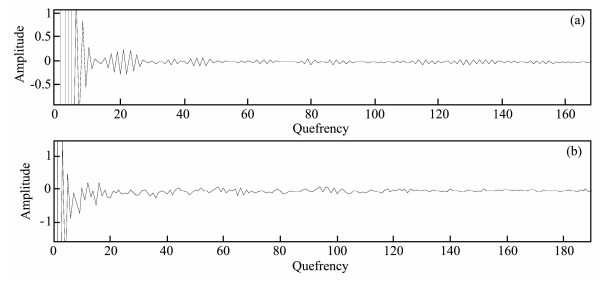
首先对图 3a和图 3b中的信号进行开时窗、去均值等预处理, 并求得预处理之后的复倒谱如图 4所示.因为复倒谱系数左右对称, 故图中仅取左半边部分系数.从图 4可以看出, 力锤敲击得到的锤道信号由于其持续时间很短, 一般作为瞬态信号来处理, 它的复倒谱主要集中在低时部分, 对其进行低通滤波, 可以有效消除测量路径和其他激励源等因素的影响, 从而实现激励源信号的混响解调; 对于响应信号, 由于传递路径很短, 激励源信号和传递路径的平均特性都集中在倒谱的低时部分.即低时部分的第一个部分是由瞬态锤击信号周期变化引起的, 第二部分是传递函数的平均特性; 倒谱的高时部分主要由传递函数的结构混响引起.
|
图 4 图 3中源信号和传感器接收到的响应信号的复倒谱 (a)锤道信号经过复倒谱变换后; (b)响应信号经过复倒谱变换后. Fig. 4 Complex cepstrum transform of the excitation signal and the response signal (a) Complex cepstrum transform of the excitation signal; (b) Complex cepstrum transform of the response signal. |
对响应信号的复倒谱进行低通滤波, 可消除结构混响.
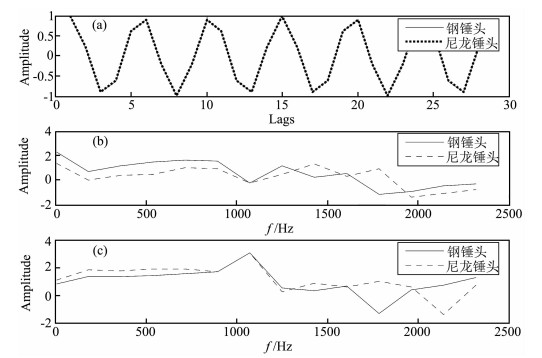
对图 4中的信号进行开高斯窗处理, 开窗长度为28个采样点, 得到开窗之后的源信号和响应信号倒谱, 两者的相位要进行相位展开处理.在频域中将两者相减, 得到传递函数及其幅值和相位如图 5所示.将钢锤头激发信号和尼龙锤头激发源信号进行对比, 两者的传递函数波形重合, 两者传递函数的幅值和相位存在差别, 但是差别非常小, 这种差别是由于不同源激发导致的.
|
图 5 不同源激发得到的传递函数波形及幅值相位图 (a)传递函数波形; (b)传递函数波形幅值图; (c)传递函数波形相位图. Fig. 5 Wave profile of the transfer function from the different source excitation and their amplitude and phase (a) Wave profile of the transfer function; (b) Amplitude profile of the transfer function; (c) Phase profile of the transfer function. |
因为倒谱加窗减小了相同结构中传递函数的变化性, 通过倒谱加窗求得的传递函数可作为同组结构的通用传递函数.提取图 5中的源信号与原始锤道信号进行对比见图 6.由于经过了高斯加窗处理, 复倒谱分析不能恢复精确的源信号, 但是根据恢复信号的幅值、宽度, 能给出源信号的一个初步的估计.

|
图 6 不同源锤道信号恢复 (a)钢锤头源信号恢复; (b)尼龙锤头源信号恢复. Fig. 6 Reconstructing a signal fromthe different excitated sourcesand the steel tube vibration and which after the FFT transform (a) Reconstructing a signal from excitated signal of the steel hammerhead; (b) Reconstructing a signal fromexcitated signal of the nylon hammerhead. |
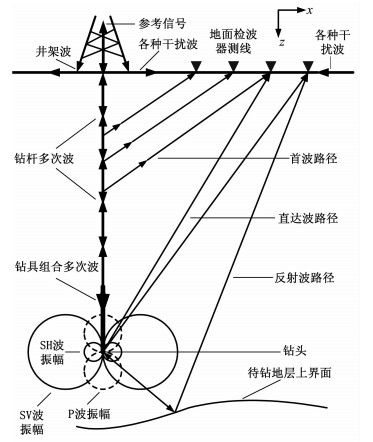
随钻地震波场复杂, 包括井架波、首波、钻杆多次波、钻具组合多次波等(如图 7).随钻地震的一般做法是在钻柱顶端安装加速度传感器, 记录来自钻头的信号, 再和地表布设的地震计的记录做相关和叠加处理, 得到钻头前方的地震图(如图 8).参考信号通常指安装在钻柱顶端的加速度传感器记录的信号, 它的垂向分量主要由来自钻头的信号构成, 但也有很多干扰存在[11], 主要包括转盘旋转造成的钻柱振动、泥浆泵的振动、井场其他机械的振动等.消除各种噪音和钻柱滤波效应的影响, 尽量提取到来自钻头的有效信号, 是随钻地震信号处理的关键.
|
图 7 随钻地震波场示意图 Fig. 7 The diagram of the SWD wavefield |
|
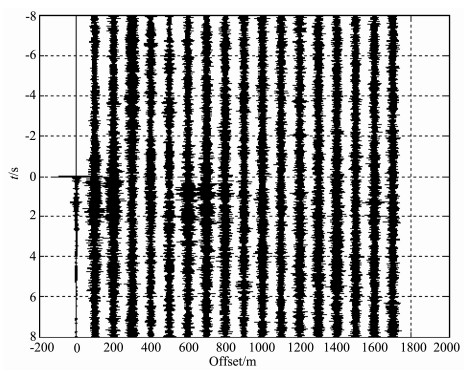
图 8 未经过倒谱分析的钻头前方的地震图(0道为参考信号道) Fig. 8 The seismogram of not having the cepstrum analysis (the zero trace is the pilot signal) |
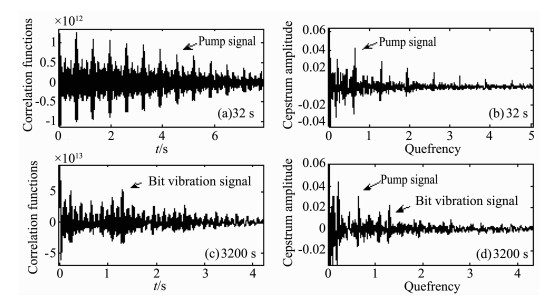
本文分析的实例是对某井钻井深度约3100 m时记录的参考信号, 数据长度3200s, 采样率500Hz.其中钻柱多次反射波是周期性最稳定的成分, 泵冲是参考信号中能量强的成分.纵波在钻柱内的波速约为4750m/s, 一次反射波的时延为1.3s左右; 另外由录井资料可知, 泵冲周期为0.65s.钻柱多次反射波和泵冲信号的周期时延是非常接近的, 为将二者区别开来, 根据短时间数据的自相关函数可以凸显能量强的周期性成分, 也即泵冲信号; 长时间数据的自相关函数可以凸显周期性稳定的成分的也即钻柱多次波[10].分别取时间长度为32s和3200s的数据进行倒谱分析, 并与数据自相关记录进行比较(见图 9).可以很清楚看到短时间数据(32s)主要显示出了强能量的泵冲信号(见图 9a, 图 9b), 而长时间数据(3200s)主要显示出了稳定的钻柱反射波周期信号(见图 9(c, d)).而图 9b、图 9d相对于图 9a、图 9c而言, 很好地压制了混叠现象, 更清晰地突出了钻头振动微弱信号周期性时间结构成分.
|
图 9 不同长度参考信号自相关函数和倒谱分析(仅取大于零的部分) (a)32s长参考信号自相关函数; (b)32s长参考信号倒谱分析; (c)3200s长参考信号自相关函数; (d)3200s长参考信号倒谱分析. Fig. 9 Auto-correlation functions of pilot in different time length and which after the cepstrum analysis (only retains the data of more than zero) (a) Autocorrelation functions of pilot in 32 s; (b) Cepstrum analysis of pilot in 32 s; (c) Auto-correlation functions of pilot in 3200 s; Frequency spectrum of the hammerhead; (d) Cepstrum analysis of pilot in 3200 s. |
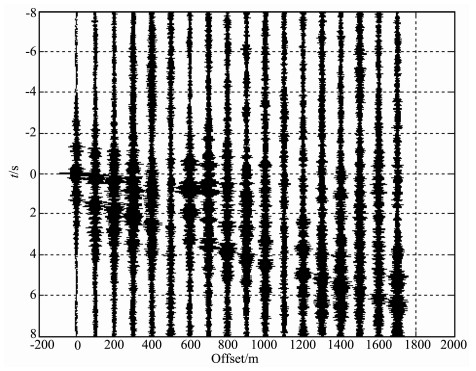
由于我们认为钻柱多次反射波为有效波, 所以用时间长的信号进行倒谱分析突出钻柱多次反射波.利用倒滤波窗, 对图 9d的倒谱分析进行倒谱加窗低通滤波, 去除了结构混响, 强化了钻头信号的特点.将得到的源信号与地面的记录做相关和叠加处理, 得到地震剖面如图 10, 与图 8相比, 可以得到较清楚的面波和直达波震相, 信噪比高于没有经过倒谱分析处理的结果.
|
图 10 经过倒谱分析的随钻地震处理 Fig. 10 The SWD processing after the cepstrum analysis |
由于随钻地震的复杂性, 参考信号的周期成分也很多, 另外机械噪音也多是周期性的, 所以对随钻地震参考信号进行倒谱分析存在着钻柱响应和钻头多次反射波的倒谱并不能总是分离的问题, 即使能分离, 其分离点也难确定, 因此很难得到满意的效果, 还需要与其他处理方法如独立分量分析等相结合才能得到有效钻头信号[10].
4 结论及讨论卷积传递过程可以利用倒频谱将时域里的卷积问题转化为频域里的相加问题, 有助于将源信号与传递函数加以分离, 从而恢复源信号和传递函数.本文将倒谱分析技术用于分析弹性波沿管柱的传播问题.分析表明倒谱有助于压制管柱传播过程中的混响, 可用于恢复源函数和传递函数.
(1) 利用室内模拟实验验证了倒谱分析技术的可靠性, 压制了管柱混响, 获得源信号和传递函数;
(2) 去噪的基础上, 利用倒谱对钻柱顶部接收到的振动信号进行了分析, 压制了长周期混响, 突出了信号中的周期特征, 为分析钻头微弱振动和传播特征分析提供了条件;
(3) 将提取的钻头源信号与地面记录互相关, 提高了随钻地震数据处理的信噪比, 为SWD数据处理提供了一条可行之路;
(4) 钻柱模拟实验中, 倒谱分析虽然不能恢复精确的源信号, 但是根据恢复信号的幅值、宽度, 能给出瞬态源信号的一个初步估计.
| [1] | Weatherby B B.Method of making sub-surface determinations.U S Patent, 1936.2 |
| [2] | Deily F H, Dareing D W, Paff G H, et al. Downhole measurements of Drill String Forces and Motions. Transaction of American Society of Mechanical Engineering for Industry , 1968: 217-225. |
| [3] | Lutz J, Raynaud M, Gstalder S, et al. Instantaneous logging based on a dynamic theory of drilling. Journal of Petroleum Technology , 1972, 24: 750-758. DOI:10.2118/3604-PA |
| [4] | Rector J W. Utilization of drill-bit vibrations as a downhole seismic source. California: Stanford University, 1990 . |
| [5] | Clement K. Multichannel seismic experiment with a drill-bit source.Stanford University, 1990 |
| [6] | Rector J W, Marion B P. The use of drill-bit energy as a downhole seismic source. Geophysics , 1991, 56: 628-634. DOI:10.1190/1.1443079 |
| [7] | Meehan R, Haldorsen J. Rekindling Interest in Seismic While Drilling. Oilfield Review, Jan , 1993: 4-13. |
| [8] | Jaob B, Haldorsen U, Douglas E, et al. Walkaway VSP using drill noise as a source. Geophysics , 1995, 60(4): 978-997. DOI:10.1190/1.1443863 |
| [9] | Flavio P, Trieste, Milano. Seismic while drilling use of pilot signals with downhole motor drilling. SEG Expanded Abstracts , 1998, 17: 147-150. |
| [10] | 陆斌, 葛洪魁, 吴何珍, 等. 利用相关域小波变换进行SWD资料预处理. 地球物理学报 , 2009, 52(9): 2349–2356. Lu B, Ge H K, Wu H Z, et al. SWD data preprocessing using wavelet transform of correlation domain. Chinese J. Geophys. (in Chinese) , 2009, 52(9): 2349-2356. |
| [11] | Poletto F, Malusa M, Miranda F. Numerical modeling and interpretation of drillstring waves. Geophysics , 2001, 66: 1569-1581. DOI:10.1190/1.1487102 |
| [12] | Flavio P, Francesco M. Seismic while drilling fundamentals of drill-bit seismic for exploration. Handbook of Geophysical Exploration , 2004: 35. |
| [13] | 张绍槐, 韩继勇, 朱根法. 随钻地震技术的理论及工程应用. 石油学报 , 1999, 20(2): 67–72. Zhang S H, Han J Y, Zhu G F. The engineering application and theory of seismic while drilling. Acta Petrolei Sinica (in Chinese) , 1999, 20(2): 67-72. |
| [14] | Borgert B P, Healy M J, Tukey J W. The quefrency analysis of time series for echoes:cepstrum, pseudo-autocovariance, cross-cepstrum and saphe craking:Proc. Symp. On Time Series Analysis, Rosenblatt, M.Ed.:John Wiley and Sons, Inc. , 1963: 209-243. |
| [15] | 郝志勇, 舒歌群, 薛远, 等. 内燃机气缸压力振动识别研究. 内燃机学报 , 1994, 112(1): 43–48. Hao Z Y, Shu G Q, Xue Y, et al. An investigation of identifying cylinder pressure of I.C.Engine by vibration measurement. Transactions of CSICE (in Chinese) , 1994, 112(1): 43-48. |
| [16] | Ulrych T J. Application of homomorphic deconvolution to seismology. Geophysics , 1971, 36: 650-660. DOI:10.1190/1.1440202 |
| [17] | Oppenheim A V, Schafer R W. Digital Signal Processing. New Jersey: Prentice-Hall, 1975 . |
| [18] | Drumheller D S. Attenuation of sound waves in drill strings. J.Acoust. Soc.Am. , 1993, 94(4): 2387-2396. DOI:10.1121/1.407458 |
| [19] | Macpherson J D, Jogi P, Baker Hughes Inteq, et al. Application and analysis of simultaneous near bit and surface dynamics measurements. 1998, IADC/SPE 39397 |
| [20] | 梁凤岗, 徐敏. 瞬态信号波形重构及其应用. 哈尔滨工程大学学报 , 1997, 18: 20–27. Liang F G, Xu M. Waveform reconstruction of transient signal and its application. Journal of Harbin Engineering University (in Chinese) , 1997, 18: 20-27. |
| [21] | 钱济国. 倒谱分析及其在机械故障诊断中的应用. 动态分析与测试技术 , 1996, 4: 30–33. Qian J G. Cepstrum analysis and its application in machine fault diagnosis. Dynamic Analysis and Testing Technology (in Chinese) , 1996, 4: 30-33. |
 2010, Vol. 53
2010, Vol. 53

