2. 中国石油集团测井有限公司, 西安 710021
2. China Petroleum Logging Co. Ltd., Xi'An 710021, China
渗透率反映着地层的流体传输能力, 是评价石油、天然气储层可开采特性的重要参数之一.因此, 准确快速了解地层渗透率信息, 对于油田勘探开发具有重要意义.当前使用最广泛的渗透率评价方法是通过声波测井、中子测井和密度测井获得地层孔隙度, 再利用所在油田区块岩芯实验获得的孔隙度-渗透率经验关系, 估计地层渗透率[1].但这种方法不是基于物理原理, 而是依据统计学公式和实验经验.通过核磁共振驰豫时间评价地层渗透率[2]和斯通利波幅度的衰减评价地层渗透率[3], 具有明确的物理原理支撑, 是目前相对先进的渗透率测井方法, 但由于影响因素较多, 测量精度并不高.利用地层测试器(MDT)测量地层渗透率[4], 是当前最可靠的原地渗透率测量方法, 但不是连续测量方法, 且测量成本高.此外, 还有人提出利用电法测井, 根据冲洗带、侵入带、原状地层三种电阻率的差异, 推测地层渗透率.总之, 目前还缺少能准确进行井下连续测量渗透率的技术.
以上方法都是单独利用声学、电磁学、力学或核物理学的测量方法.然而, 由测量渗透率的众多方法可知, 渗透率与地层的多种物理参数均有关系, 这意味着渗透率可能反映着某些物理量之间的耦合能力, 可否利用这些耦合效应来实现对渗透率的测量是值得探索的.
国际上已有研究表明, 在实验室内利用固-液间的动(声)电效应可测量地层渗透率[5, 6], 并提出了在井下通过声电效应测井(也称震电测井)测量地层参数的设想[7~11].这种测井方法以孔隙介质的动电耦合现象为基础, 利用声信号和电信号在孔隙地层中的相互转换, 获得含有反映介质特性信息的信号, 从而实现对渗透率等地层参数的测量.Zhu等[8]最早在小型模型井中观测到了声波诱导的电磁场; 胡恒山等[12]采用江汉油田全直径岩芯制作的模型井, 也观测到了声电转换信号, 并考察了渗透率等地层参数对波场的影响.刘洪等[13]分析了电磁波对声电参数的分辨力, 并多次参与声电效应现场试验.石昆法[14]在室内观测了含油、含水砂岩以及粘土和砂土模型中的震电转换信号, 并对测试结果进行了比较分析.陈本池等[15]进行了模型井中震电转换实验观测.针对声电效应测井模型, 胡恒山等[16]基于Pride方程组, 通过引入位移和电场的标量和矢量势函数, 推导出了声场和电磁场的计算公式, 模拟了声电效应测井的全波波形.崔志文[17]采用全耦合的Pride方程组计算了多级源激发的声电耦合场.关威等[18]先计算井中多级声源激发的声场, 再通过引入赫兹势求解了声诱导的电磁场.
但是, 我国目前还没有利用动电效应测量渗透率的相关实验设备, 人们对于利用岩石动电效应进行勘探也尚存疑义.另一方面, 当前实验室测量渗透率主要采用气测方法, 该方法也存在一定的局限性, 如高雷诺数情况下的湍流效应等[19].鉴于渗透率对油气勘探的重要性, 寻找新的渗透率实验测量方法, 作为气测方法的补充是有意义的.此外, 天然地震诱导电磁场的现象日益受到地球物理学界的关注, 而岩石动电效应是引起地震电磁场的因素之一, 因此要定量分析地震波诱导电磁场的强弱和分布情况[20], 必须以岩芯动电耦合实验为基础.鉴于此, 我们进行了动电实验研究, 开展了动电渗透率测量设备的研制工作, 并且利用动电实验参数获得了地层渗透率.
2 渗透率动电理论相互接触的两相体系(如固-液体系)因界面上电荷分离而带电, 使异号电荷分布在界面两侧, 构成双电层结构[21].由于固-液两相间的双电层结构, 若用外力作用使两相发生相对运动, 则沿运动方向将产生电场; 同样, 当外界电场存在时, 两相将发生相对运动.这些效应统称为力(动)-电(磁)耦合效应或动电效应.动电效应包括流动电势、电渗、震电效应等.Pride[7]依据物理学原理, 导出了用于描述孔隙介质动电效应的动电耦合方程组.在频率很低, 惯性力可以忽略的情况下, 弹性场和电磁场的耦合表示为
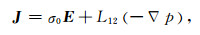
|
(1) |
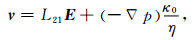
|
(2) |
其中, J是电流密度矢量, E是电场强度矢量, p是孔隙流体压强, η是孔隙流体黏度, σ0是压力梯度为零时孔隙介质的电导率, κ0是电场为零时的渗透率.v是渗流速度矢量, L12和L21称为动电耦合系数.
依据(1)和(2)两式, 我们定义两个实验参数[5]:流动电势系数KS和电渗压力系数KE.KS是流动电势实验中, 当流过岩样的电流密度为零时, 岩样两端的电位差ΔΦ与作用于岩样两端的流体压强差Δp之比的负值.KE是电渗实验中, 当通过岩样的渗流为零时, 岩样两端的压强差Δp与作用于岩样两端的电位差ΔΦ之比的负值.由于定常和拟静态情况下, E=-▽Φ, 可用(Δ/岩样长度)代替▽, 故
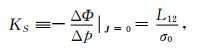
|
(3) |
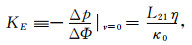
|
(4) |
由Onsager互易关系知, L12=L21=L, 所以, 通过(3)和(4)两式可得岩芯动电渗透率,
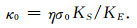
|
(5) |
因此, 岩芯渗透率的动电测量理论包括流动电势和电渗两种动电效应.通过流动电势和电渗实验, 获得岩芯电导率σ0、流动电势系数KS和电渗压力系数KE, 便可依据(5)式计算出岩芯动电渗透率.
3 岩芯动电渗透率实验测量 3.1 岩样制备及岩芯夹持器实验中使用岩芯样品的孔隙度在20%~30%之间.样品均为直径1英寸(1英寸=25.4 mm)的圆柱体岩芯, 长度为2cm.岩芯样品在使用前要进行清洗, 先洗掉杂质, 然后用四氯化碳洗油, 无水乙醇洗盐.另外, 气泡的存在会对实验结果产生很大影响[21], 所以必须对岩芯进行抽空及完全饱和.实验中使用的NaCl溶液浓度为0.05mol/L.
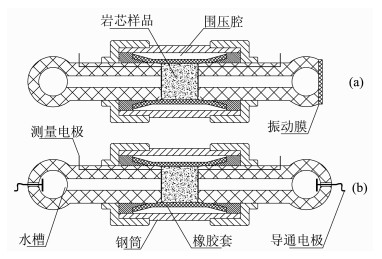
由于流动电势和电渗实验机理不同, 所以根据实验需要设计了两套岩芯夹持器, 见图 1, 分别用于流动电势和电渗实验.夹持器主要由两端圆柱体水槽和水平钢筒构成.水槽用有机玻璃制作, 容积约为17mL, 与水平钢筒用螺纹连接, 这样方便岩芯安装和拆卸.岩芯两端以及水槽内电极均为Ag/AgCl电极[22], 电极通过电化学方法制作, 并依据其不同功能定义为测量电极和导通电极.为了保证液流、电流只从岩芯内部而不从岩芯外侧柱面流过, 夹持器专门设计了一套围压装置, 本文之前没有见过类似的设计.实验中将高压气体从进气口注入围压腔内, 并保持围压1.2MPa, 使橡胶套管紧紧"握住"岩芯, 从而迫使液流、电流只能从岩芯内部通过.此外, 围压还起到严格的密封作用, 以确保水槽与钢筒连接处不会漏水、漏气.夹持器使用刚性材料(有机玻璃和不锈钢)制作, 因而实验中不存在装置材料可压缩性引起的误差.
|
图 1 动电实验夹持器设计图 (a)流动电势实验;(b)电渗实验. Fig. 1 The core holders for electrokinetic experiments (a) Streaming potential experiment; (b) Electroosmotic experiment. |
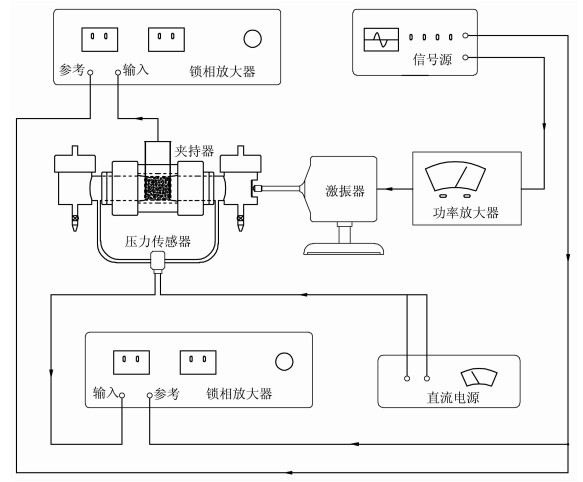
图 2, 图 3分别为流动电势和电渗实验测量系统原理图, 两套系统的主要差别是激励源对夹持器中岩芯的作用方式不同.流动电势实验中, 信号源输出低频信号经功率放大器放大之后供给激振器, 促使与其紧密接触的振动膜作周期振动, 进而在岩芯两端形成压强差.电渗实验中, 信号源给交流电流源低频激励, 使其产生一个与信号源同频的电流, 电流通过导通电极流过岩芯, 并在岩芯两端形成电位差.虽然两个实验的激励方式不同, 但都是在系统平衡后, 测量岩芯两端的电位差和压强差.电位差由岩芯两端的Ag/AgCl测量电极引出, 压强差用差压传感器检测.根据压差大小, 实验使用两种差压传感器26PC (10VDC, 1psi)和DC001(5VDC, 250Pa), 分别用于流动电势和电渗实验.但由于这些信号非常微弱, 甚至周围噪声都可将其淹没, 所以实验选用专门的微弱信号检测仪器---锁相放大器(SR830), 它能够检测埋藏于噪声中微弱信号, 是动电测量系统的关键仪器[23].
|
图 2 流动电势实验测量系统原理图 Fig. 2 The scheme of streaming potential test system |
|
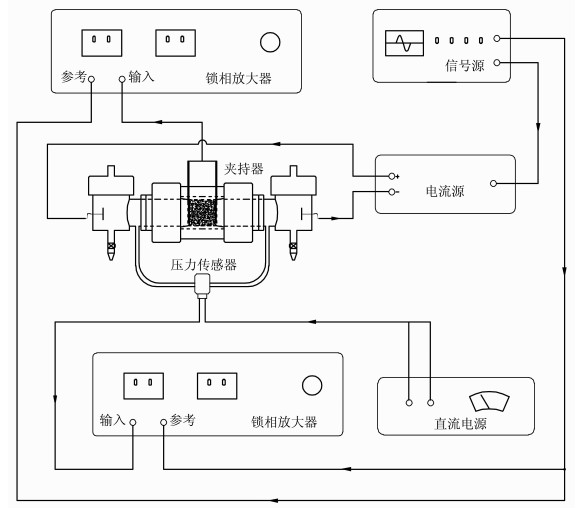
图 3 电渗实验测量系统原理图 Fig. 3 The scheme of electroosmosis test system |
实验使用两台锁相放大器同步测量岩芯两端的电位差和压强差, 并利用锁相放大器检测电流的功能来测量电流, 然后根据(3), (4)两式确定流动电势系数KS和电渗压力系数KE, 再依据电学知识换算岩芯电导率σr, 进而由(5)式计算得出岩芯渗透率.本文流动电势实验中, 功放的工作电压为3V, 得到电位差为几十微伏, 电流为几十纳安, 压强差为几千帕.电渗实验中, 电流源输出约为1 mA, 压强差为几百毫帕.
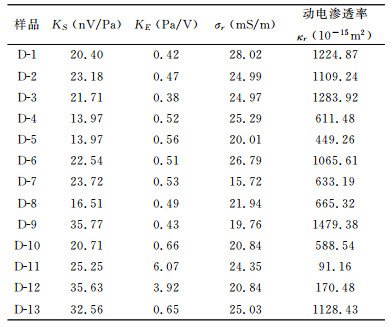
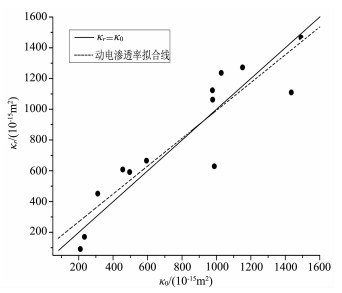
4 实验结果与分析表 1是13块岩芯的物理参数表, 表 2是利用(5)式获得的岩芯动电渗透率测试结果, 其中黏度η=0.9mPa·s.图 4比较了气测渗透率和动电渗透率测量结果的差异, 虚线是由动电渗透率与气测渗透率对比拟合而成.由图看出, 动电渗透率测量结果很接近气测渗透率, 两者具有很好的相关性, 这说明动电测量可作为岩样渗透率测量的一种方法, 同时揭示了利用地层动电测井信号反演地层参数的可行性.
|
|
表 1 岩芯物性参数表 Table 1 Parameters of rocks |
|
|
表 2 岩芯的动电数据表 Table 2 The electrokinetcc results of rocks |
|
图 4 动电渗透率与气测渗透率的对比图 Fig. 4 The contrast diagram between electrokinetic permeability and gas permeability |
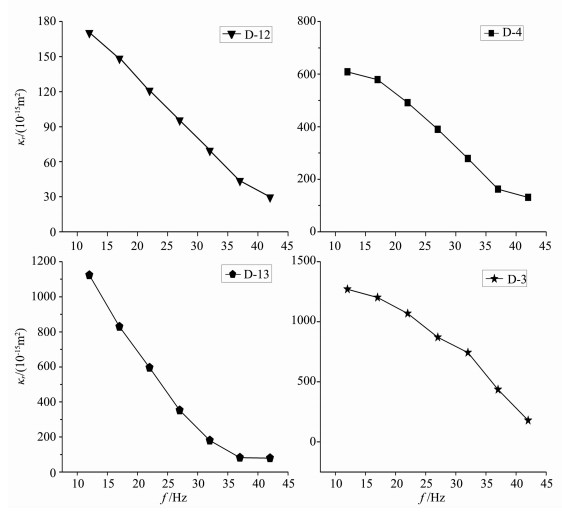
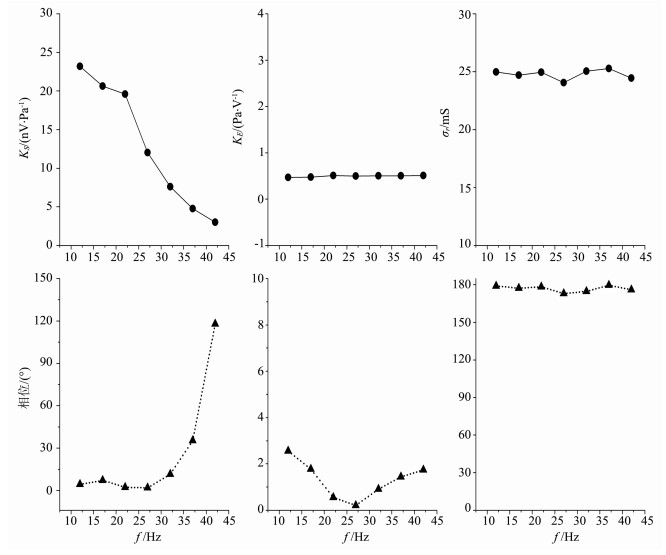
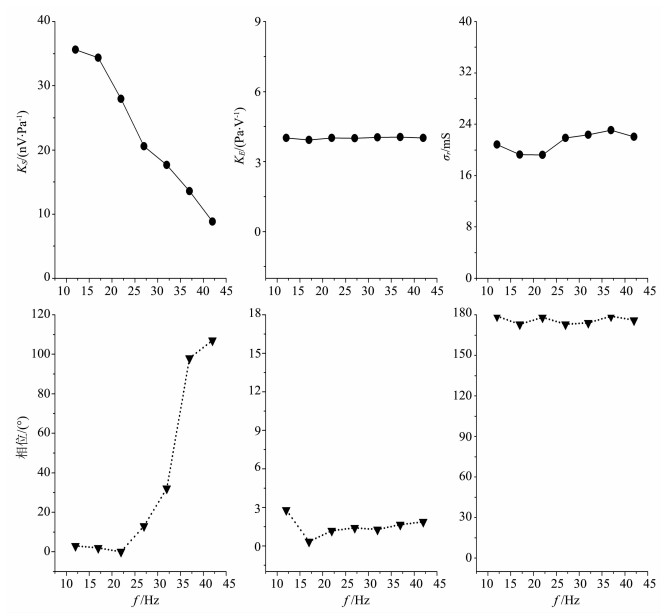
图 5是4块岩样动电渗透率的频率响应特性, 可以看出, 渗透率随频率降低逐渐增大, 这与Johnson[24]给出的动态渗透率变化趋势一致.图 6, 图 7分别是D-2、D-12岩芯动电参数的幅度和相位随频率变化的情况.其中KS的幅度随频率降低而增大, 最后趋于稳定, 但相位却随频率降低而降低, 特别在频率小于22 Hz以后相位几乎为零, 这与文献[25]中KS的理论变化规律相吻合.KE, σr的幅度和相位随频率变化都不大, 电导率σr在测量频带内出现了常相位角现象[5].
|
图 5 动电渗透率的频率响应 Fig. 5 The frequency response of electrokinetic permeability |
|
图 6 岩芯D-2动电参数的频率响应 Fig. 6 The frequency response of electrokinetic parameters of rock D-2 |
|
图 7 岩芯D-12动电参数的频率响应 Fig. 7 The frequency response of electrokinetic parameters of rock D-12 |
本文阐明了利用动电耦合效应测量岩芯渗透率的原理, 介绍了岩芯渗透率实验室测量系统的构成, 详细说明了采用锁相放大技术, 进行流动电势和电渗实验, 获得岩芯渗透率的过程.对于中、高渗透率岩样, 测量得出的动电渗透率与常规气测渗透率差异较小, 这验证了实验室中利用动电效应测量岩芯渗透率的可行性, 为实现井下测量地层渗透率奠定了基础.动电实验还可由(3)和(4)两式获得地层动电耦合系数L, 这对天然地震诱导电磁场特性的定量分析和研究有重要参考价值.
动电实验的关键在于采用了交流锁相放大技术.实验中使用的锁相放大器对电压和电流的测量精度可达纳伏级和帕安级, 这使得在较小的激励作用下便可获得计算岩芯渗透率所需的实验参数, 从而避免电极极化和较大的压力梯度对岩芯的破坏, 减小了实验误差, 同时保证了实验的可重复性.
实验使用NaCl溶液的浓度为0.05 mol/L, 若从仅为了获得更好的动电测量数据角度考虑, NaCl溶液的浓度可以取得更低些, 因为浓度越低, 双电层效应越明显, 动电耦合信号越强, 有利于实验参数的测量.但从声(动)电测井角度分析, 应研究不同矿化度、pH值及饱和度情况下的响应, 分析这些因素对动电测量的影响, 以满足处理、解释测井数据的需要, 为利用动电信号准确评价油气储层提供依据.这将是我们今后工作的重点.
另外, 动电渗透率测量系统也有待进一步改进.如(1)在夹持器设计方面, 能否更方便岩样的装、卸. (2)对于电子设备方面则需要调研一些具有更高性能的替代仪器, 特别是更高灵敏度的差压传感器.
| [1] | Kozeny J. Uber kapillare leitung des wassers im boden. Sitzungsber Akad Wiss Wien. , 1927, 136: 271-306. |
| [2] | 肖立志. 核磁共振成像测井与岩石核磁共振及其应用. 北京: 科学出版社, 1998 . Xiao L Z. Magnetic Resonance Imaging Logging and Rock's Magnetic Resonance and Its Application (in Chinese). Beijing: Science Press, 1998 . |
| [3] | Tang X M, Cheng C H. Fast inversion of formation permeability from Stoneley wave logs using a simplified Boit-Rosenbaum model. Geophysics , 1996, 61: 639-645. DOI:10.1190/1.1443993 |
| [4] | 李舟波. 地球物理测井数据处理与综合解释. 长春: 吉林大学出版社, 2003 . Li Z B. Processing and Synthesis Interpretation of Geophysics well Logging Data (in Chinese). Changchun: Jilin University Press, 2003 . |
| [5] | Pengra D B, Li S X, Wong P Z. Determination of rock properties by low-frequency AC electrokinetics. J.Geophys.Res. , 1999, 104: 29485-29508. DOI:10.1029/1999JB900277 |
| [6] | Jiang Y G, Shan F K, Zhou L W. A method for measuring electrokinetic coefficients of porous media and its potential application in hydrocarbon exploration. Geophys.Res.Lett. , 1998, 25: 1581-1584. DOI:10.1029/98GL01102 |
| [7] | Pride S R. Governing equations for the coupled electromagnetics and acoustics of porous media. Phys. Rev. B. , 1994, 50: 15678-15696. DOI:10.1103/PhysRevB.50.15678 |
| [8] | Zhu Z, Haartsen M W, Toks z M N. Experimental studies of electrokinetic conversions in fluid-saturated borehole models. Geophysics , 1999, 64: 1349-1356. DOI:10.1190/1.1444639 |
| [9] | 胡恒山, 王克协. 井孔周围轴对称声电耦合波:理论(I). 测井技术 , 1999, 23(6): 427–432. Hu H S, Wang K X. Coupled acoustic and electromagnetic waves around a borehole embedded in a porous formation:Theory (I). Well Logging Technology (in Chinese) , 1999, 23(6): 427-432. |
| [10] | 胡恒山, 王克协. 井孔周围轴对称声电耦合波:(Ⅱ)声电效应测井数值模拟. 测井技术 , 2000, 24(1): 3–13. Hu H S, Wang K X. Coupled acoustic and electromagnetic waves around a borehole embedded in a porous formation:Numerical simulation of acoustically induced fields (Ⅱ). Well Logging Technology (in Chinese) , 2000, 24(1): 3-13. |
| [11] | Mikhailov O V, Queen J, Toks z M N. Using borehole electroseismic measurements to detect and characterize fractured (permeable) zones. Geophysics , 2000, 65: 1098-1112. DOI:10.1190/1.1444803 |
| [12] | 胡恒山, 李长文, 王克协, 等. 声电效应测井模型实验研究. 测井技术 , 2001, 25(2): 89–95. Hu H S, Li C W, Wang K X, et al. Experimental study on coupled acoustic and electromagnetic waves in model wells. Well Logging Technology (in Chinese) , 2001, 25(2): 89-95. |
| [13] | 刘洪, 李幼铭. 对利用震电效应勘探油气水的几点看法. 石油物探 , 1994, 33(2): 94–101. Liu H, Li Y M. Comments on exploring oil, gas and water using seismoelectric effects. Geophysical Prospecting for Petroleum (in Chinese) , 1994, 33(2): 94-101. |
| [14] | 石昆法. 震电效应原理和初步实验结果. 地球物理学报 , 2001, 44(5): 720–728. Shi K F. Seismo-electric effect theory and preliminary experimental results. Chinese J. Geophys. (in Chinese) , 2001, 44(5): 720-728. |
| [15] | 陈本池, 牟永光, 狄帮让. 井中震电勘探模型实验研究. 石油物探 , 2003, 42(1): 35–38. Chen B C, Mu Y G, Di B R. Seismoelectric measurements in a borehole model. Geophysical Prospecting for Petroleum (in Chinese) , 2003, 42(1): 35-38. |
| [16] | 胡恒山, 刘家琦, 王洪滨, 等. 基于简化的Pride理论声电效应测井响应. 地球物理学报 , 2003, 46(2): 259–264. Hu H S, Liu J Q, Wang H B, et al. Simulation of acousto-electric well logging based on simplified Pride equations. Chinese J. Geophys. (in Chinese) , 2003, 46(2): 259-264. |
| [17] | 崔志文. 多孔介质声学模型与多极源声电效应测井和多极随钻声测井的理论与数值研究. 长春: 吉林大学, 2004 . Cui Z W. Theoretical and numerical study of modified Biot's models, acoustoelectric well logging and acoustic logging while drilling excited by multipole acoustic sources (in Chinese). Changchun: Jilin University, 2004 . |
| [18] | 关威, 胡恒山, 储昭坦. 声诱导电磁场的赫兹矢量表示与多极声电测井模拟. 物理学报 , 2006, 55(1): 267–274. Guan W, Hu H S, Chu Z T. Formulation of the acoustically-induced electromagnetic field in a porous formation in terms of Hertz vectors and simulation of the borehole electromagnetic field excited by an acoustic multipole source. Acta Physica Sinica (in Chinese) , 2006, 55(1): 267-274. |
| [19] | Scheidegger A E. The Physics of Flow Through Porous Media. New York: MacMillan, 1960 . |
| [20] | 高永新, 胡恒山. 水平分层孔隙介质中点源激发的震电波场数值模拟及分析. 地球物理学报 , 2009, 52(8): 2093–2104. Gao Y X, Hu H S. Numerical simulation and analysis of seismoelectromagnetic wave field excited by a point source in layered porous media. Chinese J. Geophys. (in Chinese) , 2009, 52(8): 2093-2104. |
| [21] | Morgan F D, Williams E R, Madden T R. Streaming potential of westerly granite with applications. J. Geophys. Res. , 1989, 94: 12449-12461. DOI:10.1029/JB094iB09p12449 |
| [22] | Korpi G K, DeBruyn P L. Measurements of streaming potentials. J.Colloid Interface Sci. , 1971, 40: 263. |
| [23] | 高晋占. 微弱信号检测. 北京: 清华大学出版社, 2004 . Gao J Z. Detection of Weak Signals (in Chinese). Beijing: Tsinghua University Press, 2004 . |
| [24] | Johnson D L, Koplik J, Dashen R. Theory of dynamic permeability and tortuosity in fluid-saturated porous media. J.Fluid Mech. , 1987, 176: 379-402. DOI:10.1017/S0022112087000727 |
| [25] | Philip M R, Morgan F D, Lesmes D P, et al. Frequency-dependent streaming potentials. J.Colloid Interface Sci. , 2001, 234: 194-203. DOI:10.1006/jcis.2000.7294 |
 2010, Vol. 53
2010, Vol. 53