大地电磁(MT)实测资料的一维(1-D)或二维(2-D)解释虽相对简单, 但实际情况中很少表现为理想2-D情况, 即不能用传统的Swift旋转法将坐标轴旋转到使阻抗张量的对角元素确切为零的方向[1].因此消除近地表 3-D非均匀体引起的曲线畸变, 然后作常规的正反演解释, 仍是当前最流行而又实际的研究途径[2].
近年来发展起来的张量分解法将观测阻抗张量分解为畸变矩阵和未受畸变的区域阻抗张量, 使MT畸变研究取得了突破性进展.国内赵国泽等[3]利用Bahr[4, 5]分解方法确定构造走向和偏离度; 晋光文等[6]尝试应用了由Yee等提出的正则分解方法; 魏胜等[7]对由Chave等[8]提出的全张量分解进行了研究; 而由Groom等[9~13]提出的处理近地表 3-D非均匀体引起的电场电流畸变的张量分解法, 假设3-D局部异常体覆盖在区域2-D之上(简记为3-D/2-D), 将观测阻抗张量分解为畸变张量和区域2-D阻抗张量, 从而恢复未畸变的区域阻抗, 是目前最为广泛应用的一种张量分解法, 称为GB分解法.它相比于Bahr分解更加简便易行, 相比于正则分解等数学分解方法具备更加直观的物理意义[14].
国内近年来对GB分解的研究中, 王书明[15]对GB分解做了适当变换, 尝试运用改进的广义逆法进行求解, 但未涉及实际资料的应用; 杨长福等[1, 2]讨论了单频点GB分解的合理性和条件, 使用视电阻率和相位代换GB分解定义式中的阻抗, 同时使用视电阻率和相位构建目标函数, 采用局部最小二乘算法进行了单频点GB分解, 在一定程度上改善了分解的稳定性; 胡玉平等[16, 17]利用遗传算法对GB分解进行了适当改进, 并探讨了畸变因子的影响, 但由于求解的方程组是欠定的, 无先验条件下很难求解.
以上研究当中包含的主要问题是: (1)单纯使用局部优化算法直接求解GB分解定义式, 由于初始值选取不当会导致求解过程不稳定; (2)单纯使用全局优化算法直接求解GB分解定义式, 速度慢, 一般获得最优解很难, 效率不如局部优化算法; (3)由于实测数据包含噪音和实际地质构造无法完全符合GB分解的模型假设而使GB分解难以稳定地进行.
为了解决以上问题, 使张量分解快速稳定地进行并较少地受分解条件限制, 本文采用混合优化算法对GB分解法进行改进, 通过模型试验验证, 形成改进的单频点GB分解方法, 最后应用于实测资料的张量分解, 并进行综合的分析.
2 方法原理 2.1 GB张量分解法Groom和Baily [9, 10]在3-D/2-D结构假设下, 将观测阻抗张量Z分解为

|
(1) |
其中, C为与频率无关的局部畸变矩阵, C=gTSA, g为标量, R为单位旋转矩阵, RT为R的转置, T为扭变矩阵, S为剪切矩阵, A为分裂张量, Z2-D为区域真实的2-D阻抗张量, 它们分别为

|
其中θ为走向角, t为扭变(twist)因子, e为剪切(shear)因子, s为分裂比例因子.g和A在数学上有非惟一确定的困难[1], 需要通过静校正的方法确定, 故并入Z2-D中, 而改用Z2表示gAZ2-D, 这样Z就可写成: Z=RTSZ2RT, 该式有7个未知数, 它们是Z2中TE和TM极化波波阻抗的实部和虚部以及θ、e和t, 于是(1)式可写为
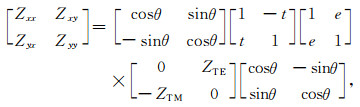
|
(2) |
其中, Zxx、Zxy、Zyx和Zyy分别为测量轴上观测阻抗张量元素.由(2)式左右两端阻抗张量对应元素实部和虚部相等, 便得到需求解的一个8×7的非线性超定方程组.
前人研究表明[1], 对各频点分别进行不约束分解, 即对单个频点进行张量分解将使分解条件不受限制, 并使方程和未知数的个数大大减少, 求解的稳定性和可实现性大大提高.
2.2 改进的思路及实现过程下面介绍如何利用混合优化算法求解8×7的非线性超定方程组, 从而实现单频点GB张量分解.
求解(2)式的关键是如何确定未知量的初值, 本文先使用模拟退火全局优化算法确定近似全局最优解空间, 作为局部优化算法(采用Matlab内置的非线性最小二乘函数)的初始值再行求解, 即可快速准确地得到全局最优解.因此, 要实现GB分解就是要在一定的搜索范围中, 尽量准确地确定局部优化算法的初始值.
一般来说, θ的搜索范围为-90~+90°之间, 经验表明, 经Swift旋转后的阻抗张量ZS为区域构造阻抗张量Z2-D与局部畸变张量C的综合贡献[18, 19], 即ZS=CZ2-D, 根据这个思路, 可由传统的Swift旋转法确定θ的初始值; 假设畸变前后的阻抗不会发生太大偏离, 则阻抗元素实部和虚部Real (ZTM)、Imag (ZTM)、Real (ZTE)、Imag (ZTE)的搜索范围可以由观测阻抗对应元素的实部和虚部值得到, 相应的初值即可取为观测阻抗值; 大量观测资料分解结果表明[1, 2, 9, 10, 12, 14, 20], 对于一般的地质构造来说, t值集中在-1~+1之间, 类似地, e在-1~+1之间才有意义, 但若无先验信息, 并无经验方法可得到其可靠初值, 则只能通过全局优化算法确定它们的初始值(即近似全局最优解).
具体来说, 对GB分解定义式(2)中各畸变矩阵进行求逆变换, 得

|
(3) |
由(3)式左端得到的2×2矩阵的主对角元素应为0, 则得到一个4×2的超定方程组, 可通过建立拟合差目标函数来评估真实值对计算值的偏离.设上式左端得到一个2×2矩阵D, 则对应的拟合差目标函数为
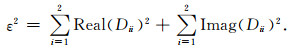
|
(4) |
使用模拟退火全局算法对其进行求解, 由于全局优化算法几乎不受初始值影响, 此时t和e的初始值取[-1, 1]之间的服从均匀分布的随机数, 即可获得t和e的解, 也即下一步局部算法求解的初值.
确定了局部优化算法所有待求参数的初始值, 就可通过视电阻率和相位所构建的拟合差目标函数(5)式进行局部寻优求解t、e、θ和区域阻抗的最终解:
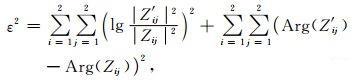
|
(5) |
其中Zij和Z′ij分别表示观测张量元素和计算张量元素, Arg为阻抗相位辐角.
综上, 改进后的单频点GB分解的整个流程如下: Swift旋转确定θ局部算法初始值→全局算法确定t、e的局部算法初始值→局部算法求解t、e、θ和区域阻抗.
单频点张量分解虽然对分解条件不作要求, 而且求解稳定, 每次分解时计算量较小, 但一个频点须作一次分解, 却很麻烦, 这是单频点张量分解的缺点[1].
3 模型试验和实例分析 3.1 单频点数据3-D单频点数据利用了Gary等[20]对北美中央平原2-D模型人为加入畸变获得的数据.各畸变参数的真值为arctant=-2.1°, arctane=24.95°, θ=0°
实际畸变阻抗为

|
依本文方法得到结果为arctant=-2.07°, arctane=24.97°, θ=0.07°,
计算畸变阻抗为
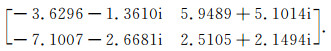
|
本文得到的结果已非常接近真值, 计算阻抗与实际阻抗的拟合程度也非常好, 其中全局优化算法的目标函数值为0.0021, 局部优化算法的目标函数值为2.4813×10-7.
文献[21]使用了基于共轭梯度的局部优化算法, 同样对其进行过试算(计算结果: arctant=-1.66°, arctane=26.59°, θ=0.69°), 而本文的混合优化算法利用全局优化算法不依赖于初值选取这一特性, 体现了更高的求解精度.
3.2 局部、全局和混合优化算法稳定性比较下面对不同算法的稳定性进行比较, 每种算法对上述单频点数据各计算50次, 每次取[-1, 1]之间的服从均匀分布的随机数作为t和e的初始值, 其他参数与前文相同, 所得结果如图 1, 其中横轴N为计算次数.可以看出: (1)单纯使用局部算法求解8×7方程组, 不同的初始值得到不同的结果(图 1 (a~c)), 说明结果不稳定, 需要用全局算法确定t和e的局部算法初始值.(2)单纯使用全局算法求解, 无论是求解8×7方程组还是先求解4×2方程组确定t和e的初值再求解8×7方程组, 结果也都不稳定(图 1(d~i)), 说明全局算法在未知数较多时易出现不稳定, 不适宜求解多元极值或弱局部极小等病态反问题.(3)本文的混合优化算法则使两种算法扬长避短, 相互结合, 结果稳定(图 1(j~l)).
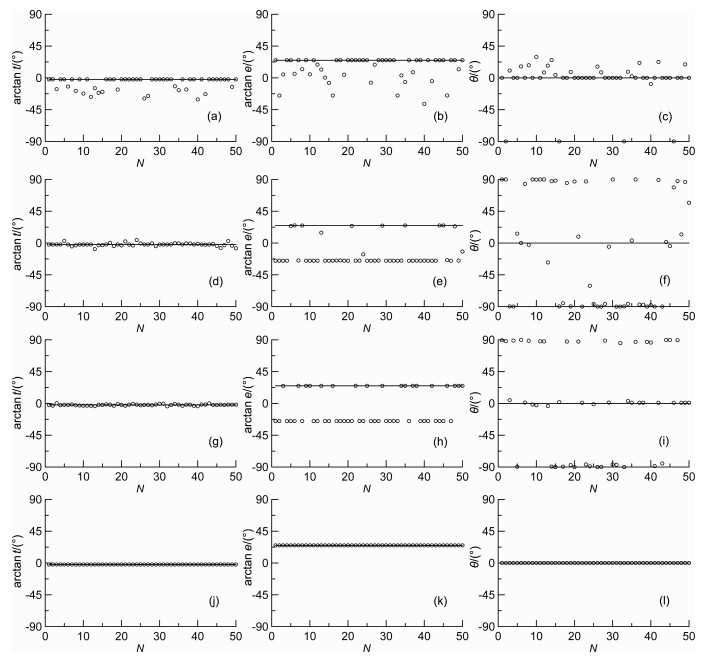
|
图 1 单频点数据的算法稳定性比较结果 圆圈为计算的arctant、arctane、θ值, 实线为理论值; (a)~(c)使用局部算法求解8×7方程组得到的结果; (d)~(f)使用全局算法求解8×7方程组得到的结果; (g)~(i)使用全局算法先求解4×2方程组确定t和e的初值再求解8×7方程组得到的结果; (j)~(l)使用本文的混合优化算法进行求解得到的结果. Fig. 1 Algorithm stability comparison of single frequency point Circles are calculated distortion parameter values, and solid lines are theoretical values; (a)~(c) Result of distortion parameters solving 8×7 equations by local optimal algorithm; (d)~(f) Result of distortion parameters solving 8×7 equations by global optimal algorithm; (g)~(i) Result of distortion parameters solving 8×7 equations after solving 4×2 equations by global optimal algorithm; (j)~(1) Result of distortion parameters of method in this paper. |
本文所采用的3-D模型数据来自于美国Utah大学的CEMI.此模型是一个局部构造为出露地表的3-D电性不均匀体、区域构造为1-D的3-D/1-D模型(如图 2).3-D电性不均匀体底界深度为400m, 1-D区域构造为三层水平介质中的A型模型, 与文献[22]中的模型类似.
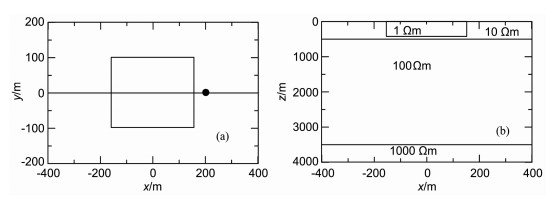
|
图 2 3-D/1-D模型示意图 (a)平面俯视图(实线为测线,圆点为测点,矩形区域为异常体范围);b)沿测线剖面图. Fig. 2 3-D/1-D model (a) Plan view (The solid line is the surveyed line and the dot is the surveyed point. The rectangle region is the anomalous body); (b) Cross-section along surveyed line. |
图 3中给出了图 2中测点处的3-D/1-D模型的视电阻率和相位曲线(图 3a、3d中的圆圈和圆点), 同时给出了1-D区域构造的视电阻率和相位曲线(图 3a、3b、3d、3e中的虚线).可看出, 在中低频段视电阻率曲线发生了平移, 相位曲线重合在一起.这说明在中、低频段以由电流型电场畸变引起的静位移为主; 在高频段, ρxy和ρyx之间以及它们与1-D曲线之间均不平行, 并且相位曲线形态也发生了变化, 所以这时仅对视电阻率曲线平移来校正静位移是无法得到合理的结果的, 为此我们采用本文的张量分解法来进行畸变校正.
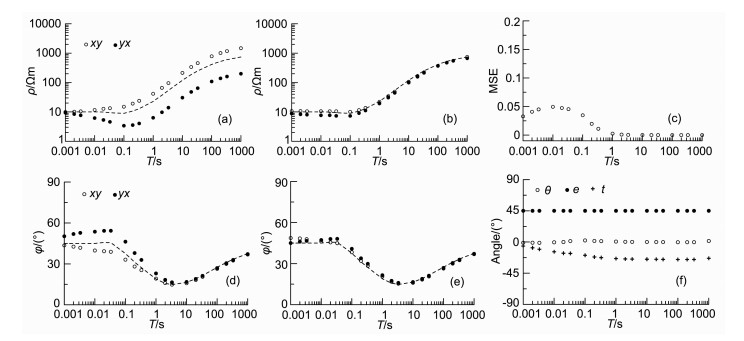
|
图 3 3-D/1-D模型分解结果 (a)~(b)本文方法视电阻率分解前后结果;(c)均方差目标函数曲线;(d)~(e)本文方法相位分解前后结果;(f)本文方法畸变参数分解结果. Fig. 3 Decomposition result of 3-D/1-D model (a)~(b) Result of apparent resistivity before and after decomposition; (c) Mean square error (MSE) curve; (d)~(e) Result of phase before and after decomposition; (f) Result of distortion parameters. |
可以看出, 校正后的视电阻率和相位曲线的形态在高频段已大大改善.从拟合误差曲线也可以看出, 计算的精度是满足计算要求的, 各频点拟合误差均小于0.05.
3.4 实例分析由于实测数据包含噪音, 再加上实际地质构造无法完全符合GB分解的模型假设, 会导致求解结果很不稳定.原因在于包含噪音的阻抗已不能像理想模型那样作为待求阻抗的初始值.此时, 可由GB分解定义式(2), 在确定t、e、θ的局部算法初始值后, 通过矩阵求逆得到区域阻抗的局部算法初始值, 再行求解.值得补充的一点是, 矩阵求逆时, 如果其病态性很严重(e接近于1), 得到的逆将会很不稳定, 则可依Lanczos的奇异值分解理论去掉小特征值, 求得其广义逆[15].
采用本文改进后的单频点GB分解法对下扬子菱塘桥地区实测资料进行了分解, 仅以其中的LTQ-EMAP08-8线208测点为例来说明张量分解结果(图 4).该测点位于目标构造附近, 但又邻近油田开采区和渔业养殖区之间, 其畸变校正结果在数据处理解释中很有代表性.

|
图 4 实测测点分解结果 (a)观测视电阻率曲线; (b) Swift旋转得到的视电阻率曲线; (c)本文方法得到的视电阻率曲线; (d)观测相位曲线; (e) Swift旋转得到的相位曲线; (f)本文方法得到的相位曲线; (g)本文方法得到的畸变参数. Fig. 4 Result of field surveyed point (a) Observed apparent resistivity; (b) Apparent resistivity after Switt rotation; (c) Apparent resistivity after decomposition; (d) Observed phase; (e) Phase after Switt rotation; (f) Phase after decomposition; (g) Distortion parameters. |
从分解前后结果对比可以看出, 改进后的GB分解对消除近地表 3-D电性不均匀体造成的畸变影响效果显著, 分解后的视电阻率和相位曲线较光滑连续、不失真, 非常便于下一步的圆滑、模式识别、静校正等资料处理工作, 对分析测区地下电性结构的分布特征和变化特点以及下一步定量反演和解释都打下了较好的基础.
4 结论和讨论本文在前人研究的基础上, 开发了改进的单频点GB分解方法.首先采用模拟退火全局优化算法, 通过对GB分解定义式的变换, 利用区域阻抗主对角元素为0这一条件, 求解获得t、e.由于只需要解包含t和e的4×2的非线性超定方程组, 使求解参数和计算量大大减少, 减少了其他参数的不稳定影响, 并提高了运算速度, 充分利用了GB分解定义式提供的阻抗信息, 同时使求解过程的稳定性大大提高.然后结合Swift旋转确定θ的初始值, 通过矩阵求逆得到所要求的区域阻抗的初值, 结合局部优化算法对8×7的非线性超定方程组进行求解, 获得稳定正确的最终解.本文方法初步解决了由于实测数据包含噪音和实际地质构造无法完全符合GB分解的模型的假设所造成的求解结果不稳定的问题.
如何利用先验地质信息获得各参数更加可靠的初始值, 而非单纯依靠数学方法, 使其更加直观真实, 是未来值得研究的一个问题.
| [1] | 杨长福, 林长佑, 徐世浙. 大地电磁GB张量分解法的改进. 地球物理学报 , 2002, 45(Suppl.): 356–364. Yang C F, Lin C Y, Xu S Z. The improvement of the Groom-Baily's tensor decomposition in magnetotellurics. Chinese J. Geophys. (in Chinese) , 2002, 45(Suppl.): 356-364. |
| [2] | 杨长福, 林长佑. 用大地电磁法研究构造走向及维性特征. 西北地震学报 , 2002, 24(1): 65–71. Yang C F, Lin C Y. The study on structural strike and dimensional character using magnetotelluric method. Northwestern Seismological Journal (in Chinese) , 2002, 24(1): 65-71. |
| [3] | 赵国泽, 汤吉, 刘铁胜, 等. 山西阳高-河北容城剖面大地电磁资料的初步解释--阻抗张量分解技术及其应用. 地震地质 , 1996, 18(1): 66–74. Zhao G Z, Tang J, Liu T S, et al. Preliminary interpretation of MT data along profile from Yanggao to Rongcheng:application of decomposition of MT impedance tensor. Seismology and Geology (in Chinese) , 1996, 18(1): 66-74. |
| [4] | Bahr K. Geological noise in magnetotelluric data:a classification of distortion types. Phys.Earth Planet.Inter. , 1991, 66: 24-38. DOI:10.1016/0031-9201(91)90101-M |
| [5] | Bahr K. Interpretation of the magnetotelluric impedance tensor:region induction and local telluric distortion. J.Geophys. , 1987, 62: 119-127. |
| [6] | 晋光文, 孙洁, 王继军. 大地电磁(MT)阻抗张量的正则分解及其初步应用. 地震地质 , 1998, 20(3): 243–249. Jin G W, Sun J, Wang J J. Canonical decomposition of the magnetotelluric (MT) impedance tensor and its preliminary application. Seismology and Geology (in Chinese) , 1998, 20(3): 243-249. |
| [7] | 魏胜, 王家映, 罗志琼. 全MT张量阻抗分解及其应用.见:应用地球物理学进展. 武汉: 中国地质大学出版社, 1998 : 38 -45. Wei S, Wang J Y, Luo Z Q. Magnetotelluric (MT) impedance full tensor decomposition and its application.In:Progress in Applied Geophysics (in Chinese). Wuhan: China University of Geosciences Publishing House, 1998 : 38 -45. |
| [8] | Chave A D, Smith J T. On electric and magnetic galvanic distortion tensor decomposition. J. Geophys. Res. , 1994, 99(B3): 4669-4682. DOI:10.1029/93JB03368 |
| [9] | Groom R W, Bailey R C. Decomposition of magnetotelluric impedance tensors in the presence of local three-dimensional galvanic distortion. J. Geophys. Res. , 1989, 94: 1913-1925. DOI:10.1029/JB094iB02p01913 |
| [10] | Groom R W, Bailay R C. Analytic investigations of the effects of near surface three-dimensional galvanic scatters on MT tensor decompositions. Geophysics , 1991, 56: 496-518. DOI:10.1190/1.1443066 |
| [11] | Groom R W, Bahr K. Correction for near surface effects:Decomposition of the magnetotelluric impedance tensor and scaling corrections for regional resistivities:A tutorial. Surv. Geophys. , 1992, 13(1): 341-379. |
| [12] | Groom R W, Kurtz R D, Jones A G, et al. A quantitative methodology to extract regional magnetotelluric impedances and determine the dimension of the conductivity structure. Geophys.J.Int. , 1993, 115: 1095-1118. DOI:10.1111/gji.1993.115.issue-3 |
| [13] | Jones A G, Groom R W. Strike-angle determination from the magnetotelluric impedance tensor in the presence of noise and local distortion:rotate at your peril!. Geophys.J.Int. , 1993, 113: 524-534. DOI:10.1111/gji.1993.113.issue-2 |
| [14] | 晋光文, 孔祥儒. 大地电磁阻抗张量的畸变与分解. 北京: 地震出版社, 2006 : 216 -323. Jin G W, Kong X R. The Distortion and Decomposition of Magnetotelluric Impedance Tensor (in Chinese). Beijing: Seismological Press, 2006 : 216 -323. |
| [15] | 王书明. 表面局部三维大地电磁曲线畸变校正--MT畸变校正阻抗张量分解方法. 西北地震学报 , 1998, 20(4): 1–11. Wang S M. The correction of magnetotelluric curve distortion caused by surficial local three-dimension inhomogeneties:the impedance tensor decomposition technique for the correction of MT curves distortion. Northwestern Seismological Journal (in Chinese) , 1998, 20(4): 1-11. |
| [16] | 胡玉平. 大地电磁阻抗的地质噪声畸变研究及校正方法. 长沙: 中南大学, 2004 . Hu Y P. The study of magnetotelluric impedance geologic noise distortion and correction method (in Chinese). Changsha: Central South Univercity, 2004 . |
| [17] | 胡玉平, 鲍光淑, 贾继标. 基于畸变3个因子的MT畸变曲线改正方法与应用. 地质与勘探 , 2005, 41(6): 75–79. Hu Y P, Bao G S, Jia J B. A method to correct MT curve on 3 distortion factors and its application. Geology and Prospecting (in Chinese) , 2005, 41(6): 75-79. |
| [18] | 晋光文, 孙洁, 白登海, 等. 川西--藏东大地电磁资料的阻抗张量畸变分解. 地球物理学报 , 2003, 46(4): 547–552. Jin G W, Sun J, Bai D H, et al. Impedance tensor distortion decomposition of magnetotelluric data from West Sichuan-East Xizang. Chinese J. Geophys. (in Chinese) , 2003, 46(4): 547-552. |
| [19] | 王立凤, 晋光文, 孙洁, 等. 一种简单的大地电磁阻抗张量畸变分解方法. 西北地震学报 , 2001, 23(2): 172–180. Wang L F, Jin G W, Sun J, et al. A simple decomposition method of distortion in magnetotelluric impedance tensor. Northwestern Seismological Journal (in Chinese) , 2001, 23(2): 172-180. |
| [20] | Gary W McNeice, Alan G Jones. Mutisite mutifrequecy tensor decomposition of magnetotelluric data. Geophysics , 2001, 66(1): 158-173. DOI:10.1190/1.1444891 |
| [21] | 李艳青. 张量阻抗分解的实现及在藏南构造走向研究中的应用. 北京: 中国地质大学, 2008 . Li Y Q. Tensor impedence decomposition realization and applying in the studying of the south-Tibet structure strike (in Chinese). Beijing: China University of Geosciences, 2008 . |
| [22] | 高红伟, 张胜业. 阻抗张量分解进行大地电磁静校正的研究. 地质科技情报 , 1998, 17(1): 91–96. Gao H W, Zhang S Y. Study of correction for static shift:the decomposition of magnetotelluric impedance tensors. Geological Science and Technology Information (in Chinese) , 1998, 17(1): 91-96. |
 2010, Vol. 53
2010, Vol. 53


