核爆地震自动识别是监测《全面禁止核武器试验条约》执行状况的一个有效方法, 特征的提取与选择是实现自动识别的关键问题.经过五十多年的研究, 人们已经找到了大量有效特征对核爆和地震进行分类[1~3].这些特征既包括具有明显地球物理意义的特征, 也包括从数理统计和信号处理的角度提出的特征.经过大量的研究证实, 由于核爆地震模式识别的复杂性, 不存在一个百分之百有效的特征能够将核爆炸和天然地震分开, 因此, 必须将不同类型的特征组合起来进行识别.这就带来这样一个问题:到底该选择哪些特征进行组合才能达到最佳的识别率~虽然从理论上讲, 特征越多越能提供反映事物本质的信息, 但是, 从分类器的泛化性能来看, 并不是说特征越多分类效果越好.由于不同特征之间的关系是非常复杂的, 大量特征的不恰当组合反而会降低系统的性能.在有限样本的情况下(核爆地震识别的情况即是如此), 随着特征向量维数的增加, 学习问题的计算复杂度将呈指数增长, 即人们常说的"维数灾难"即使在分类器能够处理高维数据的情况下, 特征选择对于提高系统的性能也常常是必不可少的.目前针对核爆地震特征选择问题展开研究的文献还不多.文献[4]将序优化理论用于核爆地震的特征选择中, 发现序优化方法能够在没有任何先验知识的前提下减小搜索空间, 提高搜索效率.文献[5]将遗传算法用于搜索次优的核爆地震特征子集, 取得了一定效果.
所谓特征选择, 就是从一组特征中挑出一些最有效的特征构成特征子集, 以达到降低特征空间维数的目的.为此, 需要解决两个问题:一个是特征的评估标准; 另一个是特征搜索算法.前人在这两个方面已经做了大量工作[6].按照评估的标准不同, 特征选择方法基本可以分为两类:封装式和过滤式.封装式直接使用分类器的识别率作为评估标准, 因此, 可以得到较高的识别精度.但是, 该方法在特征选择过程中必须使用分类器对每一个搜索到的特征子集进行训练和测试, 需要耗费大量时间, 且分类器改变时, 特征需要重新进行选择, 推广性不好.过滤式中的评估标准是独立于后续的学习算法的, 这些评估标准习惯称为类别可分性判据.过滤式特征选择方法一般运行效率高, 不依赖于学习算法, 推广性较好, 但是, 分类精度不如封装式, 特别是当可分性判据选择不恰当时, 效果很差.
特征选择也可以看作是一个组合优化问题, 因此, 可以不用传统的搜索算法而利用解决优化问题的方法来处理这个问题.一些比较新的性能较好的优化算法有:遗传算法[7]、模拟退火算法[8]、蚁群优化算法[9]等.克隆选择算法[10]是模拟自然免疫系统功能的一种新的智能方法, 能够快速地收敛到全局最优解, 文献[11]将其用于特征选择, 通过与基于遗传算法特征选择的结果相比较, 发现在有限代数内, 该算法能收敛到更优的特征子集.该文采用过滤式特征选择方法, 选择类别可分性判据中的Bhattacharyya距离作为特征子集优劣的评估标准, 但是, Bhattacharyya距离涉及条件概率密度, 计算复杂, 特别是当样本较少时, 得到的概率密度与实际的概率密度偏差可能较大.与此相比, 基于类内类间距离(用类内类间离散度矩阵进行度量)的可分性判据由于计算方便、概念直观清楚, 在实际中获得了广泛应用.但是这类判据是直接从各类样本间的距离算出的, 没有考虑各类的概率分布, 不能确切表明各类交叠的情况, 因此, 与错误概率没有直接联系.特别是当类别内呈现多峰分布时, 该判据会失效.这里说的多峰分布是指同一类的样本其内部又形成若干子类, 从而导致样本的概率密度函数是多峰的.作为本文研究对象的核爆地震数据, 其多峰分布是由震源类型的多样性造成的.文献[11]只研究了不事先指定最优特征子集维数情况下的特征选择问题, 这固然避免了最优特征子集维数确定的问题, 但是, 有时我们需要将特征维数限制在一定范围之内或在确定了最优特征子集维数的情况下进行特征选择.此外, 文献[11]提出的特征选择算法中没有单独的记忆抗体, 这样在处理特征选择这种离散情况下的优化问题时有可能遗漏搜索过的最佳特征组合.
针对上述种种问题, 本文根据克隆选择的基本原理, 提出了一种过滤与封装相结合的特征提取方法.该方法融合了封装式与过滤式二者的优点, 能够在时间开销增加不是太多的情况下, 得到比过滤式特征选择方法更好的子集.通过设定单独的记忆抗体, 能够保证最终结果是搜索过的特征子集中的最佳子集, 并且能够处理事先指定和不指定特征子集维数两种情况下的特征选择问题, 使得特征选择具有更大的灵活性.在类别可分性判据方面, 本文引人了一种基于局部类内类间离散度矩阵的类别可分性判据, 较好地解决了核爆炸和天然地震样本的多峰分布问题.
2 克隆选择原理当生物体受到病原体人侵时, 免疫细胞会产生相应的抗体识别并清除病原体.De Castro和Von Zuben根据免疫系统工作的基本原理提出的克隆选择原理, 描述了免疫系统在受到抗原刺激时进行免疫应答的基本特征.其基本思想是:只有那些能够识别抗原的细胞才进行分裂增生, 而那些不能识别抗原的细胞不能进行分裂增生.被选择的细胞受制于亲和力成熟过程, 该过程改善其与抗原的亲和力.亲和力高的细胞被选择并保留下来, 亲和力低的细胞将被淘汰.
克隆选择算法最初是用来解决机器学习和模式识别问题的, 该算法经过简单修改后也适用于解决优化问题.用克隆选择算法实现函数优化(求函数最大值)的工作过程如下[10]:
(1)确定抗原Ag (待优化目标函数)和产生一组初始抗体Ab (初始候选解), 抗体规模为N.
(2)计算所有抗体与抗原的亲和力f.
(3)选择群体Ab中具有最高亲和力的n个最佳抗体组成一个新的集合Ab{n}.
(4)按照各个抗体与抗原的亲和力分别克隆所选的n个最佳抗体, 产生一个新的集合C:亲和力越大的抗体产生的克隆体的数量也越多.
(5)按照各个抗体与抗原的亲和力克隆群体C进人亲和力成熟过程, 最终产生成熟的克隆群体C*:亲和力越大的抗体变异概率越小.
(6)计算成熟的克隆群体C*的亲和力f*.
(7)从成熟的克隆群体C*中再次选择具有最高亲和力的n个最佳抗体, 将其亲和力值同C中的n个最佳抗体的亲和力值进行比较, 从这2n个抗体中选出n个最佳抗体代替(3)中的n个最佳抗体, 更新当前的群体Ab.
(8)用新抗体取代Ab中m个具有最低亲和力的抗体, 保持抗体的多样性.
以上8个步骤全部执行一次称为一代.
3 基于克隆选择原理的特征选择方法 3.1 特征选择过程中的几个关键问题既然特征选择的过程为一个寻优过程, 因此, 可以仿照克隆选择算法解决函数优化问题的基本原理, 设计出相应的特征选择方法.下面给出特征选择过程中关键步骤的实施方案和一些参数的设置.
(1)确定抗原Ag:分类器的识别率或类别可分性判据.文中涉及了两种准则, 一是k-近邻分类器的正确识别率, 二是一种基于类内类间离散度矩阵的类别可分性判据.其中基于类内类间离散度矩阵的类别可分性判据也有很多不同的定义方式, 文中采用如下的定义[12](后文中称其为J3准则):
其中Sb为类间离散度矩阵, Sw为类内离散度矩阵, tr代表矩阵的迹.本文针对类别内呈多峰分布的特征选择问题, 而J3准则在处理多峰分布的问题时效果不好.因此, 我们引人了一种局部化的J3准则, 该准则通过加权矩阵将类内类间离散度矩阵局部化, 从而能更有效地处理多峰问题1)局部J3准则的关键在于加权矩阵的选择, 本文选择的加权矩阵由(2)式给出,
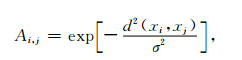
|
(2) |
其中σ为尺度参数, 其值为正, xi与xj分别代表原始特征空间的第i个和第j个样本.
1)有关不同形式的基于类内类间离散度矩阵的类别可分性判据的比较及局部J3准则的详细内容可参看:韩绍卿, 李夕海, 刘代志.基于局部类内类间离散度矩阵的类别可分性判据.http://www.paper.edu.cn/paper.php?serial_number=200910-479, 2009
(2)确定初始抗体群体Ab:随机产生N个(抗体规模)采用二进制编码的基因串, 其长度为特征向量的维数l编码为(a1, a2, …, al), 其中, 基因位ai, 为1表示相应的特征分量被选中, 为0表示相应的特征分量未被选中.
(3)将不同的抗体按照其与抗原的亲和力f的大小作降序排列, 选择前n个抗体组成一个新的集合Ab{n}, 并保持抗体的排序不变.
(4)对集合Ab{n}中的每个抗体进行克隆, 克隆体的排序沿用其父体的排序, 每个抗体的克隆规模按下式确定: Nc=round (N/i), (i=1, 2, …, n), 其中round (·)代表四舍五人, 得到克隆群体集合C, 在该过程中亲和力越高, 克隆规模越大.
(5)将C中的各个抗体进行变异, 对于其中排列次序号为i的抗体, 变异规则如下:随机选择i个基因位, 若该位为1, 将其变为0, 若该位为0, 将其变为1, 得到成熟的抗体C*亲和力越高的抗体变异概率越小.
(6)n和m可以根据需要设定不同的值, 本文采用的取值方式为: n=m=round (N/3), 即认为在求解过程中, 亲和力最高的前1/3抗体为最佳抗体, 亲和力最差的1/3抗体被随机产生的新抗体取代.
在特征选择过程中, 一些经典的搜索算法, 比如分支定界算法, 都需要事先给定子集维数, 然而, 最优特征子集维数的确定有时是比较困难的.上述(2)和(5)中抗体的产生和进行变异的基因位的选择都是完全随机的, 这种设置方法适用于事先无法确定最优特征子集维数的情况.若根据要求, 需要在指定维数(设为d)的情况下进行特征选择, 则采用如下的设置方法:
(2*)确定初始抗体群体Ab:随机产生N个(抗体规模)采用二进制编码的基因串, 其长度为特征向量的维数l, 该基因串有且仅有d个基因位为1, 编码为(a1, a2, …, al, ), 其中, 基因位ai, 为1表示相应的特征分量被选中, 为0表示相应的特征分量未被选中.
(5*)将C中的各个抗体进行变异, 对于其中排列次序号为i的抗体, 变异规则如下:在取值为1的d个基因位中, 随机选择i个基因位, 将其变为0, 在取值为0的基因位中, 随机选择i个基因位, 将其变为1, 得到成熟的抗体C*, 亲和力越高的抗体变异概率越小.
3.2 基于克隆选择原理的过滤与封装相结合的特征选择方法为了吸取封装式和过滤式两种特征选择方法的优点, 本文提出了一种将二者有效结合的方案.该算法的步骤如下:
(1)执行第2节中用克隆选择算法实现函数优化方法的步骤(1)~(8), 其中待优化的目标函数为局部J3准则;
(2)用分类器的正确识别率对(1)中得到的抗体进行评价.被评估的抗体可以是全部N个抗体, 也可以是其中的部分较好(相对于局部J3准则)的抗体, 比如n个最佳抗体;
(3)产生一个记忆抗体Abm, 储存(2)中产生的最佳抗体.该记忆抗体代表种群进化到目前为止所产生的正确识别率最高的特征子集.
以上3个步骤全部执行一次为一代.
该算法中关键步骤的实施方案和参数的设置同3.1节所述.若不预先指定特征子集维数, 执行3.1节中的(2)和(5), 否则执行(2*)和(5*).
在文献[10]中, 只有在解决机器学习和模式识别问题时才专门设定独立的记忆抗体, 在优化问题中整个种群的抗体都视为记忆抗体.我们设定一个单独的记忆抗体, 主要是基于三个方面的考虑:一是利用克隆选择原理实施的寻优过程是一个不断演化的过程, 只要终止条件不满足, 最优解就会处在不断变化的状态, 并且这种变化具有一定的盲目性; 二是特征选择问题是一个离散形式的优化问题, 它不同于连续条件下的优化问题, 即便是一个基因位发生变异, 最终的识别结果也有可能发生较大的变化(不同的特征对分类的贡献是不一样的, 特别是当对分类贡献较大的特征对应的基因位发生变异时, 这种情况最容易出现), 也就是说在离散情况下, 待优化的目标函数值有可能发生跳变; 三是与封装式或过滤式特征选择方法不同, 过滤与封装相结合的特征选择方法涉及两种对特征子集进行评估的准则.在进化过程中, 主导进化方向的是基于类内类间离散度矩阵的类别可分性判据, 即便是采用改进的计算准则, 很多情况下这种准则与我们最终在模式识别过程中采用的分类器准则也有相当的不一致性, 这就意味着根据类别可分性判据得出的较好(而非最好)的特征子集有可能恰好是识别率最高的特征子集.也就是说, 可分性判据较大的那些值而非最大值对应的特征子集才是最佳子集.这样, 通过设定单独的记忆抗体我们就尽可能保证最终得到的特征子集是所搜索过的子集中的最佳子集.需要指出的是, 通过上面分析的第一点和第二点可知, 即便是采用封装式的特征选择方法, 通过设定记忆抗体也会使效果有所提高.本文的实验结果也说明了这一点.
对于类别可分性判据, 除了要求其与误判概率(或误判概率的界限)有单调关系外, 还希望它对特征数目是单调不减的, 即加人新的特征后, 判据值不减[13].研究中发现, (1)式所示的类别可分性判据通常不满足对特征数目单调不减这一特性.很多情况下, 某一维特征的准则值是最大的.也就是说, 在特征选择前, 如果事先不指定最优子集的维数, 按照过滤式的特征选择方法, 最终获得的子集往往是一维的.而从识别率的角度看, 大多数情况下只选用某一个一维特征进行分类识别肯定不是最佳的.因此, 在选用(1)式所示的类别可分性判据作为评估准则时, 最好事先指定最佳特征子集的维数.但是, 很多情况下最佳子集的维数是很难确定的.当采用过滤与封装相结合的特征选择方法后, 由于设定了记忆抗体, 既可以先确定最佳子集的维数, 也可以不指定维数, 而按照优化目标由免疫系统自动获得最佳子集的维数.这样, 在处理特征选择问题时就有了更大的灵活性.
4 方法有效性验证下面通过标准数据库中的实测数据验证本文所提方法的有效性.研究对象为多峰分布情况下的特征选择问题.
4.1 实验数据和实验条件设置所选用的实验数据为UCI标准数据库中的玻璃识别数据库2).该数据库总共有214个样本, 每个样本提取了9维特征.所有样本可以细分为6个类别.如果按照识别对象是否为窗户玻璃来划分, 则是一个两类识别问题.窗户玻璃有三种不同的类型, 非窗户玻璃也有三种不同的类型, 因此该问题是一个多峰情况下的模式识别问题.克隆选择的过程是一个反复迭代、逐步更新的过程.原始特征为9维, 因此, 基因串长度l为9.由于原始特征空间维数较低, 因此, 迭代次数G和抗体规模N取值都较小.实验中根据不同的实验条件, G的取值为3或4, N设定为6.用正确识别率对所选特征子集的优劣进行评价时采用的分类器为近邻分类器, 正确识别率由10折交叉验证的方法得到.在将可分性判据局部化时, 尺度因子σ2取值为0.1.由于克隆选择过程本质上是一个随机搜索过程, 搜索过程有一定的随机性, 并且搜索起点的设置会对结果有一定的影响, 因此, 最终的识别率结果都是重复多次实验(本文采用20次)后得到的平均结果.
2) AsuncionA, Newman D J. UCI Machine Learning Repository [http://www.ics.uci.edu/~mlearn/MLRepository.html]. Irvine, C A: Universityof California, School of Information and Computer Science, 2007
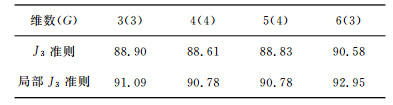
4.2 局部J3准则有效性验证该实验利用克隆选择原理, 采用过滤式特征选择方法进行特征选择, 特征评价标准分别为J3准则和局部J3准则, 得到最佳子集后用4.1节中的识别率计算方法验证每个子集的识别效果.实验结果见表 1.从表 1可以看出, 在所选择的不同维数下, 由局部J3准则得到的最优子集的正确识别率都要高于由J3准则得到的最优子集的正确识别率.这说明在多峰分布的情况下, 采用局部J3准则要好于J3准则.
|
|
表 1 两种准则条件下所得最优子集的平均正确识别率(%)括号中的数字代表迭代次数G Table 1 Average accuracy rates of the optimal subsets under different criterions (%) The numbers in the bracket denote G |
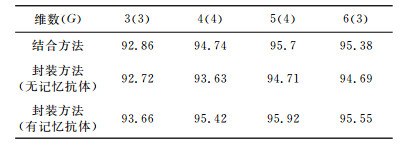
利用过滤与封装相结合的特征选择方法进行特征选择时, 由分类器正确识别率进行评估的抗体个数为抗体规模的一半.指定子集维数情况下的实验结果见表 2.作为比较, 表 2也给出了相同条件下封装特征选择方法的结果.可以看出, 过滤与封装相结合的特征选择方法识别效果甚至要好于无记忆抗体的封装式特征选择方法.在采用其他寻优算法比如分支定界算法时, 不会出现这种现象.这是因为分支定界这类算法在搜索过程中会记录下搜索到目前状态所产生的最佳特征组合, 而基于克隆选择原理的封装式特征选择方法中没有独立的记忆抗体来记录当前产生的最佳抗体, 在进化过程中, 上一代的最佳抗体必定发生变异, 变异后的抗体其亲和力有可能下降, 从而可能遗漏最佳特征组合.详细解释参见3.2节.为了说明解释的合理性, 仿照过滤与封装相结合的特征选择方法, 在封装方法中同样设定一个独立的记忆抗体, 在同以上相同的实验条件下进行了实验, 结果仍示于表 2中.与没有记忆抗体的封装方法相比, 在增加了记忆抗体后, 封装方法的识别性能有了较为明显的提高.对比分析表 2中不同实验条件下的识别结果可以看出, 即便是增加了记忆抗体后, 过滤与封装相结合的特征选择方法的效果与封装式特征选择方法的效果也是比较接近的, 特别是在特征子集维数为5和6时.
|
|
表 2 指定子集维数情况下, 过滤与封装相结合方法及封装方法的平均正确识别率(%)括号中的数字代表迭代次数G Table 2 Average accuracy rates of filter-wrapper and wrapper in the case of specified dimensionalities (%) The numbers in the bracket denote G |
如果不进行特征选择, 直接采用全部特征进行分类识别, 仍然采用相同的分类器和验证方法, 经过20次实验获得的平均正确识别率为94.89%.将采用全部特征的分类结果同上述经过特征选择后的分类结果对比, 可以看出, 在进行分类识别时, 并不是特征越多越好.通过选择合适的特征选择方法, 不仅可以降低特征空间的维数、减少计算量, 而且还有可能提高识别精度.
5 核爆地震特征选择实验结果及分析 5.1 实验数据和实验条件设置本文实验所用的数据分为两类, 一类是核爆炸产生的地震波数据, 另一类是天然地震所产生的地震波数据.其中核爆炸共有103个样本, 天然地震共有125个样本.两类样本都为短周期地震波记录, 样本的采样率为40 Hz.为了计算方便和方便对比, 对每个样本从地震波初至点开始截取1024个数据点, 在此基础上, 对每个样本提取12类、共43维的特征, 即:一阶相关、一阶谱相关、二阶相关、二阶谱相关、三阶相关、三阶谱相关、波形复杂度、谱比值、频率三次矩各1维, 短时谱3维, AR模型系数6维, 实倒谱25维.依次把这些特征编号为1, 至43.实验即是从这43维特征中选出最优特征.实验中种群规模N取10, 迭代次数G取20, 识别率计算方法同4.1节.
在UCI标准数据库中的玻璃识别数据库上进行特征选择实验时, 将可分性判据局部化时, 采用(2)式中的加权矩阵, 一旦选定就不再变化, 因此是一种全局的尺度因子.在进行核爆地震特征选择时, 为了能根据数据局部结构自动调节尺度因子, 我们进一步将尺度因子局部化, 其加权矩阵由(3)式给出[14]:
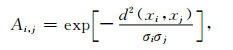
|
(3) |
(3)式中, 每一个数据点xi对应一个尺度因子σi.从xi"看到的"xi与xj之间的距离为d(xi, xj)/σi, 从xj"看到的"xi与xj之间的距离为d(xi, xj)/σj.σi可以通过学习xi的局部统计特性来确定, 本文选择如下形式的局部尺度因子[14]:
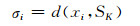
|
其中SK为xi的第K个近邻, 在本文中K取7.
5.2 过滤式核爆地震特征选择结果采用过滤式特征选择方法对核爆地震进行特征选择.实验分别采用J3准则和局部J3准则作为特征评价标准.由过滤式选择出最佳特征子集后, 再用识别率对两种情况下获得的最佳特征子集进行评价, 识别率计算方法同4.1节中的方法.两种情况下的实验结果如图 1所示.可以看出, 除了特征子集维数为3的情况之外, 采用局部J3准则获得的识别率在90%以上, 而采用J3准则获得的识别率都低于90%;不管特征子集维数取何值, 采用局部J3准则的识别效果都要好于采用J3准则的识别效果.

|
图 1 J3准则和局部J3准则特征选择后不同特征子集的识别率曲线局部 J3准则采用局部化的尺度因子. Fig. 1 The curves of accuracy rates of different subsets using J3 and local J3Localized scale parameters beingused in the local J3. |
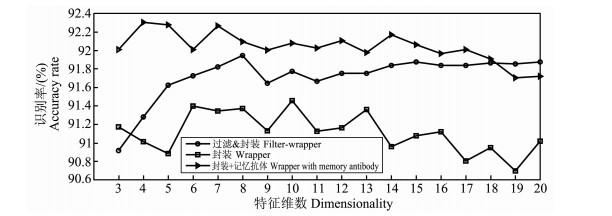
利用过滤与封装相结合的特征选择方法, 在核爆地震数据库上进行了特征选择实验.在事先指定特征子集维数情况下的实验结果示于图 2, 作为对比, 图中还给出了采用封装式特征选择方法的实验结果.可以看出, 采用封装式特征选择方法时, 是否设定独立的记忆抗体对特征选择效果有一定影响.若不设定独立的记忆抗体, 封装式特征选择方法效果不如过滤与封装相结合的特征选择方法; 设定独立的记忆抗体后, 在特征子集维数较低时, 封装式特征选择方法效果好于过滤与封装相结合的特征选择方法, 在特征子集维数较高时, 二者识别效果相当, 但结合式特征选择方法耗时明显低于封装式特征选择方法.
|
图 2 指定子集维数情况下特征选择后不同特征子集的识别率曲线 对于过滤 & 封装方法, 局部J3准则采用局部化的尺度因子. Fig. 2 The curves of accuracy rates of different subsets in the case of specified dimensionalities Localized scale parameters beingused in the local J3 for the Filter-wrapper method. |
若事先不指定特征子集维数, 由系统自动获得最优特征子集, 其结果(20次实验平均)见表 3.从识别率来看, 过滤与封装相结合的方法好于无记忆抗体情况下的封装方法, 与有记忆抗体情况下的封装方法相差很小.过滤与封装相结合的方法所获得的最优子集的平均维数大约为封装方法所获得的最优子集平均维数的一半, 并且搜索到最优子集所用时间还不到封装方法所用时间的1/5.
|
|
表 3 不指定子集维数情况下, 过滤与封装相结合方法及封装方法的实验结果 Table 3 Results of filter-wrapper and wrapper in the case of dimensionalities not specified |
如果不进行特征选择, 直接采用全部特征进行分类识别, 仍然采用相同的分类器和10折交叉验证的方法, 经过20次实验获得的平均正确识别率为89.91%, 该识别率低于特征选择后的识别率.本文提出的过滤与封装相结合的核爆地震特征选择方法, 在特征空间维数为8时达到最佳识别效果, 其正确识别率为91.95%, 比使用全部特征的识别率提高了2个百分点.可见, 在进行核爆地震识别时, 特征选择是非常重要的, 选择恰当的特征组合, 不但能有效降低特征维数, 从而有利于分类器的设计和训练, 而且还能提高识别精度.
6 讨论与结论在核爆地震模式识别中, 地震波信号的分布呈现多峰性.这是因为:对于天然地震来说, 其震源类型是多种多样的, 所接收到的地震波还受到震源周围的地质结构和传播路径的影响; 对于核爆炸来说, 造成多峰性的主要原因有:核装药的填埋方式及引爆方式, 当量的大小及爆炸点周围的地质结构和传播路径.传统的类别可分性判据, 如J3准则, 不能有效处理类别呈多峰分布的问题, 用其进行核爆地震特征选择, 效果自然不理想.本文提出将J3准则局部化的方法来解决这一问题.J3准则局部化的关键在于加权矩阵的选择, 可以定义不同形式的加权矩阵, 本文只研究了指数型加权矩阵, 且尺度参数的设置是在一定的范围内搜索获得的较好值, 因此, 所得结果不一定是最优结果.目前存在的问题是, 对于如何获得最佳的加权矩阵尚无普适性的理论方法, 因此, 有必要针对如何获得最优加权矩阵开展进一步研究.
在核爆地震自动识别中需要综合运用多种特征以保证识别的可靠性.最优的特征选择可以作为一个组合优化问题来处理.在引入局部化的类别可分性判据的基础上, 利用克隆选择算法能够快速收敛于全局最优解的特性, 本文提出了一种过滤与封装相结合的特征选择方法.该方法融合了封装式与过滤式二者的优点, 能够在计算量增加不多的情况下得到比过滤式更好的子集.该方法既可以事先确定最优特征子集的维数, 也可以不指定维数, 而按照优化目标由免疫系统自动获得最佳子集的维数, 能够更灵活地处理模式识别中的特征选择问题.从实验结果来看, 利用本文提出的特征选择方法, 不但有效降低了核爆地震分类过程中特征空间的维数, 而且使分类精度提高了2个百分点.
| [1] | 李夕海, 刘刚, 刘代志, 等. 基于最近邻支撑向量特征线融合算法的核爆地震识别. 地球物理学报 , 2009, 52(7): 1816–1824. Li X H, Liu G, Liu D Z, et al. Discrimination of nuclear explosions and earthquakes using the nearest support vector feature line fusion classification algorithm. Chinese J. Geophys. (in Chinese) , 2009, 52(7): 1816-1824. |
| [2] | 沈萍, 郑治真. 瞬态谱在地震与核爆识别中的应用. 地球物理学报 , 1999, 42(2): 231–240. Shen P, Zheng Z Z. Application of transient spectrum to discrimination of nuclear explosions and earthquakes. Chinese J. Geophys. (in Chinese) , 1999, 42(2): 231-240. |
| [3] | 杨选辉, 沈萍, 刘希强, 等. 地震与核爆识别的小波包方法. 地球物理学报 , 2005, 48(1): 148–156. Yang X H, Shen P, Liu X Q, et al. Application of method of spectral component ratio of wavelet-packets to discrimination between earthquakes and nuclear explosions. Chinese J. Geophys. (in Chinese) , 2005, 48(1): 148-156. |
| [4] | 李夕海, 刘代志, 张斌, 等. 序优化在核爆地震特征选择中的应用研究. 兵工学报 , 2005, 26(4): 496–499. Li X H, Liu D Z, Zhang B, et al. Feature selection of seismic pattern recognition of nuclear explosions based on ordinal optimization. Acta Armament Arii (in Chinese) , 2005, 26(4): 496-499. |
| [5] | Orlic N, Loncaric S. Earthquake-explosion discrimination using genetic algorithm-based boosting approach. Computers & Geosciences , 2010, 36(2): 179-185. |
| [6] | Dash M, Liu H. Feature selection for classification. Intelligent Data Analysis , 1997(1): 131-156. |
| [7] | Siedlecki W, Sklansky J. On automatic feature selection. International Journal of Pattern Recognition and Artificial Intelligence , 1988, 2(2): 197-220. DOI:10.1142/S0218001488000145 |
| [8] | Kirkpatrick S, Gelatt Jr C D, Vecchi M P. Optimization by simulated annealing. Science , 1983, 220: 671-680. DOI:10.1126/science.220.4598.671 |
| [9] | Gutjahr W J. A graph-based ant system and its convergence. Future Generation Computing Systems , 2000, 16: 873-888. DOI:10.1016/S0167-739X(00)00044-3 |
| [10] | De Castro L N, Von Zuben F J. Learning and optimization using the clonal selection principle. IEEE Trans on Evolutionary Computation , 2002, 6(3): 239-251. DOI:10.1109/TEVC.2002.1011539 |
| [11] | 张向荣, 焦李成. 基于免疫克隆选择算法的特征选择. 复旦大学学报(自然科学版) , 2004, 43(5): 926–929. Zhang X R, Jiao L C. Feature selection based on immune clonal selection algorithm. Journal of Fudan University (Natural Science) (in Chinese) , 2004, 43(5): 926-929. |
| [12] | 孙即详, 等. 现代模式识别. 长沙: 国防科技大学出版社, 2002 . Sun J X, et al. Modern Pattern Recognition (in Chinese). Changsha: National University of Defense Technology Press, 2002 . |
| [13] | 边肇祺, 张学工编著.模式识别(第二版).北京:清华大学出版社, 1999. Bian Z Q, Zhang X G. Pattern Recognition (2nd Edition) (in Chinese). Beijing:Tsinghua University Press, 1999 http://www.oalib.com/references/19342176 |
| [14] | Zelnik-Manor L, Perona P. Self-tuning spectral clustering. In:Saul L K, Weiss Y, Bottou L eds. Advances in Neural Information Processing Systems. Cambridge, MA:MIT Press, 2005, 17:1601~1608 |
 2010, Vol. 53
2010, Vol. 53