2. 浙江大学海洋科学与工程学系, 杭州 310058
2. Department of Ocean Science and Engineering, Zhejiang University, Hangzhou 310058, China
目前在大型河道中常采用单点式流速仪(机械式流速仪、电接式流速仪等)和声学多普勒流速剖面仪(Acoustic Doppler Current Profiler, 简称ADCP)进行测流[1, 2].但是这些常规测流方法只能观测一个点或一个剖面的流速.要得到河道中一个断面的平均流速和流量,就必须在某一断面布放很多流速仪或进行走航观测来实现.但是长江、钱塘江等大型河道是我国水路的交通枢纽,常规的测流方法经常受到船舶航行等的干扰,不能实现对流速、流量长期、连续的实时监测.
声传播会受到船体本身的阻隔,但声线可以从航行中船与船的间隙通过,部分声线还能从船舶下的水体通过.声传播不会完全受到船体本身的阻隔,基本能够实现对流速和流量长期、连续的实时监测[3].
河道的断面流量还可以根据水位仪测量河流的水位,通过与其他流量实测资料作经验回归得到流量的经验公式来推算流量[4].因水位流量关系受水力因素等的影响,并且随时间的推移而发生变化,往往在流量推算时引起较大的误差.另外,位于人海口附近的河道,其水位受潮位影响,使得河道中的流速会发生转向,同一个水位的值会对应两个相反流向的流速,无法根据水位的变化直接得到流速(流量),所以无法用水位仪来实现流量监测.
超声波的顺逆流传播时间差测流法已经广泛应用于工业生产以及明渠的流量监测中[5, 6].但要运用于大型河道中不仅需要解决仪器异地时钟同步的问题,还需克服环境噪声.在国外,传播时间差测流法已成功在海洋[7]以及河道[8]中进行测流.在国内,虽已成功地应用于海洋测流,但尚未有在大型河道中的应用先例[9].
本文针对以上这些问题,在钱塘江进行了双向声传播测流实验,实现了双向声传播对大型河道流速和流量的监测.
2 原理如图 1在河道两岸A和B设置两个站位,分别由A和B向对方发送声信号,并接收对方发来的信号.河道中声速(温度)的水平梯度远小于其垂直梯度,忽略声信号传播时声线水平方向的弯曲,A、B间的双方向传播时间τ1、τ2分别为:
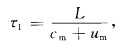
|
(1) |

|
(2) |

|
图 1 两个站位间双向声传播示意图 图中灰色的的平行四边形表示河道水面,黑圆柱体表示换能器,白色圆柱体表示携有GPS的双向声传播系统(CATS). Fig. 1 Sketch of the reciprocal sound transmission between two stations The shaded parallelogram represents the water surface of the river.The black and white cylinders indicate the transducers and CATS connected with GPS antenna, respectively. |
其中,cm和um分别是A、B间的平均声速和沿A-B方向的平均流速,L为站位间的距离.用式(1)和(2)通过简单的推导可得到um和cm:
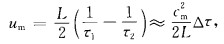
|
(3) |
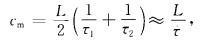
|
(4) |
其中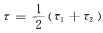

|
(5) |
由于τ>>δτ,△τ>>δ(△τ),上式第一项约为9.8×10-3,第二项约为9.7×10-7, 第三项约为6.7×10-4, 第一项的值远远大于后面两项,后两项忽略可得
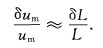
|
(6) |
假设两个站位间的距离L=3 km,一般GPS的位置误差30 m, 由式(6)得到δum=0.01um.当A-B间的平均流速um=l m/s时,对应的误差值为δum=0.01 m/s.即在实现两站位间GPS时钟同步的条件下,由距离误差导致平均流速的观测误差极小,能保证um测量的高精度.
3 实验地点与方法双方向声传播实验在钱塘江杭州段进行.因为天体引潮力以及钱塘江喇叭状特殊地形的原因,在大潮期间会形成雄伟壮观的钱塘江涌潮.实验地点离杭州湾约90 km,可用目测判断钱塘江涌潮的到来.
双方向声传播实验分两个阶段:第一阶段从2009年4月8日到9日,第二阶段从2009年5月8日到10日.选择了W和E两个站位,W站位于钱塘江闸口水文站,E站位于复兴大桥南端的桥墩上,两个站位间距3050 m,站位之间的平均水深约6 m (图 2).
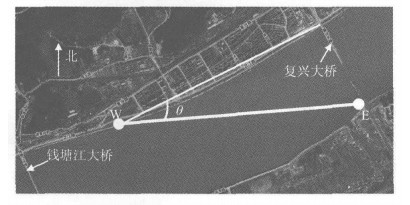
|
图 2 图 2实验站位示意图 W和E站表示双向声传播实验的两个站位,W和E连线表示声传播的路径,同时也是ADP走航的线路. Fig. 2 Location map of the experiment site W and E are two acoustic stations.The line between W and E represents the sound transmission path, and also the track of the ADP shipboard surveys. |
双方向声传播实验中声信号的发送与接收采用了两台沿海声层析仪(Coastal Acoustic Tomography System, 日本广岛大学生产,以下简称CATS, 详细参见参考文献[11]).两台CATS分别设置在W和E站(图 2).收发两用的换能器用绳索设置在水中,其深度约为3 m.双向声传播实验使用的声信号为5 kHz的10阶M序列信号,信号长614 ms, 每3 min同时向对方站位发送一次声信号,并接收对方发送的声信号,随后进行相关处理.数据存储于其内部的SD卡.
第一阶段实验从4月8日11:00到9日10:00, 历时23 h.在双向声传播实验观测的同时,进行了4次走航ADP (Acoustic Doppler Profiler,1.5 MHz,SonTek/YSllnc.)流速观测.第二次实验从5月8日12:00到10日7:00, 历时43 h.期间进行8次走航ADP流速观测.ADP观测的层厚为0.5 m,共22层,采样频率为5 s.
4 结果 4.1 ADP观测结果图 3是12次ADP走航观测得到的沿W-E方向的流速断面分布(VADP).第1〜2, 第8〜9和第12航次的流速都为正,即从W站流向E站1东向流).第3〜4, 第6和第10航次的流速都为负,即从E站流向W站(西向流).第5航次的走航观测是从W站驶向E站,由于钱塘江涌潮的到来导致VADP流向发生逆转,西面流速为正(东向流),东面为负(西向流).而第7和第11航次断面流速西面为负(西向流),东面为正(东向流),这是因为退潮使VADP流向发生逆转.其中第7航次处于涨潮转为退潮的阶段,平均流速约为0.第1〜2, 第9航次都是处于钱塘江平潮的阶段,平均流速比较大,都大于0.30 m/s.每个航次观测的断面平均流速(VADP)见表 1.
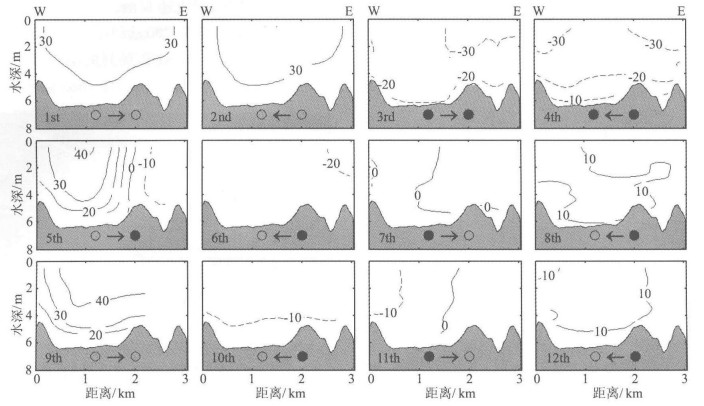
|
图 3 图 3断面流速分布 东方向(从W→E)流速为正(图中实线),西方向(从E→W)流速为负(图中虚线).流速等值线间隔为10 cm/s,航次在图的左下方表示.图中黑箭头表示船航行的方向.黑圈表示潮位最高,空圈表示潮位最低. Fig. 3 Vertical sections of the current velocity The positive (solid line) and negative (dotted line) value indicates the eastward (W→E) and westward (E→W) velocity, respectively.The contour interval is 10 cm/s.The cruise numbers are indicated in the bottom left corner of each panel.The black arrows show the directions of the shipboard survey.The black and white dots show the highest and lowest tide, respectively. |
|
|
表 1 ADP走航观测得到的断面平均流速(VADP)、流量(QADP)和声传播观测得到的平均流速(VCATS) Table 1 Average speed (VADP) and discharge (QADP) by ADP and the average speed (VCATS) by reciprocal sound transmission |
通过W-E断面的流量可由下式得到:
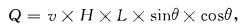
|
(7) |
其中v是沿声传播路径的平均流速,θ是W-E与钱塘江岸的夹角(25°,参见图 2), H=5.79 m (ADP底跟踪数据的平均值)和L=3050 m分别是钱塘江平均水深和两个站位之间的距离.12个航次ADP观测得到的流量QADP见表 1.
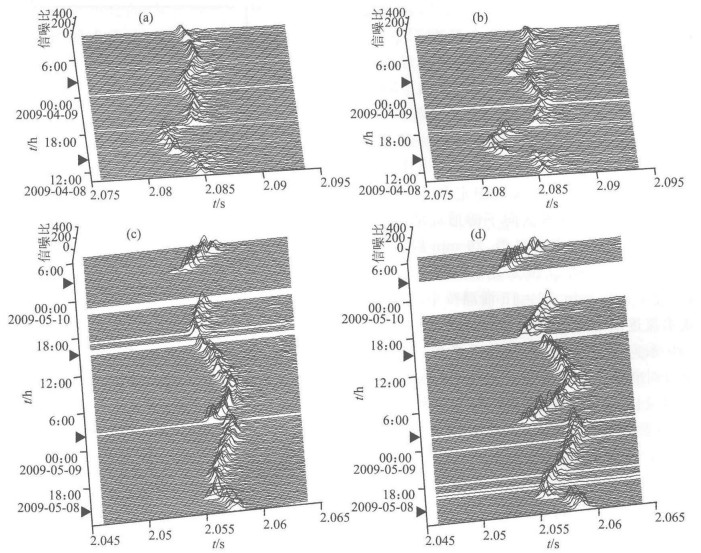
4.2 双向声传播观测结果图 4是W和E站接收到信号信噪比(Signal-to-Noise Ratio, 以下简称SNR)的时间序列.图 4(a,b)中,实验第一阶段的SNR在2.08〜2.09s之间有非常明显的峰值出现,这与预计声信号到达的时间基本一致(3050 m/1482 m/s=2.06 s在20℃的淡水中声速为1482 m/s).图 4(c,d)中的实验第二阶段SNR的峰值平均都超过130(21dB),最大为320(25 dB).由于2009年5月9日21:00到10日3:00W站的CATS出现停机,导致SNR序列图中的数据缺失.其他因GPS没有接收到信号等原因导致图 4中少部分数据的缺失.
|
图 4 SNR时间序列 图中的黑箭头表示涌潮到来的时刻(现场目测)(a) E站(实验第一阶段);(b) W站(实验第一阶段);(c) E站(实验第二阶段);(d) W站(实验第二阶段) Fig. 4 The time series of SNR The triangles indicate the arrive time of the tidal bore (visual observation). |
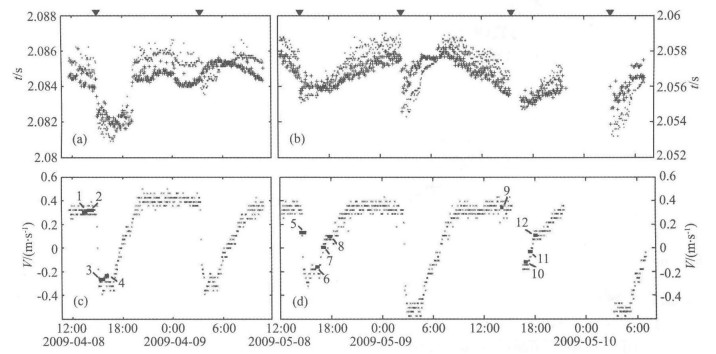
图 5是双向声传播时间以及根据式(3)得到的声传播路径上的平均流速.从图 5(a, b)中看出,在涌潮到来前后传播时间相应的发生了非常大的变化,涌潮的到来使双向声传播时间缩短.
|
图 5 CATS测得的双向传播时间和流速时间序列 (a,b):‘o’和‘ + ’表示双方向的声传播时间.图上方的黑箭头与图 4相同.(c,d):‘x’表示双向声传播实验测得的流速,实线表示ADP走航观测得到的平均流速.实线所对应的数字表示ADP的航次. Fig. 5 The reciprocal travel times measured by CATS and time series of water velocities in our observation (a, b):'o' and '+' indicate the travel lime of reciprocal sound transmission.The triangles at the top of panels are same as Fig.4.(c, d):'x' indicate the velocities measured by the reciprocal sound transmission experiment.Horizontal lines indicate the mean velocities measured by ADP.The cruise numbers (1 to 12) are indicated near the horizontal lines. |
在水中声速以及流速都会影响声传播时间,而流速远远小于声速,声传播时间主要受到声速的影响.声速受温度、盐度和压力的影响.在实验区域内进行CTD测量表明实验期间盐度为0,压力的变化小于1 m,盐度对声速无影响,压力对声速的影响很小(小于0.02 m/s).涌潮的到来使双向传播时间都变小,表明实验区域的水温升高,下游江水的温度高于上游江水的温度.
每次ADP走航期间声传播观测获得流速的平均值(VCATS)见表 1.在表 1中用ADP走航期间观测的断面平均流速(VADP)与该走航期间声传播观测获得流速的平均值(VCATS)进行比较.两者的时空尺度不完全一致.河道中的流速若变化均匀,两者基本吻合.第5航次ADP的走航正好处于涌潮到来的时段,流速变化急剧,导致两者之间差异增大.
从图 5(c,d)中可以看出VCATS与VADP基本一致,除了第5航次两者相差0.06 m/s以外,其他航次相差最大不超过0.05 m/s.12个航次VCATS与VADP的均方差为0.03 m/s.从图 5(c,d)中明显可看出在4月8日14: 10〜19: 30, 4月9日2: 30〜 9:15, 5月8日14:30〜19:40, 5月9日2:30〜 8:15和5月9日15:20〜21:30涌潮的到来引起了流速流向的明显变化.例如,图 5c中4月8日14:10(图 5c中的箭头)之前,流速稳定在0.32 m/s (东向流),这是上游的淡水流向下游形成的.涌潮(西向流)与淡水的流速逐步抵消,20 min以后,西向流达到最大,约为-0.27 m/s.之后西向流趋于平稳,大约持续1 h 45 min.16:15涌潮减小,上游往下游的淡水流逐渐起主导作用,西向流转变为东向流,19:30东向流达到最大,并趋于平稳,持续约7 h.涌潮的到来是个较为短暂的过程,但是涌潮影响持续时间较长.涌潮首先使稳定东向流转变为西向流,随后其影响慢慢消退,直至完全消失.整个过程持续了5 h 20 min.
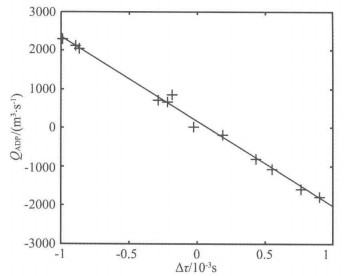
4 流量和声传播的关系图 6是12个航次的断面流量QADP与ADP走航期间双向声传播实验平均△τ的关系图.图中可以看出QADP与△τ有较好的线性关系,用最小二乘法得到△τ与QCATS的线性关系式:
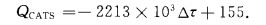
|
(8) |
|
图 6 双向传播时间差(△τ)与断面流量(QADP)的关系 ‘+’表示ADP观测得到的断面流量QADP,其横轴对应ADP各个走航期间的平均△τ.实线表示由最小二乘法得到的△τ和QCATS的关系. Fig. 6 Correlation between the travel time differences (△τ) and the river discharges (QADP) '+' indicate QADP, the horizontal axis indicate △τ corresponding to the ship-board ADP surveys.Solid line indicates the liner relationship derived from the least square method. |
12个航次的断面流量QADP与式(8)得到的同一时刻QCATS的均方差为108 m3/s.这与式(7)中代入VCATS与VADP之间的均方差0.03 m/s,得到的流量均方差203 m3/s不一致.203 m3/s与108 m3/s都是12次VADP计算得到的流量与12次VCATS计算得到的流量之间的均方差.其中所用的ADP流量没有经过线性回归.108 m3/s是用经过线性回归的CATS流量求得,203 m3/s是用没有经过线性回归的CATS流量求得.线性回归对变化较大的流量进行了平滑,使均方差变小.
图 7是由式(8)得到的断面流量时间序列.由于涌潮到来钱塘江水的倒灌,导致QCATS在4月8日14:30〜16:15, 4月9日3:00〜4:30, 5月8日15:00〜16:40, 5月9日3:00〜4:30和5月10日3:30〜5:00出现流量的极小值.最小出现在5月9日3:00〜4:30之间,为-3406 m3/s.而钱塘江上游往下游的淡水输送,导致QCATS在4月8日10:40〜14:10, 4月8日19:30至9日2:30, 5月8日12:00〜14:30, 5月8日19:40至9日2:30, 5月9日8:15〜15:20出现流量的极大值.淡水输送流量最大出现在4月8日19:30至9日2:30之间,为3509 m3/s.钱塘江的净流量用日分潮周期(24小时50分钟)内流量的平均值表示,第一阶段实验为1329 m3/s,第二阶段实验为979 m3/s.图中QADP (粗线表示)与QCATS (细线表示)基本吻合.
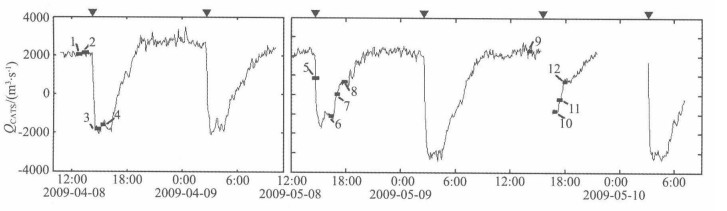
|
图 7 QCATS的时间序列(9 min平滑) 图中曲线表示CATS数据计算所得的流童,直线表示ADP观测得到的流量.图上方的三角与图 4相同. Fig. 7 Time series of QCATS (9 minutes smoothing) The curves indicate the river discharge calculated by CATS, the horizontal lines indicate the river discharge calculated by ADP.The triangles are same as Fig.4. |
关于QCATS的绝对误差来源于ADP的观测误差以及声传播的观测误差两个部分.若只考虑声传播的观测误差,QCATS的误差只是相对ADP观测的误差,没有实际意义.故必须把ADP精度包括进去.
QCATS的绝对误差(折算成流速误差)主要有以下几个方面:(1)公式(8)经验回归的误差为108 m3/s,折算成流速误差为vEr1=0.016 m/s; (2) ADP直接观测误差(用户手册中仪器观测精度)=0.005 m/s[12]; (3) ADP走航时,因指南针偏差(经DGPS矫正)而引起的流速误差为vEr3=0.O1l m/s; (4)双向声传播实验系统时钟误差为0.5μs[11],折算成流速误差vEr4=0.000 m/s; (5)双向声传播系统的米样精度为0.1 ms, 折算成流速误差vEr5=0.036 m/s.以上5个方面的误差合计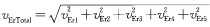
2009年4月8日至9日和2009年5月8日至10日,两台用于声信号发送和接收的双向声传播实验系统分别设置在钱塘江两岸的W和E站,进行了双方向声传播测流实验.与此同时,沿着W-E断面进行了12次走航ADP流速观测.本文的主要结论总结如下:
(1) VCATS与VADP基本一致,两者之差最小为0, 最大为0.06 m/s,均方差为0.03 m/s.其中第5航次观测期间,涌潮的到来使得流速的变化比较大,导致VCATS与VADP差达到了0.06 m/s.
(2) △τ与QADP有良好的线性关系,利用最小二乘法得到两者之间的经验公式,由此推算出在观测期间QCATS的时间序列.
(3)观测期间QCATS最小为-3406 m3/s,这是涌潮到来钱塘江水倒灌的流量.QCATS最大为3509 m3/s,这是钱塘江从上游往下游的淡水输送量.第一阶段实验期间钱塘江的净流量为1329 m3/s,第二阶段为979 m3/s.
(4)双向声传播方法的流量测量误差折算成流速误差为0.041 m/s,其中双向声传播系统引起的误差达到0.036 m/s,约占总误差的77%,为主要误差源,经验回归所引起的误差达到0.016 m/s,约占总误差的15%,为次要误差源.
在我国沿海海域和长江、钱塘江等大型河道,用常规的测流方法常常受繁忙的船舶航行等限制,很难实现对流速和流量长期、连续的实时监测.以上结论表明双向声传播测流法可以取代常规的测流方法应用于大型河道流速和流量监测,可在我国大型河道水资源的管理、环境监测和防灾减灾等方面发挥重要作用.
致谢感谢国家海洋局第二海洋研究所张涛、廖光洪参加了部分野外实验工作,感谢审稿人对本文提出的意见和建议.
| [1] | 林辉勇. 声学多普勒流速剖面仪在河流水文测验中的应用. 中国水利 , 2003, 9(B): 37–39. Lin H Y. Application of ADCP for river hydrometry. China Water Resources (in Chinese) , 2003, 9(B): 37-39. |
| [2] | 陆宝宏, 祁昌军, 胡震云, 等. 大型深水库流速比测方法研究及比测结果相关性分析. 水利学报 , 2007, 10(Suppl.): 360–364. Lu B H, Qi C J, Hu Z Y, et al. Research on the methods of velocity comparative measurement and correlation analysis of the comparative observed results in large scale deep-water reservoirs. Journal of Hydraulic Engineering (in Chinese) , 2007, 10(Suppl.): 360-364. |
| [3] | Kaneko A, Yamaguchi K, Yamamoto T, et al. A coastal acoustic tomography experiment in the Tokyo Bay. Acta Oceanologica Sinica , 2005, 24(1): 86-94. |
| [4] | 何菊梅. 水位流量关系的确定方法及误差检验. 水利科技与经济 , 2008, 14(9): 700–701. He J M. The methods of determine stage-discharge relation and examine error. Water Conservancy Science and Technology and Economy (in Chinese) , 2008, 14(9): 700-701. |
| [5] | 李效贤. 大型渠道超声波法与流速仪法测流比对试验. 中国农村水利水电 , 2006, 8: 107–112. Li X X. The flow measurement comparison test of ultrasonic method and the flow meter in Large channel. China Rural Water and Hydropower (in Chinese) , 2006, 8: 107-112. |
| [6] | 孙国志, 赵文通, 刘俊龙. 超声波流量计的工程设计及应用. 齐齐哈尔大学学报 , 2002, 18(2): 72–74. Sun G Z, Zhao W T, Liu J L. Application engineering of ultrasonic wave. Journal of Qiqihar University (in Chinese) , 2002, 18(2): 72-74. |
| [7] | Zheng H, Gohda N, Noguchi H, et al. Reciprocal sound transmission experiment for current measurement in the Seto Inland Sea, Japan. Journal of Oceanography , 1997, 53: 117-127. |
| [8] | Kawanisi K, Watanabe S, Kaneko A, et al.River acoustic tomography for continuous measurement of water discharge.Proc.3rd International Conference & Exhibition on "Underwater Acoustic Measurements:Technologies & Results, 2:613~620 |
| [9] | 朱小华, 郑红, 廖光洪, 等. 沿海声层析仪的设计与实现. 哈尔滨工程大学学报 , 2010, 31(1): 64–68. Zhu X H, Zheng H, Liao G H, et al. Design and implementation of coastal acoustic tomography. Journal of Harbin Engineering University (in Chinese) , 2010, 31(1): 64-68. |
| [10] | Munk W, Worceser P F, Wunsch C. Ocean Acoustic Tomography. Cambridge: Cambridge University Press, 1995 : 1 -433. |
| [11] | 朱小华, 江田憲彰, 吴清松, 等. 一种浅水河道声学测流仪. 电子测量技术 , 2009, 32(2): 166–169. Zhu X H, Gohda N, Wu Q S, et al. Acoustic current meter for measurement of velocity in a shallow channel. Electronic Measurement Technology (in Chinese) , 2009, 32(2): 166-169. |
| [12] | Sontek.Current Surveyor System Manual:Software Version 4.30.San Diego, California.2005.160 |
 2010, Vol. 53
2010, Vol. 53



