2. 中国科学院研究生院, 北京 100049;
3. 东北石油大学地球科学学院, 大庆 163318
2. Graduate University of Chinese Academy of Sciences, Beijing 100049, China;
3. College of Earth Sciences, Northeast Petroleum University, Daqing 163318, China
目前,关于地震资料中多次波问题的处理有两种思路,即多次波成像和多次波压制.但由于多次波成像的方法尚未成熟,所以在绝大多数情况下,仍将多次波作为噪声予以压制.基于波动方程的表面多次波压制方法通常要由多次波预测和自适应相减两步实现.由已知的总波场通过褶积法可预测地震数据中的多次波,而分离多次波和其他的地震反射同相轴要借助于自适应相减方法,即从原始数据中自适应减去预测的波场,完成多次波的压制[1],相减过程用于补偿预测误差[2],即补偿预测过程中出现的频率、振幅、相位上的误差.基于波动方程压制表面多次波的预测减去法[3]可由级数法或迭代法实现,因为级数展开法的计算量很大,且可预测的项数有限,故本文应用迭代法进行多次波压制,此外,迭代法还可以和其他多次波压制方法结合使用,进一步提高多次波压制效果.
多次波预测与相减的任何一个环节,都对多次波压制效果起着至关重要的作用,预测过程获得了多次波的运动学特性(走时),自适应相减过程获得了多次波的动力学特性(振幅和波形)[4].为了更好地进行表面多次波压制,文中在多次波预测和相减过程中均采用迭代算法,综合了以往只进行迭代预测[5, 6]或只进行迭代相减[7]的优势,在迭代过程中,描述多次波运动学和动力学特性的参数能更好地与实际的多次波相匹配.迭代预测,较好地校正了多次波走时误差,迭代相减,增加了滤波器长度,可在保持有效波振幅条件下更好地压制多次波.
很显然,迭代方法的应用将使多次波压制的计算量大为增加,为提高计算效率,文中借助于GPU(Graphic Processing Unit)在高度密集型科学计算方面具备的高速度和高性能的优势[8~10],采用GPU/CPU协同并行计算压制表面多次波,即在GPU上应用CUDA(计算机统一设备架构)编程语言实现表面多次波预测的并行计算,在CPU上完成多次波自适应匹配相减,GPU/CPU协同并行计算可使多次波预测获得优异的加速比,为实现迭代预测和迭代相减提供了计算速度的保障.
已有学者开展了表面多次波自适应相减方面的工作[11~18],在不同的假设条件下有着不同的处理优势.文中将高频重建的思想引入到表面多次波自适应相减中,利用高频重建的多次波模型以改善预测多次波的频率特性,也利用了Hilbert变换的多次波模型以校正预测多次波的相位误差,利用平移的多次波模型以补偿预测多次波的振幅特性.高频重建思想的引入以及上述三种方法的有效结合应用,改善了预测表面多次波过程中产生的多余的子波效应,使得表面多次波的动力学特性得到很好的拟合,从而获得较好的多次波压制效果.
2 基本理论 2.1 GPU加速迭代法表面多次波预测对于表面多次波预测,级数法与迭代法都属于基于波动方程的反馈迭代方法,由产生表面多次波的反馈模型导出.应用级数法预测高阶的多次波,需要较大的计算量,多次波预测的迭代形式表述简洁,且能预测所有阶多次波.本文采用迭代法预测表面多次波,一般来说迭代2~3次便可获得较好的压制效果.
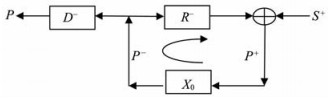
基于Berkhout的WRW物理模型[19],多次波的产生过程利用反馈模型可表示为图 1,含多次波的波场可表述为

|
(1) |
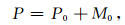
|
(2) |
|
图 1 表面多次波的正演模拟 Fig. 1 The modeling of surface-related multiple |
式中:P0和M0分别表示一次波和多次波;P-为上行波场;S+为下行的震源波场;X0为自由界面不发生反射时的地下介质的脉冲响应;R-为上行波场在自由界面处的反射算子;D-为描述检波器特性的算子.一次波由震源波场经一次反射产生,即
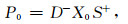
|
(3) |
若将一次波场作为震源再次反射后,生成多次波场,即
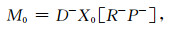
|
(4) |
易知,下行波场P+为

|
(5) |
由
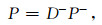
|
(6) |
综合以上表述,易知
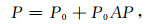
|
(7) |

|
(8) |
式中,A为自由界面算子.
由上可知,依据当前一次波的估计值和含表面多次波原始数据的褶积可预测表面多次波,其表述为
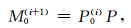
|
(9) |
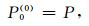
|
(10) |
式中,P0(i)为一次波的估计值.一次波的初始迭代值可以是包含多次波的原始地震波场,也可以是其他方法(如Radon变换法、速度滤波法等)的多次波衰减结果,本文采用前者.与波场中实际的多次波相比,预测的多次波M0(i+1)在振幅、相位和频率上均存在误差,需要在多次波相减过程中加以校正,自适应匹配相减是补偿上述误差的较好方法,GPU预测的多次波场将作为自适应相减算法的输入.
为更好地改善多次波的运动学特性,可迭代进行多次波预测,然而,迭代的应用使得多次波压制的整个计算过程效率较低,而且,每次迭代都要在频域的每个频率分量上做大规模的矩阵乘法运算,也需要较高的计算成本.基于波动方程表面多次波预测涉及的矩阵乘法运算非常适合应用CUDA语言在GPU上并行计算实现,本文利用GPU/CPU协同并行计算预测多次波,节省了多次波压制的计算成本,从而提高了多次波预测的计算效率,在算法实现过程中,共享存储器的有效应用,也对GPU的计算能力进行了充分挖潜.利用同样的算法计算含多次波的SMAART模型,与CPU相比,利用GPU可获得约70倍的加速比.
2.2 自适应匹配滤波法表面多次波衰减对基于波动方程的预测相减多次波压制方法,多次波减法是决定多次波压制效果的重要环节之一.在匹配相减方法的发展中,先后出现了单道匹配相减法、常规多道匹配相减法、伪多道匹配相减法和扩展多道匹配相减法等四类方法.多次波相减方法的重点之一是改变多次波模型道的属性,使其与真正的多次波相匹配.本文由原始的多次波模型道导出用于匹配滤波的多次波模型道,所以该方法属于伪多道匹配滤波范畴.该方法的主要思想是由原始数据通过GPU预测表面多次波,依据每一道多次波模型,导出其他衍生的多次波模型道,由多道匹配滤波方法计算出多道匹配滤波器,并将其应用到多次波模型道上,计算出线性组合的多次波模型,再将其从原始数据中减去,得到压制后的多次波.
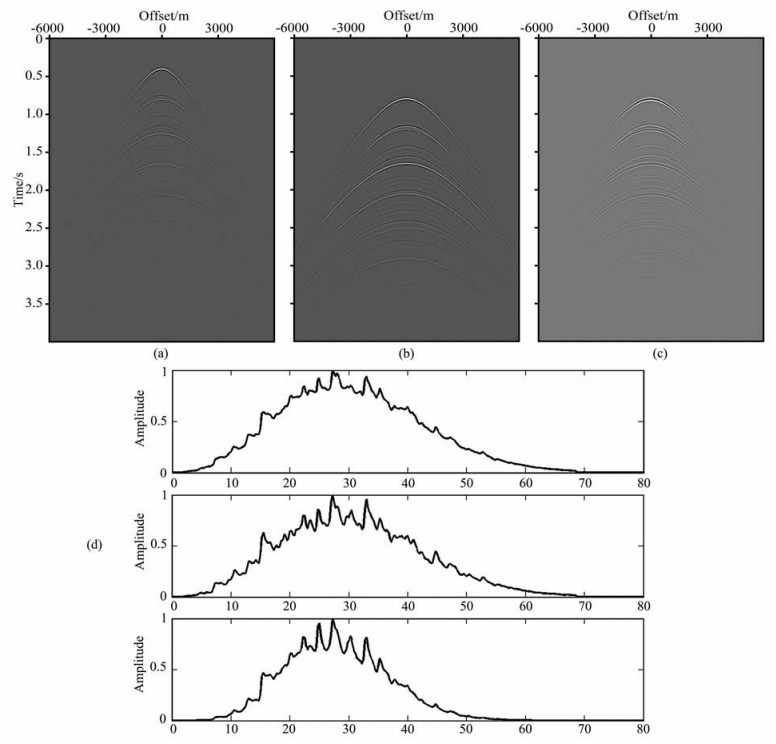
由于预测过程中多余的子波效应,使得预测的多次波高频成分能量微弱,直观上来说,预测的多次波频带比波场中实际的多次波频带窄,图 2给出了单炮记录的频谱分析,其中图 2a为一维介质模拟的含有二阶表面多次波的单炮记录,图 2b为炮记录中实际的多次波,图 2c为预测的多次波,对比图 2b与图 2c的多次波炮记录剖面,分析可知预测的多次波具有主频低、频带窄的特点,从图 2d的频谱分析中,可明显看出预测的多次波与实际多次波的频率特性的差异.
|
图 2 单炮地震记录频谱分析 (a)总波场;(b)实际的多次波;(c)预测的多次波;(d)依次对应(a)、(b)、(c)频谱对比分析图. Fig. 2 Spectrum analysis for one shot seismic record (a) Total wavefield; (b) Actual multiple; (c) Predicted multiple; (d) Spectrum analysis comparison for (a), (b), (c) in sequence. |
对图 2分析认为,预测多次波与实际总波场频宽上的能量不匹配,所以去子波效应是多次波自适应相减过程的一个关键环节.本文采用高频重建[20, 22]的方法补偿预测多次波的高频信息,使得匹配后多次波频带上的能量更接近于实际多次波的频带能量,从而消除了预测过程中多余的子波效应.
自适应匹配滤波方程可表示为
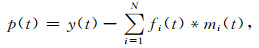
|
(11) |
式中:p(t)为衰减多次波后的地震数据道;y(t)为原始数据道;N为多次波模型道的道数;mi(t)(i=1,…,N)分别表示预测的多次波模型道、多次波模型道的高频重建道、多次波模型道的Hilbert变换道,以及它们的上平移和下平移道,其他各道均由多次波模型道导出;fi(t)为维纳整形滤波器,*表示褶积;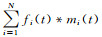
假定压制多次波后地震记录的能量最小,则自适应滤波器的求取可通过求式(11)的最小二乘解来获得,即
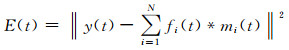
|
(12) |
最小,将褶积形式表示成矩阵与向量相乘,最后求解线性方程组可获得自适应滤波器fi(t).
在自适应相减过程中进行迭代,可增加滤波器的长度,提高自适应匹配相减的精度,进而改善多次波压制效果.
以单道匹配为例,原始自适应匹配方程为

|
(13) |
则我们可以构造迭代相减方法为
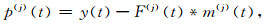
|
(14) |
首次多次波模型m(t)在预测阶段生成.其中,j为减法迭代次数,F(j)(t)表示与f(j)(t)相关的匹配滤波器.
同时,我们可以构造多次波迭代模型
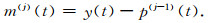
|
(15) |
值得指出的是,在迭代过程中,维纳滤波器是最优可取的,从而保证了迭代算法的收敛性[23].
以两次迭代为例,有效波迭代格式为

|
(16) |
其中F(2)(t)=f(2)(t)*f(1)(t)为实际的匹配滤波器,从而迭代增加了滤波器的长度,如果令每次迭代中滤波器的长度为l,则最终的滤波器长度将为2l-1,远远大于单个滤波器长度,由于长滤波器能消除更多的多次波能量,但无法保护一次波,所以如果直接应用长滤波器,虽然可以压制更多的多次波,但一次波将受到损害.若直接应用短滤波器,则多次波能量会出现较大残余,所以往往在压制多次波和保护一次波之间需要一个折中.通过迭代方法实现多次波减法,应用稍短的滤波器,在保护有效波的同时,却可以获得长滤波器的优点,使多次波得到有效的压制.在自适应相减的过程中,滤波器长度可根据地震资料情况进行调节,合适的参数将会得到更好的压制结果,通常迭代2~3次即可取得满意的多次波压制效果.
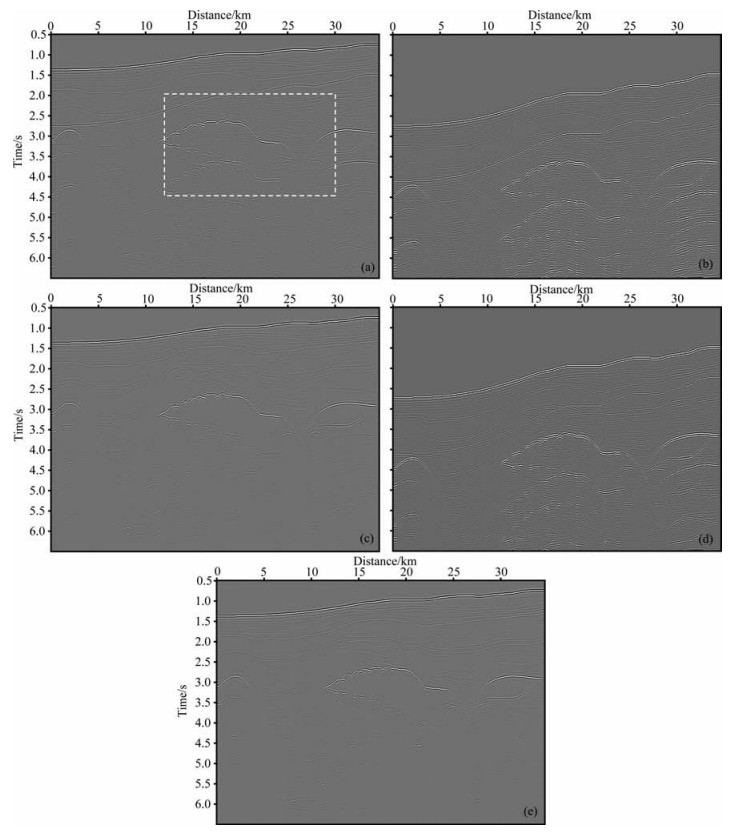
3 SMAART模型表面多次波压制为了验证本文方法压制表面多次波的有效性,对含强表面多次波的SMAART合成数据体进行了试算,该模型含能量很强的高阶水底表面多次波和3个盐丘顶底界面的表面多次波,如图 3a所示.采用文中方法,利用GPU预测每个频率切片上的多次波,迭代一次预测的多次波共零偏移距剖面如图 3b所示,水底表面多次波和盐丘顶底界面的表面多次波被很好地预测出来,利用此预测的多次波模型,迭代一次相减的表面多次波压制结果如图 3c所示,多次波能量在一定程度上得到压制,但仍可见部分残余能量.
|
图 3 SMAART模型表面多次波压制 (a)原始数据共零偏移距剖面;(b)迭代一次的多次波预测结果;(c)迭代一次的多次波压制结果;(d)迭代两次的多次波预测结果;(e)预测迭代两次,每次预测后相减迭代两次的多次波压制结果. Fig. 3 Surface-related multiple suppression on synthetic SMAART model (a) Common zero-offset profile for raw data; (b) Multiple prediction result after one iteration; (c) Multiple suppression result after one iteration; (d) Multiple prediction result after two iteration; (e) Multiple suppression result after two iteration subtraction after two iteration prediction. |
将图 3b所示首次估计的多次波模型,用于自适应相减中,迭代相减两次得到衰减多次波的数据,再将此有效波估计和原始含多次波数据预测表面多次波,图 3d为第二次迭代预测的共零偏移距剖面,若再将此结果作为自适应相减的输入,得到预测两次且每次预测相减迭代两次的多次波衰减结果,对比可知,迭代两次的多次波压制效果较迭代一次的有明显改善,强能量的水底表面多次波和盐丘表面多次波均得到了有效的压制,同时有效波的振幅得到很好的保持.
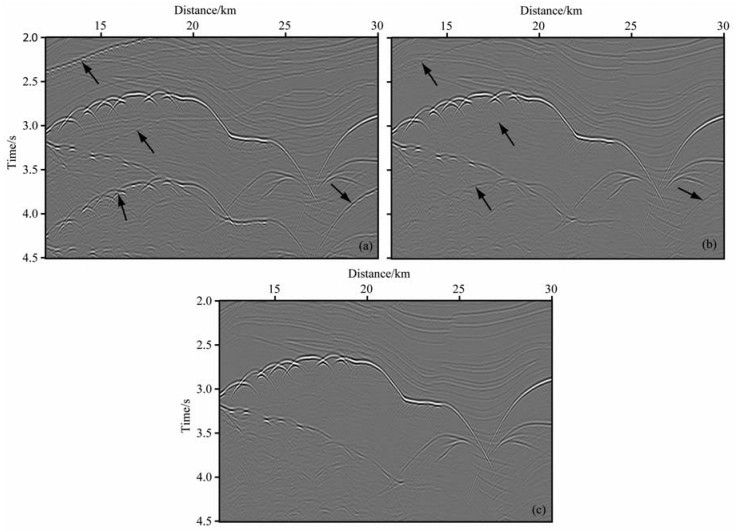
将图 3a所示的框内区域以及图 3b和3c的相应区域进行局部放大显示,如图 4a,4b和4c所示.观察图 4a箭头所指的海底多次波能量和盐丘多次波能量,经过一次迭代后,得到了一定程度的衰减,如图 4b所示,经过预测和相减的两次迭代后,多次波能量基本上得到了有效的压制,如图 4c所示.
|
图 4 图 3的局部放大 (a)图 3a的局部放大显示;(b)图 3c的局部放大显示;(c)图 3e的局部放大显示. Fig. 4 Partial zoom-in of Fig.3 (a) Partial zoom-in of Fig.3a; (b) Partial zoom-in of Fig.3c; (c) Partial zoom-in of Fig.3e. |
应用本文多次波压制计算方法,对中国某深水海域的二维地震资料进行了表面多次波压制试算.该资料的采样间隔为4 ms,采样点为1150,也就是说记录长度为4.6s,炮间距为26m,每炮180道接收,道间距26m,最小偏移距为208m.该资料采集的地震地质条件较好,海底相对较为平坦.从图 5a所示共近偏移距剖面上可看出,双程走时大于3.5s的剖面上存在着能量较强的表面多次波(如图中箭头所示),本文对深海采集的部分炮记录(300炮)的地震资料进行了表面多次波压制的预处理,图 5b~5d分别为迭代一次、两次和三次的表面多次波压制结果,分析可知,一次迭代便可见到较为明显的多次波压制效果,也就是说多次波的能量大为减弱.两次迭代后表面多次波能量得到有效压制,同时海洋地震资料多次波压制试算表明,在压制表面多次波的同时,深层地震有效波的振幅基本未受到任何影响.

|
图 5 实际海洋地震数据多次波压制 (a)含表面多次波的共偏移距剖面; (b)迭代一次多次波压制结果; (c)迭代两次多次波压制结果, 每次预测后相减迭代两次的多次波压制结果; (d)迭代三次多次波压制结果, 每次预测后相减迭代三次的多次波压制结果. Fig. 5 Multiple suppression of real marine seismic data (a) Common offset profile with multiples; (b) Multiple attenuation result after one iteration; (c) Multiple suppression result after two iteration subtraction after two iteration prediction; (d) Multiple suppression result after three iteration subtraction after three iteration prediction. |
本文充分利用GPU在高性能科学计算方面的优势,由GPU/CPU协同并行计算完成表面多次波的压制,具体由GPU完成每个频率分量上大尺寸的矩阵乘法运算,预测地震资料中的表面多次波,对于同样的算法,相比于CPU,利用GPU计算可获得较高的加速比,使得迭代算法计算效率大为提高,对于复杂的SMAART模型,基于GPU并行预测的计算效率是传统基于CPU串行计算的70倍左右.文中运用迭代完成多次波的预测和相减,即多次波压制由迭代预测和迭代相减实现,通常2~3次迭代即可得到较好的表面多次波压制效果,预测步骤的迭代,改善了多次波正演过程中的运动学特性,自适应匹配相减过程迭代,改善了多次波的动力学特性,而且匹配相减中的迭代算法增加了匹配滤波器的长度,在保持有效波振幅的条件下可更好地压制多次波残余能量.本文利用高频重建补偿频带能量差异,使预测多次波高频带的能量更接近于实际波场中的多次波高频带的能量.平移信号的应用也更好地改善了多次波的振幅特性,从而获得较好的自适应匹配相减效果.
致谢本文部分研究内容受到地下信息探测技术与仪器教育部重点实验室(中国地质大学,北京)开放课题项目(GDL0903)资助,在此表示感谢.
| [1] | Wiggins J W. Attenuation of complex water-bottom multiples by wave-equation-based prediction and subtraction. Geophysics , 1988, 53(3): 1527-1539. |
| [2] | Van Groenestijn G J A, Verschuur D J. Estimation primaries by sparse inversion and application to near-offset data reconstruction. Geophysics , 2009, 74(3): 23-28. |
| [3] | Verschuur D J, Berkhout A J. Adaptive surface-related multiple elimination. Geophysics , 1992, 57(9): 1166-1177. DOI:10.1190/1.1443330 |
| [4] | Luo Y, Kelamis P G, Aramco S, et al. Simultaneous inversion of multiples and primaries:inversion versus subtraction. The Leading Edge , 2003, 20: 814-819. |
| [5] | Verschuur D J, Berkhout A J. Estimation of multiple scattering by iterative inversion, partⅡ:Practical aspects and examples. Geophysics , 1997, 62(5): 1596-1611. DOI:10.1190/1.1444262 |
| [6] | Berkhout A J, Verschuur D J. Estimation of multiple scattering by iterative inversion, partⅠ:Theoretical considerations. Geophysics , 1997, 62(5): 1586-1595. DOI:10.1190/1.1444261 |
| [7] | Huo S D, Wang Y H. Improving adaptive subtraction in seismic multiple attenuation. Geophysics , 2009, 74(4): v59-v67. DOI:10.1190/1.3122408 |
| [8] | 李博, 刘国峰, 刘洪. 地震叠前时间偏移的一种图形处理器提速实现方法. 地球物理学报 , 2009, 52(1): 245–252. Li B, Liu G F, Liu H. A method of using GPU to accelerate seismic pre-stack time migration. Chinese J. Geophys. (in Chinese) , 2009, 52(1): 245-252. |
| [9] | 刘国峰, 刘洪, 李博, 等. 山地地震资料叠前时间偏移方法及其GPU实现. 地球物理学报 , 2009, 52(12): 3101–3108. Liu G F, Liu H, Li B, et al. Method of prestack time migration of seismic data of mountainous regions and its GPU implementation. Chinese J. Geophys. (in Chinese) , 2009, 52(12): 3101-3108. |
| [10] | Zhang J H, Wang S Q, Yao Z X. Accelerating 3D Fourier migration with graphics processing units. Geophysics , 2009, 74(6): WCA129-WCA139. DOI:10.1190/1.3223186 |
| [11] | Lu Wen-Kai, Berkhout A J. Adaptive subtraction using independent component analysis. Geophysics , 2006, 71(5): 179-184. DOI:10.1190/1.2243682 |
| [12] | Lu Wen-Kai, Liu Lei. Adaptive multiple subtraction based on constrained independent component analysis. Geophysics , 2009, 74(1): 1-7. |
| [13] | 陆文凯, 骆毅, 赵波, 等. 基于独立变量分析的多次波自适应相减技术. 地球物理学报 , 2004, 47(5): 886–891. Lu W K, Luo Y, Zhao B, et al. Adaptive multiple wave subtraction using independent component analysis. Chinese J. Geophys. (in Chinese) , 2004, 47(5): 886-891. |
| [14] | 李鹏, 刘伊克, 常旭, 等. 均衡拟多道匹配滤波法在波动方程压制多次波中的应用. 地球物理学报 , 2007, 50(6): 1844–1853. Li P, Liu Y K, Chang X, et al. Application of the equipoise pseudomultichannel matching filter in multiple elimination using wave-equation method. Chinese J. Geophys. (in Chinese) , 2007, 50(6): 1844-1853. |
| [15] | Wang Y. Multiple subtraction using an expanded multichannel matching filter. Geophysics , 2003, 68(1): 346-354. DOI:10.1190/1.1543220 |
| [16] | Kaplan S T, Innanen K A. Adaptive separation of free-surface multiples through independent component analysis. Geophysics , 2008, 73(3): 29-36. DOI:10.1190/1.2890407 |
| [17] | Guitton A, Verschuur D J. Adaptive subtraction of multiples using L1-norm. Geophysical Prospecting , 2004, 52(1): 27-38. DOI:10.1046/j.1365-2478.2004.00401.x |
| [18] | Spitz S. Pattern recognition, spatial predictability, and subtraction of multiple events. The Leading Edge , 1999, 18(1): 55-58. DOI:10.1190/1.1438154 |
| [19] | Berkhout A J. Seismic Migration, Imaging of Acoustic Energy by Wave Field Extrapolation, PART B:Practical Aspects. Amsterdam:Elsevier Science Publishers, 1984 |
| [20] | 曾锐, 刘洪, 秦月霜, 等. 基于自动增益控制调制法的高频重建技术. 地球物理学进展 , 2007, 22(3): 850–859. Zeng R, Liu H, Qin Y S, et al. High frequency reconstruction technique based on auto gain control modulation. Progress in Geophysics (in Chinese) , 2007, 22(3): 850-859. |
| [21] | 刘贺, 刘洪, 刘红伟, 等. 基于反假频基函数的井震匹配快速算法. 地球物理学进展 , 2009, 24(4): 1431–1436. Liu H, Liu H, Liu H W, et al. Fast algorithm of well-seismic matching based on anti-alias base functions. Progress in Geophysics (in Chinese) , 2009, 24(4): 1431-1436. |
| [22] | 石颖, 刘洪. 最小加权范数插值与调制升频结合的地震数据重建研究. 地震学报 , 2010, 32(3): 340–350. Shi Y, Liu H. Seismic data reconstruction by combining minimum weighted norm interpolation and band extension via modulation. Acta Seismologica Sinica (in Chinese) , 2010, 32(3): 340-350. |
| [23] | 王彦飞. 反演问题的计算方法及其应用. 北京: 高等教育出版社, 2007 . Wang Y F. Computational Method for Inverse Problems and Their Applications (in Chinese). Beijing: Higher Education Press, 2007 . |
 2010, Vol. 53
2010, Vol. 53


