2. 中国科学院研究生院, 北京 100049
2. Graduate University of Chinese Academy of Sciences, Beijing 100049, China
海水热含量作为影响全球气候变化的重要因素,是表征海洋热状态以及海气相互作用的重要指标之一.海水热含量变化具有强烈的周年变化特征,与其相关的海水热膨胀是海平面变化的重要因素[1~3].此外,海水热含量变化与ENSO现象[4]、季风爆发[5]和台风活动[6]等密切相关,是影响长期气候预报的重要因素.因此,对海水热含量开展深入的研究是十分必要的.
热含量及其变化的传统计算方法,是利用实测的或海洋模式输出的温度数据通过积分计算得到[7],但该方法受积分深度的选择和温度数据的精度影响较大[8].此外,受海洋上观测条件的限制,实测温度数据的时空分辨率较低,这也制约了对全球范围海水热含量变化的研究.
随着卫星测高技术的发展,利用高时空分辨率的海平面变化信息获取海水热含量变化,成为一种新的方法.White和Tai[9]对测高得到的海平面变化和丢弃式深度温度计(XBT)观测得到的热含量变化进行回归分析后发现,在北半球大部分地区,两者的相关性大于0.6.Chambers等[8]利用海水密度、热膨胀系数和定压比热,建立起了海面高度变化与海水热含量变化之间近似线性的物理关系,并利用测高数据对北太平洋和北大西洋的热含量变化进行了计算,与气候态温盐模型计算的结果进行了比较. Wang和Koblinsky [10]研究发现,利用TOPEX/ Poseidon卫星的测高资料计算的热含量变化与XBT观测得到的结果在北大西洋符合较好.在赤道太平洋地区,Chambers等[4]对卫星测高确定的海水热含量变化与热带海洋大气阵列(Tropical Ocean Atmosphere Array,TAO)量测的热含量变化进行了比较,并认为在全球大部分海洋地区利用测高资料计算得到的热含量是可靠的.佟景全等[5]基于卫星测高资料计算了我国南海地区的热含量变化,并与传统的计算方法进行了比较,同时分析了南海上层热含量异常的变化特征.Jayne等[11]模拟了GRACE(Gravity Recovery and Climate Experiment)重力卫星观测到的洋底压力(Ocean Bottom Pressure,OBP)变化,并结合海洋模式输出的海面高度数据,估算了海水热含量的变化.其模拟结果表明,考虑洋底压力变化的影响之后,热含量的估计精度有所提高.但Jayne等的工作局限在模拟阶段,利用实测数据进行验证的工作仍未见报道.另外,利用卫星测高技术分析海水热含量的工作主要集中在低纬度的开放海域地区,在高纬度地区及边缘海区域的研究仍不够充分.本文利用卫星测高数据、实测的气候态温盐场数据和模式的洋底压力数据,分析了全球和中国近海地区的热含量变化特征,与利用模式的时变温盐场数据计算的结果进行了比较分析,并对影响估计精度的各种误差源进行了详细的定量分析.研究结果表明,改进方法考虑了洋底压力变化以及热膨胀系数随海水深度变化的影响,提高了中高纬度地区的热含量估计精度.
2 基本原理与方法 2.1 比容海平面变化海水温度和盐度变化导致海水密度变化,进而引起的海平面变化称为比容海平面变化.其中由于温度变化引起的部分称为热比容海平面变化;由于盐度变化引起的部分称为盐比容海平面变化.根据Gill和Niiler[1]、Jayne等[11]的研究结果,比容海平面变化可以用以下公式表示
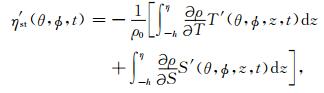
|
(1) |
其中,ρ0为海水平均密度,θ、ϕ和z分别为该点的经度、纬度和深度,t为时间,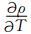
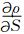
在忽略盐度变化影响的情况下,(1)式简化为
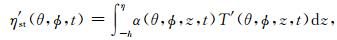
|
(2) |
其中,α=-∂ρ/(ρ0∂T)为海水热膨胀系数.假设其为与深度无关的常数α0,可以得到热比容海平面变化与海水温度变化之间的关系式为
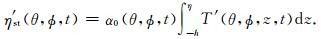
|
(3) |
海水热含量变化可以由(4)式表示[11]:
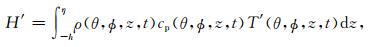
|
(4) |
其中ρ为海水密度,cp为海水定压比热,T′为海水温度的变化量.根据Wyrtki和Uhrich[12]、Chambers等[8]的研究结果,海水的密度和定压比热的乘积在不同温盐条件下的变化一般小于1%,可以作为常数处理.本文取ρ=1027 kg·m-3,cp=4000 J·kg-1·K-1.(4)式简化为

|
(5) |
结合(3)式和(5)式,得到海水热含量变化与热比容海平面变化之间的近似关系为
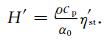
|
(6) |
(6)式中热膨胀系数α0的计算,利用了UNESCO(1981)推荐的海水状态方程[13]以及吉尔[14]附录3中的公式.采用不同方法计算的热膨胀系数有明显差异,是影响热含量估计的重要因素.不同计算结果的比较分析在3.3节给予讨论.
2.3 洋底压力(OBP)变化根据流体静力学原理,洋底某点的压力Pb可以表示为
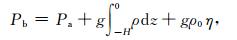
|
(7) |
其中,Pa为海表单位面积的大气压力,H为参考海平面到洋底的深度,g为万有引力常数,ρ为某一深度的海水密度,ρ0为海水平均密度,η为海平面高.
(7)式取微分,得到洋底压力变化Pb′为
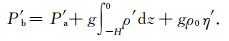
|
(8) |
海平面对大气压的响应可近似为反变气压计(inverted barometer)响应,具体公式为[15]
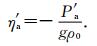
|
(9) |
公式(1)中的热比容海平面变化也可用(10)式表示为[16]
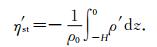
|
(10) |
将(8)式和(9)式代入(10)式,得
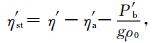
|
(11) |
其中,ηst′为热比容海平面变化,η′为测高卫星观测得到的海平面变化,ηa′为海表大气压变化引起的海平面变化(即反变气压计响应).利用(11)式即可以联合卫星测高数据和洋底压力数据得到热比容海平面变化,进而得到海水热含量变化.
3 数据处理分析 3.1 数据本文采用的卫星测高数据来自法国AVISO(the Archiving,Validation and Interpretation of Satellite Oceanographic data)数据中心发布的融合TOPEX/Poseidon(T/P)、Jason-1/2和ERS-1/2等多颗测高卫星得到的网格化数据[17].数据的时间间隔为7天,空间分辨率为(1/3)°×(1/3)°.该格网数据已经过必要的改正,包括潮汐改正、反变气压计改正等.本文采用的海洋模式数据为ECCO(Estimation of the Circulation and Climate of the Ocean)海洋模式提供的全球时变三维温盐场数据和洋底压力数据.热膨胀系数(Coefficient of Thermal Expansion,CTE)的计算主要采用了WOA05(World Ocean Atlas 2005)提供的气候态温盐场实测数据[18, 19].为了统一时空分辨率,方便计算结果的比较,本文对卫星测高数据和海洋数据进行了必要的月平均,空间分辨率均插值为1°×1°.ECCO海洋模式数据选取的时间跨度与测高数据相同,均为从2003年1月到2008年12月.
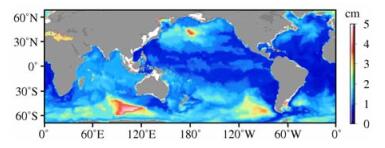
3.2 洋底压力(OBP)变化的全球分布选取了2003~2008年ECCO海洋模式提供的OBP数据,计算了OBP月变化量的均方差.图 1中的结果已转化为等效水柱高.由图 1可以发现,在北太平洋中部、印度洋东南部和太平洋东南部,OBP的月变化较为明显.
|
图 1 ECCO模式的洋底压力月变化量的均方差 Fig. 1 Root mean square of monthly OBP change from the ECCO model |
利用2003~2008年的ECCO海洋模式数据,采用公式(5)计算得到全球海水热含量月变化量的均方差,如图 2a所示.图中可以看到热含量变化明显的地区包括北大西洋的墨西哥湾流、北太平洋西部的黑潮和赤道西太平洋的暖池等.这些热含量变化较大地区的地理分布与Jayne等[11]的结果是一致的.

|
图 2 (a) ECCO模式得到的全球海水热含量月变化量的均方差; (b)利用测高数据和表面热膨胀系数计算得到的海水热含量月变化量的均方差; (c)利用测高数据和平均热膨胀系数计算得到的海水热含量月变化量的均方差; (d)利用测高数据、洋底压力数据和平均热膨胀系数计算得到的海水热含量月变化量的均方差 Fig. 2 (a) RMS of monthly heat content change from the ECCO model; (b) RMS of monthly heat content change from altimetry data and surface CTE; (c) RMS of monthly heat content change rrom altimetry data and averaged CTE; (d) RMS o f monthly heat content change from altimetry data, OBP data and averaged CTE |
利用2003~2008年的卫星测高资料,采用公式(6)计算得到海水热含量月变化量的均方差,结果如图 2b所示.其中热膨胀系数的计算,假定其为与海水深度无关的常数,并用海表的温盐数据来计算得到表面CTE[8].我们采用ECCO模式提供的表层温盐数据计算得到了表面CTE.比较图 2a和图 2b可以发现:在低纬度地区,该方法的估计精度相对较高;在中高纬度地区采用表面CTE引起的估计误差十分明显.
3.3.3 利用卫星测高数据和平均CTE估计热含量变化(方法二)在方法一的基础上,用平均CTE取代表面CTE,计算得到海水热含量月变化量的均方差,结果如图 2c所示.平均CTE的计算方法为:随深度不同分层计算热膨胀系数,并按深度的不同取加权平均[4, 20, 21].我们采用WOA05提供的气候态实测温盐场数据,利用该方法计算了平均CTE.比较图 2a~2c可以发现,在低纬度地区,表面CTE和平均CTE的结果差异相对较小,利用卫星测高得到的海水热含量变化与海洋模式得到的结果符合得较好.在中高纬度地区,方法二的结果较方法一明显改善.
3.3.4 利用卫星测高数据、OBP数据和平均CTE估计热含量变化(改进方法)在方法二的基础上,采用公式(11)对卫星测高得到的海平面变化进行OBP改正,再结合平均CTE计算得到海水热含量月变化量的均方差,结果如图 2d所示.与图 2c相比,改进方法的热含量估计在部分中高纬度地区改善明显.这些区域与图 1中OBP变化较大的区域是一致的.
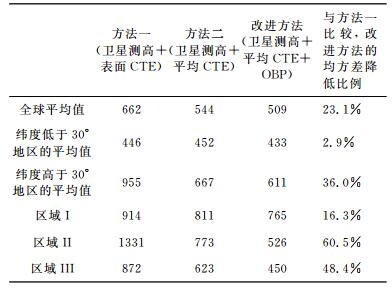
3.3.5 三种方法的统计结果比较选择低纬度地区(纬度低于30°)、中高纬度地区(纬度高于30°)、北太平洋区域Ⅰ(30°N~50°N,170°E~190°E)、南印度洋区域Ⅱ(40°S~60°S,100°E~120°E)和南太平洋区域Ⅲ(40°S~60°S,100°W~120°W)分别计算了海水热含量的月变化量,并与ECCO模式的结果比较,得到三种方法的均方差.如表 1所示,在中高纬度地区,改进方法的均方差较方法一降低了36.0%;在低纬度地区,改进效果不明显,均方差仅降低了2.9%;均方差的全球平均值降低了23.1%.在OBP变化较为明显的区域Ⅰ、区域Ⅱ和区域Ⅲ,改进方法的均方差分别降低了16.3%、60.5%和48.4%,估计精度明显提高.由于在中高纬度地区,采用表面CTE的方法一的结果较差,下文均采用了平均CTE进行热含量估计.
|
|
表 1 不同地区的海水热含量月变化量的均方差统计表(单位:l06 J/m2) Table 1 Statistical table of RMS of monthly heat content change in different areas (unit:106 J/m2) |
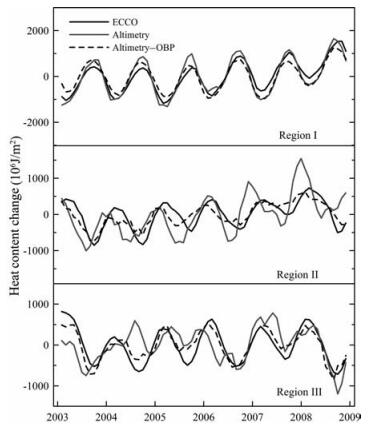
我们对上述3个区域在2003~2008年的热含量月平均变化量的时间序列进行了计算.从图 3的结果可以发现,考虑OBP改正后的结果与ECCO海洋模式的结果符合得更好.在改进较为明显的区域II和区域Ⅲ,其与ECCO结果的相关性分别为0.80和0.89;而没有考虑OBP的方法二与ECCO结果的相关性仅为0.49和0.45.因此,改进方法对提高中高纬度地区的热含量估计精度效果明显.
|
图 3 区域Ⅰ、区域Ⅱ和区域Ⅲ的海水热含量变化时间序列(2003~2008) Fig. 3 Time series of heat content change in Region Ⅰ、Region Ⅱ andRegion Ⅲ (2003~2008) |
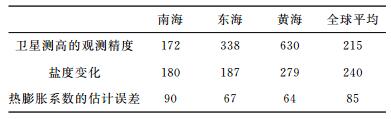
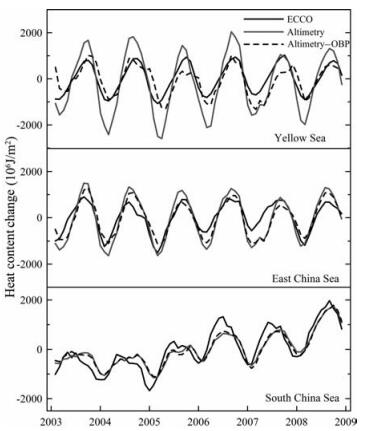
我们选择了南海(10°N~20°N,110°E~120°E)、东海(26°N~30°N,123°E~127°E)和黄海(30°N~34°N,123°E~127°E)的3个区域计算了海水热含量的变化,结果如图 4所示.从表 2的均方差统计结果来看,在3个计算区域,经过OBP改正后的均方差更小,即与ECCO模式的结果符合得更好.
|
图 4 南海、东海和黄海海水热含量变化时间序列(2003~2008) Fig. 4 Time series of heat content change in the South China Sea、the East China Sea and the Yellow Sea (2003~2008) |
|
|
表 2 中国近海海水热含量变化的统计表(单位:106 J/m2) Table 2 Statistical table of ocean heat content change in the China Sea (unit:106 J/m2) |
由于海水热含量变化具有强烈的周年变化特征,我们计算了3个区域热含量变化的周年项与半年项振幅.结果表明,考虑OBP变化的改进方法估计的周年项与ECCO模式的结果符合得更好.单纯利用测高数据估算的热含量周年项误差较大,特别是在东海和黄海海域,估计的周年项比ECCO的结果分别大1.6倍和2.0倍.这主要是因为东海和黄海都属于靠近大陆的浅海,除了受洋底压力变化影响外,高度计误差和海水盐度变化的影响也较大,导致热含量估计精度的降低.这在下一节将具体讨论.而南海大部分区域为深海区,卫星测高的精度较高,且盐度的影响较低,所以改进方法的结果与ECCO模式的结果符合得较好.除周年变化外,南海热含量还表现出明显的半年变化特征.这与佟景全等[5]的结果是一致的.
从图 4还可以看出,海水热含量的季节性变化比较明显.夏季的热含量较高,最大值一般出现在8、9月份;冬季的热含量较低,最小值出现在2、3月份.在南海,热含量变化还表现出一定的年际变化特征.ECCO模式的计算结果表明:南海在2003~2004年的海水热含量变化低于2003~2008年的平均值,2005~2006年海水热含量增加明显,2008年达到最大.方法二和改进方法的计算结果比较一致,主要表现为热含量增加的长期趋势.对三组时间序列进行线性拟合,ECCO模式计算的南海热含量长期变化为11.4 W/m2,方法二和改进方法的结果分别为9.2 W/m2和8.7 W/m2.模式与实测结果均表明,南海近年存在热含量增加的趋势.
3.5 全球及中国近海海水热含量变化的误差分析 3.5.1 卫星测高的精度测高卫星的轨道误差、高度计的观测噪声、反变气压计改正误差和潮汐模型误差等因素,都会影响卫星测高观测结果的精度,进而影响热含量的估计精度.本文利用AVISO提供的卫星测高观测值的误差数据,采用(12)式计算了卫星测高的观测精度对热含量估计的影响[8]
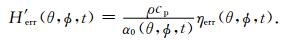
|
(12) |
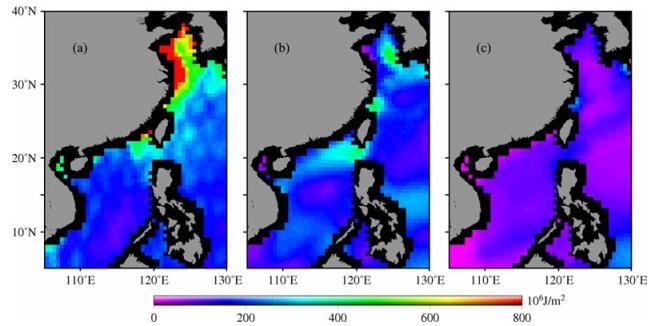
如图 5a所示,黄海和东海的卫星测高误差较大,由此引起的热含量估计误差也较大;南海大部分区域为深海区,卫星测高的精度较高,故引起的估计误差较小.表 3的统计结果也说明了这一点.
|
图 5 中国近海地区, (a)卫星测高的精度、(b)盐度变化和(c)热膨胀系数的估计误差对热含量估计的影响 Fig. 5 The effect of (a) satellite altimetry's accuracy, (b) salinity change and (c) thermal expansion coefficients' estimation error on heat content estimation in the China Sea |
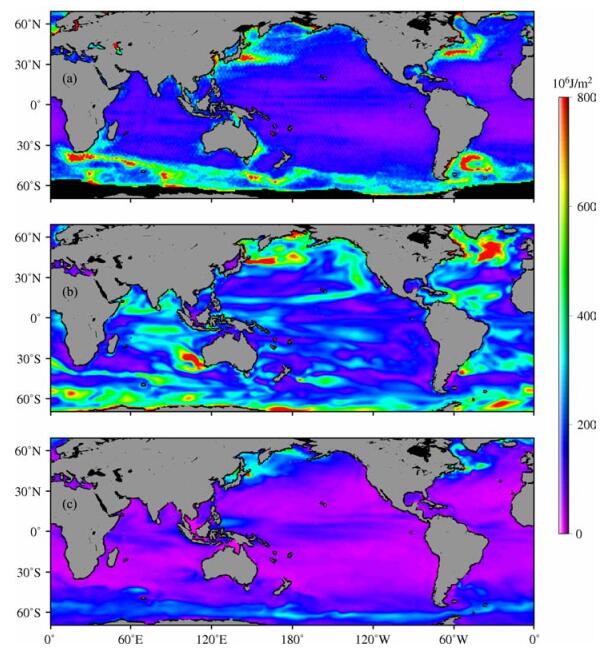
如图 6a所示,全球海洋地区,卫星测高的精度对热含量估计的影响主要来自高纬度地区.需要说明的是,AVISO提供的网格化测高数据在南极高纬度地区存在较多的数据空缺,因此在计算全球平均时,没有考虑这些地区的影响.
|
图 6 全球海洋地区, (a)卫星测高的精度、(b)盐度变化和(c)热膨胀系数的估计误差对热含量估计的影响 Fig. 6 The effect of (a) satellite altimetry's accuracy, (b) salinity change and (c) thermal expansion coefticients' estimation error on heat content estimation tn the global ocean |
早期的研究表明,部分沿海海域的盐度变化对热含量估计精度影响较大[20].本文利用ECCO三维温盐数据计算了盐度变化对海水热含量估计的影响.由于忽略盐度变化的影响而产生的估计误差可由下式表示[11]
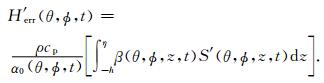
|
(13) |
如图 5b所示,黄海和东海的热含量估计受盐度变化的影响较大.因为在中国近海地区,受南海暖流、中国沿岸流、台湾暖流和黄海暖流等的影响以及江河淡水入海的影响,盐度的变化相对较大.而南海大部分区域为深海区,热含量估计受盐度变化的影响相对较小.具体统计结果见表 3.
|
|
表 3 卫星测高的精度、盐度变化和热膨胀系数的估计误差引起的误差的均方差(单位:l06 J/m2) Table 3 RMS of errors from satellite altimetry s accuracy, salinity change and thermal expansion coefficients, estimation error (unit:l06 J/m2) |
如图 6b所示,全球海洋地区,盐度变化对热含量估计的影响主要来自中高纬度地区,如南大洋、北太平洋西部和北大西洋等.这一方面是由于这些地区的盐度变化相对较大;另一方面是由于在高纬度地区,海水温度较低,海水的热膨胀系数较小,故热膨胀对热比容海平面变化的贡献变小,盐度膨胀的作用变得显著.在赤道区域,热膨胀系数在3×10-4 K-1左右;而在南北纬50°附近,热膨胀系数约为2×10-4 K-1;在更高纬度地区,热膨胀系数在1×10-4 K-1左右.由公式(13)可以看出,较小的热膨胀系数会导致较大的估计误差.因此,盐度变化是影响高纬度地区热含量估计精度的重要因素.在图 6b中,盐度变化对中低纬度地区的影响也较其他因素显著.经计算,盐度变化产生的热含量月变化量的均方差全球平均值为240×106 J/m2.
3.5.3 热膨胀系数的估计误差利用卫星测高估计海水热含量变化的传统方法中,热膨胀系数一般假定为与深度无关的常量,如公式(3)所示.实际上,随着深度的变化,热膨胀系数也会相应地改变.本文考虑了热膨胀系数随深度的变化,采用了分层计算取加权平均的方法估计了平均CTE.在估计高纬度地区热含量变化时,该方法较传统方法提高了估计精度,但仍存在估计误差.利用ECCO模式提供的时变三维温盐场数据,本文计算了热膨胀系数的估计误差对计算海水热含量的影响.计算公式为[11]
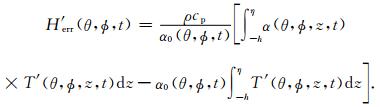
|
(14) |
如图 5c所示,东海和黄海的热含量估计受热膨胀系数的估计误差的影响较小,而南海区域的影响略大.这主要是因为,东海和黄海属于浅海,海水热膨胀系数的变化较小,将其作为常数引起的误差也较小.而南海大部分海域为深海区,热膨胀系数随深度的不同变化明显,故其引起的热含量估计误差略大.统计结果见表 3.
如图 6c所示,全球海洋地区,热膨胀系数的估计误差对热含量估计的影响主要也表现在中高纬度地区.如表 3所示,由此引起的均方差全球平均值为85×106 J/m2,较盐度变化引起的估计误差小了近1/3.
4 结论与展望本文联合卫星测高和洋底压力数据,计算了全球和中国近海的海水热含量变化,并与传统方法和ECCO海洋模式数据的计算结果进行了比较,通过分析得到如下初步结论:
(1) 在低纬度地区,海平面变化主要是由于海水热膨胀导致的.故单纯利用卫星测高技术得到的热含量变化在低纬度地区是可靠的.在OBP变化较大的中高纬度地区,联合卫星测高、OBP数据和平均CTE的改进方法提高了海水热含量的估计精度.在南北纬30°以上地区,改进方法的估计精度提高了约36.0%;对部分OBP变化较大的区域,估计精度提高了60%以上.
(2) 在中国近海区域,考虑OBP变化的改进方法也在一定程度上提高了海水热含量的估计精度.计算结果表明,东海和黄海的海水热含量变化主要表现为明显的周年变化特征,而南海区域还存在半年项和年际项变化特征,且近年存在明显的热含量增加的趋势.
(3) 全球海洋地区,盐度变化和卫星测高的精度是影响中高纬度地区热含量估计精度的重要因素.在中国近海区域,卫星测高的精度和盐度变化对东海和黄海的热含量估计影响较大,对南海的热含量估计影响相对较小.
(4) 热膨胀系数的估计误差对热含量估计的影响主要表现在中高纬度地区.在中国近海区域,由此带来的影响相对较小.
目前,利用GRACE卫星重力方法获得的洋底压力数据的时空分辨率仍相对较低.随着卫星重力技术及其数据处理方法的不断进步,有望联合卫星测高和卫星重力两种独立的卫星观测手段,获得中长波长高精度的海水热含量变化信息.有关联合两种卫星观测手段计算海水热含量的工作进展,将在另文报告.另外,随着Argo等全球性海洋温盐观测系统的不断完善,通过实测温盐资料有望获得高精度的海水热含量信息,也将进一步加深人们对全球和区域海水热含量变化规律的理解.
致谢感谢法国AVISO提供了测高数据、美国JPL提供了ECCO海洋模式数据和美国NOAA提供了WOA05数据.文中图片是用GMT[22]软件生成的.
| [1] | Gill A E, Niiler P P. The theory of seasonal variability in ocean. Deep Sea Res. , 1973, 20(2): 141-177. |
| [2] | Rebert J P, Donguy J R, Eldin G, et al. Relations between sea level, thermocline depth, heat content, and dynamic height in the tropical Pacific ocean. J.Geophys.Res. , 1985, 90(NC6): 1719-1725. |
| [3] | Chen J L, Shum C K, Wilson C R, et al. Seasonal sea level change from TOPEX/Poseidon observation and thermal contribution. J.Geod. , 2000, 73(12): 638-647. DOI:10.1007/s001900050002 |
| [4] | Chambers D P, Tapley B D, Stewart R H. Measuring heat storage changes in the equatorial Pacific:a comparison between TOPEX altimetry and tropical atmosphere-ocean buoys. J.Geophys.Res. , 1998, 103(C9): 18591-18597. DOI:10.1029/98JC01683 |
| [5] | 佟景全, 王静, 齐义泉. 基于卫星高度计资料分析南海热含量的年际变化特征. 地球物理学报 , 2006, 49(6): 1651–1656. Tong J Q, Wang J, Qi Y Q. Interannual variability of the heat storage anomaly in the South China Sea estimated from merged altimetric data. Chinese J.Geophys. (in Chinese) , 2006, 49(6): 1651-1656. DOI:10.1002/cjg2.v49.6 |
| [6] | Wada A, Chan J C L. Relationship between typhoon activity and upper ocean heat content. Geophys.Res.Lett. , 2008, 35: L17603. DOI:10.1029/2008GL035129 |
| [7] | Yan X H, Niiler P P, Nadiga S K, et al. Seasonal heat-storage in the North Pacific:1976-1989. J.Geophys.Res. , 1995, 100(C4): 6899-6926. DOI:10.1029/94JC03230 |
| [8] | Chambers D P, Tapley B D, Stewart R H. Long-period ocean heat storage rates and basin-scale heat fluxes from TOPEX. J.Geophys.Res. , 1997, 102(C5): 10525-10533. DOI:10.1029/96JC03644 |
| [9] | White W B, Tai C K. Inferring interannual changes in global upper ocean heat storage from TOPEX altimetry. J.Geophys.Res. , 1995, 100(C12): 24943-24954. DOI:10.1029/95JC02332 |
| [10] | Wang L P, Koblinsky C. Can the Topex/Poseidon altimetry data be used to estimate air-sea heat flux in the North Atlantic?. Geophys. Res. Lett. , 1997, 24(2): 139-142. DOI:10.1029/96GL03695 |
| [11] | Jayne S R, Wahr J M, Bryan F O. Observing ocean heat content using satellite gravity and altimetry. J.Geophys.Res. , 2003, 108(C2): 3031. DOI:10.1029/2002JC001619 |
| [12] | Wyrtki K, Uhrich L. On the accuracy of heat-storage computations. J.Phys.Oceanogr. , 1982, 12(12): 1411-1416. DOI:10.1175/1520-0485(1982)012<1411:OTAOHS>2.0.CO;2 |
| [13] | United Nations Educational, Scientific, and Cultural Organization (UNESCO).Tenth report of the joint panel on oceanographic tables and standards.UNESCO CTEh.Pap.Mar.Sci., 1981.17~19 |
| [14] | 吉尔A E.大气-海洋动力学.张立政等译.北京:海洋出版社, 1988.470~471 Gill A E.Atmosphere-Ocean Dynamics (in Chinese).Translated by Zhang L Z, et al.Beijing:Ocean Press, 1988.470~471 |
| [15] | Ponte R M. Variability in a homogeneous global ocean forced by barometric pressure. Dynamics of Atmospheres and Oceans , 1993, 18(3-4): 209-234. DOI:10.1016/0377-0265(93)90010-5 |
| [16] | Tomczak M, Godfrey J. Regional Oceanography:An Introduction. New York: Pergamon, 1994 . |
| [17] | Ducet N, Le Traon P, Reverdin G.Global high-resolution mapping of ocean circulation from TOPEX/Poseidon and ERS-1 and-2.J.Geophys.Res., 105(C8):19477~19498 |
| [18] | Locarnini R, Mishonov A, Antonov J, et al.World Ocean Atlas 2005, Volume l:Temperature.In:Levitus S ed.NOAA Atlas NESDIS.Washington, D.C.U.S.Gov, Printing Office, 2006 |
| [19] | Antonov J, Locarnini R, Boyer T, et al.World Ocean Atlas 2005, Volume 2:Salinity.In:Levitus S ed.NOAA Atlas NESDIS.Washington, D.C.:U.S.Gov.Printing Office, 2006 |
| [20] | Sato O T, Polito P S, Liu W T. Importance of salinity measurements in the heat storage estimation from TOPEX/POSEIDON. Geophys.Res.Len. , 2000, 27(4): 549. DOI:10.1029/1999GL011003 |
| [21] | Willis J K, Roemmich D, Cornuelle B. Interannual variability in upper ocean heat content, temperature, and thermosteric expansion on global scales. J.Geophys.Res. , 2004, 109(C12036). DOI:10.1029/2003JC002260 |
| [22] | Wessel P, Smith W. Free software helps map and display data. Eos Trans.AGU , 1991, 72(41): 441. |
 2010, Vol. 53
2010, Vol. 53