2. 武汉大学地球空间环境与大地测量教育部重点实验室, 武汉 430079;
3. 中国地震局地震研究所, 武汉 430071
2. Key Laboratory of Geospace Environment and Geodesy, Ministry of Education, Wuhan University, Wuhan 430079, China;
3. Institute of Seismology, CEA, Wuhan 430071, China
由于GPS技术具有精度高、覆盖好、成本低等优点, 越来越多的低轨对地观测卫星包括CHAMP、GRACE、ICESat、Janson等开始搭载GPS接收机作为其主要的精密定轨跟踪技术.而随着星载GPS接收机性能的提高以及星载GPS观测数据处理方法的完善, 基于GPS技术的精密定轨方法逐渐成为精密定轨中的研究热点[1].
利用GPS技术的精密定轨本质上是个参数估计问题, 为了获得高精度的精密定轨结果, 不仅要利用正确的函数模型, 而且也要采用合理的随机模型.在过去的十几年里, 国内外学者在GPS观测模型(函数模型)方面做了大量研究, 提出并发展了包括非差模型、历元间单差模型、星间单差模型、联合地面观测数据的双差模型等函数模型[1~4].然而在低轨卫星精密定轨随机模型方面, 仍然广泛采用适合于地面观测数据的随机模型[5], 主要包括高度角和载噪比模型[6].许多研究表明卫星高度角与观测值噪声存在函数关系, 因此已被广泛应用于地面观测数据的噪声描述中, 现在许多科学和商业GPS数据处理软件均采用高度角加权随机模型[7].载噪比(C/N0)是载波信号功率与噪声功率在1Hz带宽上的比值, 是信噪比的归一化度量[8].Brunner等基于C/N0建立了SIGMA-ε模型[8]和SIGMA-Δ模型[9], 实际数据分析表明, 基于载噪比的随机模型能很好地削弱多路径效应的影响.
虽然高度角随机模型和载噪比随机模型已经在地面GPS观测数据处理中得到了广泛应用并取得了可靠的结果, 然而上述模型对星载GPS观测数据, 特别是对类似于GRACE卫星的超低轨道对地观测卫星来说是否合适, 还需要做详细分析和评估.本文将首先分析GRACE卫星GPS实测数据的特点, 在此基础上给出适合星载GPS观测值噪声分布的扩展高度角随机模型和载噪比随机模型.进而通过对GRACE卫星进行非差运动学定轨, 对提出的扩展随机模型进行评估, 旨在为确定适合星载GPS观测数据的随机模型, 并为提高精密定轨精度提供依据.
2 星载GPS观测值噪声分析为了确定适合星载GPS观测值的随机模型, 应首先分析星载GPS观测值的噪声分布特点.由于缺乏参考, 星载GPS数据的噪声分析不能采用地面观测值分析中的“零基线法”, 而只能借助于观测独立的码观测值和载波相位观测值[10].噪声分析时采用的观测数据来自于GRACE卫星2008年8月1日至3日的星载GPS观测数据, 采用的精密轨道是利用作者自主开发的精密定轨软件计算得到的.
2.1 码观测值噪声若多路径组合公式中的多路径误差为零[10], 则可以被用来分析码观测值的噪声水平, 对GRACE卫星实测数据的分析表明, 多路径和系统误差仅发生在相对于星固坐标系的后半球内[11], 因此可以利用前半球内的卫星观测值来分析观测值的噪声水平.噪声分析的主要步骤为, 首先利用有效的周跳和粗差探测方法[12], 剔除观测数据中的粗差并探测周跳, 然后根据周跳将观测数据分成多个不同的观测弧段, 之后计算每个弧段的偏差值, 进而计算出每个观测值的噪声, 最后根据观测噪声拟合得到观测值噪声的分布函数.为了合理地解释观测值噪声, 可以将其表示为载噪比的函数.载噪比与信噪比的关系如下[10]:
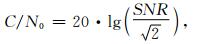
|
(1) |
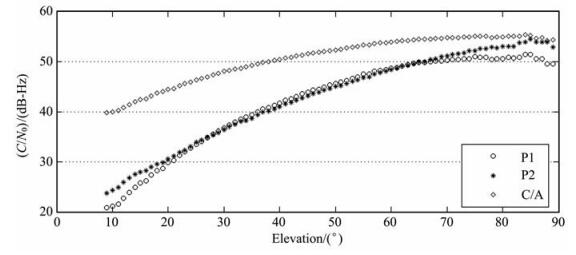
其中, SNR是RINEX观测文件中提供的码观测值对应的信噪比.载噪比与高度角强相关, 图 1给出了码观测值载噪比随高度角的变化情况, 由图可知, C/A码的载噪比在10°高度角处约为40 dB-Hz, 在天顶方向约为55 dB-Hz; 而P1和P2码载噪比的变化范围为20 dB-Hz至55 dB-Hz, 这是利用半无码跟踪技术跟踪P码时信号平方引起的[10].
|
图 1 载噪比相对于高度角的变化 Fig. 1 The variation of C/N0 corresponding to elevation |
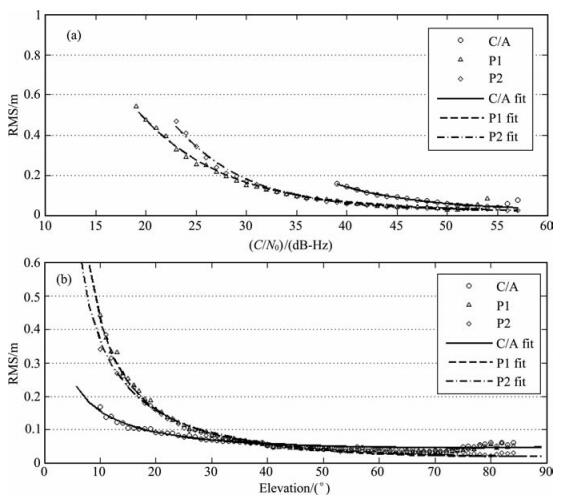
为了全面分析码观测值噪声变化情况, 图 2a给出了2008年8月1日至3日的码观测值噪声RMS相对于C/N0的变化情况.图 2b给出了码观测值噪声相对于高度角的变化图.
|
图 2 码观测值噪声相对于载噪比(a)和相对于高度角(b)变化 Fig. 2 The variation of code measurement noise corresponding to C/N0 (a) and elevation (b) |
图 2a表明, C/A码的噪声在55 dB-Hz处达到最小值5 cm, 在38 dB-Hz处达到最大值20 cm.P1和P2码的噪声在50 dB-Hz处达最小值5 cm.P1码在19 dB-Hz处噪声值为55 cm, P2码在23dB-Hz处的噪声为48 cm.此外, P2码的噪声整体上比P1码的大, 产生这种现象的具体原因还不清楚.由图 2b可以看出, 在高度角40°~90°之间, 三个码观测值的噪声均非常小, 约为5 cm左右.从40°开始, 随着高度角的降低, 码观测值噪声随之增大, 但是三种码观测值的噪声变化并不相同, 其中C/A码相对变化较小, 精度较高, 而P1码和P2码变化较快, 精度较差.
2.2 载波相位观测值噪声BlackJack星载GPS接收机的观测数据中, 在频率L1上有两个独立的观测值, 即L1和LA观测值, 它们分别是由C/A码和P1码的跟踪信道观测得到的.由于L1和LA观测值的误差影响是相同的, 因此两者的差值在每个弧段内都在某一常数附近波动, 可以用来评估载波相位观测值的噪声水平.两者差值的标准偏差的关系为
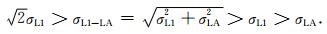
|
(2) |
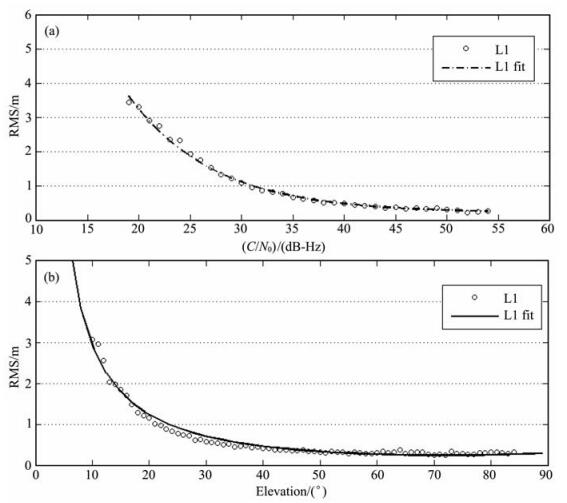
上式给出了L1和LA载波相位观测值噪声的上下限值.由于在提取P1码观测值时采用了半无码跟踪技术, 因此L1的噪声比LA的噪声大.所以σL1-LA可以认为是L1载波相位观测值精度的近似.图 3a给出了2008年8月1日L1观测值噪声相对于载噪比的变化图, 可见, L1与LA差值的标准偏差在高载噪比处的噪声约为0.5 mm, 在低载噪比处时精度最差可达3.5 mm.
3 改进的随机模型目前广泛应用的随机模型主要有四类, 即等权随机模型、基于验后残差的随机模型、基于高度角的随机模型以及基于载噪比的随机模型.基于高度角和载噪比的加权方法不仅模型简单而且能够较好地反映观测值的质量状况, 因而得到了广泛应用[6].
3.1 扩展的高度角随机模型高度角随机模型将观测值噪声σ表达为高度角的函数, 即
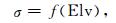
|
(3) |
其中, Elv为高度角.这类函数主要有指数函数模型, 正弦函数模型以及余弦函数模型等, 其中最常用的模型为正弦模型:

|
(4) |
上述函数模型已经广泛应用于静态和动态精密定位中, 但是对GRACE卫星实测数据的分析表明, 上述随机模型不能准确地描述观测值噪声随着高度角的变化情况.为此, 本文提出了扩展的正弦随机模型:

|
(5) |
式中, a, b, c, d为待定系数, 可以根据实测数据分析确定.根据2008年8月1日至3日GPS观测值的噪声变化, 拟合得到了码观测值噪声(C1、P1和P2)和载波相位观测值噪声(φ1)的扩展的正弦随机模型, 分别为:
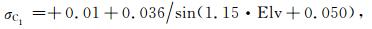
|
(6) |

|
(7) |
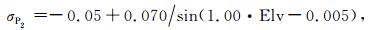
|
(8) |
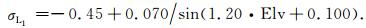
|
(9) |
相应拟合残差的标准差分别为0.68 cm、1.11 cm、1.03 cm和0.60 mm (图 2b、图 3b), 由此可知, 扩展的正弦模型能够很好地拟合观测值噪声变化.
|
图 3 L1观测噪声相对于载噪比(a)和相对于高度角(b)的变化 Fig. 3 The variation of L1 measurement noise corresponding to C/N0(a) and elevation (b) |
载噪比C/N0是载波信号能量与噪声能量在1Hz带宽上的比值, 它与多路径效应、接收机天线增益、天线电缆的衰减、卫星信号发射水平以及对流层延迟等有关.Langley的研究表明载噪比是描述GPS接收机性能的重要参数并且能够直接反映观测值的精度水平[13].Brunner等利用C/N0观测值建立了载波相位观测值的SIGMA-ε随机模型[9], 即:

|
(10) |
其中, σφ2为非差载波相位方差(单位m2); Ci=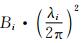
在利用上述模型对GRACE卫星载波相位观测值噪声进行分析时发现, 上述模型也不能够准确恰当地描述载波相位观测值噪声的变化, 为此将上述模型扩展为:

|
(11) |
其中, V、a和b为待定参数, 其他参数含义与公式相同, 利用上述模型对载波相位φ1的噪声进行拟合, 得到的拟合函数为:
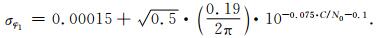
|
(12) |
由图 3a可见, 扩展的拟合函数能够非常好地拟合φ1观测值噪声(拟合残差的标准差为0.92 mm), 因此更适用于GRACE卫星精密定轨.
与上述载波相位的随机模型相似, 扩展的码观测值载噪比随机模型为[14]
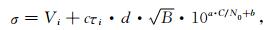
|
(13) |
式中τi为码元宽度(单位为s), d=0.1(chip)为相关器宽度, 其他符号与前式相同.对GRACE卫星GPS码观测值噪声进行分析, 拟合得到码观测值随机模型分别为:

|
(14) |

|
(15) |
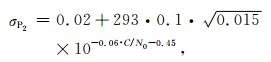
|
(16) |
上述随机模型对观测值噪声的拟合情况如图 2a所示(拟合残差的标准差分别为0.99 cm、1.24 cm和0.98 cm), 可见上述随机模型能很好地描述码观测值噪声.
4 非差运动学精密定轨在分析不同随机模型对精密定轨的影响时, 本文采用基于最小二乘批处理算法的非差运动学方法, 需要估计的参数包括每个历元3个卫星坐标、1个低轨卫星接收机钟差, 还包括所有的与观测弧段相关的非差模糊度参数, 此时模糊度不再具有整数特性.采用的函数模型、随机模型, 以及一些特殊的模型改正, 如GPS卫星天线相位中心偏差改正、相位缠绕改正、相对论效应改正, 低轨卫星的相位中心偏差改正、相位缠绕改正、相对论效应改正, 地球自转改正等相关参数如表 1所示.需注意的是, 由于GRACE卫星的飞行高度在450 km左右, 因此其不受对流层的影响.在非差运动学定轨中, 所有的坐标转换参数均与IERS2003的规范相一致, 提供的低轨卫星轨道包括ITRF坐标系和卫星轨道坐标系两套坐标系下的坐标.在计算低轨卫星相位中心相对于质量中心的坐标改正时所需要的空间姿态角由恒星敏感器测得.
|
|
表 1 非差运动学精密定轨相关参数 Table 1 Related parameter in zero-difference kinematic orbit determination |
对于1天的GRACE卫星观测数据, 非差运动学精密定轨要处理的参数高达3万多个.为了加快数据处理速度, 在软件设计中采用了快速算法, 即首先消去所有的历元参数, 进而得到仅包含弧段参数(模糊度参数)的法方程, 然后将其求逆后回代, 最后得到所有的历元参数解[13, 15].
5 随机模型对精密定轨的影响分析 5.1 算例说明在分析随机模型对精密定轨的影响时, 采用的随机模型有四种:(1)高度角随机模型; (2)扩展的高度角随机模型; (3)载噪比随机模型; (4)扩展的载噪比随机模型.其中模型(2)和模型(4)为本文提出的新模型.需要注意的是, 由于利用GRACE卫星GPS观测数据只能分析出φ1载波相位的随机模型, 而非差运动学精密定轨中的观测模型为φ1和φ2无电离层组合模型, 因此在软件中假设φ1和φ2载波相位的随机模型是相同的.在分析上述随机模型时采用的GPS观测数据为2008年1月1日GRACE卫星的GPS观测数据, 在精密定轨时采用的精密星历和钟差为CODE分析中心的事后精密星历和5s间隔的精密钟差产品.采用的参考轨道为JPL提供的事后精密轨道, 其标称精度优于5 cm[16].
5.2 数值分析利用非差运动学定轨方法, 分别采用上述四种随机模型, 对2008年8月1日的GRACE-A卫星进行了轨道计算, 将其与JPL提供的精密轨道进行比较分析, 得到的非差运动学轨道精度如表 2所示.可见, 扩展的高度角模型比传统的高度角模型精度略有提高.传统的载噪比模型的精度相对较差, 径向精度仅为4.9 cm, 说明传统载噪比模型并不能有效地描述观测值的随机特性, 而扩展的载噪比模型的定轨精度有明显提高, 其径向定轨精度达到了3.4 cm, 说明扩展的载噪比模型能较好地描述GRACE卫星的观测值噪声情况.
|
|
表 2 不同随机模型对应的运动学定轨精度(单位:cm) Table 2 Kinematic orbit accuracy for different stochastic model (cm) |
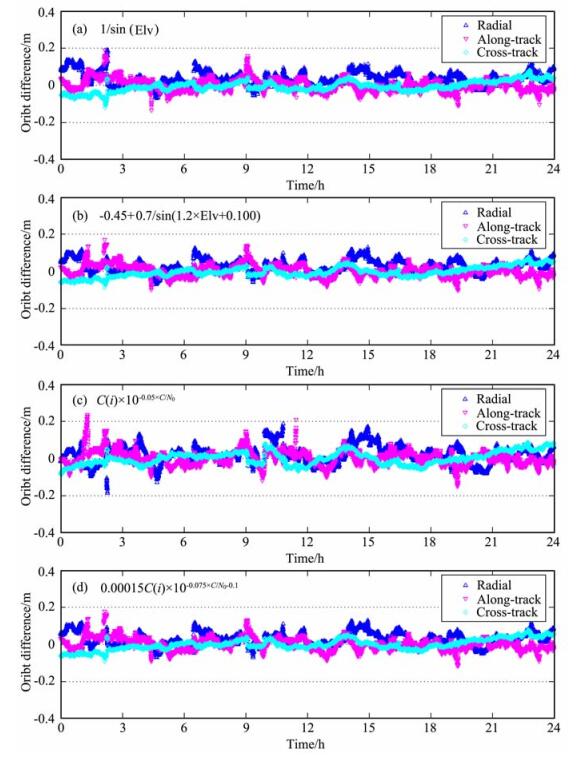
图 4(a~d)分别给出了四种随机模型对应的运动学轨道差值变化, 可见, 扩展的高度角随机模型和扩展的载噪比随机模型能够一定程度上抑制轨道的异常变化, 因此定轨精度比传统模型的高.
|
图 4 不同随机模型对应的运动学轨道差值 (a)髙度角随机模型; (b)扩展的髙度角模型; (c)载噪比随机模型; (d)扩展的载噪比随机模型. Fig. 4 Kinematic orbit difference with JPL reference orbit for different stochastic model (a) Elevation-dependentmodel; (b) Extended elevation-dependent model; (c) C/N0-derived model (d) Extended C/N0-derived model. |
本文在分析GRACE卫星实测GPS观测值噪声分布的基础上, 提出了扩展的高度角模型和扩展的信噪比模型, 并利用自主开发的精密定轨软件采用非差运动学定轨方法, 比较分析了四种不同随机模型(高度角随机模型、扩展的高度角随机模型、载噪比随机模型、扩展的载噪比随机模型)的非差运动学定轨精度.通过与JPL提供的事后精密科学轨道的比较得到了如下结论:
(1) 传统的高度角模型的运动学轨道径向精度为3.4 cm, 扩展的高度角模型的为3.3 cm, 后者比前者精度略有提高;
(2) 传统的载噪比模型的运动学径向精度为4.9 cm, 扩展的载噪比模型的为3.4 cm, 精度提高达1.5 cm, 说明扩展的载噪比模型能较好地描述GRACE卫星的观测值噪声变化特点;
(3) 扩展的高度角随机模型和扩展的载噪比随机模型相比传统的模型均能够在一定程度上抑制轨道的异常变化, 因此定轨精度也均比传统模型的好.
| [1] | ŠvehlaD, RothacherM. Kinematic and reduced-dynamic precise orbit determination of low earth orbiters. Advances in Geosciences , 2002, 1: 1–10. |
| [2] | Bisnath S B, Langley R B.Precise orbit determination of low earth orbiters with GPS point positioning.Proceedings of The Institute of Navigation 2001 National Technical Meeting, Long Beach, CA, U.S.A., 2001.725~733 |
| [3] | Bock H, Hugentobler U, Beutler G.Kinematic Orbit determination for Low Earth Orbiters (LEOs).In:Adam J, Schwarz K P, Editors.IAG 2001 Scientific Assembly, Vistas for Geodesy in the New Millenium.Springer IAG, Budapest, 2001.322~328 |
| [4] | Montenbruck O, Gill E, Kroes R. Rapid orbit determination of LEO satellites using IGS clock and ephemeris products. GPS Solutions , 2005, 9(3): 226-235. DOI:10.1007/s10291-005-0131-0 |
| [5] | Švehla D, Rothacher M.Kinematic orbit determination of LEOs based on zero-or double-difference algorithms using simulated and real SST data.In:Adam J, Schwarz K P Eds.IAG 2001 Scientific Assembly, Budapest, Vistas for Geodesy in the New Millenium.Springer, 2002.322~328 |
| [6] | 戴吾蛟, 丁晓利, 朱建军. 基于观测值质量指标的GPS观测量随机模型分析. 武汉大学学报(信息科学版) , 2008, 33(7): 718–722. Dai W J, Ding X L, Zhu J J. Comparing GPS stochastic models based on observation quality indices. Geomatics and Information Science of Wuhan University (in Chinese) , 2008, 33(7): 718-722. |
| [7] | Teferle F N, Orliac E J, Bingley R M. An assessment of Bernese GPS software precise point positioning using IGS final products for global site velocities. GPS Solutions , 2007, 11(3): 205-213. DOI:10.1007/s10291-006-0051-7 |
| [8] | Wieser A, Brunner F K. An extended weight model for GPS phase observations. Earth Planets Space , 2000, 52: 777-782. DOI:10.1186/BF03352281 |
| [9] | Brunner F K, Hartinger K H, Troyer L. GPS signal diffraction modeling:the stochastic SIGMA-Δ model. Journal of Geodesy , 1999, 73: 259-267. DOI:10.1007/s001900050242 |
| [10] | Montenbruck O, Kroes R. In-flight performance analysis of the CHAMP BlackJack GPS Receiver. GPS Solutions , 2003, 7(2): 74-86. DOI:10.1007/s10291-003-0055-5 |
| [11] | Kroes R.Precise relative positioning of formation flying spacecraft using GPS[Ph. D. thesis].Delft, the Netherlands, 2006 |
| [12] | 李建成, 张守建, 邹贤才, 等. GRACE卫星非差运动学厘米级定轨. 科学通报 , 2010, 55(7): 600–606. Li J C, Zhang S J, Zou X C, et al. Precise orbit determination for GRACE with zero-difference kinematic method. Chinese Science Bulletin (in Chinese) , 2010, 55(7): 600-606. DOI:10.1007/s11434-009-0286-0 |
| [13] | Langley R. GPS receiver noise. GPS World , 1997, 8: 40-45. |
| [14] | Montenbruck O.Preflight Validation of the MosaicGNSS GPS Receiver for TerraSAR-X.DLR-GSOC GTN-TST-0210.Deutsches Zentrum für Luft-und Raumfahrt, Oberpfaffenhofen, 2005 |
| [15] | 邹贤才. 卫星轨道理论与地球重力场模型的确定. 武汉: 武汉大学, 2007 . Zou X C. Theory of satellite orbit and earth gravity field determination (in Chinese). Wuhan: Wuhan University, 2007 . |
| [16] | Montenbruck O, Gill E, Kroes R. Rapid orbit determination of LEO satellites using IGS clock and ephemeris products. GPS Solutions , 2005, 9(3): 226-235. DOI:10.1007/s10291-005-0131-0 |
 2010, Vol. 53
2010, Vol. 53




