地球物理学报  2010, Vol. 53 Issue (6): 1495-1501   PDF    
引用本文
牛滨华, 孙春岩, 闫国英 等. 含气介质临界点、流体和骨架弹性参数的数值计算方法. 地球物理学报, 2010, 53(6): 1495-1501, doi: 10.3969/j.issn.0001-5733.2010.06.027.  
Niu B H, Sun C Y, Yan G Y, et al. Numerical calculation method for getting critical point, pore fluid and framework parameters of gas-bearing media. Chinese J. Geophys. (in Chinese), 2010, 53(6): 1495-1501, doi: 10.3969/j.issn.0001-5733.2010.06.027.  
含气介质临界点、流体和骨架弹性参数的数值计算方法
牛滨华 , 孙春岩 , 闫国英 , 杨维 , 刘畅     
中国地质大学(北京)地球物理与信息技术学院, 北京 100083
收稿日期 2009-07-13, 2010-05-17 收修定稿
基金项目: 国家自然科学基金(40874052)和中国地质大学(北京)地下信息探测技术与仪器教育部重点实验室资助
作者简介: 牛滨华, 男, 1952年生, 博士, 现为中国地质大学(北京)地球物理与信息技术学院教授, 多年从事地球物理的教学与科研工作; 中国地球物理学会终生会员, 中国地质学会会员, 美国SEG Active Member.E-mail:niubh1@cugb.edu.cn
摘要: 目前临界孔隙度及孔隙介质的研究主要为测试分析的实验方法，如何运用数值计算方法求取孔隙流体介质临界点和组分弹性参数一直是备受关注的课题.本文提出了求取孔隙介质临界点、孔隙内流体和骨架弹性参数的数值计算公式及方法，并结合含气样品测试数据实现了这种数值计算.文章首先给出了3个包含孔隙度的线性方程，通过有机组合每个线性方程中的两个系数得到求取有关弹性参数的数值计算公式.然后，详细阐述了计算的方法和步骤以及需要注意的问题，把室内含气砂岩样品实测的综合介质密度、纵波速度和横波速度作为数值计算的输入数据，求得了临界点和流体及骨架等相关弹性参数的具体数值.通过比较分析本文数学方法求得的计算数据与实验方法测得的实测数据，表明了该数值计算公式的正确性和数值实现方法的有效性.
关键词: 数值计算      含气孔隙介质      临界点及流体和骨架      弹性参数     
Numerical calculation method for getting critical point, pore fluid and framework parameters of gas-bearing media
NIU Bin-Hua, SUN Chun-Yan, YAN Guo-Ying, YANG Wei, LIU Chang     
School of Geophysics and Information Technology, China University of Geosciences (Beijing), Beijing 100083, China
Abstract: The mostly used methods for studying critical porosity and porous media are experimental measurement and analysis of testing data, and how to determine the porosity at critical point and the constituents' parameters are also topics of great concern. In this article, we provide a method for calculation of these elastic parameters. In the beginning, we derive three linear equations for numerical calculation. By combining regression coefficients of the equations, we propose equations for calculating constituents' parameters. After that we elaborate on the steps for calculation and give some notes. Then we use our method to analyze gas-bearing sandstone samples. In the process, let entire densities, P-velocities and S-velocities as input data, we calculate relative parameters about pore fluid, framework and critical point. In the end, by comparing the results with test data of experiment measurement, we test our method and it is proved to be successful..
Key words: Numerical calculation      Gas-bearing porous media      Critical point      pore fluid and framework      Elastic parameters     
1 引言

含孔隙流体介质的研究始终是岩石物理学和勘探地震学，特别是石油天然气产业部门等领域的重要课题[1~7].Amos Nur、Gary Mavko、Jack Dvorkin和Chen Qiang (1991~1998)等人通过测试分析岩石样品的实验方法，提出了临界孔隙度的概念和临界孔隙介质[1~4].这项工作拓宽了孔隙流体介质研究的思路和方法，有助于人们深入地认识和理解孔隙流体介质的构造及演化.

临界孔隙度是一个重要参数，其数值取决于岩石的内部结构和外部环境.Nur等人[2~4]通过对样品测试分析的实验方法，结合前人工作成果，给出了砂岩、白云岩、浮石和裂缝火成岩等岩石的临界孔隙度数值.由此表明临界孔隙度是以隐性方式存在于介质内部的，同时也告诉人们可以通过实验方法得到临界孔隙度.

首先通过实验方法获得整体孔隙介质密度、横波和纵波速度，然后应用数值计算分析方法求取介质中临界度、孔隙内流体和骨架弹性参数，这是一个在理论和应用方面均很有意义的研究课题.这项工作可以丰富和发展孔隙流体介质数值计算及分析的方法，也能为孔隙介质流体属性的识别和分析提供新的途径.但是至目前为止，几乎未见到关于临界孔隙介质“数值计算求取临界点和流体及骨架弹性参数”方面的报道，本文基于Nur (1998)[2]和Chen (1994)[4]等人关于临界孔隙介质的工作，提出了求取孔隙介质临界点、孔隙内流体和骨架弹性参数的数值计算公式及方法，并结合含气样品测试数据实现了这种数值计算.

本文首先给出3个线性方程:孔隙度φ和密度ρ，孔隙度φ和ρVS2即密度与横波速度平方的乘积，孔隙度φ和ρVP2即密度与纵波速度平方的乘积；然后，详细阐述了数值计算的步骤和实现方法以及需要注意的问题.结合美国劳伦斯-利物莫国家实验室的含气砂岩样品的测试数据[5]，把测试的含气综合介质体密度、纵波速度和横波速度作为数值计算的输入数据，运用数值计算公式和方法求取了临界点的密度、体积模量和速度，流体的密度、体积模量和速度，骨架的密度、体积及剪切模量、纵横波速度等弹性参数的具体数值.最后，把数学方法的计算数据与实验方法的测试数据进行了比较分析，证实了本文数值计算公式的有效性.

2 孔隙介质的线性方程

密度、剪切和体积模量方程是各向同性均匀弹性临界孔隙流体介质的3个基本公式[2, 4].

综合介质的体密度方程为

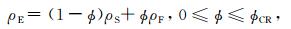
(1)

式中，ρE、ρS和ρF分别是综合介质、骨架固体和孔隙流体的体密度(简称密度)；φ是综合介质的孔隙度；φCR是临界点孔隙度.

综合介质的剪切模量方程是

(2)

式中μE和μS分别是综合介质和骨架的剪切模量.

综合介质的体积模量方程为

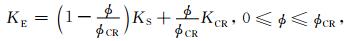
(3a)

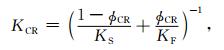
(3b)

其中，KE、KS和KCR分别是综合介质、骨架和临界点的体积模量；KF是流体的体积模量.

综上，各向同性均匀弹性临界孔隙流体介质有4个基本参数，它们分别是综合介质的密度、剪切和体积模量以及临界点孔隙度.

基于(1)至(3)式，综合孔隙介质的横波速度VES和纵波速度VEP分别为

(4)

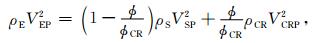
(5)

其中，骨架、临界点和流体的纵波速度即VSP、VCRP和VFP以及骨架的横波速度VSS分别为

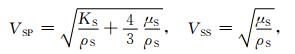
(6)

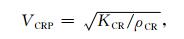
(7)

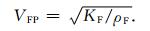
(8)

3 数值计算公式

用于数值计算的公式包含如下几部分，下面分别叙述之.

(Ⅰ)孔隙度与密度的线性方程.

式(1)可以等价地写成如下线性方程:

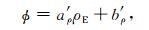
(9a)

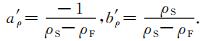
(9b)

依据观测的综合介质密度ρE(φ)，运用最小二乘法拟合确定直线方程(9a)式及(9b)式a′ρ和b′ρ系数.得到骨架和流体的密度ρS和ρF分别为

(10)

(Ⅱ)孔隙度与密度-横波速度平方的线性方程.式(4)可以等价地写成如下线性方程:

(11a)

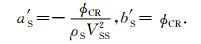
(11b)

根据实验得到的综合介质的横波速度VES(φ)和密度ρE(φ)，应用最小二乘法拟合确定直线方程(11a)式及(11b)式a′S和b′S系数.于是临界点孔隙度φCR和骨架横波速度VSS分别为

(12)

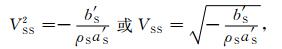
(13)

其中ρS由(10)式求出.

运用密度组分方程(1)可以求出临界点孔隙度φCR对应的密度ρCR，即

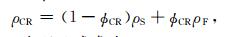
(14)

其中ρS和ρF由(10)式求出.

(Ⅲ)孔隙度与密度-纵波速度平方的线性方程.式(5)可以等价地写成如下线性方程:

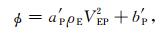
(15a)

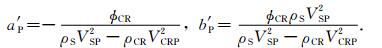
(15b)

根据实验得到的综合介质的纵波速度VEP(φ)和密度ρE(φ)，应用最小二乘法拟合确定直线方程(15a)式及(15b)式a′P和b′P系数.于是临界点和骨架的纵波速度VCRP和VSP分别为

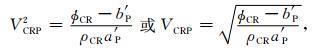
(16)

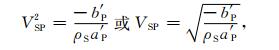
(17)

其中ρCR、ρS和φCR分别由(14)、(10)和(12)式求出.上述孔隙度与密度的线性方程、孔隙度与密度-横波速度平方的线性方程和孔隙度与密度-纵波速度平方的线性方程是数值计算的3个基本方程.

(Ⅳ)其他有关弹性参数的数值计算公式.

这些参数分别为骨架剪切和体积模量、临界点和流体的体积模量、流体的速度.

骨架的剪切模量μS为

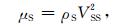
(18)

其中ρS和VSS分别由(10)和(13)式求出.骨架的体积模量KS为

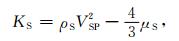
(19)

其中ρS、μS和VSP分别由(10)、(18)和(17)式求出.

临界点的体积模量KCR为

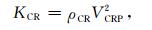
(20)

其中ρCR和VCRP分别从(14)和(16)式求出.

流体的体积模量KF为

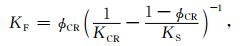
(21)

其中，φCR、KCR和KS分别从(12)、(20)和(19)式求出.

流体的速度VFP由(22)式求出，

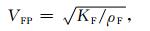
(22)

其中ρF和KF分别由(10)和(21)式求出.

4 数值计算的步骤和注意的问题 4.1 计算的步骤

数值计算步骤按照先后顺序彼此逻辑关联构成一个有机的整体，计算的次序和过程如下:

第1步:基于孔隙度与密度的线性方程，数值计算骨架和流体的密度，参见(9)~(10)式.

第2步:基于孔隙度与密度-横波速度平方的线性方程，数值计算临界点孔隙度和骨架横波速度，参见(11)~(13)式.然后利用(14)式求取临界点的密度.

第3步:基于孔隙度与密度-纵波速度平方的线性方程，数值计算临界点和骨架的纵波速度，参见(15)~(17)式.如果(16)式求出的临界点速度为虚数，则应该对(12)式初始求取的临界点孔隙度进行有效的微调，直到临界点速度为实数.

第4步:数值计算骨架的剪切及体积模量、临界点的体积模量和流体体积模量，进而求取流体的速度，参见(18)~(22)式.

分析判别所求弹性参数数值结果的合理性和可靠性，不满足时则微调第2步中(1 2)式求出的临界点孔隙度，然后重复第2步至第4步，直到获得满意的数值计算结果.

4.2 注意的问题

数值计算过程中需要注意以下几点:

(Ⅰ)临界孔隙度的数值不是严格意义的“一个固定点值”.

从理论讲，临界孔隙度应该是一个确切的“点”即孔隙度存在确定的数值；从实际讲，对于测试或观测的样品数据，其本身存在人为和客观不可避免因素引起的误差.因此基于数值计算误差和精度分析的理论表明，临界孔隙度的数值应该分布在“以真实数值为中心的有限小区间内”，该区间的半径与测试数据的品质有关，品质高的数据对应半径较小的区间，反之区间的半径略大.在该小区间内的数据，只要数值计算的可靠性和精度满足要求，都可以视它们为所求取的临界点孔隙度.

(Ⅱ)临界孔隙度数值的敏感性.

敏感性的含义为，临界孔隙度数值的微小摄动都会对“临界点和流体”的密度及体积模量数值产生较大的波动.这种摄动的后果可能使有关参数数值计算的结果失去应有的物理含义，例如，若临界点处孔隙度及密度数值的不合适，式(16)计算的临界点速度可能是虚数，并且波及到干样品气体的速度也为虚数.反之利用临界孔隙度数值“摄动”的敏感性，可以采用微调搜索方式有效地求取临界孔隙度的合理数值.

(Ⅲ)临界孔隙度的数值可以运用微调搜索方式予以求取.

首先由(12)式求出临界孔隙度的初始数值，由此能够确切指明“意欲求取的临界孔隙度数值”分布在初始数值的附近；然后围绕初始数值进行孔隙度数值的微调搜索，数值微调搜索的幅度应与测试数据的误差尽量一致，也可以视情况灵活地选择.例如，本文的做法是取临界孔隙度初始数值的±1%作为微调搜索的步长.每微调搜索到临界孔隙度的一个数值，都要从第2步骤至第4步骤重复进行数值计算，并对数值计算的流体速度等参数进行合理性判别，直到获得满意的结果.

(Ⅳ)必要的约束条件和先验信息.

①数学上的约束表现为(16)式求取的临界点速度为实数；如果临界点速度为虚数，则应该对(12)式初始求取的临界孔隙度数值进行有效的微调，直到临界点速度为实数.②物理上的约束表现为(22)式求取的流体速度具有合理的意义；例如本文室内干样品含气的速度不可能为虚数，而且数值分布在0.350~0.450 km/s是较为合理并是可以接受的范围；这些判据可以帮助控制“微调搜索”的进展程度. ③更为一般的情况需要结合具体实际，通过介质样品的物理实验或其他可能的方式获得必要的先验信息，对实现物理约束和保证数值计算结果的可靠性具有重要作用，特别是在一定温度压力条件下的混合流体.

5 岩石样品的数值计算实例

基于前面阐述的数值计算公式和步骤，运用美国劳伦斯-利物莫国家实验室(Lawrence Livermore National Laboratory，Livermore，CA 94550)的干样(可视为含气)24个样品的测试数据[5]，开展了数值计算求取临界点和流体及骨架弹性参数.

5.1 密度参数的数值计算

对于干样(可视为含气)的情况，图 1中孔隙度φ与测试密度ρE关系的拟合直线方程是

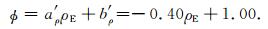
(23)

依据(23)式的结果并运用(10)式的关系，得到骨架密度ρS=2.478949 g/cm3和流体密度ρF=ρW=0.007662 g/cm3.

图 1 孔隙含气时，孔隙度与密度关系的拟合图 Fig. 1 Density versus porosity cross plot by regression fitting for dry samples (viewed as gas-saturated)
5.2 骨架的横波速度和临界孔隙度的数值计算

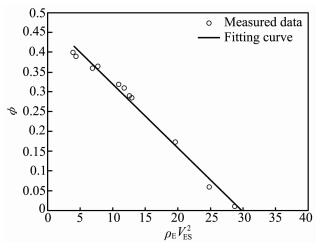
图 2中孔隙度φ与测试数据ρEV2ES关系的拟合直线方程是

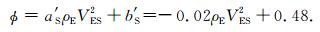
(24)

依据(24)式和(12)及(13)式，得到骨架横波速度VSS=3.498926 km/s和临界孔隙度φCR=0.482268.再由(14)式求出临界点的密度ρCR=1.287127 g/cm3.

图 2 孔隙含气时，孔隙度与ρEVES2关系的拟合图 Fig. 2 The φ-ρEVES2 cross plot and regression line for dry samples (viewed as gas-saturated)
5.3 骨架的纵波速度和临界点纵波速度的数值计算

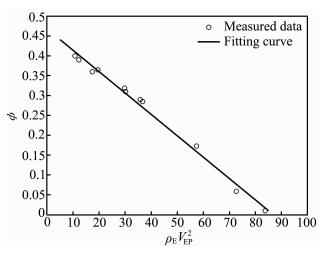
图 3中孔隙度φ与测试数据ρEV2EP关系的拟合直线方程是

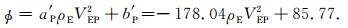
(25)

依据(25)式和(16)及(17)式，得到骨架纵波速度VSP=5.930382 km/s和临界点纵波速度VCRP为虚数.

图 3 孔隙含气时，孔隙度与ρEVES2关系的拟合图 Fig. 3 The φ-ρEVES2 cross plot and regression line for dry samples (viewed as gas-saturated)
5.4 流体速度和相关弹性参数的数值计算

基于(18)至(22)式，骨架的剪切和体积模量分别为μS=30.348487 GPa，KS=46.718559 GPa，临界点的体积模量KCR为负数，流体的体积模量KF为负数和纵波速度VFP为虚数.

显然计算结果VCRP、KCR、KF和VFP不合理，本文将在第6节给出分析、并给出正确的结果.

6 初始计算结果与微调计算结果的比较

初始数值计算的结果汇总在表 1~表 3.分析表 2知道，初始数值计算的流体密度是0.007662 g/cm3，可以确切地认定孔隙流体是气体.而数值计算的气体速度是虚数，这不符合物理意义，为此需要对初始求出的临界孔隙度φCR=0.482268进行微调，然后重复第2步至第4步的数值计算步骤获得新的计算结果.

表 1 含气样品初始计算的临界点参数数据 Table 1 Properties at critical point before fine adjustment
表 2 含气样品初始计算的气体参数数据 Table 2 The initial calculated gas data
表 3 含气样品初始计算的骨架参数数据与测试数据的对比表 Table 3 Comparison between measured data and initial framework data

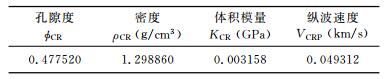
第1次微调后的临界孔隙度为φCR=0.477500，它是对初始求出的临界孔隙度0.482268向下微调约1%的数值.第1次微调并数值计算的结果参见表 4~表 6.从表 5知道，气体速度是0.651478 km/s；表 6中的骨架数值较之表 4的骨架数值基本没有变化.由此表明，临界孔隙度的微小摄动对“刚性”的骨架影响很小，而对“柔性”的气体(弹性参数)会产生敏感的变化；另外从数值计算分析讲，满足计算要求的临界孔隙度的数值分布在“真实数值附近很小的小区间内”，它不是一个“死板的固定数值”.鉴于样品测试是在室内进行的，本次计算的气体速度0.651478 km/s显得略大一些，为此需要进行第2次微调并数值计算.

表 4 含气样品第1次微调并计算的临界点参数数据 Table 4 Properties at the critical point after the first adjustment
表 5 含气样品第1次微调并计算的气体参数数据 Table 5 The calculated gas data after first adjustmen
表 6 含气样品第1次微调并计算的骨架参数数据与测试数据的对比表 Table 6 Comparison between measured data and the framework adjustment

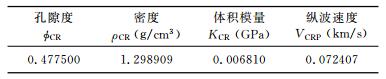
第2次微调后的临界孔隙度为φCR=0.477520，较之第1次的φCR=0.477500略微有所增大.第2次微调并数值计算的结果参见表 7~表 9.表 9中的骨架数值较之表 6基本没有变化，而表 8中的气体速度为0.443679 km/s，较之表 5中的0.651478 km/s有了较大幅度的减少.

表 7 含气样品第2次微调并计算的临界点参数数据 Table 7 Properties at the critical point after the second adjustment
表 8 含气样品第2次微调并计算的气体参数数据 Table 8 The calculated gas data after second adjustment
表 9 含气样品第2次微调并计算的骨架参数数据与测试数据的对比表 Table 9 Comparison between measured data and the second framework adjustment

需要说明的是，文献[5]未给出孔隙内气体的测试数值，因此无法在这里进行计算数据与测试数据的比较；另外气体是模量和密度数值都很小的“柔性”介质，实验中各种条件和影响因素的控制极为复杂.为此我们估算室内测试条件下，孔隙内气体的速度分布在0.350~0.450 km/s是较为合理并是可以接受的数值范围，于是表 8的气体速度0.443679 km/s可以被视为“意欲求取的结果”.当然在此基础上做第3次微调并数值计算，可能会得到小于0.443679 km/s的数值，但是这样也无法进行计算数据与测试数据的比较，因此这步计算在此就不进行了.

7 结论和认识

本文提出了数值计算含气样品临界点以及流体和骨架弹性参数的公式，结合美国劳伦斯-利物莫国家实验室含气砂岩样品的测试数据，按照数值计算的4个步骤，获得了满意的结果，表明了数值计算公式的正确性和实现方法的有效性.主要结论和认识为:

(1)基于实验测试样品的整体密度、横波速度和纵波速度，可以运用数值计算公式(9)至(22)分别求取临界点密度、体积模量和速度3个弹性参数，流体密度和体积模量以及纵波速度3个弹性参数，骨架密度、体积和剪切模量以及纵横波速度5个弹性参数，共计11个弹性参数.

(2)研究成果表明，通过实验方法或其他测试方法，只要给出小于临界点孔隙度的相关弹性数据，而不需要临界点的有关数据，例如劳伦斯-利物莫国家实验室这样的数据，就可以运用本文提出的公式和方法，数值计算临界点以及流体和骨架的弹性参数.

(3)密度是数值计算中的关键参数.密度组分方程严格遵循质量守恒，因此只要数值计算使用的原始密度数据品质好，数值计算的临界点和流体及骨架密度数据是比较可靠的，测试数据与计算数据的相关系数均可达到95%以上.数值计算的流体密度数据可以明确地指示孔隙内流体的物质属性，例如本文的流体为气体，进而为后续临界点和气体速度等参数的计算提供了关键的指示作用.

(4)临界孔隙度是另一个关键参数.基于测试数据本身存在人为和客观等不可避免因素引起的误差，同时为保证后续数值计算能够正确并合理地进行，因此允许对初始求出的临界孔隙度及密度进行数值上的必要微调.对于本文含气样品数据，共进行了2次微调并数值计算，结果是可信并可接受的.

(5)数学和物理的约束是保证数值计算过程顺利和求取结果可靠的基础.数学约束表现在有关公式中开根式求取速度时不能出现虚数的情形；物理约束体现在所求参数的数值具有合理的物理含义；通过对初始求出的“临界孔隙度数值”的合理微调，可以落实数学和物理的约束.另外通过其他可能的方式尽量获得必要的先验信息，例如一定温度压力条件下的混合流体，这对保证数值计算结果的可靠性具有重要作用.

本文提出的数值计算公式及方法物理意义清晰，表达形式直观简洁，为孔隙流体介质的数值计算分析和流体属性研究提供了新方法和新途径.通过理论与实践研究的不断深化，可以进一步地完善和发展这种数值计算方法.

致谢

感谢美国劳伦斯-利物莫国家实验室的样品数据，感谢本文所用参考文献的各位学者专家.尤其感谢匿名的审稿专家以及编辑们提出宝贵意见.

参考文献
[1] Nur A, Mavko G, Dvorkin J, et al. Critical porosity, the key to relating physical properties to porosity in rocks. In:Proc, 65th Ann Int Meeting, Soc Expl. Geophys , 1995: 878.
[2] Nur A, Mavko G, Dvorkin J, Doron Galmudi (Stanford Rock Physics Laboratory). Critical porosity:A key to relating physical properties to porosity in rocks. The Leading Edge , 1998, 17: 357-362. DOI:10.1190/1.1437977
[3] Mavko G, Mukerji T, Dvorkin J. The Rock Physics Handbook. New York:Cambridge University Press , 1998: 221-224.
[4] Chen Q, Nur A. Critical concentration models for porous materials. In:Yavuz Corapcioglu M ed. Advance in Porous Media. New York: Elsevier, 1994 : 169 -308.
[5] Patricia A Berge, Brian P Bonner, James G Berryman. Ultrasonic velocity-porosity relationships for sandstone analogs made from fused glass beads. Geophysics , 1995, 60(1): 108-119. DOI:10.1190/1.1443738
[6] 聂建新, 杨顶辉, 巴晶. 含泥质低孔渗各向异性黏弹性介质中的波频散和衰减研究. 地球物理学报 , 2010, 53(2): 385–392. Nie J X, Yang D H, Ba J. Velocity dispersion and attenuation of waves in low-porosity-permeability anisotropic viscoelastic media with clay. Geophys (in Chinese) , 2010, 53(2): 385-392. DOI:10.3969/j.issn.0001-5733.2010.02.016
[7] 石玉梅, 姚逢昌, 孙虎生, 等. 地震密度反演及地层孔隙度估计. 地球物理学报 , 2010, 53(1): 197–204. Shi Y M, Yao F C, Sun H S, et al. Density inversion and porosity. Geophys (in Chinese) , 2010, 53(1): 197-204. DOI:10.3969/j.issn.0001-5733.2010.01.022