2. 迈阿密大学地质与地球物理系,美国佛罗里达州迈阿密 33149
2. Division of Marine Geology and Geophysics, University of Miami, Miami FL 33149, USA
地震定位是地震学的基本问题之一.地震学中的很多研究都依赖于地震定位的结果,如研究地震活动性图像、地震与活动构造的关系等,为此,地震学家们一直不断改进或提出新的定位方法,致力于减小定位误差、提高定位的精度.
常规的地震定位就是利用P波和S波到时的观测资料,结合参考的速度结构模型,来反演出震源最合适的空间位置和发震时刻,有时还给出对定位结果的评价,如给出定位精度等.由此可见,震相到时读取的可靠性、所使用的速度结构模型是否合适、台站分布是否合理以及所采用的地震定位方法等因素都会影响地震定位精度.在假设台站布局合理的前提下,地震参数测定精度主要的误差源不外乎两个方面,一是震相到时读数存在误差;二是计算走时的速度结构模型所引起的误差[1].为了减小震相到时读数误差,可以通过赋予不同震相不同的权值来减小影响;近年来波形互相关技术的发展更是提高读数精度有效方法,可以使某些震相到时读数精度高达几毫秒[2].而用简单的速度结构模型代替复杂的地壳结构将会对地震参数的确定产生系统误差,且这比震相到时读取精度所引起的误差显著得多[3],所以在地震定位中使用横向均匀的一维速度模型是造成定位精度不高的重要原因.
为了减小速度结构模型简化所引起的定位误差、提高绝对位置精度需要得到更加精细的速度结构,通常采用震源参数与速度结构的联合反演来解决.然而,近些年来相对定位方法发展迅速,旨在弥补速度模型简化所引起的误差而并非解决速度结构模型本身,其利用多个地震事件联合定出多个震源参数,提高相对位置精度,且大量事件的同时定位也使定位效率得以提高;主事件方法、双差定位方法(Double-Difference Algorithm,DD)以及本文所介绍的特定震源台站校正定位方法等都是相对定位方法.
其中双差定位方法有其独到的优点而被广泛使用,国内外已有很多学者应用该方法对不同地区的地震重新定位研究,取得了较好的效果[4~9];但双差方法只对地震群中的事件进行重新定位,对孤立的事件不做定位,因此要对输入的事件都进行定位,就必须组织成地震群[10];很多地震由于不满足双差定位的条件而受到限制不能参与定位,这使得重新定位后的地震数目大为减少,不利于地震学中一些基本问题的研究;或是为了让更多地震参与重新定位而必须降低限制条件,但这样又会使定位效果不佳,这使人们常常感到双差定位的条件较为苛刻,尤其在我国台站分布较为稀疏的区域;为了弥补这一缺陷,得到更多地震重新定位的结果,有研究者采用将双差方法与其他方法结合互补优缺来达到目的,如黄耘等就将双差方法与遗传算法结合进行重新定位研究,取得了一定的效果[8].
本文将引进并使用另一种相对定位方法---特定震源台站校正法(SSST)[3].有研究表明,该方法与主事件方法及双差定位法的定位能力相当[11];且重新定位后地震缺失较少.该方法最近被用来定位美国南加州从1981到2005年的所有地方震,取得很好的效果[12].本文中采用了特定震源台站校正与双差这两种方法对研究区域地震进行重新定位研究,并对结果进行了初步比较分析.
安徽霍山地区地质构造复杂,历史上1917年1月24日发生了一次Ms6.3级强震,该区域现今小震仍十分活跃,是安徽省地震局重点监测的地区;有研究者对该区域的地壳速度结构进行了研究,这些都为地震定位方法的测试提供了较好条件.
2 特定震源台站校正定位方法 2.1 目标函数的构建与求解从数学角度来说,各种地震定位方法的实质都是求解目标函数的极小值,区别在于目标函数的构建、处理及求解的方法不同[13],所以目标函数的构建与求解是任何定位方法都必须解决的问题.
常规的地震定位方法都采用最小二乘法则(L2准则)来构建目标函数,但使用L2准则受异常值影响较大,而且使用前提是走时残差遵循正态分布,但这点常常得不到满足[14].此时可以采用L1准则,即最小化残差的绝对值之和;有研究表明,使用L1准则可降低异常走时残差的影响且使得结果更加稳健[15, 16].特定震源台站校正方法源程序提供了几种准则可以选择,便于讨论,本文以L1准则为例.
由于走时是空间坐标的非线性函数,因此地震定位是个非线性最优化问题.特定震源台站校正定位方法求解采用的则是完全非线性的格点搜索法,优点在于不用求偏导数,迭代过程稳定.该方法大致如下:以每个地震事件为中心构建三维立体网格,这样得到立体各顶点、各边中点、各面中心点及包括地震事件位置在内的27个位置格点,将残差最小值所对应的点位置作为该地震的震源位置,此次迭代结束;下一次迭代时候以所得位置为中心,同时缩小网格宽度重新构建立体网格进行搜索,从而得到地震新的震源位置;经反复迭代直至结果稳定而得到最合适位置.
2.2静态台站校正定位方法(Static Station Term)
在介绍特定震源台站校正定位方法之前,首先需要说明静态台站校正方法.设有M个地震,N个台站.对地震i和观测台站j(i=1,2,…,M;j=1,2,…,N),走时残差为
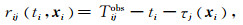
|
(1) |
其中rij(ti,xi)是第i个地震到第j个台站的走时残差;ti和xi是第i个地震的起始时刻与位置;Tijobs是第i个地震到达第j个台站的观测到时;τj(xi)是第i个地震到第j个台站的计算走时.
为了减小速度结构模型简化所引起的误差,在此引入台站校正项,将介质非均匀结构对走时的影响归结为台站校正值,即将台站校正项加到计算走时上.若不同地震在同一台站的台站校正值是相同的,则称为静态台站校正方法.此时采用L1准则构造的目标函数为
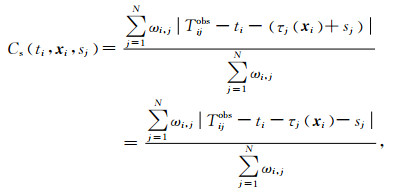
|
(2) |
式中ωi, j是第i个地震在第j个台站数据提取权重;sj为地震在第j个台站校正值.
经过两步过程实现目标函数的极小化:第一步迭代:固定台站校正项不变,此时目标函数只是震源参数的函数.在这步中,简单地把台站校正项和观测到时项放在一起而得到校正的观测到时,即Tij'obs=Tijobs-sj,用这个校正的观测到时Tij'obs代替真实的观测到时进行定位;第二步迭代:固定震源参数不变,目标函数只是台站校正项的函数.在这步中,如(2)式所示,每一个台站校正值通过所有地震到该台的残差计算得到.重复上述两步骤几次,直至得到稳定的台站校正值与震源参数,就可得到定位结果.
2.3 特定震源台站校正定位方法(SSST)当地震群体的空间范围很小时,静态台站校正方法大大提高了地震的相对位置精度;而当地震活动范围广且射线路径存在高度异常体的时候,所有地震在同一台站校正值相同显然是不合理的,这就在很大程度上限制了地震群体的空间范围,这一弊端和主事件法类似.为解决这个问题,不同地震在各个台站的校正值不再单一,而是随着震源空间位置的变化而变化,即每个台站的走时校正项是震源位置的函数.应用于地震定位研究,参数化台站校正由Pavlis和Hokanson于1985年提出[17];最初实现此想法是将研究区域分成几个小的区域,同一台站对不同小区域地震的校正值是不同的,而在每个小区域内的所有地震对同一台站则具有相同的校正值;但这样做有缺陷,如地震分布密度不均、小区域的边界处台站校正值的不连续等[3].
Richards-Dinger和Shearer在2000年提出特定震源台站校正地震定位方法[3],该方法很好应用了每个台站的走时校正项是震源位置的函数这一想法,为每个震源-台站对单独计算校正值,具体如下:以地震事件i为中心,将其周边的N个地震到台站j的残差,经过计算的结果作为该地震到这个台站的校正值si,j,这样每个地震在各个观测台站都有着不同的台站校正值,即台站校正项是随震源空间位置变化的函数.值得注意的是,如果N等于总的地震数,所得结果将和静态校正一样;如果N等于1,会由于每个地震计算的台站校正值完全独立而失去意义.所以N要根据不同的情况加以选择.由于地震分布疏密程度不同,如何在每个地震事件周边选择N个最合适的相邻地震是关键,Richards-Dinger和Shearer选择了计算几何学中常用的Delaunay算法.
2.4 特定震源台站校正定位方法的改进最初Richards-Dinger和Shearer应用特定震源台站校正法对南加州地震进行精确定位研究的时候,他们首先使用静态台站校正方法得到地震的初始位置及台站校正值,然后在此基础上进行特定震源台站校正的计算重新定位,这样在得到地震的相对位置之前绝对位置精度也有一定程度的提高[11, 18].
林国庆于2005年对上述方法加以改进,即选择每个地震事件周围指定半径球面内所有地震的残差为该地震计算在各个台站的校正值,且在迭代过程中不断缩小选震半径,也就是说,开始使半径足够大以至包括所有地震,而在每一次迭代过程中逐渐缩小直至到指定的某个最小值.林国庆使用该方法及双差等几种定位方法进行测试,结果表明,该方法与主事件法及双差法定位能力相当,且数据量大时运行速度较双差法快[11, 18].本文使用的就是此处改进特定震源台站校正方法源程序.
值得注意的是:特定震源台站校正法的地震定位部分和台站校正部分是分开计算的,定位部分不仅可以使用格点搜索方法,当然也可以结合使用任何其他的单一事件定位方法.
应用特定震源台站校正法对地震重新定位的整个过程大致可以分为以下几个步骤:
(1)对速度结构模型进行线性插值,并计算走时表文件,用于格点搜索定位计算;
(2)利用格点搜索法对单个地震事件定位,为后面相对定位提供震源的初始位置;
(3)用静态台站校正方法进行几次迭代直至得到稳定的地震位置与台站校正值;
(4)再进行特定震源台站校正项的计算,经多次迭代直至收敛得到最合适的地震位置作为定位结果.
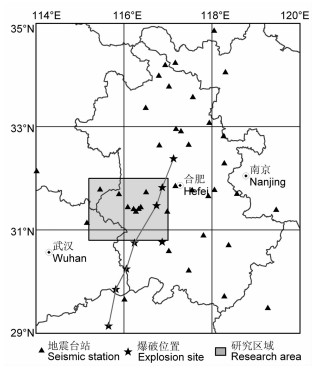
3 地震重新定位过程与结果 3.1 研究区域及资料的选取选择鄂豫皖交界处大别山东北端的霍山地区为研究区域,范围为30.8°N~32.0°N,115.2°E~117.0°E.收集了安徽省1976~2008年的地震台网观测报告,1976年前仪器记录到的资料缺失而显得相对不完整,尤其是发生于1973年的霍山震群震相资料缺失,1982年马秀芳在国内最早使用相对定位方法,就是对此次震群进行重新定位研究[19].部分震级偏大的地震也使用了邻省记录到的数据并进行了合并.我们对这些资料进行整理,对资料不清楚震相、差错数据进行剔除.最后选出ML≥1.0的地震共有2024次,震级在ML1.0~4.3之间,共有18451条震相数据,其中P波震相有8891条,S波震相有9560条.研究区域位置与震相报告中所使用的观测台站分布见图 1所示(注:部分台站现已不再使用或是在原位置上数字化改造).
|
图 1 研究区域位置及台站分布 Fig. 1 Overview of research area and distribution of seismic network |
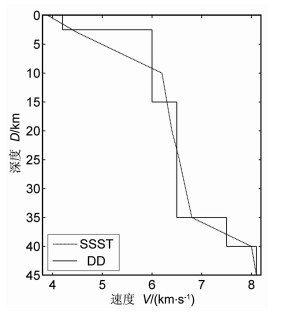
该区域的人工地震研究比较丰富,王椿镛等人在大别山区域进行了8次人工爆破(如图 1),沿测线给出了相对精细的速度结构图[20, 21];董树文等人也使用此爆破资料进行研究,认为大别山腹地至今仍保留6~8km厚的山根[22].本研究在充分吸收前人的基础上给出研究区域的一维地壳速度结构初始模型(图 2),波速比取值为1.72.
|
图 2 特定震源台站校正及双差法P波速度模型 Fig. 2 P wave velocity model for the SSST and DD methods |
双差方法使用的是层状一维速度结构模型,而特定震源台站校正方法采用的则是经过线性插值后相对光滑的速度结构.
3.3 特定震源台站校正法定位过程及结果从测震学角度看,一般P波到时读取质量要好于S波.因此,我们对源程序进行修改,加上可以赋值权重的部分,对P波和S波分别赋予1.0和0.5的权重.经特定震源台站校正法重新定位后,有1982次地震参与了重新定位,约占总数的98%;为了保证解的稳定性,设定震相观测数小于5的地震不参与重新定位,没有参与重新定位的42次地震中,有很多是由于不符合此条件而缺失.经过重新定位,地震震中分布也由定位之前的“网格状”分布变得十分紧凑,丛集性更加明显、效果显著(见图 3).
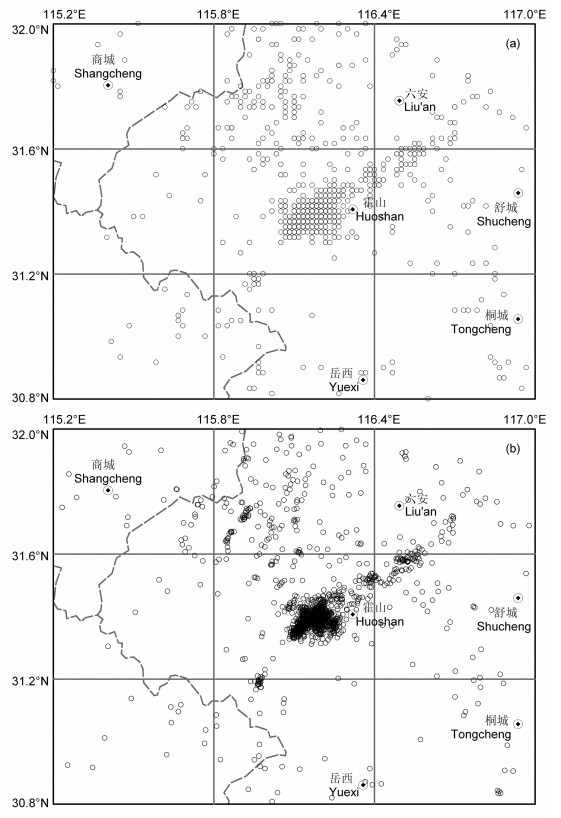
|
图 3 霍山地区1976~2008年地震经特定震源台站校正法重新定位前(a)、后(b)震中分布 Fig. 3 Map view of epicenter distribution before (a) and after (b) the SSST relocation between 1976 and 2008 in the Huoshan area |
应用bootstrap法对定位结果作出评价[23, 24],具体做法如下:对重新定位后每个地震震相的残差进行随机选择,并把选出残差值加在相应的地震各个震相理论走时上(每个数据可能被选择多次或不被选择),然后用这个数据去重新定位,得到所有地震新的位置;重复取样n次,这样就得到每个地震n次新的震源位置.计算n次新位置的标准偏差作为每个地震定位的偏差,取所有地震定位偏差的均值作为定位误差.当数据量大的时候,这样做法的统计不确定性非常小.条件许可时重复取样次数越多则结果更加可靠.本文n取值为30次,得到E-W、N-S、U-D三方向的定位误差分别为0.4km、0.6km、0.9km.
图 4与图 5给出了定位前后震源深度的分布情况.重新定位前,有20%的地震未给出震源深度,重新定位后,99%的地震给出震源深度参数,只有24次地震未给出;震源深度在5~15km间的地震次数约占总数的85%,优势分布非常明显.
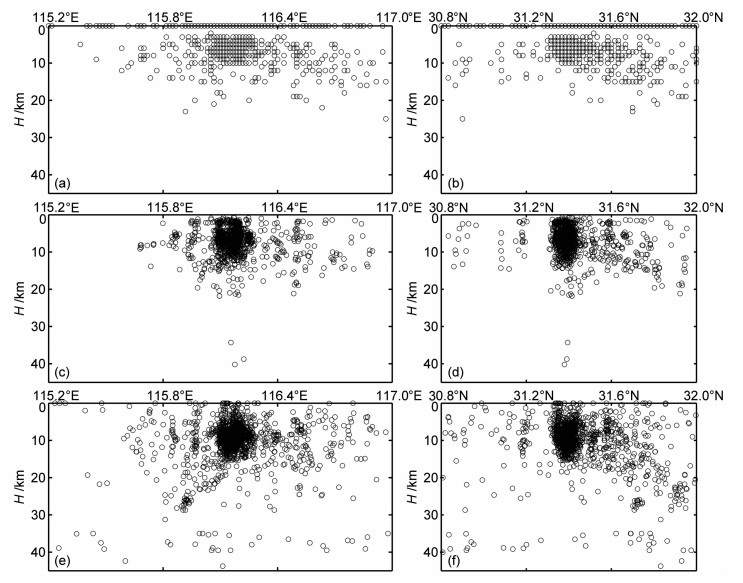
|
图 4 重新定位前后震源深度沿经度(a,c,e)、纬度(b,d,f)方向的分布 (a,b)重新定位前;(c,d)双差法定位后;(e,f)特定震源台站校正法定位后. Fig. 4 Cross-sectional views of seismicity along longitude (a, c, e) and latitude (b, d, f) before and after relocation (a, b) Before relocation; (c, d) After the DD relocation; (e, f) After the SSST relocation |
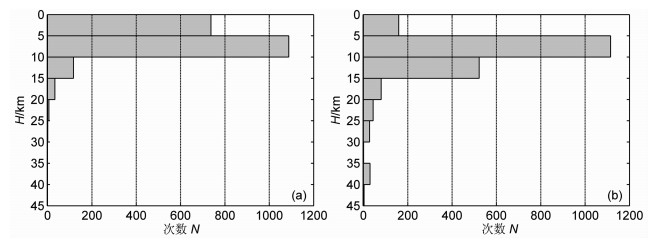
|
图 5 特定震源台站校正法重新定位前(a)、后(b)震源深度分布统计 Fig. 5 Statistics distribution of focal depth before (a) and after (b) the SSST relocation |
为了验证地震初始位置的变动是否对特定震源台站校正法的定位结果产生整体偏移,我们进行了8次测试,即对所有地震的初始位置在经、纬度方向上分别加上、减去5km和10km使其产生整体偏差,经重新定位后发现和最初定位结果一致,震中位置并没有发生整体偏移;究其原因,在于使用台站校正相对定位之前,先使用格点搜索方法对单个事件进行了初步定位,之后在此基础上相对定位,这样不至于产生整体偏差;从这个角度也可以说,特定震源台站校正定位方法也具有部分提高绝对位置的能力.
地震定位问题中,深度是最难测定的,主要原因在于地震发生于几千米甚至几百千米的地下,而地震仪器一般分布于地表或是接近地表的井中,不能有效地包围震源,这使得反演计算中不能很好地约束震源.特定震源台站校正方法使用的格点搜索方法对定位深度的控制一定程度上依赖所使用的速度结构模型,经测试发现模型选择不同可能会造成深度方向上的整体偏移,尤其是浅部速度偏大会使接近地表的浅层地震偏多,这往往也是不太合理的;经过多次测试,本文选择较低的地表初始速度.但震源深度的反演问题仍有待于进一步解决.
3.5 定位前后残差分析重新定位前后地震的均方根残差分布如图 6(图 6b中残差0~0.2s间地震次数为该区间总次数的1/5).定位前地震走时均方根残差分布在5.0s以内,由于震相数据原因,还有早期的几次地震均方根残差值异常大,校正查核比较困难,此处不再特别处理.经过重新定位后,几乎所有地震均方根残差的分布在1.8s以内,其中1.0s以内的占总数的99%,绝大多数地震都分布在0.2s以内,约占总数的90%.还有几次地震残差偏大,究其原因,可能在于震中初始位置误差过大,以至于格点搜索设置为30km的边长仍过小,而不能得到最合适的位置所致.通过比较,重新定位前后均方根残差的均值从1.34s降至0.11s,得以大幅度地减小.
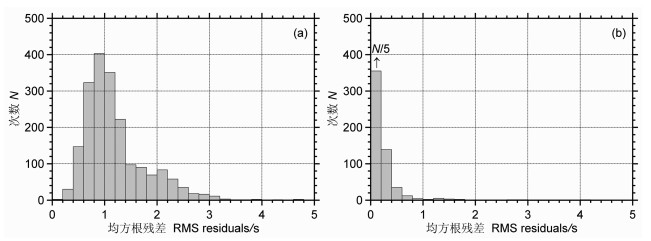
|
图 6 特定震源台站校正法重新定位前(a)、后(b)均方根残差统计图 Fig. 6 Statistics histogram of the RMS residuals for all earthquakes before (a) and after (b) the SSST relocation |
双差方法与特定震源台站校正方法本质上一样,都使用周边地震来校正走时残差、在一定程度上消除地壳速度结构横向不均匀性带来的误差;区别在于双差方法认为相近的地震事件到同一观测台站具有近似相同的路径,通过事件对的残差相减消去了这个路径偏差而得到双重残差;而特定震源台站校正方法则是利用周边地震事件为每个地震计算出了这个偏差.此外,两种方法的速度结构模型有所不同,前面已有所叙述.
值得注意的是,这两种方法只能用于初至波,而不是单一的直达波[9],为了防止Pg/Pn或Sg/Sn混淆,Richards-Dinger等在南加州选择震中距120km范围的地震事件参与计算[3];应用到本文的研究区域,由于观测台站较为稀疏,选取120km的震中距会使参与定位的地震数量减少,故适当放宽至150km.严格来说,若能确保所使用的均为初至P波和S波数据则结果可靠,但由于波形难于识别等原因,很多时候直达波与首波并没有加以区分,这会对结果有些影响,尤其是对震源深度上的影响,所以定位时尽可能多的将初至波包含进来,但多数情况下往往受到所使用数据的限制而只使用直达波.
4.2 两种方法定位结果初步比较为了比较,亦采用双差方法对上述地震重新定位.在双差定位处理中,首先对地震进行组对,选取走时观测记录数大于等于6、震源间距小于10km、距观测台站150km范围内地震走时进行两两相互组合,最后组成地震群参与定位的地震有1644次.同样,P波和S波分别赋予1.0和0.5的权重,经过反复迭代后得到1303次地震高精度的震源位置.比较同一地震定位前后位置,可得到各个地震在E-W、N-S、U-D三方向的偏移,并求出平均值分别为0.9km、1.2km、2.1km.
对比两种定位方法结果可知,双差方法重新定位的地震为1303次,约占地震总次数2024的比例为64%,远低于特定震源台站校正方法.从深度上来看(图 4和5),双差法较特定震源台站校正法定位结果稍微偏浅,如前所述,深度上差异在于地震定位本身对震源深度难以控制,不同方法使用速度模型有所不同以及定位后数量不同等原因造成.但总体来说,两种方法定位后震源深度绝大部分都集中在15km之内,这也说明该区域浅源地震十分发育,与他人研究结果一致[8].同时也可以看出,相对于双差法,特定震源台站校正法定位后在20km以下深度还有一定次数的地震,尤其在30km以下还零散分布一些,不会因为周边地震次数偏少定位后缺失,而是尽可能使用周边地震来校正其震源参数,若是地震对之间距离偏大不利于相对位置校正时,也会由格点搜索后给出具有一定精度的单个地震事件震中位置.
有研究表明,应用近台资料时,双差法有可能给出一定精度的绝对位置[25].为了验证双差法对初始位置的依赖程度,类似上述特定震源台站校正定位方法对初始位置进行的偏移处理,经双差方法重新定位后发现,地震群的整体随着初始位置的偏差而产生了偏移.从这个角度可以说,虽然双差方法相对位置控制得很好,但绝对定位的作用则较小,很大程度上依赖初始位置.
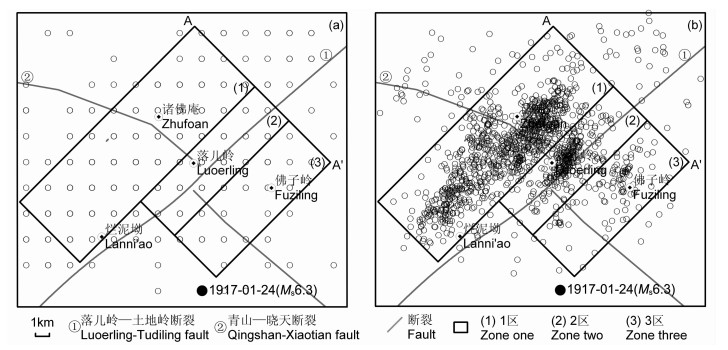
4.3 佛子岭-诸佛庵震群时空分布特征自1970年安徽地震观测台网建立以来,发现位于安徽境内的霍山地区小震持续不断,其中佛子岭-诸佛庵一带小震活动频次和强度尤为突出,主要发生在北东向落儿岭-土地岭与北西向青山-晓天断裂的交汇处[26].重新定位前,该处地震目录所给出的震中位置精度低,平面上绝大部分震中位置重叠而显示出“网格状”,经重新定位后发现该处震群由3条明显的密集条带组成.为了进一步分析该区域小震活动的时空分布特征,我们沿地震分布相对稀疏的区域为边界划分了3个密集区域(图 7),可以看出,这3个小震密集条带呈现北东向分布,整体与落儿岭-土地岭断裂方向大致一致.而在深度上统计表明,这3个密集区地震绝大部分都集中在5~15km之间,优势分布非常明显;其中震源深度在10km以内的地震最为密集,约占总数的72%,具有震源深度较浅的特征.
|
图 7 佛子岭-诸佛庵地区震群特定震源台站校正法定位前(a)、后(b)分布 Fig. 7 Distribution of Fuziling-Zhufoan swarm before (a) and after (b) the SSST relocation |
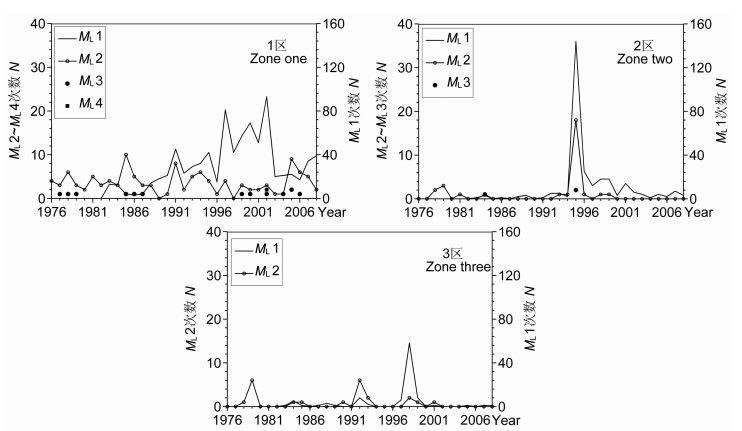
将各个密集区内地震分不同震级计算每年的地震次数,并绘于图 8.图中ML1地震次数绘于右轴,其他震级地震次数绘于左轴.从图 8可以较为清楚地看到,各个密集区地震随时间的分布是不同的(20世纪90年代以前由于台网监测能力不足,ML1地震可能缺失较多),1号密集区地震一直持续不断、随时间的分布总体上看较为均匀;而2号和3号密集区地震随时间分布极不均匀,曲线呈现出脉冲状,且这两个区域地震主要是1995年和1998年的峰值年地震次数剧增形成.
|
图 8 密集区地震年频次曲线图 Fig. 8 Temporal-distribution of the earthquakes in seismic density zones |
通过分析定位误差的主要原因,详细介绍了特定震源台站校正地震定位方法并应用于安徽霍山地区;重新定位后结果表明,地震分布更加紧凑,条带状分布更加明显;应用bootstrap法对定位偏差进行估计,得到水平、垂直向的相对误差都在1km以内;定位残差也得以显著地降低,均方根残差的均值从定位前的1.34s下降到定位后的0.11s.其中位于霍山县的佛子岭-诸佛庵一带小震震群,重新定位前后由一个地震丛集变为3条明显的密集条带;分析结果显示,这3个密集条带区震源深度上分布都较浅,而随时间的分布却有所不同.
通过与双差法初步比较可知,特定震源台站校正定位法并不需要组成地震群、定位条件容易满足,且求解使用的是非线性的格点搜索方法,不会出现解的稳定性问题,这些都有助于使更多的地震参与重新定位;而双差方法由于需要满足组成地震对条件、定位过程中大型矩阵的反演会出现解的稳定性问题,都会使得参与重新定位的地震数目大为减少.经过测试初始位置对两种方法定位结果的影响,发现特定震源台站校正定位方法对初始位置依赖较小、具有一定的绝对定位能力;而双差方法则很大程度上依赖初始位置,否则定位结果可能会产生整体偏差,绝对定位能力较小.以上都说明,特定震源台站校正法是一种较好的地震重新定位方法,易用且结果可靠,能给出相对完整的高精度地震目录,为地震学中的一些研究提供可靠基础数据.
地壳三维速度结构的反演可以减小大尺度异常体的影响而提高震源的绝对位置精度,这可为特定震源台站校正法相对定位提供可靠初始绝对位置;条件许可时,结合波形互相关技术的使用可以进一步提高定位精度,这些都是将来研究的方向.
致谢感谢中国地震局地球物理研究所王椿镛老师提供了大别山爆破点位置数据以及对研究区域的速度模型选择提供帮助;张天中老师、郑秀芬老师对本工作给予很多支持与帮助,在此深表谢意;安徽省地震局为本文提供了震相观测报告及断裂数据,亦表示感谢.
| [1] | 黄媛. 结合波形互相关技术的双差算法在地震定位中的应用探讨. 国际地震动态 , 2008, 4: 29–34. Huang Y. Study on the application and development of the DD algorithm with cross correlation of waveform data in the earthquake location. Recent Developments in World Seismology (in Chinese) , 2008, 4: 29-34. |
| [2] | Schaff D P, Richards P G. Lg-wave cross correlation and double-difference location: application to the 1999 Xiuyan, China, sequence. Bull. Seism. Soc. Am. , 2004, 94(3): 867-879. DOI:10.1785/0120030136 |
| [3] | Richards-Dinger K B, Shearer P M. Earthquake locations in southern California obtained using source-specific station terms. J. Geophys. Res. , 2000, 105(B5): 10939-10960. DOI:10.1029/2000JB900014 |
| [4] | Waldhauser F, Ellsworth W. A double-difference earthquake location algorithm: method and application to the northern Hayward fault, California. Bull. Seism. Soc. Am. , 2000, 90(6): 1353-1368. DOI:10.1785/0120000006 |
| [5] | 杨智娴, 陈运泰, 郑月军, 等. 双差地震定位法在我国中西部地区地震精确定位中的应用. 中国科学(D辑) , 2003, 33(Suppl): 129–134. Yang Z X, Chen Y T, Zheng Y J, et al. Accurate relocation of earthquakes in central-western China using the double difference earthquake location algorithm. Science in China (Series D) (in Chinese) , 2003, 33(Suppl): 129-134. |
| [6] | 朱艾斓, 徐锡伟, 周永胜, 等. 川西地区小震重新定位及其活动构造意义. 地球物理学报 , 2005, 48(3): 629–636. Zhu A L, Xu X W, Zhou Y S, et al. Relocation of small earthquakes in western Sichuan, China and its implications for active tectonics. Chinese J. Geophys. (in Chinese) , 2005, 48(3): 629-636. |
| [7] | Hauksson E, Shearer P. Southern California hypocenter relocation with waveform cross-correlation, Part 1: Results using the double-difference method. Bull. Seism. Soc. Am. , 2005, 95(3): 896-903. DOI:10.1785/0120040167 |
| [8] | 黄耘, 李清河, 张元生, 等. 江苏及邻区地震重新定位和构造特征分析. 地球物理学报 , 2008, 51(1): 175–185. Huang Y, Li Q H, Zhang Y S, et al. Relocation of earthquakes in Jiangsu and neighboring areas, China and analysis of structural features. Chinese J. Geophys. (in Chinese) , 2008, 51(1): 175-185. |
| [9] | 黄媛, 吴建平, 张天中, 等. 汶川8.0级大地震及其余震序列重定位研究. 中国科学(D辑) , 2008, 38(10): 1242–1249. Huang Y, Wu J P, Zhang T Z, et al. Research of relocation for aftershock sequences of Wenchuan strong earthquake. Science in China (Series D) (in Chinese) , 2008, 38(10): 1242-1249. |
| [10] | 郑钰, 杨建思. 双差算法的剖析及参数对定位的影响. 地震地磁观测与研究 , 2008, 29(3): 85–93. Zheng Y, Yang J S. Analysis of double-difference algorithm and the affect of its parameter in location. Seismological and Geomagnetic Observation and Research (in Chinese) , 2008, 29(3): 85-93. |
| [11] | Lin G, Shearer P. Tests of relative earthquake location techniques using synthetic data. J. Geophys. Res. , 2005, 110(B04304). DOI:10.1029/2004JB003380 |
| [12] | Lin G, Shearer P M, Hauksson E. Applying a threedimensional velocity model, waveform cross correlation, and cluster analysis to locate southern California seismicity from 1981 to 2005. J. Geophys. Res. , 2007, 112(B12309). DOI:10.1029/2007JB004986 |
| [13] | 赵金花, 李波, 陆汗鹏, 等. 单一地震事件与多个地震事件的定位方法及应用. 地震地磁观测与研究 , 2007, 28(4): 15–19. Zhao J H, Li B, Lu H P, et al. The earthquake location methods for single seismic event and a number of seismic events and their application. Seismological and Geomagnetic Observation and Research (in Chinese) , 2007, 28(4): 15-19. |
| [14] | 田玥, 陈晓非. 地震定位研究综述. 地球物理学进展 , 2002, 17(1): 147–155. Tian Y, Chen X F. Review of seismic location study. Progress in Geophysics (in Chinese) , 2002, 17(1): 147-155. |
| [15] | 王椿镛, 王溪莉, 颜其中. 昆明地震台网多事件定位问题的初步研究. 地震学报 , 1993, 15(2): 136–145. Wang C Y, Wang X L, Yan Q Z. Preliminary study of multiple events to Kunming seismic network. Acta Seismologica Sinica (in Chinese) , 1993, 15(2): 136-145. |
| [16] | Shearer P M. Improving local earthquake locations using the L1 norm and waveform cross correlation: application to the Whittier Narrows, California, aftershock sequence. J. Geophys. Res. , 1997, 102(B4): 8269-8283. DOI:10.1029/96JB03228 |
| [17] | Pavlis G, Hokanson N. Separated earthquake location. J. Geophys. Res. , 1985, 90: 12777-12789. DOI:10.1029/JB090iB14p12777 |
| [18] | Lin G, Shearer P. The COMPLOC earthquake location package. Seismological Research Letters , 2006, 77(4): 440-444. DOI:10.1785/gssrl.77.4.440 |
| [19] | 马秀芳. 用相对定位法测定1973年安徽霍山震群的震源位置. 地震研究 , 1982, 5(1): 99–113. Ma X F. Locating the epicenters of the 1973 Huoshan swarm, Anhui province, by the relative locating method. Journal of Seismological Research (in Chinese) , 1982, 5(1): 99-113. |
| [20] | 王椿镛, 张先康, 丁志峰, 等. 大别山造山带上部地壳结构的有限差分层析成像. 地球物理学报 , 1997, 40(4): 495–502. Wang C Y, Zhang X K, Ding Z F, et al. Finite-difference tomography of upper crustal structure in Dabieshan orogenic belt. Chinese J. Geophys. (in Chinese) , 1997, 40(4): 495-502. |
| [21] | Wang C Y, Zeng R S. A crustal model of the ultrahigh-pressure Dabie Shan orogenic belt, China, derived from deep seismic refraction profiling. J. Geophys. Res. , 2000, 105(B5): 10857-10869. DOI:10.1029/1999JB900415 |
| [22] | 董树文, 吴宣志, 高锐, 等. 大别造山带地壳速度结构与动力学. 地球物理学报 , 1998, 41(3): 349–361. Dong S W, Wu X Z, Gao R, et al. On the crust velocity levels and dynamics of the Dabieshan orogenic belt. Chinese J. Geophys. (in Chinese) , 1998, 41(3): 349-361. |
| [23] | Efron B, Gong G. A leisurely look at the bootstrap, the jackknife, and cross-validation. Am. Stat. , 1983, 37(1): 36-48. |
| [24] | Efron B, Tibshirani R. Statistical data analysis in the computer age. Science , 1994, 253(5018): 390-395. |
| [25] | 张天中, 武巴特尔, 黄媛, 等. 近台资料对近震相对定位算法的影响. 地球物理学报 , 2007, 50(4): 1123–1130. Zhang T Z, Wu B T E, Huang Y, et al. Effect of the data recorded at nearby stations on earthquake relative location. Chinese J. Geophys. (in Chinese) , 2007, 50(4): 1123-1130. |
| [26] | 姚大全, 张杰, 沈小七. 安徽霍山地区断层活动习性研究的新进展. 地球物理学进展 , 2006, 21(3): 776–782. Yao D Q, Zhang J, Shen X Q. New advance of fault active behavior research in Huoshan area, Anhui province. Progress in Geophysics (in Chinese) , 2006, 21(3): 776-782. |
 2010, Vol. 53
2010, Vol. 53

