2. 现代工程测量国家测绘局重点实验室, 上海 200092;
3. 德国地球科学研究中心, 波茨坦 14473
2. Key Laboratory of Modern Engineering Surveying, State Bureau of Surveying and Mapping, Shanghai 200092, China;
3. Deutsches GeoForschungsZentrum-GFZ, 14473, Potsdam, Germany
自从1997年精密单点定位(Precise Point Positioning,PPP)被Zumberge等[1]提出以来,国内外学者[2~7]进行了一系列研究,其后处理精度可以达到厘米级[2~7].由于精密轨道、钟差产品一般需要13天之后才能得到,因此,实时精密单点定位的实现成了目前精密单点定位研究的主要内容之一.研究[8]得到,超快速(Ultra-PRD,IGU)轨道径向精度与IGS最终轨道精度相当,IGU轨道每6h进行更新,实时GPS轨道可以通过IGS超快速轨道获得,实时钟差估计成了实时PPP研究的重要内容.目前IGS组织的JPL、欧洲的BKG、GFZ、ESA等知名研究机构正在开展实时全球或区域网络监测以及实时精密单点定位服务的相关研究[9, 10].精密钟差通常通过全球或局域GNSS网络进行估计,但估计参数个数会随着测站数目的增加而增加,严重影响了其实时估计.历元间、星间差分[11]可以消除模糊度、接收机钟差参数,大大减少估计参数的个数.本文采用无电离层组合,基于GNSS参考站网络观测进行卫星钟差的实时估计,采用实时估计得到的钟差进行PPP数据解算,在PPP参数估计时,对对流层延迟予以实时估计.对流层延迟参数的实时估计,对于大气研究、实时天气预报[12]具有重要的意义.
2 基于GNSS网络的实时钟差估计 2.1 相对钟差历元间差的估计非差无电离层相位观测组合为
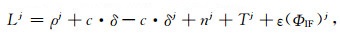
|
(1) |
式中Lj为接收机对GPS卫星j的无电离层相位观测值,ρj为站星距离,c为光速,δ、δj分别为接收机、GPS卫星钟差,nj为组合模糊度,Tj为对流层延迟,ε(ΦIF)j为其他误差项,包括潮汐改正、相位缠绕等以及未被模型化的误差.同一历元,进行星间差分,消去接收机钟差,并整理得到:
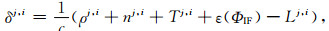
|
(2) |
式中j,i为星间差分算子,表示各相应参数星间差值,如Lj,i为卫星i与卫星j相位观测值之差;δj,i为卫星i与卫星j钟差之差,定义为相对钟差.在没有周跳情况下,进行单站星间、历元间差分,相邻历元n和n-1相减消去模糊度,整理得到:
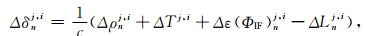
|
(3) |
式中Δ为历元间差分算子,表示各相应参数的历元间差值,如ΔLnj,i为星间差分观测值的历元间差值;Δδnj,i为相对钟差的历元间差.
2.2 基于GNSS网络的相对钟差历元间差的估计基于GNSS参考站网络观测时,由于参考站坐标已知,对流层延迟可以通过Saastamoinen改正模型[13]计算,这样可以通过式(3)进行实时相对钟差历元间差Δδnj,i的估计.设GNSS网络有k个参考站,分别采用每个参考站的观测数据,实时估计相对钟差的历元间差.设由每个参考站估计得到的第n和n-1历元相对钟差之差为Δδn,mj,i(m=1,2…,k),则最终估计值为
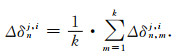
|
(4) |
通过GNSS网络,估计得到相对钟差的历元间差之后,选择一参考历元,设参考历元的相对钟差为δrefj,i,则任意历元的相对钟差为
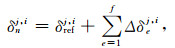
|
(5) |
式中δnj,i为第n历元的相对钟差;Δδej,i为第e和e-1历元间相对钟差的差值;f为参考历元相对于历元n的历元个数.
2.3 相对钟差近似解的估计伪距无电离层观测组合为
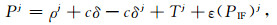
|
(6) |
式中Pj为GPS卫星j的无电离层伪距观测值;ε(PIF)j为其他误差项,包括潮汐改正、相位缠绕等以及未被模型化的误差.同一历元,进行星间差分,消去接收机钟差,并整理得到:
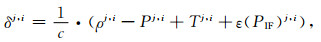
|
(7) |
式中j,i为星间差分算子,表示各相应参数星间差值.由于GNSS网络参考站坐标已知,对流层延迟可以采用模型进行改正,故通过式(7)可进行相对钟差近似解的估计.
3 单站星间差分精密单点定位模型实时精密钟差为基于参考星的相对钟差,根据这一特点,PPP模型推导如下.线性化星间差分公式,设位置参数为XT=|ΔX,ΔY,ΔZ|,可以写为
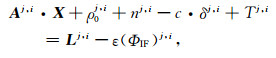
|
(8) |
式中Aj,i为卫星i与卫星j对应的设计矩阵之差;ρ0j,i为站星距离星间差的近似值;对流层参数的估计一般可以表示成一个映射函数和天顶方向延迟的乘积,设Tj,i=m(z)j,iZTD,式中m(z)j,i为卫星i与卫星j对流层映射函数值之差;ZTD为该时刻天顶方向延迟;并设L ′=Lj,i-ε(ΦIF)j,i,把式(5)代入式(8),得到
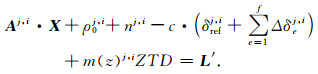
|
(9) |
参考历元的相对钟差δrefj,i在解算过程中会被模糊度参数吸收,设其为Nj,i=nj,i-c·δrefj,i,并定义为伪模糊度;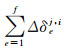
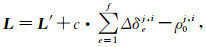
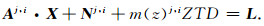
|
(10) |
通过观测方程式(10),就可以进行各参数的实时估计.待估参数为接收机坐标、天顶延迟、伪模糊度.
4 坐标参数初值的求解通过线性化伪距无电离层组合星间差分公式,得到
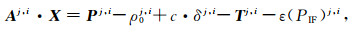
|
(11) |
Δδj,i的近似值Δδ0j,i通过GNSS观测网络实时估计得到,对流层延迟可以通过Saastamoinen改正模型[13]计算.设lj,i=Pj,i-ρ0j,i+c·δj,i-Tj,i-ε(PIF)j,i,则式(11)写为
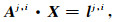
|
(12) |
由(12)式知,估计参数只有坐标参数.当观测卫星个数大于4颗时,就可以进行坐标参数的计算.
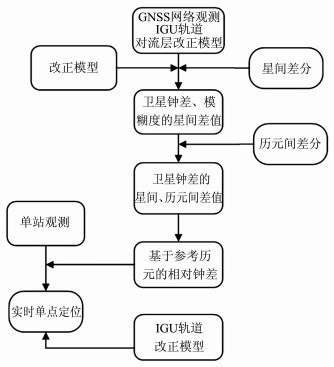
5 实时精密单点定位的实现与精度分析实时PPP的实现,必须以基于全球或局部GNSS网络的实时钟差估计和IGU轨道的下载为前提.目前许多国家和地区建立了全球或局域性的实时参考站网络,如基于IGS-RTPP[10](IGS Real Time Pilot Project),IGS在全球建立了近100个实时站,这些站大部分都是IGS的参考站;还有德国的SAPOS网络[14, 15],日本的GRAPES网络[16]等,我国近年也启动了陆态网络工程,将在全国范围内建立约260个左右实时连续参考站,这为基于GNSS网络进行实时钟差的估计提供了硬件条件.基于以上理论我们进行了实时PPP软件Net-PPP的编写.对应流程见图 1.
|
图 1 实时PPP流程图 Fig. 1 Flow chart of real-time PPP |
本文采用上海GNSS网络9个参考站2009年3月1号24 h、采样间隔为30 s的实时观测数据,进行了钟差的实时估计、发送,采用同济大学GPS基准站24 h、采样间隔为30 s的实时观测数据进行了实时PPP解算.
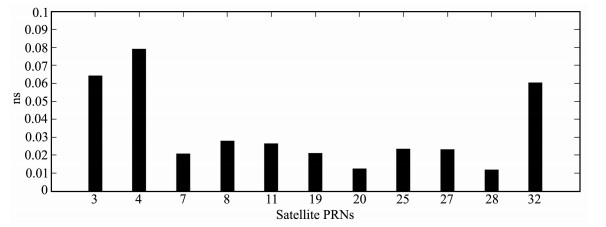
5.1 相对钟差估计结果分析根据本文钟差估计理论、方法,基于GNSS网络可以进行相对钟差历元间差值的估计.选择17号卫星为参考星,来估计其他卫星相对于17号卫星的相对钟差.估计得到的相对钟差的历元间差值与IGS的最终精密钟差相比较,其RMS值如图 2所示.
|
图 2 相对钟差历元间值与IGS最终星历相比较的RMS值 Fig. 2 RMS of the epoch-differenced values of relative clocks compared with the IGS final products |
由图 2可知,基于GNSS网络估计得到的实时相对钟差的历元间差值与IGS的最终钟差相比较,其精度可以达到0.08ns.在估计得到相对钟差历元间差值以及相对钟差近似解之后,进行坐标初值、定位的解算.
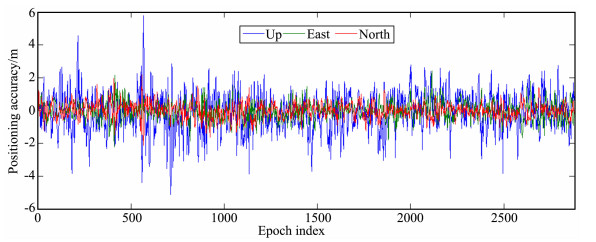
5.2 坐标初值求解及精度分析初值是以伪距观测组合为基础,并结合实时接收到的钟差的近似解来估计坐标参数的值.由于伪距观测值精度较低,所以以其观测组合求解的坐标参数的精度相对较低,但其可作为相位观测解算的初值.实时PPP解算过程中伪距观测组合模型的估计结果划归为以同济大学基准站为中心的站心坐标系(NEU),其结果见图 3.从图 3可以看到,伪距估计值结果在N、E两个方向优于2 m,U方向绝大部分优于2 m,这完全满足相位解算的初值.
|
图 3 伪距估计结果 Fig. 3 The results of code observations |
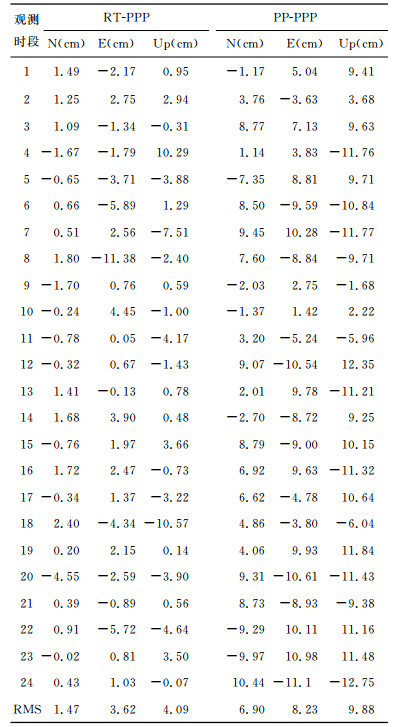
实时PPP解算时,以伪距组合的估计值作为解算初值,然后基于卡尔曼滤波,以相位观测组合进行参数估计,截止卫星高度角10°.为了研究实时PPP静态定位精度以及稳定性,静态解算时,把24 h观测值均分为24个观测值,即就是24个时段,来估计每小时的定位解.同时,在得到IGS最终钟差之后也进行了PPP的后处理.各时段定位结果划归为以同济大学基准站为中心的站心坐标系(NEU)如表 1.
|
|
表 1 实时PPP、后处理PPP每小时解的偏差 Table 1 Difference of hourly static PPP coordinates with respect to the known coordinates in the North, East and Up directions in real-time PPP (RT-PPP) and post-processing PPP (PP-PPP) |
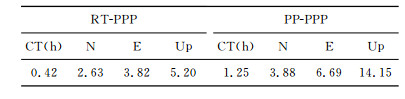
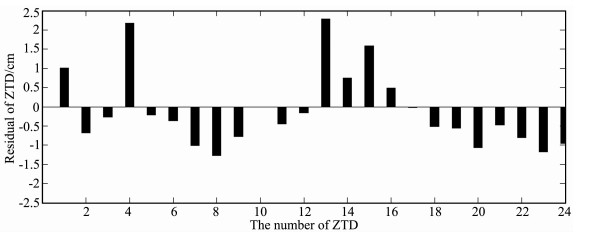
从表 1可以看出,N方向每小时的实时估计结果绝大部分测段的精度优于2 cm,占总测段的92%,100%测段的定位精度可以得到厘米级;E方向绝大部分测段精度优于3 cm,占总测段的71%,96%的测段可以达到厘米级;U方向绝大部分测段的精度优于4 cm,占总测段的79%,92%的测段可以达到厘米级.24个测段解算结果对应的RMS在N、E、U三个方向分别为:1.47,3.62,4.09 cm.以最终轨道与钟差来计算的结果中,N方向优于2 cm的测段只占12.5%,E方向优于3 cm的测段只占8.33%,U方向优于4cm的测段只占12.5%.24个测段解算结果对应的RMS在N、E、U三个方向分别为:6.90,8.23,9.88cm.比较这两种结果可以得到,以本文所采用的钟差估计结果进行实时PPP解算,其结果优于以最终轨道和钟差的计算结果.实时PPP在定位解算的同时,进行了对流层天顶延迟的估计,所估计的对流层天顶延迟与GAMIT软件所估计的结果相比较,如图 4所示.从图 4可得,实时PPP估计结果与GAMIT软件的结果相比较,对流层天顶延迟对应的最大偏差为2.2 cm,相应的RMS值为0.987 cm.在实时精密单点定位解算过程中,对24 h的观测值也进行了动态模式解算,动态模式解算时也分别以估计得到的钟差和IGS最终精密轨道和钟差两种方法进行了解算,对应结果见表 2.从表 2可得,实时PPP的动态解算结果优于以IGS事后精密轨道和钟差进行解算得到的结果,且参数收敛时间速度较快.
|
图 4 ZTD估计结果与GAMIT软件估计结果偏差 Fig. 4 The difference of ZTD between the RT-PPP and GAMIT |
|
|
表 2 参数收敛时间、两种解算结果对应的RMS值 Table 2 Convergence time (CT) and RMS (in cm) of kinematic daily PPP coordinates with respect to the known coordinates in the North, East and Up directions in RT-PPP and PP-PPP |
本文系统性地推导了基于GNSS网络的实时钟差、实时PPP以及初值的估计模型,讨论了模糊度和相对钟差参考历元的和以伪模糊度进行处理的方式,并基于上海GNSS网络9个参考站的观测数据进行了实时钟差估计,采用同济大学GPS基准站的观测数据进行了实时PPP解算.从24个观测时间为1 h的观测时段的定位结果可得,每小时实时PPP的静态定位精度,在N、E、U三个方向可以达到1.47、3.62、4.09 cm.动态定位时,其精度在N、E、U三个方向可以达到2.63、3.82、5.20 cm.与采用最终精密轨道、钟差的解算结果相比较,实时PPP的定位精度优于其定位精度.基于GNSS网络的实时PPP的实现,对于完善、扩大GNSS网络系统的应用范围,进行天气实时预报、气象研究、GNSS移动基准站的实现,以及我国卫星导航服务中心的建设、地壳实时监测都具有重要的意义.但是基于GNSS网络的实时PPP仍然和采用IGS最终轨道、钟差解算时一样,对应模糊度不为整数,因此对于其模糊度的快速固定需要进一步研究.
| [1] | Zumberge J F, Heflin M B, Jefferson D C, et al. Precise Point Positioning for the efficient and robust analysis of GPS data from large networks. Journal of Geophysical Research , 1997, 102: 5005-5017. DOI:10.1029/96JB03860 |
| [2] | Ge G, Gend G, Dick G, et al. Improving carrier-phase ambiguity resolution in global GPS network solutions. Journal of Geodesy , 2005, 79: 103-110. DOI:10.1007/s00190-005-0447-0 |
| [3] | Kouba J, Heroux P. Precise point positioning using IGS orbit and clock products. GPS Solutions , 2001, 5(2): 12-28. DOI:10.1007/PL00012883 |
| [4] | Satirapod C, Homniam P. GPS precise point positioning software for ground control point establishment in remote sensing. Journal of Surveying Engineering , 2006, 132(1): 11-14. DOI:10.1061/(ASCE)0733-9453(2006)132:1(11) |
| [5] | Hu C W, Chen Wu, Gao Shan, et al. Data processing for GPS precise point positioning. Transactions of Nanjing University of Aeronautics & Astronautics , 2005, 22(2): 124-13. |
| [6] | Gao Y, Chen K. Performance analysis of precise point positioning using rea-time orbit and clock products. Journal of Global Positioning Systems , 2005, 3(1-2): 95-100. |
| [7] | Ge M, Gendt G, Rothacher M, et al. Resolution of GPS carrier-phase ambiguities in Precise Point Positioning (PPP) with daily observations. Journal of Geodesy , 2007, 82(7): 389-399. DOI:10.1007/s00190-007-0187-4 |
| [8] | Andre' Hauschild, Oliver Montenbruck. Kalman-filter-based GPS clock estimation for near real-time positioning. GPS Solutions , 2009, 13: 173-182. DOI:10.1007/s10291-008-0110-3 |
| [9] | Muellerschoen R, Bertiger M, et al. An internet-based global differential GPS system, initial results. Proceedings of ION National Technical Meeting, Anaheim, California, January, 2000 |
| [10] | Caissy M. The IGS real-time pilot project-Perspective on data and product ceneration. Report at Streaming GNSS Data via Internet Symposium, 6-7 Feb, 2006, Frankfurt, 2006 |
| [11] | Han S C, Kwon H J, Jekeli C. Accurate absolute GPS positioning through satellite clock error estimation. Journal of Geodesy , 2001, 75: 33-43. DOI:10.1007/s001900000151 |
| [12] | Huang Ching Yuang, Kuo Yinghwa, Chen Shuya, et al. Impact of GPS radio occultation data assimilation on regional weather predictions. GPS Solutions , 2010, 14: 35-49. DOI:10.1007/s10291-009-0144-1 |
| [13] | Jensen A, Ovstedal O. The effect of different tropospheric models on precise point positioning in kinematic model. Survey Review , 2008, 40: 308-173-187. |
| [14] | Weber G. The SAPOS system in Germany oral presentation at the 3rd Asia Pacific Rim Meeting, 6-9 Feb 2001, Tokyo, Japan |
| [15] | Gendt G, Reigber C, Dick G. Near real-time water vapor estimation in a German GPS network-first results from the ground program of the HGF GASP project. Physics and Chemistry of the Earth, Part A: Solid Earth and Geodesy , 2001, 26(6-8): 413-416. DOI:10.1016/S1464-1895(01)00075-8 |
| [16] | Miyazaki S H, Tsuji Y, Hatanka Y. Establishment of the nationwide GPS array (GRAPES) and its initial results on the crustal deformation of Japan. Bull. Geog. Surv. Inst. Jpn , 1996, 42: 27-41. |
 2010, Vol. 53
2010, Vol. 53