2. 吉林大学地球科学学院,长春 130026
2. College of Earth Sciences, Jilin University, Changchun 130026, China
现今,随着地震勘探的深入,一些沙漠、丘陵、盆地、湖泊等工区勘探条件越显复杂.地震勘探过程中得到的地震记录混有各种随机干扰[1, 2].若随机干扰强度到达一定程度,必将影响后期地震资料的动校正速度的分析、静校正量的拾取等,最终影响数据成像效果,从而导致地震勘探工作者对地下地质结构及地质体的解释变得困难.
到目前为止,人们设计了多种不同的随机噪声的消除方法,例如:f-x域反褶积滤波方法、多项式拟合、径向预测滤波、反Q滤波[3~5]等等.这些方法在不同程度上解决了一些随机噪声的压制问题,但是仍然存在难以滤除强随机噪声的问题.最为经典的维纳滤波方法,由于其适用于任何平稳信号,并且能在一定程度上滤除含噪信号中的随机噪声而得到较为广泛的应用[6, 7].将维纳滤波应用在地震勘探中,在一定条件下可以滤除随机噪声,但当采集到的地震信号信噪比低到一定程度,维纳滤波处理过程中矩阵方程求解将会出现矩阵病态问题,使得求解滤波结果不精确,以至信号幅值产生衰减.
维纳滤波求解过程中出现的矩阵病态问题可以通过数据降维解决,主分量分析[8, 9](Principal Component Analysis,PCA)与Mercer核函数[10, 11]结合是一种较为理想的方法.主分量分析是一种线性降维方法,它把高维数据投影到低维子空间,是一种从高维数据空间提取数据特征的极好工具,目前应用于图像识别[12]、化学[13]、雷达目标识别[14]等各个领域.为了使主分量分析能提取出非线性的数据特征,在PCA方法的基础上加入Mercer核函数,称为核主分量分析(KPCA)[15~18].它的主要原理是将输入样本数据空间通过非线性映射到新的特征空间,使得数据在高维特征空间中线性可分,利用核函数代替内积计算,从而极大降低了计算的复杂度.
综合以上,本文提出一种基于核函数主分量的维纳滤波压制地震资料中强随机噪声方法(K-WPC),利用线性核函数对要处理的数据进行核变换,使其映射到高维数据空间,再利用主分量分析进行降维.核函数与主分量分析的优势在于:核函数在一定程度上减弱了滤除随机噪声时带来的幅值衰减问题,同时使得低信噪比条件下维纳滤波求解过程中出现的矩阵病态问题得到改善.此滤波方法对正演地震信号和实际地震信号做消噪处理,都得到令人满意的效果.
2 K-WPC方法的基本原理 2.1 核函数主分量维纳滤波经典维纳滤波中的维纳霍夫方程为[8]
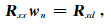
|
(1) |
其中Rxx、Rxd分别表示数据序列x的自相关函数E{xxT}、数据序列x和理想输出数据序列d的互相关函数E{dx},其中E表示数学期望.求得滤波因子序列wn为
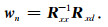
|
(2) |
为解决求解维纳滤波因子时Rxx-1易出现病态的问题,本文采取核主分量维纳滤波方法.K-WPC方法首先通过一个非线性核函数ϕ,把观测数据映射到更高维的特征空间中,然后在高维数据空间里采用标准的PCA方法降维并求解维纳滤波[18].这里PCA采用点积形式表示,利用Mercer核函数,新特征空间的点积可以直接在输入数据空间中计算,而不需要明确计算出非线性核函数ϕ.
一个数据样本集xi(i=1,2,…,N,xi∈Rn,N为样本数)在非线性映射ϕ的作用下映射到高维空间,即得到ϕ(xi).为了确保ϕ(xi)的均值为0,即保证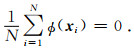

|
(3) |
C的特征值λ及其特征向量ν满足λv=Cv,其中λ1≥λ2≥…≥λn.
由于ν为ϕ(x1),ϕ(x2),…,ϕ(xN)的线性组合,所以一定存在一组相应的系数矩阵{αl},使得
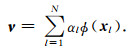
|
(4) |
将式(3)、(4)代入到λν=Cν中,有
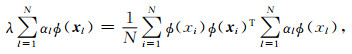
|
(5) |
可得

|
(6) |
现定义两矩阵:
(1)n×n矩阵K称为核矩阵,它的第ij位元素称为内积核,记作K(xi,xj),i,j=1,2,…,N.根据再生核空间理论,向量ϕ(xi),ϕ(xj)在特征空间中的内积<ϕ(xi),ϕ(xj)>可以用内积核K(xi,xj)表示,即K(xi,xj)=<ϕ(xi),ϕ(xj)>,而不用精确地计算映射到特征空间的函数ϕ(·),其中〈·〉表示内积.
(2)n×1矩阵α,第l个元素记作αl.对式(6)进行化简整理得:
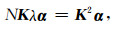
|
其中K2表示矩阵自身相乘,两端均有K,所以上式等同于:
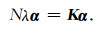
|
(7) |
由式(7)可知,α为核矩阵K的特征向量,与C的特征值λ对应.假设特征值是降序排列,即λ1≥λ2≥…≥λN,λZ为最小的非零值.为了确保协方差矩阵C的特征向量ν是归一化的,即νmTνm=1,m=1,2,…,Z.根据式(4)和式(7)可以得到νmTνm=1的等价归一化条件,αmTαm=1/λm,m=1,2,…,Z.计算ϕ(xi)向协方差矩阵C的Z个非零特征向量张成的特征空间V=[ν1,ν2,…,νZ]上的投影Pα,i,
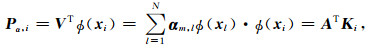
|
(8) |
其中Pα,i为ϕ(xi)的主分量,向量αm,l为核矩阵K中第m个特征值对应的特征向量αm的第l个系数,m=1,2,…,p,核矢量Ki=[K(xi,x1),K(xi,x2),…,K(xi,xN)]T,矩阵A=[α1,α2,…,αZ].
由上述过程可知,KPCA方法只需要在原空间通过核函数计算核矩阵,而不需要明确地计算出映射ϕ.通过定义核矩阵,主分量分析也可以当做是求解该核矩阵特征值和特征向量的问题.同时,在选取Z个特征值的时候,选取较大的特征值.因为原特征值越大,对重构时的贡献也越大,所以只需要选取原特征值中前大部分占绝对优势的特征值,使得维数Z小于原先矩阵维数,从而达到了降维的目的,以使矩阵的病态问题得到缓减.
利用线性核函数将地震数据映射到高维特征空间后,使用PCA方法得到所需要的主分量,利用所得到的主分量Pα,i,代替原始输入的地震信号xi.利用提取出的主分量Pα=[Pα,1,Pα,2,…,Pα,Z]和理想参考信号d=[d1,d2,…,dN]T,得到
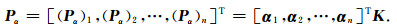
|
K-WPC算法的滤波因子求解表达式为
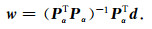
|
(9) |
综上所述,得到K-WPC算法的滤波表达式:
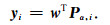
|
(10) |
采用K-WPC方法来解决地震勘探资料中的随机噪声消减问题.地震信号x(n)包含有效信号s(n)和随机噪声ω(n),即
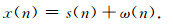
|
(11) |
为了消减地震信号中的随机噪声,针对低信噪比地震数据,基于噪声抵消的思想实现K-WPC对地震信号逐道进行处理.其实现过程如下:
首先,对第K道地震记录xK(n),构建特征信号向量:
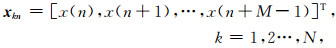
|
(12) |
M是特征信号向量长度,相应地有xkn=skn+ωkn.
第二,选择适合于地震信号的齐次核函数K(x,y)=(〈x,y〉)q,q∈IN*,以噪声作为维纳滤波的待处理信号,计算得到核矩阵K,每一个元素为K(ωi,ωK),i,j=1,2,…,N,并根据公式(8)计算第K道记录的主分量Pα, k.
第三,以观测数据xkn作为参考数据d,采用公式(9)求K-WPC算法的滤波因子wkn=(PαTPα)-1PαTxkn,利用主分量代替原待处理信号得到该道记录的维纳滤波ykn=wknTPα, k.
第四,从观测数据减去维纳滤波器的输出得到残差数据en应为待检测有效信号的估计ŝkn=xkn-ykn.
采用K-WPC消减地震勘探随机噪声,由于K-WPC经过核变换,在高维特征空间求解维纳滤波,提高了维纳滤波对输入空间非线性系统求解的能力,有利于更好地恢复地震信号;同时,通过结合核主分量分析降低数据维数,有效地解决了维纳滤波求逆过程中的病态问题.利用噪声抵消的思想实现K-WPC,有助于更好地防止信号在时域和频域的畸变.
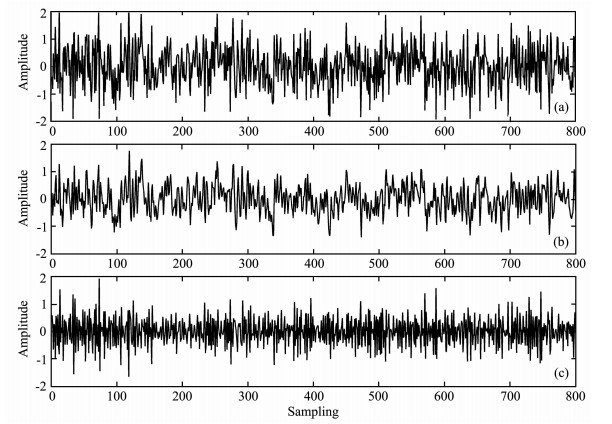
3 实验仿真 3.1 正演信号噪声处理实验本文在正演信号仿真实验时采用同源噪声为背景噪声,进行信号的滤波处理,同源噪声如图 1所示.
|
图 1 参考噪声 (a)随机白噪声;(b)同源白噪声;(c)噪声与同源噪声之差. Fig. 1 Reference noise (a) Random white noise; (b) The homologous noise; (c) The difference between the two noises. |
利用人工合成的共炮点记录进行试验.地震波是Ricker子波,偏移距为零,不考虑距离衰减.其中t0为双程垂直走时,取值为300ms,主频为30Hz,D为道间距,取值为50m,K为道序号,取值为40道,v为该反射同相轴相应的叠加波速,取值为1900m/s,所满足的双曲时距方程为:
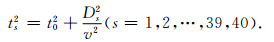
|
(13) |
将核主成分维纳滤波算法(K-WPC)应用于上述模拟地震记录.采样间隔Ts=1/500s,每一道数据均取801个采样点,雷克子波的主振幅度为2.5,滤波器阶数取12,线性核函数矩阵维数取12.
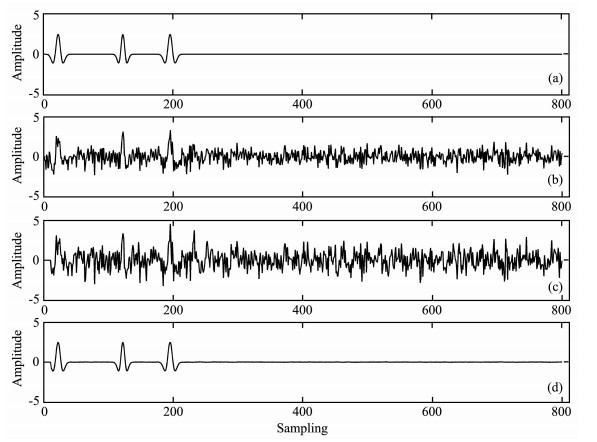
单道试验数据处理结果如图 2所示.滤波前SNR=-16.4622dB,维纳滤波后SNR=-11.2764dB,K-WPC滤波后SNR=10.655dB.多道正演信号处理结果见图 3.
|
图 2 单道正演信号 (a)模拟信号;(b)加噪信号;(c)维纳滤波结果;(d)K-WPC滤波结果. Fig. 2 Single modeling signal (a) Modeling signal; (b) Signal with noise; (c) The result of Wiener method; (d) The result of K-WPC filtering method. |
|
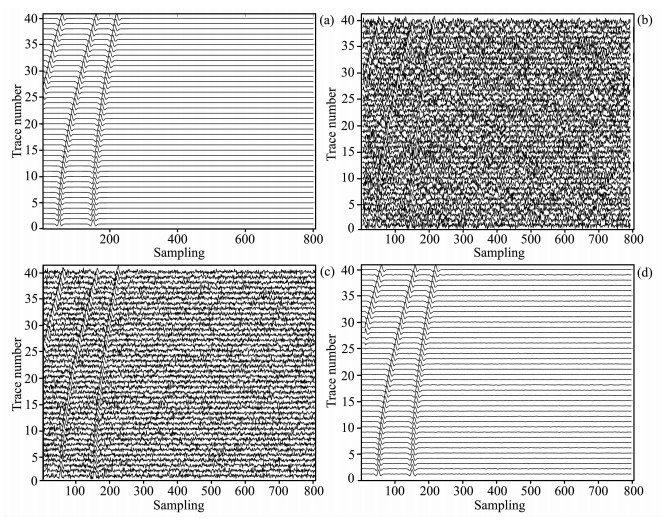
图 3 (a)多道正演信号;(b)加噪信号,SNR=-13.6739 dB; (c) Wiener滤波结果,SNR=-8. 6327 dB;(d) K-WPC滤波结果,SNR=8. 8781 dB Fig. 3 (a) Multitrack modeling signal; (b) Signal with noise; (c) The result of Wiener filtering method; (d) The resutt of K-WPC filtering method |
根据单道数据和多道正演信号的处理结果(如图 2,3所示)可知,维纳滤波方法对于强噪声环境下滤除随机噪声能力有限,输出结果中仍含有很强的随机噪声,输出数据同相轴不明显(如图 3c所示),信噪比只是稍稍提高,无法达到去噪处理的要求.对于K-WPC滤波结果,恢复出来的共炮点记录在宏观上可以很好地表现出原始记录中同相轴的位置,在其输出的信号中,随机干扰滤除较彻底,同时同相轴幅值保真性好(如图 3d所示).
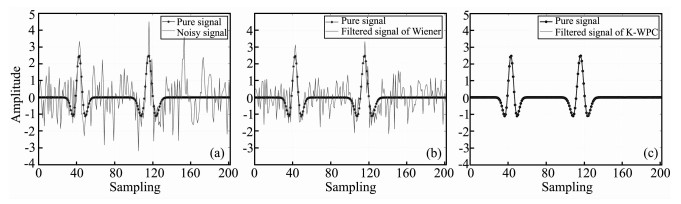
对第二道记录滤波前后含同相轴信号处的对比分析见图 4.混有强随机噪声的合成记录见图 4a,图 4a中标有星号的曲线为Ricker子波,信噪比较低,有效信号在波峰和波谷处因噪声干扰都存在较严重的畸变;对于传统维纳滤波结果,如图 4b所示,此方法只能滤除部分随机噪声,并且在有效信号处产生一定的畸变,且有效信号的峰值点和谷值点误差较大;K-WPC滤波的结果如图 4c所示,有效信号的峰值点和谷值点误差较小,几乎不存在毛刺现象,滤波后的记录接近于原始合成记录.可见,核主分量维纳滤波与传统的维纳滤波方法相比可以更好地消减随机噪声.在信号保幅和减少信号畸变方面得到较大改善.
|
图 4 第2道记录滤波前后对比 (a)原信号和含噪信号图;(b)原信号和维纳处理结果;(c)原信号和K-WPC方法处理结果. Fig. 4 The comparison of the 2th channel recording before and after filtering (a) Original record and Record with noise; ;(b) Original record and The result of wiener filtering method; (c) Original record and The result of K-WPC method. |
为了更好地说明K-WPC方法的适用性,将此方法应用于实际地震资料.
选取某炮区共炮点记录,如图 5a所示,该记录存在较强的随机噪声,同相轴不清晰,甚至被随机噪声截断.
|
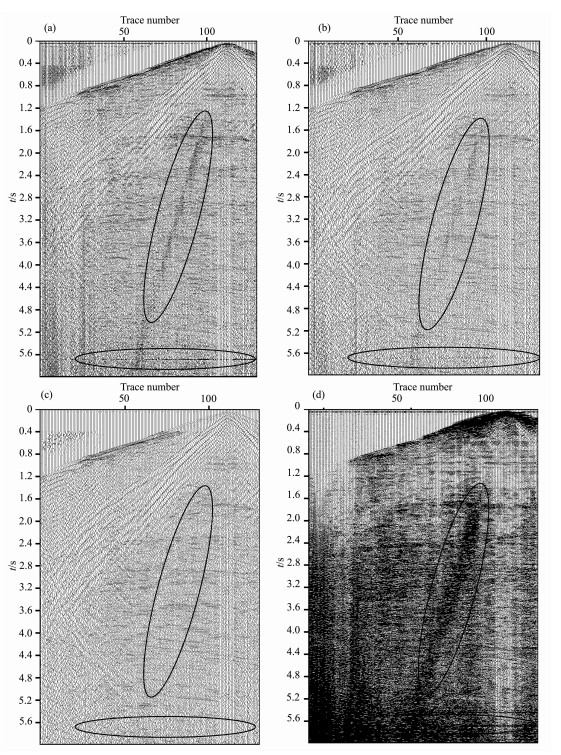
图 5 (a)原始实际地震数据资料;(b)Wiener方法处理实际地震数据的结果;(c)K-WPC方法处理实际地震数据的结果;(d)原始信号与K-WPC处理之后信号的差值 Fig. 5 (a) The practical seismic data; (b) The result of Wiener method for Practical seismic data; (c) The result of K-WPC for Practical seismic data; (d) The difference between the original and K-WPC |
分别采用传统维纳滤波和核主分量维纳滤波对图 5a共炮点记录进行处理,滤波效果分别如图 5b,5c所示.由于噪声干扰,传统维纳滤波方法使得数据矩阵求解不精确,随机噪声仍有残留.核主分量维纳滤波处理后,随机噪声消减效果比传统维纳滤波的效果令人满意.图 5d为原始信号与K-WPC处理之后信号的差值,差值图像中主要为被K-WPC滤除的随机噪声.可见,与一般维纳滤波相比,核主分量维纳滤波由于存在一系列核变换、主分量提取、降维处理使得计算得到的滤波因子较一般维纳方法的精准,最终表现为在消减随机噪声方面效果更为明显.从差值图像可以看出,K-WPC在消减随机噪声的同时,具有较好的保幅性.
4 结论将K-WPC算法应用于地震资料处理、理论研究与仿真实验,证明了该方法对地震资料中的随机噪声有很好的压制作用.将核函数与PCA算法相结合进行矩阵变换和降维,降低了在求解过程中产生病态矩阵的几率,使得矩阵求解精确,滤波性能明显提高.正演模型处理前后信噪比可以从-16. 4622dB左右提高到10.6550dB左右.同时,处理后信号同相轴连续性较好,有效信号的幅值衰减和畸变方面都较一般维纳方法改善很多.
| [1] | Ristau J P, Wooil M Moon. Adaptive filtering of random noise in 2D geophysical data. Geophysics , 2001, 66: 342-349. DOI:10.1190/1.1444913 |
| [2] | 胡天跃. 地震资料叠前去噪技术的现状与未来. 地球物理学进展 , 2002, 17(2): 218–223. Hu T Y. The current situation and future of seismic data prestack noise attenuation techniques. Progress in Geophysics (in Chinese) , 2002, 17(2): 218-223. |
| [3] | 崔若飞, 王辉. 多项式拟合技术在煤田地震勘探中的应用. 地球物理学进展 , 2000, 15(2): 47–54. Cui R F, Wang H. Application of polynomial fitting technique on coal seismic surveying. Progress in Geophysics (in Chinese) , 2000, 15(2): 47-54. |
| [4] | 董恩清, 刘贵忠, 张宗平. 自适应Kalman滤波反褶积的快速实现方法. 地球物理学报 , 2001, 44(2): 255–262. Dong E Q, Liu G Z, Zhang Z P. Fast implementation technique of adaptive Kalman filtering deconvolution via dyadic wavelet transform. Chinese J. Geophys. (in Chinese) , 2001, 44(2): 255-262. |
| [5] | Wang Y. Quantifying the effectiveness of stabilized inverse Q filtering. Geophysics , 2003, 68: 337-345. DOI:10.1190/1.1543219 |
| [6] | 刘沈衡. 维纳滤波法在重力资料解释中的应用. 有色金属矿产与勘查 , 1995, 4(1): 48–51. Liu S H. Application of the Wiener-filtration to the interpretation of gravity data. Geological Exploration for Non-Ferrous Metals (in Chinese) , 1995, 4(1): 48-51. |
| [7] | 崔晓杰.维纳滤波的应用研究[硕士论文].西安:长安大学, 2006. Cui X J. The application of Wiener filtering [Master's thesis] (in Chinese). Xi'an: Chang An University, 2006 http://cdmd.cnki.com.cn/Article/CDMD-11941-2006163502.htm |
| [8] | Sadasivan P K, Dutt D N. SVD based technique for noise reduction in electroencephalographic signals. Signal Process , 1996, 55: 179-189. DOI:10.1016/S0165-1684(96)00129-6 |
| [9] | Hyvärinen A, Karhunen J, Oia E.独立成分分析.周宗潭, 董国华, 徐昕等译.北京:电子工业出版社, 2007. Hyvärinen A, Karhunen J, Oja E. Independent Component Analysis. Zhou Z T, Dong G H, Hu D W, translation. Beijing: Publishing House of Electronics Industry, 2007 |
| [10] | Xu Q S, Liang Y Z. Monte Carlo cross validation. Chemometrics and Intelligent Laboratory Systems , 2001, 56: 1-11. DOI:10.1016/S0169-7439(00)00122-2 |
| [11] | Stordrange L, Libnau F O, Malthe-Sorenssen D, Kvalheim O M. Feasibility study of NIR for surveillance of a pharmaceutical process, including a study of different preprocessing techniques. Chemometrics , 2002, 16: 529-541. DOI:10.1002/cem.v16:8/10 |
| [12] | 范羚.独立分量分析及其在图像特征提取和消噪中的应用[硕士论文].合肥:安徽大学, 2003. Fang L. Independent component analysis and its applications of image feature extraction and denoising[Master, s thesis] (in Chinese). Ileiei: University of Anhui, 2003 http://cdmd.cnki.com.cn/Article/CDMD-10357-2003073086.htm |
| [13] | 姜晓东.主成分分析法在纳米KF/AI2O3催化剂制备中的应用[硕士论文].南京:南京工业大学, 2007. Jiang X D. Application of principal component analysis in preparation of Nano-KF/AI2O3 Catalyst [Master, s thesis] (in Chinese). Nanjing: Nanjing University of Technology, 2007 |
| [14] | 丛瑜, 肖怀铁, 付强. 基于核主分量分析的高分辨雷达目标特征提取与识别. 电光与控制 , 2008, 15(2): 31–38. Cong Y, Xiao H T, Fu Q. Target feature extraction and recognition for high-range recognition radar based on the KPCA method. Electronics OpLics & ConLrol (in Chinese) , 2008, 15(2): 31-38. |
| [15] | Müller K-R, Mika S, Ratsch G, Tsuda K, Scholkopf B. An introduction to kernel-based learning algorithms. IEEE Trans. NeuralNetworks , 2001, 12: 181-201. |
| [16] | Scholkopf B, Smola A J, Müller K-R. Nonlinear component analysis as a kernel eigen value problem. Neural Comput , 1998, 10: 1299-1319. DOI:10.1162/089976698300017467 |
| [17] | Zhang Z J, Lin Y H, Liu E R. Large static correction using a hybrid optimization method in complex terrain: some experience learnt from China. Journal of Seismic Exploration , 2005, 13(4): 337-352. |
| [18] | Li Y, Yang B J, Bada J, et al. Chaotic system detection of weak seismic signals. Geophys. J. Int. , 2009, 178: 1493-1522. DOI:10.1111/gji.2009.178.issue-3 |
 2010, Vol. 53
2010, Vol. 53


