一个地震波波形是由许多不同震相叠加而成,不同震相具有不同的运动学特征和动力学特征,代表不同性质的波动.研究从地震记录波形中分离出震相的波形,是震相分析的真正难点所在,也是机器自动识别震相的主要障碍[1].震相分离一般采用偏振滤波、相关滤波或偏移叠加等方法实现[1].地震波信号一般是非线性、非平稳信号,其实很多地球物理信号(如地磁信号、大气湍流、海洋面波及其产生的地脉动信号等)都可看成是非线性、非平稳信号[2],尤其是当地震信号被很强的噪声污染时,采用以上方法无法直接获得类似于震相的同轴对称的分量,因而也无法直接分离出固有震相.
Huang等[3]于1998年提出了一种非线性、非平稳信号分解方法---经验模态分解(Empirical Mode Decomposition EMD).该方法基于信号本身的时间尺度特征,把复杂的信号分解为有限个固有模态分量(Intrinsic Mode Function IMF)和一个余项,是一种自适应的信号处理方法,比依赖于先验基的傅里叶分析和小波分析等方法更适用于非线性、非平稳信号分析[3].目前,EMD广泛应用于信号处理领域[4~6]和二维图像处理领域[7~9],而且,也已被大量用于地震信号分析[10~15].EMD分解能够分离出信号数据驱动的固有模态分量,为地震信号的震相分析提供了一种潜在的手段.但由于EMD分解结果存在模态混叠问题[3, 4, 16],这使其应用受到限制:EMD中的模态混叠将导致地震信号分析中的震相混叠现象.所以,要将EMD分解应用于震相分析,首先须解决EMD的模态混叠问题.
解决模态混叠的方法很多,文献[17]将解决模态混叠的方法分成四类:瞬态测试方法[18, 19],辅助处理方法[20~22],改进IMF标准法[23]和改进包络均值法[16, 24, 25].也有多种方法的结合,如间歇模态筛选方法[26, 17]属于通过改进IMF标准、利用瞬态测试法的组合实现消除模态混叠.文献[27]提出了一种基于频带滤波获取单一模态分量的算法,该算法利用Fourier分析获取信号的主要频带,并确定带通滤波的频带范围,对带通信号进行EMD分解,并将带通分量的第一个IMF作为原始信号的IMF.该方法也是一种辅助处理方法,为克服经验模态混叠提供了非常好的思路,但仍有几个问题需要解决:(1)该算法只获得主要分量,不是一个完备的信号分解算法;(2)该算法在获得主要频带时需采用FFT算法确定带通滤波器参数,当信号频谱复杂时,或感兴趣信号频带被噪声覆盖时,很难找到合适的带通滤波器参数;(3)算法利用Fourier滤波器作为带通滤波器,从而将Fourier滤波器固有的边缘效应引入到EMD分解中,导致分离得到主要IMF端点失真,且很难获得趋势分量.
本文针对地震信号分析中的震相分离问题,试图通过改进频带滤波EMD算法,实现同轴向频率相近的振荡分量的自动分离,为震相分离、分析和判别提供新的工具.首先分析了EMD模态混叠存在的内在原因和以往的解决方法,理清了解决模态混叠的思路框架,进而提出了一种新的基于输入递归高通滤波的EMD算法,并将新算法应用于合成信号分解和天然地震信号分析.
2 EMD模态混叠为使希尔伯特变换得到的基本分量的瞬时频率具有物理意义,文献[3]按如下两个条件定义了IMF:(1)极值点数目与过零点数目相差不过1;(2)分量的局部极值点定义的上下包络的局部均值接近于零.第一个条件限定了IMF的振荡特性,第二个条件限定了IMF包络的对称性,从而保证该分量不包含其他模态分量.EMD算法认为,信号总由若干IMF和一个余项组成,它利用“筛选”算法,逐步从复杂信号中筛选出IMF分量,最后得到一个余项.
IMF的定义限定了振荡特性和单分量特性,但并没有限定IMF的窄带特性.模态混叠的表现形式是相邻或相间的模态中出现了相似或相同的模态分量.从地震信号处理的角度看,模态混叠表现为一个IMF中出现两个或两个以上的主周期分量.从不同角度究其原因,可得出不同结论.例如包络中的“骑墙”现象会导致模态混叠,噪声易导致模态混叠,瞬态信号也会导致模态混叠[4].自然物理事件的间歇出现与IMF概念和EMD算法不具备间歇特性之间的矛盾是EMD模态混叠的内在原因[17].
EMD分解通过由信号局部极值点构成的包络进行筛分,实现完全数据驱动的信号分解.EMD分解的数据驱动特性,对信号来讲是自适应性的.但分析发现,如果数据中包含2类或2类以上不同性质模态的极值点,则EMD会不加鉴别地把由这些不同类型极值点所决定的模态分量筛分出来,从而导致模态混叠.所以,数据驱动特性是一把双刃剑:一方面,数据驱动特性可避免主观干扰,使分离信号“固有”模态分量成为可能;另一方面,当信号中存在噪声[20, 21]或间歇模态[17]时,数据驱动特性使EMD盲目将信号中的由局部噪声或间歇信号极值点所决定的模态分量筛分出来,从而导致模态混叠.
3 解决模态混叠的思路 3.1 常见方法分析本节将从算法要素的角度,对这些算法进行分类,进而提出改进思路.一个算法一般包含两类要素:信号和操作.信号是操作的基本对象.一个算法通常由一个或多个操作构成,而每个操作又具有一个或多个输入和输出信号.各操作构成了算法的操作序列,操作序列的输入和输出信号构成了算法的信号流.
EMD分解包含三类基本操作:Sifting、IMF条件判断和EMD终止判断.这三类操作及其输入、输出信号流,可构成EMD分解的基本流程.如果从EMD算法的一些要素入手,并对这些要素进行修正,则本质上可看成是对EMD算法的要素流程图的修正.例如:
(1)改进包络均值方法[16, 24, 25]从Sifting算法内部的包络环节进行改进;间隙模态分解算法则对EMD终止条件进行改进,减小虚假模态的数目[17];这些方法主要针对EMD算法内部的操作和信号流进行修正,可将这类方法称为内部要素改进法.
(2)瞬态测试法[18, 19]关注IMF中的局瞬分量,并通过改善IMF的上下限频率来防止模态混叠;改进IMF标准法[23]和间歇经验模态分解[17]也是从改进IMF的标准或定义,达到消除模态混叠的目的.这类方法无法解决EMD频率分辨率较差的缺点,并且还加入了人为干扰.鉴于它们从EMD筛分输出IMF的标准入手进行修正,不妨称之为输出要素修正法.由于该类方法采用了残余分量递归筛分,所以是完备的算法.算法框图如图 1所示,其中IMF表示筛分得到的IMF,RES表示与之对应的残余分量.

|
图 1 完备的输出修正法示意图 Fig. 1 Flow diagram of complete method by improving output |
(3)预滤波[20]、频带预处理方法[27]和白噪声辅助法[21]关注噪声或不同信号成分对IMF的影响,这类算法认为,导致EMD模态混叠的是输入信号不能适应EMD算法.EMD算法本身是无需改进的,只需改善输入信号即可.差分与累积求和方法[28]则认为:用差分信号求IMF,更容易提取间歇的IMF.鉴于以上算法将EMD算法作为一个整体考虑,通过改变EMD的输入来改善EMD的输出,所以,不妨称之为输入要素修正法.由于该类方法对不同的分量独立处理,不是递归筛分,所以它不是完备的分解.该类算法示意框图如图 2所示,其中IMF表示筛分得到的IMF,RES表示与之对应的残余分量.

|
图 2 不完备的输入修正法示意图 Fig. 2 Flow diagram of incomplete method by improving input |
一般可从两个途径提出解决EMD模态混叠问题的思路:(1)直接从实际问题出发,找出模态混叠问题发生的要素,进而从要素出发,提出解决模态混叠问题的方法;(2)从算法的各要素出发,分析各要素对模态混叠的影响,进而提出改进思路.上文按EMD改进要素将改进算法分为三类,从改进要素的组合来看,解决模态混叠的潜在方法至少包括以下7类:输入、输出、内部、输入+输出、输入+内部、内部+输出和输入+内部+输出.若考虑残余分量是否递归筛分,则潜在的可选方法更多.
3.3 EMD的完备性EMD算法具有很强的信号自适应性,可筛分出信号中由极值点决定的模态分量.预滤波法[20]和频带滤波法[27]将高频、低频或低能量成分看成噪声,通过滤波方法剔除由噪声决定的极值点,从而改善EMD输出,解决模态混叠问题.但由于输入信号不是原始信号,所以很多细节无法得到.在震相分析、震源识别、故障诊断、数据压缩等情况下,这些细节恰恰又是研究者关心的内容.特别是在震相分析中,当待分析的地震波形所含噪声的振幅或强度远远大于地震波信号的振幅或强度时,舍弃极少量噪声信息都可能使地震波震相严重失真,甚至无法判读.所以完备的EMD分解对地震信号震相分析非常重要.
频率是模态的一种重要属性,通过频率将不同模态分量预分离,再用EMD进行筛分是一种可行的方案.利用滤波方法构建完备的EMD,需要具备两个条件:完备的带通预滤波、完备的输出.前者可通过递归高通滤波实现,后者可借助残余分量的递归筛分实现.基于以上分析,下文提出基于递归高通滤波和输出递归筛分修正法的EMD算法.
4 递归高通滤波+递归筛分修正法 4.1 算法框架本节通过对输入信号的递归高通滤波和输出残余分量的递归筛分实现完备的EMD分解:信号通过一级高通滤波,被分解成一个高频分量和一个低频分量,所得到的低频分量作为下一级高通滤波器的输入,各级滤波器的截止频率逐级减小,从而实现等效的带通滤波,如图 3所示.

|
图 3 递归高通滤波示意图 Fig. 3 Flow diagram of recursive high-pass filters |
第一个高频分量输入到EMD进行细筛分,获得IMF和残余分量,残余分量与下一级高频分量叠加得到新的EMD输入信号,如此实现高频分量的递归分解.由于EMD筛分本身就是等效带通滤波,通过一次筛分就显著地筛分出频率相近的一类极值点,筛分后残余分量中凸显出来的极值点之间的距离一般与IMF极值点之间的距离存在显著差别,残余分量中包含的极值点属于后续的IMF.所以,本文试图通过将筛分后的残余分量直接添加到对应低频信号,以避免后续筛分的IMF产生残缺的现象.如果把信号的高频分量或低频分量当作噪声,则一方面可将前面的高频分量直接输出为IMF,另一方面可将最后的几个高频分量直接输出为残余分量.完整的改进EMD算法如图 4所示.

|
图 4 完备的输入修正+递归筛分法框图 Fig. 4 Flow diagram of complete method by improving input and recursive sifting |
本文采用递归高通滤波器实现等效带通滤波器.为减小带通滤波器引起信号端点频率泄漏,并实现任意等效带通滤波器,笔者采用Park-McClellan算法[29].Park-McClellan算法采用remez交换算法和cheby-shev近似理论设计滤波器,使实际的频率响应拟合期望频率达到最优.从实际和理想频率响应之间的最大误差最小化的观点看,Park-McClellan算法设计的滤波器是最优的,因此也称为最优滤波器.采用MATLAB中的remez函数实现最优滤波器的设计.remez函数原型为
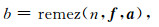
|
(1) |
其中,n为滤波器阶数,f为滤波器期望频率特性归一化频率向量,是范围为0~1的递增向量;a为滤波器期望频率特性的幅值向量,向量a与向量f长度相等,且为偶数.n根据信号的长度取值,要求为偶数,且长度小于信号长度的1/3.f=[0 fe fe+fw 1];fe为归一化边界频率;fw为过渡带宽度;a=[0 0 1 1].各级滤波器中的a相等,fe逐级递减.
4.3 参数选择方法在实际问题中,参数fe直接影响高通滤波性能,从而影响等效带通滤波的频率响应,最后也会影响EMD的结果.郭淑卿[27]通过FFT频谱分析获得的主要频带来确定带通滤波器参数,但并没有给出具体的算法.最直观的做法是将谱峰的中点频率作为递归滤波器边界频率.但笔者通过统计EMD分解高斯噪声得到IMF的最大经验周期的变化规律发现,最大经验周期在对数坐标系下对IMF序号近似服从线性关系[30];Flandrin等[31]则通过统计分析EMD分解高斯噪声得到IMF发现,IMF极值点数目在对数坐标下对IMF序号也近似服从线性关系.所以,将谱峰对应的频率映射到对数坐标下,用对数坐标下的谱峰之间的中点频率作为递归滤波器边界频率更合适.另外,当主频率之间距离较大时,如果直接在对数坐标系下求中点,仍然无法得到理想的结果,此时需要在中间插入附加的边界参数.所以,本文给出如下fe的选择算法:
(a)计算信号的FFT频谱,获得主要谱峰的频率,记作fk,其中k=1,2…,K,且fk随k的增加而减小.归一化频率为
(b)求对数序列lfk=log2(1/fk),并在序列起始端插入lf0=0,序列末尾添加一个大小为lfK+1=lfK+1的值.若lfk-lfk-1较大,则表明两谱峰间的频带较宽,须在中间插入若干边界频率.设λ为一常数,表示两谱峰间最大频带在对数坐标下跨度的两倍值,一般取λ∈[2, 3].若(lfk-lfk-1)>λ,为保持(lfk-lfk-1)<λ/2,可在lfk和lfk-1间均匀插入
在感兴趣信号的FFT频带不明显时,可采用二进带通滤波算法筛分IMFs,此时,第k级高通滤波器的边界频率归一化幅度为fek=1/2k.过渡带宽度会影响频率在尺度上的衰减速度,为了与二进带通滤波器相对应,可取
在递归滤波时,需要解决递归的终止问题.假设时间序列长度为L,则在离散时间信号分析中,归一化频率的最大频率为fmax=fs/2,最小频率为fmin=2fs/L,递归滤波器参数fek的取值范围为fek∈(fmin/fmax,1).所以,当fek≤4/L时,理论上递归滤波就可停止.在实际应用中,也可判断图 4中低频分量是否满足EMD终止条件来确定.另外,也可根据感兴趣频率成分的频率来确定递归的终止条件,即当fek小于感兴趣成分的频率下限,递归就终止.
5 仿真试验分析 5.1 合成信号分析 5.1.1 信号准备若采样频率fs=1000Hz,构造如下信号:

|
(2) |
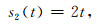
|
(3) |

|
(4) |

|
(5) |

|
(6) |

|
(7) |
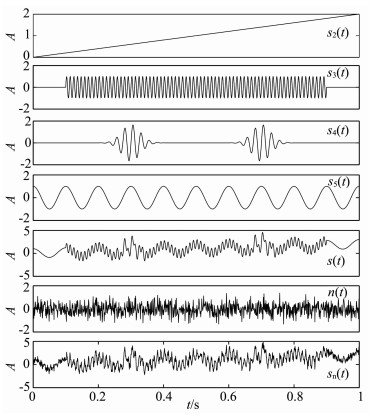
其中,f1=40Hz,f2=90Hz,f3=10Hz,a=400π.如果|t|≤0.15,rect1(t)=1,否则rect1(t)=0;如果0.1≤t≤0.9,rect2(t)=1,否则rect2(t)=0. n(t)为一高斯白噪声,sn(t)=n(t)+s(t).s1(t)的波形如图 5所示,其他各仿真信号如图 6所示.

|
图 5 s1(t)的波形图 Fig. 5 Waveform of s1(t) |
|
图 6 仿真信号波形图 Fig. 6 Waveforms of simulated signals |
对s(t)进行EMD分解,得到结果如图 7所示.其中,imf1中0.1~0.9s间主要体现了s3(t),理想的模式是在其他时间段,幅度应近似等于0.但在0~0.1s和0.9~1s两个时段都出现了振幅和imf1相当,频率却远远小于imf1的振荡波形.可见,得到的第一个IMF就发生了严重的模态混叠.受imf1中模态混叠的影响,后面筛分的结果不确定性增加.基于分解的完备特性,在imf1中多余出现的部分必然由其他IMF贡献,所以,在imf3中,对应时刻发生模态缺损现象.类似的现象也发生在imf2中:如果把imf2与s4(t)对应,则0~0.2s,0.4~0.6s,0.8~1s三个时段的幅度应近似等于0,但是结果却出现了振幅相当的振荡波形.

|
图 7 EMD对s(t)的分解结果,其中imfn表示第n个IMF,res表示残余分量,下同 Fig. 7 Results of s(t) from EMD, in which, imfn represents the nth IMF, and res represents the remainder (the following is the same) |
对sn(t)进行EMD分解,得到结果如图 8所示.由于噪声的频谱较宽,覆盖在sn(t)表面的第一层极值点对应的频率高于仿真模态分量中s3(t)的频率,所以imf1主要是噪声,imf2与s3(t)对应.但是imf2与s3(t)波形的相似度已经很小,波形断断续续被极值点间距更小的噪声模态所隔断.imf2中缺损的本属于s3(t)的波形在下一次筛分中又污染了imf3,这样的混叠与缺损一层一层地重复出现.
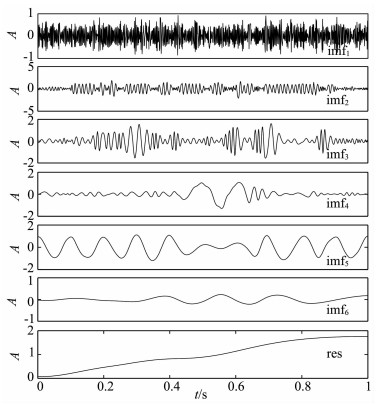
|
图 8 EMD分解sn(t)的结果 Fig. 8 Results of sn(t) from EMD |
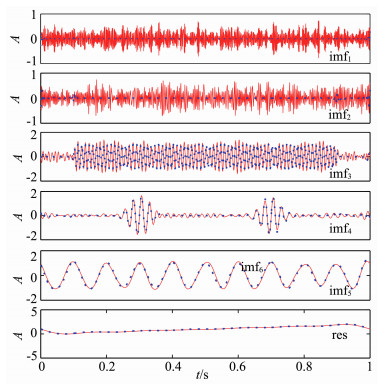
由于郭淑卿[27]提出的频带滤波筛选法没有给出带通滤波边界参数的选择方法,所以,笔者用本文提出边界参数选择法进行选择,并给出频带滤波EMD分解结果.用FFT确定谱峰位置后,计算递归滤波器的边界参数即为频带滤波器参数.对s(t)和sn(t)进行频带滤波EMD分解,得到结果见图 9.
|
图 9 频带滤波EMD对s(t)(蓝色虚线)和sn(t)(红色实线)的分解结果 Fig. 9 Results of s(t) (blue broken lines) and sn(t) (red solid lines) from bandpass EMD |
由于本文参数选择方法插入了一个边界参数,所以在高频段多出一个IMF,频率最低的残余分量直接输出,不参与筛分.试验结果中,分别对s(t)和sn(t)分解得到的imf3~imf5和res基本重合,对应于s2(t),s3(t),s4(t)和s5(t),说明噪声对分解结果影响较小,各层分解独立,避免了EMD分解中模态混叠效应的层间累积现象;imf5和res的两端严重变形,说明基于频带滤波的EMD算法对FFT滤波的端点效应较敏感.
5.1.4 改进EMD分解结果分析用FFT确定谱峰位置后,计算递归滤波器的参数.直接用递归高通进行滤波得到的结果y1~y6如图 10中蓝色虚线所示;对s(t)进行递归分解得到imf1~imf5和一个残余分量,结果分别如图 10中红色实线所示.由于直接用递归高通滤波得到的y1和y2幅度很小,所以分离得到imf1和imf2的幅度也很小.s2(t),s3(t)和s4(t)主要出现在y3,y4和y5,极值点较好地分离开.算法利用Park-McClellan算法和递归方案较好地克服了端点效应,获得了与原始信号非常逼近的趋势项.用Park-McClellan算法并没有按频率高低实现完全频带分离的等效带通滤波,只是抑制了低频分量的幅度,突出了高频分量极值点对波形的影响,因而有效地分离了高频极值点和低频极值点.

|
图 10 s(t)的递归高通结果(蓝色虚线)与改进EMD分解结果(红色实线),其中,yn表示第n个递归高通分量 Fig. 10 Results of s(t) from recursive high-pass filter (blue broken lines) and improved EMD (red solid lines), where yn represents the nth recursive high-pass component |
对sn(t)进行递归分解得到imf1~imf6和一个残余分量,结果分别见图 11中实线;直接用递归高通进行滤波得到的结果y1~y6见图 11中虚线.

|
图 11 sn(t)的递归高通结果(蓝色虚线)与改进EMD分解结果(红色实线) Fig. 11 Results of sn(t) from recursive high-pass filter (blue broken lines) and improved EMD (red solid lines) |
试验结果表明:对含噪信号和无噪信号进行改进EMD筛分得到的IMF基本克服了模态混叠;试验结果也证实,由于EMD筛分本身就是等效带通滤波,筛分后残余分量中凸显出来的极值点之间的距离一般与IMF极值点之间的距离存在显著的差别,通过回收Park-McClellan算法滤波得到带通信号中的低频分量,以避免后续筛分的IMF产生残缺的现象是可行的;算法利用Park-McClellan算法和递归方案较好地克服了端点效应,获得了与原始信号非常逼近的趋势项.
5.2 天然地震信号分析本例将递归高通滤波+递归筛分的EMD算法用于分解喀什地震台中记录到的一个地震信号.地震发生在2003-07-2410:10,震中距喀什地震台121km,采样频率为25Hz.图 12给出了原始波形及其频谱图.图中显示原始地震信号中夹杂着多组高频干扰,地震信号波形和频谱被完全淹没,运动学特征和动力学特征分析都较困难.

|
图 12 地震信号的原始波形(a),频谱(b),和频谱局部放大图(c) Fig. 12 The wave form (a), frequency spectrum (b) and amplified frequency spectrum (c) of the original seismic record |
地震波所描述的质点振动方式非常复杂,但都可看成由系列相对简单的振动叠加而成.改进EMD算法的理想结果是将信号分解成经验周期范围互不重叠、包含单个经验周期谱峰、质点运动相对简单的振荡分量.文献[17]用经验周期来判断模态是否混叠.实际上,经验周期的谱峰与地震信号分析中的主周期的物理含义相近.所以下文用经验周期谱来判断是否存在震相(模态)混叠是可行的.为方便观察模态是否存在混叠,将经验周期坐标设置为对数坐标.
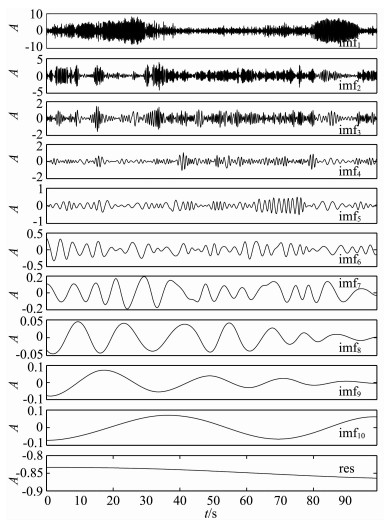
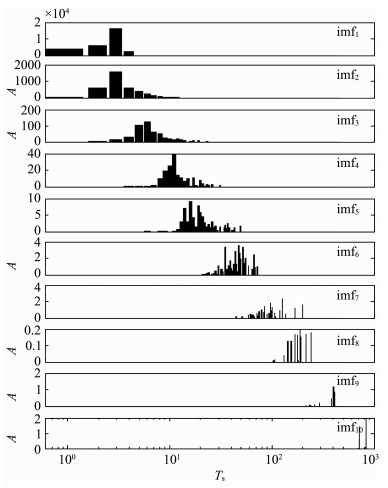
分别用EMD、频带滤波EMD和二进递归高通滤波EMD对地震信号进行分解,并计算所得IMF的经验周期谱[17].图 13为EMD分解结果,图 14是分解结果的经验周期谱.图中显示,相邻模态分量的经验周期谱混叠严重,无法进一步应用地震信号.
|
图 13 EMD分解地震信号的结果 Fig. 13 Results of seismic signal from EMD |
|
图 14 EMD分解结果的经验周期谱 Fig. 14 Empirical period spectrum of the IMFs from EMD |
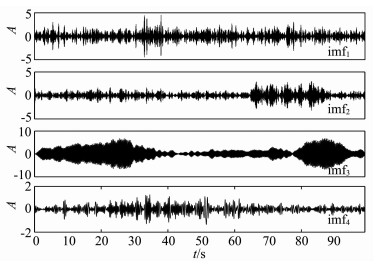
从图 12地震信号的频谱图中可看出,在4.7Hz处出现一个能量较高的频带,在10Hz和12Hz处附近也有能量较高的频带.基于此,依据文献[27]中的方法,确定3.8Hz、7Hz和11Hz为边界频率,设计四个带通滤波,并对各带通分量进行EMD分解,将筛分得到的第一个IMF作为频带滤波EMD的输出,结果如图 15所示.显然,由于高频的频带能量远远超过低频地震信号的能量,感兴趣的地震信号的频带无法判断,因而,用频带滤波EMD方法得到的IMF不是地震信号振荡波形.在这种情况下,本文提出的基于FFT频谱的递归参数选择方法也失效,所以,下面尝试采用二进递归滤波方式计算边界参数.
|
图 15 地震信号的频带EMD分解结果 Fig. 15 Results of seismic signal from bandpass EMD |
图 16和图 17分别给出了二进递归滤波EMD的分解结果和经验周期谱.实验结果表明,地震信号被分解成9个模态分量和一个残余分量,各模态分量的经验周期谱基本不混叠.每个分量的周期谱比较窄,基本形成单峰状态.每个分量包含一个主周期,方便进一步提取地震信号的运动学特征和动力学特征.
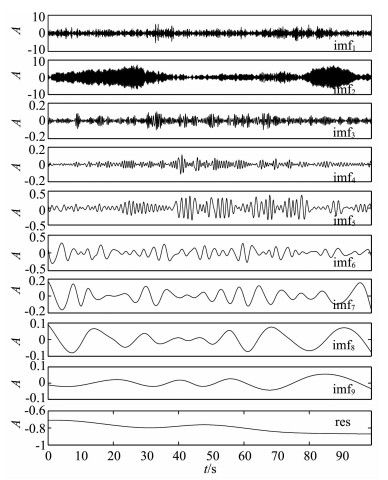
|
图 16 改进算法分解地震信号的结果 Fig. 16 Results of seismic signal from improved EMD |
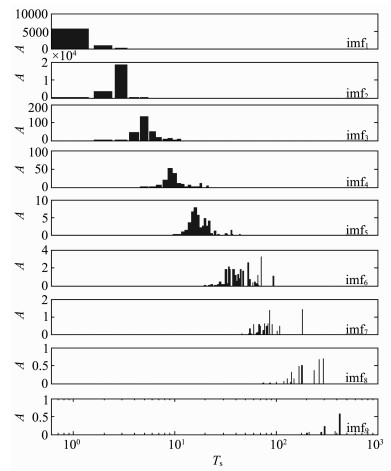
|
图 17 新算法分解结果的经验周期谱 Fig. 17 Empirical period spectrum of the IMFs from improved EMD |
将采样周期记为Ts,在图 16中,imf3为经验周期范围为3~7Ts,谱峰处于5Ts,即主周期为0.4s,频率为2.5Hz的一个同轴向振荡分量.在8.12s处发生一个大幅度振荡,表明该处为P波初至点.imf4为经验周期范围为7~12Ts,谱峰处于9Ts,即主周期为0.72s,频率为1.39Hz的一个同轴向振荡分量.一般S波周期和振动幅度都大于P波,结合imf3和imf5的振幅和相位变化,可初步判断在imf4的22.04s处开始发生S波.Ts-Tp=13.92s,由此可估算震中距为123.05km,与实际震中距121km仅差2.05km.在imf3的11.96s、14.64s和17.76s处出现三个振幅较第一个P波振幅小的震相,在imf4的对应时刻也出现三个振幅较小首尾连接的震相.imf5为经验周期集中在14~21Ts,谱峰位于17Ts,即主周期为1.36s,频率为0.74Hz的一个同轴向振荡分量.在imf5中第38s附近有一个频散明显的面波波形.
5.3 讨论 5.3.1 关于地震信号的模态混叠模态混叠的表现形式是相邻或相间的模态中出现了相似或相同的模态分量.从地震震相分析的角度看,模态混叠表现为一个IMF中出现两个或两个以上的主周期,两个相邻或者相间的模态分量的主周期过分接近,造成频谱发生交叠;也就是,同一个震相被分割到两个不同的分量中,不同频率的震相出现在一个模态分量的同轴向.纵波的周期比横波的周期小,面波的周期最大;纵波的振幅小于横波,面波的振幅最大(深震除外).因而,理想的地震信号EMD分解结果,应该是每个IMF包含一个主周期,有三个分量的主周期与纵波、横波和面波的主周期分别对应.而且各分量的经验周期谱互不交叠,频率相近的震相出现在同轴向.本文算法将纵波、横波和面波分解到三个单主周期的IMF中,为震相分析提供了便利.
5.3.2 关于震相的数据驱动特性EMD数据驱动特性是一把双刃剑,不加鉴别地筛分出不同类型的极值点构成的模态分量是导致EMD模态混叠的主要原因.由于各种不同性质的地震波先后被仪器记录下来,而且,同时到达的震相还相互重叠,尤其是地震波记录被大量未知震源的震波污染,直接用EMD分解时,EMD无法鉴别极值点类型.当信号被带通滤波后,信号局部极值点具有与带通滤波器相近的频率性质,带通滤波后的EMD就能充分发挥数据驱动的性质,将该带通范围内的IMF筛分出来.
如前所述,数据驱动特性也使IMF包含了大量地震波的动力学特性和运动学特性.由于传播速度不同,震源发出不同频率的震动波,会先后到达震波接收仪器.仪器接收的信号经改进EMD分解,频率相近的地震波会出现在同一IMF的同轴向.利用这些思路和方法,一方面可确认过去不为人所注意的震相,找到理论上证明存在,但实际记录中尚未发现的震相;另一方面,通过研究同一个震源发出的纵波-横波和面波的不同直达波、反射波所表现的,具有相近的频率和振幅变化规律的振荡分量,还可获得地震波的动力学特性和运动学特性.
6 结论本文试图通过改进频带滤波EMD算法,克服EMD模态混叠问题,进而为解决地震信号分析中的震相分离问题提供新思路.主要结果和结论如下:
(1)提出了基于要素的算法分析与改进方法,并用于解决EMD模态混叠问题,进而提出解决模态混叠的思路和潜在方法.
(2)针对地震信号震相分离问题,提出了基于输入递归高通滤波和残余分量递归筛分的EMD算法,并提出了感兴趣信号频带明显和不明显两种不同情况下,递归高通滤波器参数的确定方法.
(3)用仿真信号验证了在频带明显时,本文算法与传统EMD相比,可克服模态混叠问题,与频带滤波EMD方法相比,可克服滤波算法的端点效应对IMF端点的影响,并获得更好的趋势项.
(4)将改进EMD算法应用于地震信号分析中,证实了二进带通选择方法在感兴趣信号频带不明显时的有效性.算法较好抑制了噪声极值点对固有震相的影响,其分解结果明显优于传统EMD和频带滤波EMD.通过分析各IMF内各震相的幅度、相位的相关性和IMF间各震相的幅度、相位的相关性,确定了地震信号的P波、S波和面波震相,并较正确地估算了震中距离.
| [1] | M.巴特.地球物理学中的谱分析.郑治真等.北京:地震出版社, 1978. Bath M. Spectral Analysis in Geophysics (in Chinese), Translated by Zheng Z Z, et al. Beijing: Seismological Press, 1978 |
| [2] | 赵鸿儒, 孙进忠, 唐文榜, 等. 全波震相分析. 北京: 地震出版社, 1991 . Zhao H R, Shun J Z, Tang W B, et al. Wave Seismic Phase Analysis (in Chinese). Beijing: Seismological Press, 1991 . |
| [3] | Huang N E, Shen Z, Long S R, et al. The empirical mode decomposition and the Hilbert spectrum for nonlinear and non-stationary time series analysis. Proc. R. Soc. Lond , 1998, 454: 903-995. DOI:10.1098/rspa.1998.0193 |
| [4] | Huang N E, Zheng S, Long S R. A new view of nonlinear water waves: the Hilbert spectrum. Annu. Rev. Fluid Mech , 1999, 31: 417-457. DOI:10.1146/annurev.fluid.31.1.417 |
| [5] | Boudraa A O, Cexus J C. EMD-Based Signal Filtering. IEEE Transactions on Instrumentation and Measurement , 2007, 56(6): 2196-2202. DOI:10.1109/TIM.2007.907967 |
| [6] | Hadjileontiadis L J. A novel technique for denoising explosive lung sounds empirical mode decomposition and fractal dimension filter. Engineering in Medicine and Biology Magazine. IEEE, Jan.-Feb. 2007 26(1):130~39. |
| [7] | Nunes J C, Guyot S, Delechelle E. Texture analysis based on local analysis of the bidimensional empirical mode decomposition. Machine Vision and Applications , 2005, 16: 177-188. DOI:10.1007/s00138-004-0170-5 |
| [8] | Liu Z, Peng S. Boundary processing of bidimensional EMD using texture synthesis. IEEE Signal Process, Lett , 2005, 12(1): 33-36. DOI:10.1109/LSP.2004.839700 |
| [9] | Linderhed A. Compression by image empirical mode decomposition, in proc. IEEE Int. Conf. Image Processing , 2006, 1: 553-556. |
| [10] | 张郁山.希尔伯特一黄变换(HHT)与地震动时程的希尔伯特谱一方法与应用研究研[博士论文].北京:中国地震局地球物理研究所, 2003. Zhang Y S. HHT and Hilbert spectrum earthquake ground motion-Study of methods and applications [Ph. D. thesis] (in Chinese). Beijing: Institute of Geophysics, China Seismological Bureau, 2003 http://cdmd.cnki.com.cn/Article/CDMD-85401-2004137815.htm |
| [11] | 张义平.爆破震动信号的HHT分析与应用研究[博士论文].长沙:中南大学资源与安全工程学院, 2006. Zhang Y P. HHT Analysis of blasting vibration and its application [Ph. D. thesis] (in Chinese). Changsha: School of Resources and Safety Engineering, 2006 |
| [12] | 曹晖, 曹永红. HH变换在地震动信号分析中的应用. 重庆大学学报 , 2008, 31(8): 922–927. Cao H, Cao Y H. Application limitation of the Hilbert-Huang trans!orm to earthquake ground motion analysis. Journal of Chongqing University (in Chinese) , 2008, 31(8): 922-927. |
| [13] | 段生全, 贺振华, 黄德济. HHT方法及其在地震信号处理中的应用. 成都理工大学学报(自然科学版) , 2005, 32(4): 396–400. Duan S Q, He Z H, Huang D J. Application of the Hilbert-Huang transform to the analysis of seismic signal. Journal of Cheng Du University of Technology (Science & Technology Edition) (in Chinese) , 2005, 32(4): 396-400. |
| [14] | Huang N E. A new spectral representation of earthquake data: Hilbert spectral analysis of station. Bulletin of the Seismological Society of America , 2001, 5: 1310-1338. |
| [15] | Zhan G R. Hilbert-Huang transform analysis of dynamic and earthquake motion recordings. ASCE , 2003, 8: 861-875. |
| [16] | Rilling G, Flandrin P, Goncalves P. On empirical mode decomposition and its algorithms. EEE-EURASIP Workshop on Nonlinear Signal and Image Processing, NSIP-03, Grado (I). 2003. http://www.oalib.com/references/19337330 |
| [17] | 钱昌松, 刘代志, 刘志刚, 等. 间歇信号的经验模态筛选方法. 第二炮兵工程学院学报 , 2009, 1(23): 53–62. Qian C S, Liu D Z, Liu ZG, et al. A novel sifting method for empirical mode decomposition of intermittent signal. Journal of Second Artillery Enginering University (in Chinese) , 2009, 1(23): 53-62. |
| [18] | 禹丹江, 任伟新. 信号经验模式分解与间断频率. 福州大学学报 , 2005, 33(5): 638–642. Yu D J, Ren W X. Signal empirical mode decomposition and intermittency frequency. Journal of Fuzhou University (in Chinese) , 2005, 33(5): 638-642. |
| [19] | 宋立新, 王祁, 王玉静, 等. 具有间断事件检测和分离的经验模态分解方法. 哈尔滨工程大学学报 , 2007, 28(2): 178–182. Song L X, Wang Q, Wang Y J, et al. Empirical mode decomposition method with intermittency test and separation. J ournal of Harbin Engineering University (in Chinese) , 2007, 28(2): 178-182. |
| [20] | 赵进平. 异常事件对EMD方法的影响及其解决方法研究. 青岛海洋大学学报 , 2001, 31(6): 805–814. Zhao J P. Study on the effects of abnormal events to empirical mode de-composition method and the removal method for abnormal signal. J ournal of Ocean University of Qingdao (in Chinese) , 2001, 31(6): 805-814. |
| [21] | Wu Z, Huang N E. Ensemble Empirical Mode Decomposition: a Noise-assisted Data Analysis Method. Centre for Ocean-Land-Atmosphere Studie , 2004, 173. |
| [22] | Ryan D, James F K. The use of a masking signal to improve empirical mode decomposition. ICASSP 2005 , 2005, 5: 485-488. |
| [23] | Xuan B, Xie Q W, Peng S L. EMD sifting based on bandwidth. IEEE Signal Processing Letters , 2007, 14(8): 537-540. DOI:10.1109/LSP.2007.891833 |
| [24] | Huang Y P, Li X Y, Zhang R B. A research on local mean in empirical mode decomposition. Lecture Notes in Computer Science , 2007, 44(89): 125-128. |
| [25] | 李雪耀, 黄永平, 张汝波. 一种基于支持向量回归机的经验模态分解方法. 哈尔滨工程大学学报 , 2007, 28(7): 779–784. Li X Y, Huang Y P, Zhang R B. Empirical mode decomposition based on support vector regression machines. J ournal of Harbin Engineering University (in Chinese) , 2007, 28(7): 779-784. |
| [26] | 钱昌松, 刘志刚, 胡重庆, 等. 一种新的经验模态分解及其应用初探.地球物理探测与应用. 西安: 西安地图出版社, 2007 : 201 -205. Qian C S, Liu Z G, Hu C Q, et al. A novel empirical model decomposition and its primary application Geophysics Detecting and Application (in Chinese). Xi'an: Xi'an Map Press, 2007 : 201 -205. |
| [27] | 郭淑卿. EMD的频带滤波筛分方法. 中国民航大学学报 , 2008, 26(4): 20–34. Guo S Q. Improvement on EMD method of Hilbert-Huang transform. J ournal of Civil Aviation University of China (in Chinese) , 2008, 26(4): 20-34. |
| [28] | 高云超, 桑恩方, 许继友. 分离EMD中混叠模态的新方法. 哈尔滨工程大学学报 , 2008, 29(9): 468–451. Gao Y C, Sang E F, Xu J Y. A new method for separating mixed modes in empirical mode decomposition. J ournal of Harbin Engineering University (in Chinese) , 2008, 29(9): 468-451. |
| [29] | Park-McClellan, Parks T W, Burrus C S. Digital Filter Design. John Wiley & Sons , 1987: 54-83. |
| [30] | 刘代志, 钱昌松, 刘志刚等.基于EMD的联合模态单元滤波及其在高斯消噪中的应用[OL].中国科技论文在线, (http://www.paper.edu.cn).2008.7.22. Liu D Z, Qian C S, Liu Z G, et al. Joint mode cell filter based on EMD and its application on Gaussian denoising, [OL] (in Chinese). Chinese Science paper online (http://www.paper.edu.cn) 2008.7.22 |
| [31] | Flandrin P, Rilling G, Goncalves P. Empirical mode decomposition as a filter bank. IEEE Signal Processing Letters , 2004, 11(11): 112-114. |
 2010, Vol. 53
2010, Vol. 53


