地震波场模拟技术在认识地球内部结构和进行油气资源勘探研究领域具有重要的理论和实际意义.只有发展求解地震波传播方程的更有效、更精确的数值模拟方法,才能更好地指导理论研究和实际应用.求解波动方程的数值方法众多,目前比较流行的有:有限元方法[1~3]、有限差分法[4~8]、伪谱法[9, 10]、反射率法[11~13]和射线追踪法[14]等.这些方法各有优缺点,例如,有限元方法网格划分灵活,可方便地处理自然边界和不同的间断面,但其需要大的存储空间而且计算速度慢;有限差分法在粗网格条件下或在地球介质的强间断附近会产生伪波,引起严重的数值频散;谱方法则需要对波场作Fourier变换,因此计算量大,且难以处理人为边界,同时,当Courant(库朗)数较大时会产生严重的时间数值频散[15].
为有效压制数值频散,提高合成地震记录的质量,人们发展了众多高阶差分格式.目前研究最多且应用最广的高阶有限差分方法主要有两类:紧致方法[6, 16, 17]和交错网格方法[18~20].这两类方法的构造形式很多,但是这些方法在粗网格条件下或者在地下介质层间速度反差较大时数值频散仍然严重.为更好地压制数值频散,以提高计算效率,最近Yang等[21]发展了一种求解波传播方程的四阶龙格-库塔(RK)方法,有效地压制了数值频散,但当网格步长太粗时,仍有一些数值频散.为进一步改进这种RK方法在压制数值频散方面的能力,本文提出了一种基于四阶龙格-库塔方法[21]的改进算法.针对这种改进算法,我们研究了算法的稳定性和数值频散关系,并与四阶的Lax-Wendroff修正(LWC)方法[6]和位移-应力交错网格方法[22]进行了比较.数值频散分析表明,在粗网格条件下这种改进RK方法的数值频散误差远小于四阶LWC方法和交错网格方法.二维波场模拟结果表明,本文所提出的改进RK方法比四阶LWC方法和交错网格方法具有更高的计算效率和需要更少的存储空间,也比原RK方法具有更强的压制数值频散的效果.
2 基本的四阶龙格-库塔方法及其改进算法 2.1 求解常微分方程的四阶龙格-库塔方法考虑如下的常微分方程
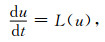
|
(1) |
其中u为待求函数,L(u)通常为已知的函数.则有如下求解常微分方程(1)的四级四阶Runge-Kutta(RK)格式[21, 23]:
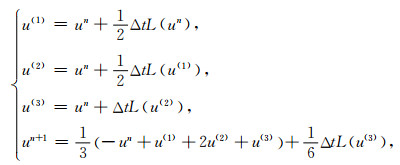
|
(2) |
其中,Δt为时间步长,un=u(nΔt),u(1),u(2),u(3)为中间变量.
由于式(2)为四级格式,用其计算时需要存储三个中间变量u(1),u(2)和u(3).为节省存储空间,我们将(2)式中的前两级和后两级分别合并,从而得到与之等价的二级计算公式:
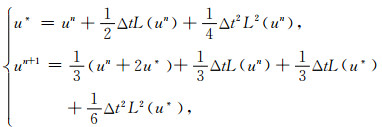
|
(3) |
其中,u*为中间变量,L2=L·L.
2.2 基本的龙格-库塔方法下面以二维声波方程为例来说明用公式(3)求解波动方程的具体实现.对于均匀介质情况,二维声波方程如下:
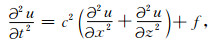
|
(4) |
其中u为位移,c为波速,f为力源函数,在下面的所有数值试验中,我们选取随时间变化的震源函数为
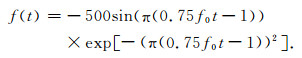
|
(5) |
为实现本文提出的改进RK方法,我们引入如下记号:
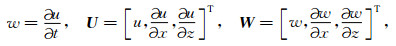
|
于是可将(4)式改写为如下形式:
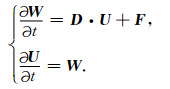
|
(6) |
其中,微分算子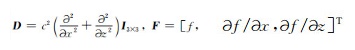

|
(7) |
其中,微分算子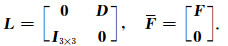
显然,方程(7)具有常微分方程组的形式,为此,我们考虑用求解常微分方程组的思想对其进行求解.可分为两步来实现:首先考虑其右端项的求解.事实上,右端项主要涉及到位移u和粒子速度w关于空间的二阶和三阶偏导数,对这些高阶偏导数的逼近我们可以采取局部插值近似方法,具体的计算公式可见附录A,这样方程(7)就转化成了一个半离散的常微分方程组;第二步就是求解这个半离散化的方程组(7),为此,本文采用四级四阶RK方法(3)进行时间导数的离散.具体计算公式如下:
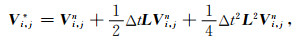
|
(8a) |
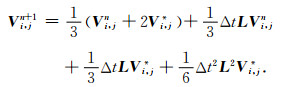
|
(8b) |
其中,Vn=V(nΔt),偏微分算子L2=L·L=Diag[D,D].
迭代算法(8)式显然是一个二级四阶格式,用其求解二维声波方程(4)时,只需要存储15个二维数组,而原四级四阶格式(2)则需要存储24个二维数组,因此采用算法(8)式求解波方程比直接用算法(2)式求解方程(4)可节省37.5%的存储空间,这有利于三维大尺度波场模拟和基于波动方程的逆时偏移.
2.3 四阶龙格-库塔方法的一种改进算法由于V*=[W*,U*]T,我们可将公式(8a)按向量V*的两个分量W*和U*写成如下等价形式:
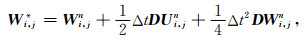
|
(9a) |
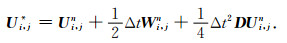
|
(9b) |
从计算公式(9a)和(9b)可以看出,在使用式(9b)来计算Ui, j*时,已通过式(9a)得到了Wi, j*,因此,从数学的角度来说,如将式(9b)中的Wi, jn用Wi, j*和Wi, jn的加权平均来代替的话,将会加速算法的收敛性.另一方面,我们以前的研究表明,尽管RK方法比其他的高阶方法有更好的压制数值频散的效果,但当网格步长很大时,RK方法仍有一些小的数值频散.因此,为进一步提高RK方法压制数值频散的能力,我们在算法式(9b)中引入非负加权参数η,从而获得了本文的改进RK方法如下
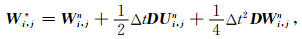
|
(10a) |
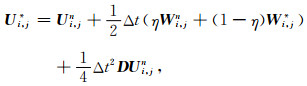
|
(10b) |
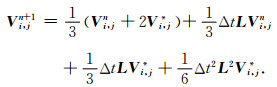
|
(10c) |
比较原RK方法(8)式和改进的RK方法(10)式,容易发现两种算法的差别仅在于将算法(8a)式计算分量Ui, j*时右端项中的Wi, jn(也就是(9b)中的Wi, jn)用一个加权平均项ηWi, jn+(1-η)Wi, j*来代替即可得新算法.这一加权思想在我们最近的研究中也曾使用过,并获得了好的结果[24].对于新引入的权值η,大量实验表明,一般可取0.5≤η≤1.另外,对比计算公式(8)和(10)可知,改进RK方法的计算量与原RK方法的计算量基本一样,也没有增加额外的存储量,但压制数值频散的能力却有很大改进,在后面的数值算例中将证明这一点.
3 稳定性条件在进行数值模拟时,为保证计算稳定,必须选择合适的计算参数.也就是说,在取定波速c和空间步长h后,时间步长Δt的选取必须满足一定的稳定性条件.为此,在这一节,我们用Fourier分析方法[15, 25]推导改进RK方法(10)式求解一维和二维声波方程时的稳定性条件.通过一系列的数学运算(见附录B),可以得到一维情况下的稳定性条件:
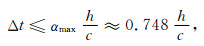
|
(11) |
其中,Courant数α定义为α=cΔt/h,而αmax为保证算法稳定的最大Courant数.
在二维均匀各向同性情况下,如果取空间步长Δx=Δz=h,那么采用与一维稳定性分析一样的方法可得到算法(10)式的稳定性条件:
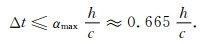
|
(12) |
需要指出的是,上述稳定性条件中最大Courant数αmax的近似值均是在权值η取0.7时得到的,在后面的所有数值计算中,我们也均取η=0.7.而当η取其他值时,应用附录B中的推导过程也很容易获得这一最大Courant数.另外,对于各向异性和非均匀介质中的弹性波传播情况,要直接获得改进RK方法的稳定性条件是很困难的,但我们可用局部均质化理论,并将(11)和(12)式中的波速c取为最大的P波速度,则(11)和(12)式也近似地成立.
4 频散分析差分方法是到目前为止最广泛使用的地震波场模拟方法.然而,由于有限差分方法利用有限的离散网格来近似逼近连续介质,这种离散就直接导致不同频率的地震波传播速度出现不同,也就是使相速度变为空间步长和时间步长的离散函数,从而出现数值频散,因此在合成记录时将看到主要震相之后出现“尾巴”,降低了合成图的分辨率.为此,本节我们将对这种改进RK方法的数值频散进行分析,并通过二维声波波场模拟进一步研究改进RK方法在压制数值频散方面的能力和计算效率.
研究离散化方法的数值频散就是要分析数值相速度偏离真实相速度的程度,换言之,分析数值频散误差.因此,在附录B中,我们利用Fourier分析方法首先给出了一维情况下的数值频散关系式(B10).下面我们利用关系式(B10)给出不同情况下的数值频散曲线.为了比较,我们同时也给出四阶LWC方法和交错网格方法(简称DSG)的数值频散关系曲线,其数值频散关系的理论结果可参见所引参考文献[22, 26],本文不再赘述.
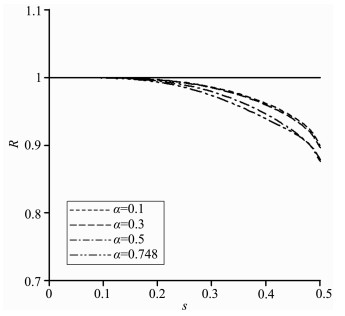
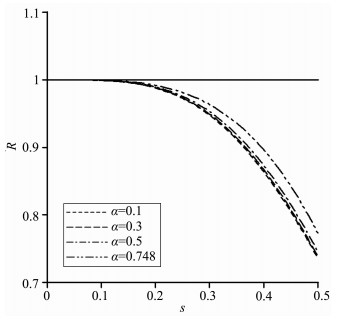
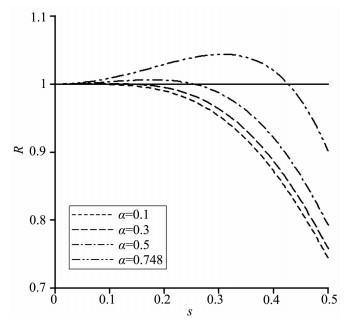
图 1~3分别给出了改进RK、LWC和DSG这三种方法在取不同Courant数时数值相速度与真实相速度之比R随空间采样率s变化的曲线图.从图 1可以看出,随着空间采样率s的增大,即随着空间步长的增大,改进RK方法的数值相速度逐渐偏离真实相速度,但4条频散曲线基本都位于R=0.89的上方,即改进RK方法的最大数值频散误差小于11%,而从四阶LWC方法和交错网格方法的频散曲线图 2和图 3可以看出其频散误差较大,图中表明,当α=0.1时,它们的最大频散误差均达到了约28%,这表明改进RK方法的频散误差明显小于四阶的LWC和交错网格方法.另外值得注意的是,随着Courant数α的增大,虽然改进RK方法的频散误差也增大,但从几条曲线的靠近程度可以知道Courant数的选取对改进RK方法的数值频散误差影响不大,这一特点也说明改进RK方法将在计算非均匀问题时具有优势.而图 3中的不同曲线则明显分开,这表明交错网格方法的数值频散误差对Courant数的选取具有很强的依赖性.
|
图 1 一维情况下改进RK方法在不同Courant数时的频散曲线图 Fig. 1 The dispersion curves of the improved RK method with different Courant numbers for the 1D case |
|
图 2 一维情况下LWC方法在不同Courant数时的频散曲线图 Fig. 2 The dispersion curves of the LWC method with different Courant numbers for the 1D case |
|
图 3 一维情况下交错网格方法在不同Courant数时的频散曲线图 Fig. 3 The dispersion curves of the staggered-grid method with different Courant numbers for the 1D case |
下面通过二维声波波场数值模拟计算,进一步研究改进RK方法的数值频散和计算效率.为此,考虑如下各向同性介质中的二维声波方程:
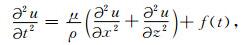
|
(13) |
其中,μ和ρ分别为弹性常数和介质密度.在这个数值实验中,我们选取μ=36.0GPa和ρ=2.0g/cm3,从而导致声波速度约为4243m/s,计算区域为0≤x≤24km,0≤z≤24km,选取网格步长为Δx=Δz=80m,网格数为301×301,时间步长为Δt=8.4×10-3s.震源位于计算区域的中心,其随时间变化的函数见公式(5),其中f0=15Hz.图 4(a~d)分别给出了用改进RK、原RK、LWC和交错网格等4种方法模拟的2.5s时刻的波场快照.对比这四幅图发现用这4种方法得到的地震波的“波前”是一致的,但是从图 4c和4d可以看出LWC和交错网格方法在此时有严重的数值频散和源噪声,而由改进RK方法得到的波场快照图 4a表现得非常清晰,没有可见的数值频散.比较图 4a和4b可以看出本文所给出的改进方法在压制数值频散方面确实优越于原RK方法.

|
图 4 二维均匀各向同性介质中的声波波场快照 (a),(b),(c),(d)为粗网格(Δx=Δz=80 m)条件下分别由改进RK,原RK,四阶LWC和交错网格四种方法得到的T=2.5 s时刻的波场瞬时快照,(e),(f)为细网格(Δx-Δz=20 m)条件下分别由四阶LWC和交错网格方法得到的T=2.5 s时刻的波场瞬时快照. Fig. 4 Snapshots of the acoustic wave-field at time T=2.5 s in the 2D homogeneous isotropic medium, generated by the improved RK method (a), the RK method (b), the LWC method (c), and the staggered-grid method (d) on the coarse grid (Δx=Δz=80 m), respectively. Snapshots at time T=2.5 s shown in Figures (e) and (f) are generated by the fourth-order LWC method and the staggered-grid method on the fine grid (Δx=Δz=20 m), respectively |
为了消除LWC和交错网格方法波场模拟时所产生的数值频散,必须缩小空间步长.对于这里所选取的震源频率和波速,经过大量的数值模拟,我们发现LWC和交错网格方法能够消除数值频散的最大网格步长可以取为Δx=Δz=20m,而网格数取为1201×1201,以保证计算区域一致.为比较,此时选取时间步长为Δt=2.1×10-3s以保证Courant数与粗网格条件下一致.图 4e和4f分别给出了细网格(Δx=Δz=20m)条件下用LWC和交错网格方法计算得到的2.5s时刻的波场快照.图 4e和4f表明,在细网格条件下LWC和交错网格方法均有效地消除了数值频散,得到清晰的计算结果.但是,此时的计算时间和空间存储代价却是非常大的.在计算耗时方面,得到图 4e和4f的CPU计算时间分别为583s和305s,而由改进RK方法得到图 4a的CPU时间仅为45s.这表明,在需要得到同样无可见数值频散波场的情况下,改进RK方法的计算速度分别是四阶LWC和交错网格方法的13倍和6.8倍.在空间存储方面,用改进RK方法得到图 4a需要15个二维数组存储相关的量,每个数组大小为301×301,而用LWC和DSG方法得到图 4e和4f则仅分别需要3个和5个二维数组,但每个数组大小为1201×1201.也就是说,改进RK方法需要的存储量仅约为LWC和交错网格方法的5/16和3/16.
在下面,我们给出几种方法计算的波形图,并与精确解比较.为此,我们选取声波方程(13)中的介质参数ρ=2.0g/cm3,μ=23.0GPa,计算区域为0≤x≤12km和0≤z≤12km;网格步长为Δx=Δz=40m,时间步长为Δt=1.0×10-3s,接收点位置为R(3.6km,6.0km),其他计算参数,震源函数和频率等与上一模型中的一样.
图 5a,5b和5c中虚线分别为用改进RK,LWC和交错网格这三种方法计算得到的R点处记录的波形,图中实线表示解析解,记录时间从0.4s到1.2s.对比这三幅图可以看出在粗网格条件下,用改进RK方法计算所得波形与精确解吻合得最好,计算误差最小,而四阶的LWC和交错网格方法不但在波峰处数值解与精确解相差较大,而且在主震相后面出现了明显的伪波动(数值频散),这一结果表明本文所提出的改进RK方法比高阶的LWC和交错网格方法在数值精度和压制数值频散方面均具有较大优势.

|
图 5 数值解与精确解的对比 (a),(b),(c)中虚线分别为改进RK,LWC和交错网格三种方法计算得到的单点波形记录,而图中实线均为精确解,记录时间从0.4s到1.2s. Fig. 5 Comparison of the numerical solutions and exact the analytic solution The dashed lines shown in (a), (b), and (c) are the numerical solutions, computed respectively by the improved RK method, the LWC method, and the staggered-grid method, and the solid lines are the analytic solutions. The record time is from 0.4 s to 1.2 s |
本节我们选取两个层状介质模型分别进行声波和弹性波波场模拟以进一步考察改进RK方法的计算效果.
5.1 三层模型在这个实验中,我们选取如图 6所示的三层介质模型进行声波波场模拟,声波在各层介质中的传播速度已显示于图中.震源为位于近地表(xs,zs)=(10km,0.04km)的Ricker子波,其随时间变化的函数仍取为公式(5)且f0=15Hz,空间网格步长和时间步长为Δx=Δz=20m和Δt=1.5× 10-3s,网格数为501×301.
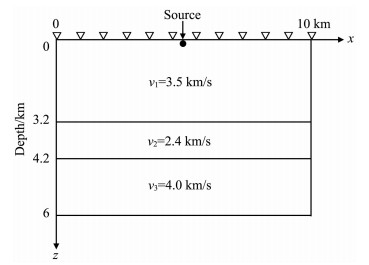
|
图 6 三层介质模型 Fig. 6 The model of three-layer media |
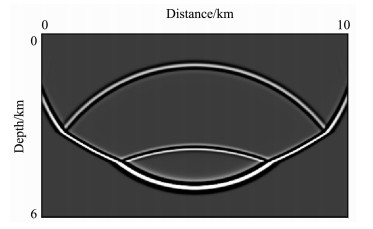
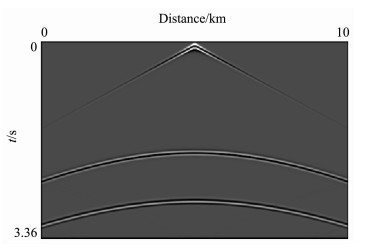
图 7为用改进RK方法模拟的1.6s时刻的波场瞬时快照.从图中可以看出经过两个内间断界面后的反射波和透射波的波前都非常清晰,而且在层间速度反差达到约1.7倍的情况下,在间断附近也没有可见的数值频散.图 8为用改进RK方法合成的地表地震记录,计算中我们使用了Yang等[27]提出的四次吸收边界条件来处理人工边界.地表地震记录图 8十分清晰,来自地层两个间断面的反射记录十分明显,这表明改进RK方法对于层间速度反差较大的地质模型具有较好的适应性.
|
图 7 对于三层模型,由改进RK方法计算得到的t=1.6s时刻的波场快照 Fig. 7 Snapshot of the acoustic wave field at time t=1.6 s, generated by the improved RK method for the three-layer model shown in Fig. 6 |
|
图 8 对于三层模型,由改进RK方法合成的地表地震记录 Fig. 8 The synthetic seismogram on the surface, generated by the improved RK method for the three-layer model shown in Fig. 6 |
为考察改进RK方法在模拟非均匀介质中地震传播的有效性,在最后的这个实验中,我们选取一个双层介质模型,其中上层为各向同性介质,下层为具有垂直对称轴的横向各向同性(VTI)介质.上层介质的弹性常数为λ=4.8,μ=6.5(GPa),介质密度为ρ1=3.2g/cm3;下层VTI介质弹性常数取为c11=40.8,c13=13.2,c33=50.6,c44=25,c66=13.8(GPa),介质密度为ρ2=4.2g/cm3.计算区域取为0≤x≤6km,0≤z≤6km,层间间断面位于z=3km处,震源函数与上面算例中所使用的一致,震源位置坐标为(x,z)=(3km,2.76km).空间网格步长和时间步长分别为Δx=Δz=20m和Δt=2.0×10-3s.
图 9(a~c)分别为用改进RK方法计算得到的位移三分量在0.96s时刻的波场快照.从图 9中可以很清楚地观察到多种波相.图 9b显示在上层介质中直达qSH波和经界面反射的qSH波为圆形,而下层介质中透射qSH波则为椭圆形.虽然图 9a和9c中存在多种波相,但是上层介质中直达的qP波和qSV波,经界面反射的qP波和qSV波以及转换波,下层介质中的透射qP波和qSV波等都可以很容易辨别,且从这些波场快照可观察到波前尖点和三叉区现象.

|
图 9 对于双层弹性介质模型(上层为各向同性介质,下层为VTI介质),由改进RK方法计算得到的t=0.96s时刻的位移三分量波场快照 Fig. 9 Snapshots of seismic wave fields at time t=0.96s for the three components of the displacement, generated by the improved RK method for the two-layer elastic medium model (The isotropic medium in the top layer and the VTI medium in the bottom layer) |
本文提出了一种改进的RK方法,它是原四阶龙格-库塔方法的一种改进算法.这种改进的RK方法在离散高阶时间导数时,由于将包含了四步计算的原RK方法合并为一种只包含两步的计算格式,从而在不降低精度的前提下减少了两个数组,进而使得改进RK方法在求解二维声波方程时的存储量减少了约37.5%.同时,该改进方法由于在第一步中引入了加权参数,使得这种改进RK方法比高阶的LWC方法、交错网格方法以及原RK方法具有更强的压制数值频散的能力.
数值频散分析表明,相对于四阶LWC和交错网格方法,改进RK方法具有更小的数值频散.例如,改进RK方法的最大频散误差仅约为11%,远小于LWC和交错网格方法的28%.而正是得益于改进RK方法具有弱数值频散的优良性质,使得我们可用较粗的网格和大的时间步长获得好的计算效果(可参见4、5节的数值算例),进而有效地提高了计算效率,节省了计算的CPU时间和存储量.这些良好特性,也使得这种改进的RK方法可能在研究大尺度复杂地层结构中的地震波传播、基于波动方程的地震偏移和地震层析成像等方面具有广泛的应用前景,这也将是我们后续工作中的研究内容.
附录 A 空间高阶偏导数的计算公式利用局部插值近似方法,我们可以得到位移和粒子速度关于空间的二阶和三阶导数的逼近公式.具体推导过程请参见文献[28]、[29],为方便起见,此处列出本文所使用的计算公式:

|
(A1) |

|
(A2) |

|
(A3) |

|
(A4) |

|
(A5) |

|
(A6) |

|
(A7) |
其中,δx2vi, jn=vi+1,jn-2vi, jn+vi-1, jn,Ex1vi, jn=vi+1, jn,Ex-1vi, jn=vi-1, jn,δz2和Ez的定义可类似给出.而向量v定义为v=(u,w)T,其中,u和w分别为位移和粒子速度.Δx和Δz分别为沿x和z轴方向的空间步长.而vi, jn,∂xvi, jn,∂zvi, jn,和∂mxkzvi, jn分别表示
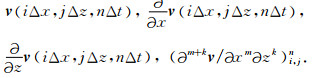
|
我们采用Fourier方法[15, 25]来推导改进RK方法的稳定性条件和频散关系.首先考虑一维情形,将谐波解

|
(B1) |
代入(10)式和(A1~A7)式中(k为波数),可得如下方程组

|
(B2) |
系数矩阵G的表达式如下

|
(B3) |
其中,
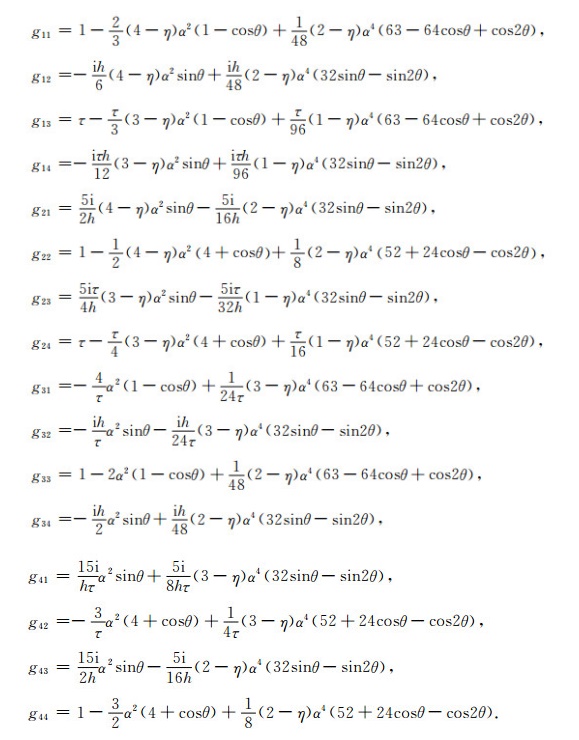
|
在上述表达式中,h=Δx为空间步长,τ=Δt为时间步长,i为虚数单位,α为Courant数,θ=kh,而η为改进RK方法中的加权参数.若取定权值η=0.7,则由数值求解特征值问题|λ(G)|≤1,我们可以得到如下稳定性条件:

|
(B4) |
或
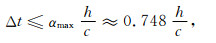
|
对于二维问题,我们仅考虑Δx=Δz=h的情形.若取定权值η=0.7,则完全与一维情况下的推导步骤相同,可以类似地得到如下稳定性条件:

|
(B5) |
或
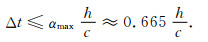
|
采用上述方法,我们也不难获得改进RK方法在取其他权值时的稳定性条件.
2 数值频散关系
下面推导改进RK方法在一维情形下的频散关系.记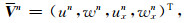

|
(B6) |
令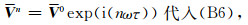

|
(B7) |
其中,ω为网格角频率.由于网格角频率与网格相速度cG和网格波长λG有如下关系

|
(B8) |
引入空间采样率s,并定义为

|
(B9) |
从而可以得到空间频散关系(网格相速度与真实相速度之比)的计算公式为

|
(B10) |
取定Courant数α,由线性方程组(B7)可解出ωτ(仅与s相关),代入式(B10)即可得到R关于s的表达式.
| [1] | Chen K H. Propagating numerical model of elastic wave in anisotropic in homogeneous media-finite element method. Symposiumof 54th SEG , 1984, 54: 631-632. |
| [2] | Seron F J, Sanz F J, Kindelan M, et al. Finite-element method for elastic wave propagation. Comm. Appl. Numerical Methods , 1990, 6(2): 359-368. |
| [3] | 杨顶辉. 双相各向异性介质中弹性波方程的有限元解法及波场模拟. 地球物理学报 , 2002, 45(4): 575–583. Yang D H. Finite element method of the elastic wave equation and waveiield simulation in two-phase anisotropic media. Chinese J. Geophys. (in Chinese) , 2002, 45(4): 575-583. |
| [4] | Alterman Z, Karal F C. Propagation of elastic waves in layered media by finite-difference methods. Bull. Seism. Soc. Am. , 1968, 58: 367-398. |
| [5] | Kelly K, Ward R, Treitel S, et al. Synthetic seismograms: a finite-difference approach. Geophysics , 1976, 41: 2-27. DOI:10.1190/1.1440605 |
| [6] | Dablain M A. The application of high-order differencing to the scalar wave equation. Geophysics , 1986, 51: 54-66. DOI:10.1190/1.1442040 |
| [7] | Virieux J. P-SV wave propagation in heterogeneous media: velocity-stress finite-difference method. Geophysics , 1986, 41: 889-901. |
| [8] | 董良国, 马在田, 曹景忠, 等. 一阶弹性波方程交错网格高阶差分解法. 地球物理学报 , 2000, 43(3): 411–419. Dong L G, Ma Z T, Gao J Z, et al. A staggered-grid high-order difference method of one-order elastic wave equation. Chiness J. Geophys. (in Chinese) , 2000, 43(3): 411-419. |
| [9] | Kosloff D, Baysal E. Forward modeling by a Fourier method. Geophysics , 1982, 47: 1402-1412. DOI:10.1190/1.1441288 |
| [10] | Huang B S. A program for two-dimensional seismic wave propagation by the pseudo-spectrum method. Comput. Geosci. , 1992, 18: 289-307. DOI:10.1016/0098-3004(92)90082-3 |
| [11] | Booth D C, Crampin S. The anisotropic reflectivity technique: anomalous arrives from an anisotropic upper mantle. Geophys. J. R. Astr. Soc. , 1983, 72: 767-782. DOI:10.1111/j.1365-246X.1983.tb02832.x |
| [12] | Chen X F. A Systematic and efficient method of computing normal modes for multi-layered half-space. Geophys. J. Int. , 1993, 115: 391-409. DOI:10.1111/gji.1993.115.issue-2 |
| [13] | Zhang H M, Chen X F, Chang S H. An efficient numerical method for computing synthetic seismograms for a layered half-space with sources and receivers at close or same depths. PureAppl. Geophys. , 1993, 160(3/4): 467-486. |
| [14] | Chapman C H, Shearer P M. Ray tracing in azimuthally anisotropic media-II: quasi-shear-wave coupling. Geophys. J. , 1989, 96: 65-83. DOI:10.1111/gji.1989.96.issue-1 |
| [15] | Yang D H, Peng J M, Lu M, et al. Optimal nearly analytic discrete approximation to the scalar wave equation. Bull. Seism. Soc. Am. , 2006, 96: 1114-1130. DOI:10.1785/0120050080 |
| [16] | Igel J, Weber M. SH-wave propagation in the whole mantle using high-order finite differences. Geophys. Res. Lett. , 1995, 22: 731-734. DOI:10.1029/95GL00312 |
| [17] | 王书强, 杨顶辉, 杨宽德. 弹性波方程的紧致差分方法. 清华大学学报(自然科学版) , 2002, 42(8): 1128–1131. Wang S Q, Yang D H, Yang K D. Compact finite difference scheme for elastic equations. J. Tsinghua Univ. (Sci. & Tech.) (in Chinese) , 2002, 42(8): 1128-1131. |
| [18] | Levander A R. Fourth-order finite-difference P-SV seismograms. Geophysics , 1988, 53: 1425-1436. DOI:10.1190/1.1442422 |
| [19] | Graves R W. Simulating seismic wave propagation in 3D elastic media using staggered-grid finite differences. Bull. Seism. Soc. Am. , 1996, 86: 1091-1106. |
| [20] | Moczo P, Kristek J, Vavrycuk V, et al. 3D heterogeneous staggered-grid finite-difference modeling of seismic motion with volume harmonic and arithmetic averaging of elastic moduli and densities. Bull. Seism. Soc. Am. , 2002, 92: 3042-3066. DOI:10.1785/0120010167 |
| [21] | Yang D H, Chen S, Li J Z. A Runge-Kutta method using high-order interpolation approximation for solving 2D acoustic and elastic wave equations. Journal of Seismic Exploration , 2007, 16: 331-353. |
| [22] | Moczo P, Kristek J, Halada L. 3D fourth-order staggeredgrid finite-difference schemes: stability and grid dispersion. Bull. Seism. Soc. Am. , 2000, 90(3): 587-603. DOI:10.1785/0119990119 |
| [23] | Jiang G S, Shu C W. Efficient implementation of Weighted ENO schemes. J. Comput. Phys. , 1996, 126: 202-228. DOI:10.1006/jcph.1996.0130 |
| [24] | 王磊, 杨顶辉, 邓小英. 非均匀介质中地震波应力场的WNAD方法及其数值模拟. 地球物理学报 , 2009, 52(6): 1526–1535. Wang L, Yang D H, Deng X Y. A WNAD method for seismic stress-field modeling in heterogeneous media. Chinese J. Geophys. (in Chinese) , 2009, 52(6): 1526-1535. |
| [25] | Richetmyer R D, Morton K W. Difference Methods for Initial Value Problems. New York: Interscience, 2002 . |
| [26] | Sei A, Symes W. Dispersion analysis of numerical wave propagation and its computational consequences. J. Sci. Comput. , 1994, 10: 1-27. |
| [27] | Yang D H, Wang S Q, Zhang Z J, et al. N-times absorbing boundary conditions for compact finite-difference modeling of acoustic and elastic wave propagation in the 2D TI medium. Bull. Seism. Soc. Am. , 2003, 93: 2389-2401. DOI:10.1785/0120020224 |
| [28] | Yang D H, Teng J W, Zhang Z J, et al. A nearly-analytic discrete method for acoustic and elastic wave equations in anisotropic media. Bull. Seism. Soc. Am. , 2003, 93(2): 882-890. DOI:10.1785/0120020125 |
| [29] | Yang D H, SongG J, ChenS, et al. An improved nearly analytical discrete method: An efficient tool to simulate the seismic response of 2-D porous structures. Journal of Geophysics and Engineering , 2007, 4(1): 40-52. DOI:10.1088/1742-2132/4/1/006 |
 2010, Vol. 53
2010, Vol. 53


