2. 中国地震局地震预测研究所, 北京 100036
2. Institute of Earthquake Science, China Earthquake Administration, Beijing 100036, China
GPS[1, 2]等空间大地测量技术的发展,在大、中空间尺度上把观测精度从传统测量技术难以超过的10-6提高到了10-8~10-9水平,给出了基于全球统一参考框架(ITRF)的地壳运动观测信息,使大区域以致全球的地壳运动监测能力有了根本性提升.我国自20世纪80年代末开始建立和发展GPS观测网[3],到1998年由国家重大科学工程建设“中国地壳运动观测网络”[4~6],GPS观测网络有了很大发展,初步形成了对我国大陆内部较大构造块体整体运动与变形的观测能力和对华北、川滇及青藏块体东北缘等多震区的较高空间分辨力的观测能力.随着GPS观测资料日益丰富,利用GPS资料开展地壳运动及动力学等方面的研究已在地学研究领域中占有很大比重,在各有关刊物中报道了大量研究结果.在大量研究结果中,不同研究者给出的GPS地壳运动与变形图像丰富多彩,包括相同来源的GPS资料所给出的地壳运动与变形图像也可能有所不同,如中国大陆水平应变场结果的不一致问题[7].怎样把实际资料反映的不同空间、时间尺度的地壳运动与变形信息客观恰当地表达出来,是值得探究的问题.从GPS能够直接获取的地壳运动信息来看,由GPS速度场可给出最直观的地壳运动差异图像,应变场能够全面表达变形的性质与强度.但速度场是与参考基准相联系的,不同研究者往往根据研究问题的需要给出相对于不同参考基准的速度场图像.应变场虽然与基准无关,但解算应变场的方法也有多种,使得不同研究者给出的应变场图像也有所不同.本文论述了应用经典的大地测量数据处理理论之一的最小二乘配置原理,建立地壳运动模型和应变场的方法,讨论了基于严密的大地测量数据处理模型建立不同约束和不同运动学与几何变形含义的地壳运动速度场和反映不同空间尺度,顾及不同空间频域的应变场的问题,探讨了利用GPS观测结果客观给出最恰当的水平相对运动速度场和应变场图像的问题,并结合中国地壳运动观测网络区域网复测资料,分别以中国大陆区域整体及首都圈地区不同空间尺度的区域作为研究区进行了实际应用的讨论.
2 地壳运动速度场统一模型及其讨论 2.1 最小二乘配置地壳运动速度场统一模型 2.1.1 应用最小二乘配置原理建立速度场统一模型虽然利用GPS等空间对地观测技术建立了非常重要的全球ITRF(International Terrestrial Reference Frame)参考架,使我们可以获得GPS站点在全球统一参考架下的位置随时间的变化.但在实际研究中因涉及不同尺度的空间区域和研究不同的问题,还需要根据实际研究的需要选取不同的参考基准.不同的参考基准都有其明确的含义,并要符合描述相对运动及几何变形约束的严密性.最小二乘配置法具有理论上的严密性,可综合估计非随机参数、具有随机属性的信号和随机误差,其用于重力场空间分布模型的建立有成功范例[8].把它用于GPS观测地壳运动速度场模型的建立,是自然的选择.根据最小二乘配置原理[8, 9],其综合模型为
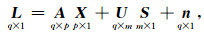
|
(1) |
其中L为观测向量,X为非随机参数向量,A为系数阵,反映X对L的贡献,S为信号向量,它既包含研究时空域内已观测点的信号,也包含未观测点的信号,U是一个长方矩阵(m≥q),由左部q阶(与已测点对应)单位矩阵和右部(m-q)阶的零矩阵(与未测点信号对应)组成,n为观测误差噪声.这个模型的含义是,观测值L中包含固有参数确定的变化部分、偏离这种固有变化的信号部分,以及观测的误差噪声这三个部分.根据最小二乘原理,可求得(1)式模型中非随机参数X和信号S的解及相应精度估计.由于S可在研究区任意位置取点而给出最优推估值,这样就给出了研究区信号的连续分布模型.应用最小二乘配置原理,可以把基于不同约束的参考基准的地壳运动的描述统一于以下的运动模型之中,建立GPS统一速度场模型,根据表达习惯,我们将模型(1)式改写,即

|
(2) |
式中Vo为GPS站水平运动观测速度(或位移)向量,通常为全球参考框架的GPS站速度或位移;Ω为欧拉刚性运动模型参数向量,由于GPS观测区域可能很大,我们需要在球面内讨论问题;A是其系数矩阵(是GPS观测站坐标信息),这样由AΩ表示GPS观测速度Vo中包含的刚性运动部分;Vs表示从观测速度Vo中扣除某种刚性运动后剩余部分中的有效信号部分(经过噪声滤波后的)剩余速度,Vs是空间域连续分布的.按最小二乘配置模型,(2)式中非随机参数Ω和信号Vs的解
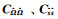
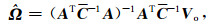
|
(3) |
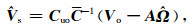
|
(4) |
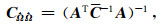
|
(5) |
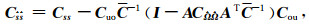
|
(6) |
其中,
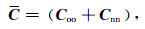
|
(7) |
Coo是研究区GPS站点速度观测向量Vo的协方差,描述研究区GPS站速度群体空间分布相关性与离散性.Cnn是Vo观测误差自协方差,描述各单个GPS站点观测速度自身的离散性(反映观测精度)及其不同站间误差相关性.Cuo是推估(点)信号与已测(点)观测信号的协方差矩阵.由(2)式模型不仅由Vs给出扣除研究区整体刚性运动后的连续分布的速度场,也给出了基于GPS观测建立的多种速度场的关系:Vo表示基于全球参考框架的GPS站实测速度场,Vo -AΩ表示扣除某种刚性运动后的GPS站实测速度场.
2.1.2 实现模型解算的条件及模型严密性第一,在对(2)式模型求解过程中用到3个协方差阵,只有Cnn已知,由GPS速度场解算结果给出,而Coo、Cuo是未知的,需利用实际资料进行构建.基于地壳连续变形的假设,在空间上很靠近的两个站点的速度值必然相关性高,而若两个相距较远的站点速度值的相关性必然较低.高斯型函数
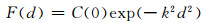
|
(8) |
(式中d为观测点间距离,C(0)表示d=0为方差)能够较好地表达不同点间观测信号的协方差F(d)随着点间距离d的增大而衰减的关系.研究表明,地壳运动与变形观测信号的协方差分布与高斯型协方差函数模型是相一致的,由此可以根据GPS速度场的数据建立经验型的协方差函数,从而构建协方差阵Coo、Cuo.
第二,按最小二乘配置理论模型(上述(1)式),信号S与噪声n都是归中的,即E(S)=0,E(n)=0.而(2)式模型是讨论球面内的地壳运动问题,Vs是扣除欧拉刚性运动模型AΩ理论速度后的剩余部分的信号,AΩ的理论速度在球面不同空间位置有大小、方向变化,因而Vs的0值是对应AΩ的,而不同于平面坐标系中通常以S总平均值作为E(S)的统计量.从研究地壳相对运动与变形的实际含义来看,如果研究区的水平运动完全符合欧拉刚体运动模型确定的理论值,这时(2)式中Vs=0,表明GPS只观测到噪声,研究区没有地壳相对运动与变形的信号.若Vs≠0,表明研究区有相对运动与变形,信号Vs在具体空间点上的速度的大小及方向体现了具体点位地壳运动速度偏离刚体运动AΩ的地壳变形信息的强弱及性质.所以相对运动与变形0值不是Vo的平均值,而是AΩ确定的刚体运动速度值,这样保持了最小二乘配置模型实际应用的严密性.
第三,最小二乘配置统一速度场模型建立的相对运动速度场具有参考基准的严密性.许多研究者利用全球ITRF参考框架的GPS速度场直接解算出某个块体的欧拉参数,用来扣除刚体运动而得到了相对某个块体的相对运动速度场,或者扣除研究区的整体刚性运动,都可以比较简单地用最小二乘求解获得[10].由于GPS站点的空间分布通常是不均匀的,造成直接用各GPS站速度解算时不同空间位置的权重不同,观测点密集的地点权重大,会导致相对运动速度场的基准不严密.且不同期复测资料可能出现GPS点分布的变化,难以保持参考基准的相对稳定性.由本文(2)式模型建立的相对运动速度场在进行欧拉模型参数解算时,采用速度信号Vs足够密度的网格值进行解算约束,由于网格值是根据GPS站观测速度获得的最优推估结果,因而较好地解决了GPS站点空间点分布不均匀导致不同地点权重不一的问题,也可使不同期速度场的参考基准更趋一致.
2.2 中国大陆地壳运动整体无旋转基准速度场 2.2.1 速度场协方差矩阵的构建图 1给出了中国地壳运动观测网络正式公布的1999~2001年GPS速度场(中国大陆境内全部929个站)实测的(Vo-AΩ)作为信号计算的协方差与高斯型函数拟合结果.这里是直接由GPS站实测速度计算一定距离范围的全部GPS站各两站之间的协方差,并以E向协方差与N向协方差取平均值建立构建统一的协方差模型(不涉及GPS前期精密解算的误差方差-协方差阵).因本文仅用中国地壳运动观测网的数据,在按站间距离分档计算中近距离的站点数量偏少,噪声较大,尤其青藏地区较大范围站点分布不足,使协方差分布在近距离的区间吻合程度降低,但总体上仍与函数模型相一致.由图 1给出的高斯型函数模型参数K=0.00166,用于构建速度场协方差矩阵Coo及Cuo.
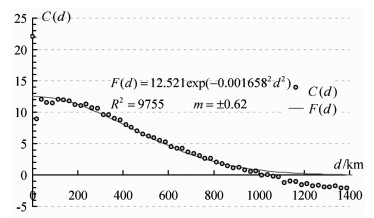
|
图 1 中国大陆GPS站水平运动速度协方差-距离分布(1999~2001) Fig. 1 Covariance-distance distribution of the horizontal movement velocities of GPS stations (1999~2001) |
中国大陆地壳运动整体无旋转基准速度场实际上就是扣除中国大陆整体刚性运动的结果,已有文献讨论[11, 12].下面采用本文最小二乘配置速度场统一模型(2)式,通过严密解算给出经滤波的中国大陆整体无旋转基准的连续分布速度场,即(2)式模型中Vs,分布图像如图 2,以及中国大陆整体无旋转基准的实测速度场,即(2)式模型中(Vo-AΩ),如图 3.图中GPS站点速度空间分布显示少数GPS站点误差较大,也有空间趋势明显不协调的站,从方法研究的角度本文采用了全部GPS站数据.

|
图 2 经误差噪声滤波的中国大陆水平运动速度场(经误差噪声滤波) Fig. 2 The horizontal movement velocity field (after the error noise filter) in China continent |
|
图 3 中国大陆水平运动实测速度场图 Fig. 3 The horizontal movement velocity field (observation) |
图 2中用(2)式模型Vs速度误差椭圆长半径给出了误差的空间分布,速度场误差分布主要与GPS站点的密度及速度场解数据中给出的误差有关.经滤波的连续分布速度Vs场的网格点平均精度[13]中误差为±1.01mm/a,高于根据前期GPS速度场解给出误差计算的平均中误差±1.7mm/a.GPS站密度最大的北京及其附近地区和GPS站分布密度较大且处于中国大陆中心的兰州一带(由于周围大范围的GPS站速度都对这个区都有不同程度贡献)误差最小(在±0.1~±0.2mm/a之间),GPS站点较少的东北地区(参见图 3)东北边境突出点由于对推估值有贡献的站点太少,其误差最大(±3.5mm/a).大陆内部在青藏交界地区较大范围没有GPS站,其速度场误差也较大(±1.8 mm/a).这一结果表明,最小二乘配置模型给出的连续分布速度场误差估计虽然是基于模型的结果(属于内精度),但具有相对精度高低的客观性.
2.2.3 整体无旋转基准速度场所反映的地壳相对运动与变形含义目前在有关文献中利用GPS资料给出了三种具有不同含义的速度场:全球ITRF参考框架的速度场[14, 15],相对于欧亚大陆的速度场[14, 16, 17]和反映中国大陆内部相对运动的整体无旋转基准速度场(图 2、图 3).三种速度场都可以赋予构造运动和大陆动力学方面的解释.而从运动学和几何变形的直接含义是:全球参考框架的中国大陆速度场包含有欧亚板块相对于全球参考框架的刚性运动、中国大陆相对欧亚板块的整体刚性运动及中国大陆内部的相对运动,是三者的叠加.相对于欧亚大陆的速度场是中国大陆整体相对欧亚板块刚性运动与中国大陆自身内部相对运动的叠加.中国大陆无整体旋转基准速度场则是完全扣除了整个中国大陆刚性运动后的剩余速度分布,它是对整个中国大陆发生变形状态的直观显示.也就是说,如果中国大陆没有发生变形,则这种模型的速度场将变成“零速度”场,而看不到任何点的速度矢量分布.从图 2、图 3可看到,喜马拉雅构造带靠近板块边界处地壳运动北北东向速度最大,表明其受到印度板块推挤引起的相对运动变形速度最快.而川滇菱形地块向南的速度最大,表明其被挤出引起的相对运动与变形最显著.中国大陆东部地壳运动也显示有分区差异,东北地区以NWW运动为主,华北地区是转折过渡区,而华南地区整体呈现ES向运动趋势,这种相对运动分区特征可以从基于层析成像等技术给出的大区域深部结构图像解译的太平洋板块向西俯冲对中国大陆东部影响的研究成果中[18]得到很好的解释.
2.3 最小二乘配置速度场统一模型不同速度场及其应用 2.3.1 相对不同含义参考基准的相对运动速度场对于(2)式的地壳运动模型,当求取模型参数Ω的约束条件不同,相应就有不同含义的Vs速度场.把Ω设定为不同区的整体刚性运动参数,可获得相对一个板块或块体的地壳运动速度场,也可以获得某个研究区的相对运动速度场.模型参数Ω还可作其他定义,如当研究某块体边界带活动断裂带的相对运动与变形时,可以利用断裂带两侧附近等宽度区域的相对运动平衡作为约束来解算出Ω参数,从而使断裂带的相对运动能够清晰地显示出来[19].
2.3.2 连续分布速度场及误差噪声滤波按最小二乘配置模型,对已测点速度的滤波起作用的是加入到(4)式珚C中的误差自协方差Cnn(由前期GPS速度解中给出).在没有获得速度场解的方差-协方差数据时,也可采用速度场总方差的某个百分比构建Cnn加入协方差主对角元素,这属于等权的滤波处理,这时滤波的强度是可人为调定的.但加滤波信号是必要的,否则当存在一些观测点密集分布区时可能导致解算失败(由于不加滤波信号时连续模型值必然与实际观测值重合,这只能是观测点分布都有一定跨度的情况下才能做到).
连续速度(Vs)场分布的平缓程度主要取决于解算中用到的经验协方差函数模型((8)式)的参数K.对于同类观测数据,若研究区域较大时速度场协方差统计相关范围也较大,这样获得的经验协方差函数模型的K值就较小,使得速度场分布相对平缓.若研究区域较小其速度场协方差相关范围也较小,连续分布速度场就能反映较高频域细节的变化,实际是顾及一定频域相对运动差异的速度场.
2.3.3 不同基准速度场实际包含的地壳变形信息的一致性以上的论述表明,虽然地壳运动相对量(如两个站之间的距离)是确定性的,但由于选取的参考基准不同使得地壳运动的图像是多样的.不过,由于基准参数不包含地壳相对运动与变形信息,基准转换过程保持了地壳相对运动的不变性,在球面内讨论具体就是两个GPS站间弧长的变化量保持不变.这又表明尽管同一地区相同资料来源给出的不同基准的速度场显示出不同的图像,但就其中实际包含的地壳变形信息是完全一致的.
2.3.4 相对运动速度场适用范围和参考基准误差问题本文给出的模型是在已经获得全球参考框架速度场基础上建立相对运动速度场的统一模型.实质是选定一个区域(或块体)解算提取欧拉刚性运动参数,而获得扣除这一刚性运动成分后的速度场.这里主要是为了使相对运动的描述更为直观.因而适用于区域内部相对运动的描述或者相邻块体之间的运动描述.但更大区域如研究整个欧亚板块内部的相对运动自然应选择欧亚板块的基准,研究全球的板块运动自然要用全球参考框架.
关于基准转换可能造成误差的问题,由于基准转换过程中没有损失任何变形信息,当关注的是地壳相对运动变形的空间分布,而不是运动量值大小时,可以不考虑基准转换的误差.这与自由网平差与变形分析中认为坐标参数的误差无基准误差的影响[13]是一致的.若考虑基准转换的误差影响,则可通过估计基准转换参数误差而给出基准转换引起的GPS站速度的误差.当观测速度与刚体运动模型值接近(如以华南地块为基准[20])或者解算基准参数所用的观测点多时基准参数估值的误差都很小.如直接用中国大陆近千个GPS站解欧拉矢量(基准转换参数)的误差在10-10量级上(三分向中误差为0.39、±1.1、±0.83(×10-10)),按误差传播GPS站速度的基准转换改正数的中误差为在±0.16~±0.40mm/a(平均精度为±0.19 mm/a),以在ITRF框架的站速度中误差±1.30 mm/a为例估算,顾及基准误差影响后GPS站速度中误差增加量仅为±0.01~±0.06(mm/a),属可忽略的量级.
3 应用最小二乘配置建立顾及不同频域的应变场 3.1 应变尺度相对性与连续分布应变场从一般概念讲,由于应变量是由观测点之间的相对运动来决定的,它不依赖于参考基准.应变量的大小和张或压、左旋或右旋剪切等不受位移或速度场的基准影响.但实际上不同的研究者基于相同的速度场数据给出的应变场图像也往往不完全一致.石耀霖等[7]注意到了不同研究者给出中国大陆应变场的不一致性,研究讨论了多种应变计算方法.江在森等[21]曾根据实际资料研究提出了地形变资料求解应变值的尺度相对性问题,给出了应变计算值的统计平均值和均方差存在随着计算图形尺度增大而呈幂函数衰减的统计特征.从根源上来认识,以地面点为观测对象的大地测量技术只能以很高的精度来测定两个点的相对位移或者一个点相对参考基准的位移,由于观测点分布密度的局限和地壳介质的不均一性,不能精确测定一个点的应变,应变计算值只能是相对测点跨度范围、基于均匀变形假设或某种假设的应变近似值.因此,如果采用邻近点组成三角形单元的计算方法,由于观测误差噪声影响和可能的断层活动类变形在小尺度图形单元计算中显著放大,高应变值通常是在观测点密度较高的区域出现,而观测点分布稀疏的地区应变值通常较低.对中国大陆GPS区域网资料采用相邻点组成三角单元的计算获得的应变量值的范围跨10-6/a~10-10/a这样大的量级范围,表明这样的结果在进行较大区域应变场计算中由于观测点分布密度、观测误差等影响,使得应变值空间分布并不具有可比性,降低了应变场空间分布的可参考性.另外,要制作应变参数空间分布图像,需要单元应变计算结果做粗差剔除和网格化处理,实际上属于不严谨的连续化处理与滤波过程.因而建立经滤波的连续分布应变场是必要的.随着GPS观测资料不断给出较大空间覆盖范围具有一定密度的地壳水平运动速度场结果,许多研究者采用了在建立连续分布速度场模型基础上进行应变场计算的方法,其中具有代表性的多面函数拟合法[15, 22~24]、球谐函数展开法[7]和最小二乘配置法[8, 9, 25~27]等,都能够较客观地反映观测资料的实际,但进一步的研究表明,在抗差性和给出精度评定方面最小二乘配置法具有优势.
3.2 应用最小二乘配置建立顾及不同频域的应变场采用带误差噪声滤波的最小二乘配置模型,利用连续分布速度场模型通过应变率与位移速度的偏导关系,
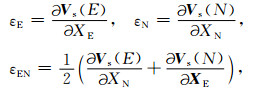
|
(9) |
(式中Vs(E)、Vs(N)、XE、XN分别为东向、北向速度信号和坐标的分量,εE、εN、εEN为应变张量的元素)可进行连续分布应变场的整体解算,在有关文献[25~27]中已经给出在高斯投影平面和在球面的具体解算方法,这里不作具体展开论述.2.3节已讨论了最小二乘配置给出经噪声滤波的连续分布速度场Vs实际是顾及一定频域的速度场,基于此速度场模型解算的应变场就是相对一定空间频域范围地壳变形的应变场.
3.3 不同频域应变场及其有效变形信号显著性分析应用讨论 3.3.1 顾及不同频域的应变场图像上已述及,采用实测速度场数据提取经验协方差分布模型时,协方差随站点间距的衰减模型不仅与速度数据空间分布有关,还与研究区域大小有关.由取得不同协方差衰减模型构建的协方差阵解算出的顾及不同变形频域的应变场在图像上的差异也比较明显.如以中国大陆作为研究区高斯型协方差函数模型参数K=0.0016,相关性衰减到1%的范围约1300km.若以南北地震带中南部地区为研究区,其K=0.0033,协方差相关范围约为中国大陆的一半.顾及不同频域的应变场图像侧重于反映不同频域的变形信息.文献[27]、[20]利用中国地壳运动观测网络工程的速度场数据分别给出的中国大陆与川滇地区面应变等值线图在川滇地区图像分布上就有细节上的差异,川滇地区面应变图中有的局部变化在中国大陆面应变图[27]中就看不到,这就是由于中国大陆应变图只顾及到相对低频域的地壳变形,某些局部小尺度的变化被当作噪声滤波去掉了而无法显示.这表明,由于在应变场连续分布的解算中要进行误差噪声滤波处理,因而,不受参考基准影响的应变场的惟一性是相对的,其必然受到具体解算时顾及空间不同频域和误差滤波的影响.
3.3.2 有效变形信号显著性分析基于对连续分布场的基本认识,如果这个场存在,在空间位置很靠近的测点的观测值自然很接近,观测点之间观测信号的相关性自然随点距的增大而衰减.如果不具备这样的统计特征,则表明观测数据中的信噪比太低使得难以识别出有效的变形信号.
对于更小的研究区进行应变场的计算,主要是提取相对高频域变形信息.由于相对高频域的变形信息更可能与噪声混杂在一起而难以区分,采用最小二乘配置方法,通过对实测速度场数据提取经验协方差函数参数的统计分析,有助于了解研究区是否观测到相对于观测精度的有效变形信号.如以首都圈为研究区,GPS观测速度场的信噪比相对较低,对1999~2001年、2001~2004年及1999~2004年3时段速度场数据进行经验协方差函数提取时,仅有1999~2004年速度场由于累积变形较显著而能够提取经验协方差函数,其K=0.0093,实测速度场的协方差的统计分布与高斯型函数相关系数R2=0.71,协方差相关性衰减到1%的范围仅为232.1km.表明速度场观测数据中包含有可识别的有效变形信息.而1999~2001年速度场的协方差的统计分布与高斯型函数不相关,2001~2004年速度场协方差的统计分布与高斯型函数相关系数R2=0.29,K=0.0101,也表明其变形信息不显著.虽然通过人为设定经验协方差函数模型参数也可以做出1999~2001年、2001~2004年应变场解算结果,但这样给出的应变场实际所包含的有效变形信息是不足的.由1999~2004年速度场数据解算出的最大剪应变分布图可显示出文安、任丘东南侧一个明显的局部高应变区(图 4),虽然是局部小区GPS点间相对运动造成的,在中国大陆大区域的处理中把它当作噪声被滤波去掉了,但这个局部小区变形是属于GPS观测可识别的.
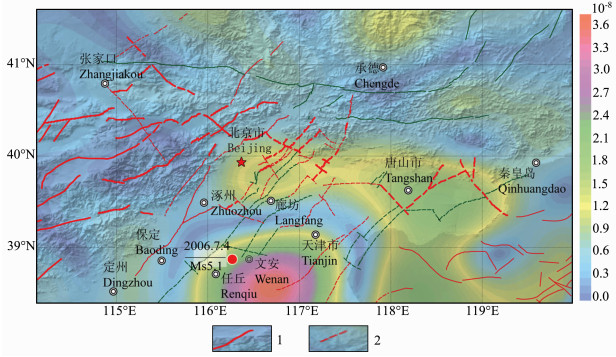
|
图 4 首都圈地区最大剪应变率分布图(1999~2004) 1.活动断裂,2.隐伏断裂. Fig. 4 Spatial distribution of maximum shear strain rate in metropolitan region (1999~2004) 1.Active fault, 2.Concealed fault. |
(1)应用最小二乘配置原理建立的水平运动速度场统一模型,根据观测数据空间分布通过经验协方差函数构建速度场信号协方差阵,可给出相对于不同参考基准(如相对一个板块、地块、研究区或断裂带)的经误差噪声滤波后的连续分布速度场,并可给出包含误差噪声的GPS站实测速度场.各种具有不同含义的地壳水平运动速度场所包含的地壳相对运动与变形的信息是一致的,只是从直观图像上的表现效果有不同.区域整体无旋转速度场由于扣除了研究区域中不包含变形的刚体运动成分,从而使相对运动与变形信息更突出.采用最小二乘配置建立的速度场统一模型可较好地解决由于GPS站空间分布不均匀对扣除刚性运动模型参数解算带来的影响问题,而获得相对某个块体或区域的有较严密的相对运动含义的速度场.
(2)由于观测点分布密度的局限和地壳介质的不均一性,由大地测量资料难以获得精确的应变场.由于测量误差的存在,进行连续分布应变场的解算中需做误差噪声滤波处理.因而,不受参考基准影响的应变场的惟一性是相对的,其必然受到具体解算时顾及空间不同频域和误差滤波的影响.应用最小二乘配置模型建立的连续应变场进行误差噪声滤波具有一定的客观性,可根据实际研究区大小,较合理地获得顾及空间不同频域相对运动与变形的应变场,且用于小区域相对高频域的应变场解算时,可给出有效变形信号显著性分析.
致谢本文所用的GPS速度场数据来源于中国地壳运动观测网络数据中心,并感谢中国地震局地质研究所王敏研究员提供的帮助.感谢审稿专家提出了建设性的修改意见.
| [1] | Dixon T H. An introduction to the Global Positioning System and some geological application. Reviews of Geophys , 1991, 29: 249-276. DOI:10.1029/91RG00152 |
| [2] | Larson K M, Freymuell E R J T, Phil Ipse N S. Global plate velocities from the Global Positioning System. J. Geophys. Res. , 1997, 102: 9961-9981. DOI:10.1029/97JB00514 |
| [3] | 王琪, 赖锡安, 游新兆, 等. 红河断裂的GPS监测与现代构造应力场. 地壳形变与地震 , 1998, 18(2): 49–56. Wang Q, Lai X A, You XZ, et al. GPS measurement and present tectonic stress field in the Honghe fault. Crustal Deformation and Earthquake (in Chinese) , 1998, 18(2): 49-56. |
| [4] | 马宗晋, 陈鑫连, 叶叔华, 等. 中自大陆现今地壳运动的GPS研究. 科学通报 , 2001, 46(13): 1118–1120. Ma ZJ, Chen X L, Ye S H, et al. GPS study of current crustal movement in Chinese mainland. Chinese Science Bulletin (in Chinese) , 2001, 46(13): 1118-1120. |
| [5] | 顾国华. 中国地壳运动观测网络数据中心技术集成. 地震 , 2001, 21(4): 12–18. Gu G H. Integration of techniques at the data center for the crustal movement observation network of China. Earthquake (in Chinese) , 2001, 21(4): 12-18. |
| [6] | 甘卫军, 张锐, 张勇, 等. 中国地壳运动观测网络的建设及应用. 国际地震动态 , 2007(7): 43–52. Gan W J, Zhang R, Zhang Y, et al. Development of the crustal movement observation network of China and its applications. Research Developments in world Seismology (in Chinese) , 2007(7): 43-52. |
| [7] | 石耀霖, 朱守彪. 用GPS位移资料计算应变方法的讨论. 大地测量与地球动力学 , 2006, 26(1): 1–8. Shi YL, Zhu SB. discussion on method of calculating strain With GPS displacement data. Journal of Geodesy end Geodynamics (in Chinese) , 2006, 26(1): 1-8. |
| [8] | 赫尔墨特·莫里茨著, 宁津生等译.高等物理大地测量学.北京:测绘出版社, 1984.50~125 Helmot M. High Physics Geodetic Survey (in Chinese). Ning JS, et al. Trans. Beijing: Surveying and Mapping Press, 1984.50~125 |
| [9] | 江在森, 丁平, 王双绪, 等. 中国西部大地形变监测与地震预测. 北京: 地震出版社, 2001 : 7 -27. Jiang Z S, Ding P, Wang S X, et al. Telluric Deformation Monitoring and Earthquake Prediction in West China (in Chinese). Beijing: Seismological Press, 2001 : 7 -27. |
| [10] | 江在森, 张希, 祝意青. 昆仑山口西Ms8.1地震前区域构造变形背景. 中国科学(D缉) , 2003, 33(B04): 163–172. Jiang Z S, Zhang X, Zhu Y Q, et al. Regional tectonic deformation background before Ms8.1 earthquake on the west of Kunlun Mountain pass. Science in China (Series D) (in Chinese) , 2003, 33(B04): 163-172. |
| [11] | 杨国华, 江在森, 武艳强, 等. 中国大陆整体无净旋转基准及其应用. 大地测量与地球动力学 , 2005, 25(4): 6–10. Yang G H, Jiang Z S, Wu Y Q, et al. No-net rotation on crustal movement of china mainland and its application. Journal of Geodesy end Geodynamics (in Chinese) , 2005, 25(4): 6-10. |
| [12] | 江在森, 杨国华, 王敏, 等. 中国大陆地壳运动与强震关系研究. 大地测量与地球动力学 , 2005, 26(3): 1–9. Jiang Z S, Yang G H, Wang M, et al. On crustal movement in china continent and its relationship with strong earthquakes. Journal of Geodesy end Geodynamics (in Chinese) , 2005, 26(3): 1-9. |
| [13] | 陶本藻. 自由网平差与变形分析. 北京: 测绘出版社, 1984 : 14 -18. Tao B Z. Adjustment of Free Network and Analysis of Deformation (in Chinese). Beijing: Surveying and Mapping Press, 1984 : 14 -18. |
| [14] | 刘经南, 施闯, 许才军, 等. 利用局域复测GPS网研究中国大陆块体现今地壳运动速度场. 武汉大学学报·信息科学版 , 2001, 26(3): 189–195. Liu J N, Shi C, Xu CJ, et al. Present-day crustal movement speed field of China continent block using local repeated GPS network. Geomaiics and Information Science of Wuhan University (in Chinese) , 2001, 26(3): 189-195. |
| [15] | 刘经南, 施闯, 姚宜斌, 等. 多面函数拟合法及其在建立中国地壳平面运动速度场模型中的应用研究. 武汉大学学报·信息科学版 , 2001, 26(6): 500–508. Liu J N, Shi C, Yao Y B, et al. Hardy function interpolation and its applications to the establishment of crustal movement speed field. Geomaiics and Information Science of Wuhan University (in Chinese) , 2001, 26(6): 500-508. |
| [16] | 王琪, 张培震, 牛之俊, 等. 中国大陆现今地壳运动和构造变形. 中国科学(D辑) , 2001, 31(7): 529–536. Wang Q, Zhang P Z, Niu ZJ, et al. Present-day crustal movement and tectonic deformation in Chinese mainland. Science in China (Series D) (in Chinese) , 2001, 31(7): 529-536. |
| [17] | 王敏, 张祖胜, 许明元, 等. 2000国家GPS大地控制网的数据处理和精度评估. 地球物理学报 , 2005, 48(4): 817–823. Wang M, Zhang Z S, Xu M Y, et al. Data processing and accuracy analysis of national 2000'GPS geodetic control network. Chinese J. Geophys (in Chinese) , 2005, 48(4): 817-823. |
| [18] | Huang Jinli, Zhao Dapeng. High-resolution mantle tomography of China and surrounding regions. journal of Geophysical Research (B, Solid Earth) , 2006, 111(b9): B09305-1-B09305-21. |
| [19] | 江在森, 牛安福, 王敏, 等. 活动断裂带构造变形定量分析. 地震学报 , 2005, 18(6): 656–665. Jiang Z S, Niu A F, Wang M, et al. Quantitative analysis for tectonic deformation on active rupture zone. Acta Seismologica Sinica (in Chinese) , 2005, 18(6): 656-665. DOI:10.1007/s11589-005-0093-x |
| [20] | 江在森, 方颖, 武艳强, 等. 汶川8.0级地震前区域地壳运动与变形动态过程. 地球物理学报 , 2009, 52(2): 505–518. Jiang Z S, Fang Y, Wu Y Q, et al. The dynamic process of regional crustal movement and deformation before Wenchuan8. 0 earthquake. Chinese J. Geophys. (in Chinese) , 2009, 52(2): 505-518. |
| [21] | 江在森, 张希, 陈文胜, 等. 地形变资料求解应变值的尺度相对性问题研究. 地震学报 , 2000, 13(4): 375–383. Jiang Z S, Zhang X, Chen W S, et al. Study on scale dependence of strain value obtained from crustal deformation Data. Acta Seismologica Sinica (in Chinese) , 2000, 13(4): 375-383. DOI:10.1007/s11589-000-0019-6 |
| [22] | 杨国华, 黄立人. 速度面拟合法中多面函数几个特性的初步数值研究. 地壳形变与地震 , 1990, 10(4): 70–82. Yang G H, Huang L R. Primary numerical study of several characteristics about multi-surface function in fitting method of velocity surface. Crustal Deformation and Earthquake (in Chinese) , 1990, 10(4): 70-82. |
| [23] | 陶本藻, 王新洲, 于正林, 等. 用于垂直形变模型的多面函数拟合法的试验研究. 地壳形变与地震 , 1992, 12(1): 1–13. Tao B Z, Wamg X Z, Yu Z L, et al. An investigation on multiquadric fitting applied to modelling of vertical crustal movements. Crustal Deformation and Earthquake (in Chinese) , 1992, 12(1): 1-13. |
| [24] | 黄立人, 陶本藻, 赵承坤. 多面函数拟合在地壳垂直运动中的应用. 测绘学报 , 1993, 22(1): 21–28. Huang L R, Tao B Z, Zhao C K. The application of fitting method of multiquadric functions in research on crustal vertical movement. Acta Geodaeticaet Cartographica Sinica (in Chinese) , 1993, 22(1): 21-28. |
| [25] | 张希, 江在森. 用最小二乘配置获得地形变应变场动态图像的几个问题研究. 地壳形变与地震 , 1999, 19(3): 32–39. Zhang X, Jiang Z S. Study on some questions of dynamic pictures of crustal deformation and strain fields obtained by the least square collocation. Crustal deformation and Erhqake (in Chinese) , 1999, 19(3): 32-39. |
| [26] | 江在森, 马宗晋, 张希, 等. GPS初步结果揭示的中国大陆水平应变场与构造变形. 地球物理学报 , 2003, 46(3): 352–358. Jiang Z S, Ma Z J, Zhang X, et al. Horizontal strain field and tectonic deformation of China mainland revealed by preliminary GPS result. Chinese J. Geophys. (in Chinese) , 2003, 46(3): 352-358. |
| [27] | 武艳强, 江在森, 杨国华. 应用最小二乘配置球面解算GPS应变场的方法及应用. 地球物理学报 , 2009, 52(7): 1707–1714. Wu Y Q, Jiang Z S, Yang G H, et al. The application and method of GPS strain calculating in whole mode using least square collocation in sphere surface. Chinese J. Geophys (in Chinese) , 2009, 52(7): 1707-1714. DOI:10.3969/j.issn.0001-5733.2009.07.005 |
 2010, Vol. 53
2010, Vol. 53

