LEO(Low Earth Orbiting)GPS观测是崭新的、高效的地球大气层和电离层探测技术，通过GPS双频观测值获取的电离层总电子含量TEC(Total Electron Content)则是电离层探测和研究的一个重要参量.电离层是GPS信号的色散介质，会造成GPS信号传播的群延迟.GPS双频接收机接收的两个频率信号的群延迟是不同的，根据延迟的不同可以得到TEC^[1].GPS系统还具有时间分辨率高、可靠性高、可连续观测且成本低等优点，已成为测定电离层TEC的重要工具，前人在利用GPS系统提取TEC的精度问题上进行了大量的研究^[2~4].基于GPS卫星信号测量TEC时，由于GPS发射的信号在卫星和接收机两个频段存在时延，从而引起了TEC的计算偏差，被称为仪器偏差(Differential Code Biases，DCB).有计算结果表明，GPS仪器偏差最大可达7 ns(1 ns=2.86TECu)^[5].对于GPS接收机的仪器偏差，直接的解决方法是由接收机的生产厂家进行标定，但随着接收机运行环境的变化，仪器偏差可能会漂移，然而再由厂家标定，这对于GPS用户来说几乎不现实.国内外研究者为寻求高效的仪器偏差估计方法付出了巨大的努力.

国内外大量的文献讨论了GPS仪器偏差的计算方法:如采用多项式(球谐函数、广义三角数函数)拟合的方法建立电离层实测模型，把垂直TEC视作时间和经纬度的函数，联合解算出仪器偏差^[6~8]；另外，卡尔曼滤波方法也被应用于仪器偏差的解算^[5]；此外还有学者提出，在电离层小空间范围和短时间内变化缓慢的假设前提下，使用最小二乘解算出小区域内GPS接收机仪器偏差^[9].以上所有方法，都是假设电离层为距地面一定高度(H≤450 km)的单层实测模型，甚至假设电离层小空间范围和短时间内变化缓慢来估计仪器偏差.然而对于低轨卫星，由于其运动速度快(每秒可达数公里)，轨道高度一般都在400 km以上，以上假设都不适合低轨卫星接收机仪器偏差的解算.本文旨在尝试一种全新的LEO GPS接收机仪器偏差的解算方法:基于电离层球对称和1天内仪器偏差固定不变的假设，利用CHAMP和COSMIC原始观测数据，采用几何映射函数，通过最小二乘解算GPS接收机仪器偏差.

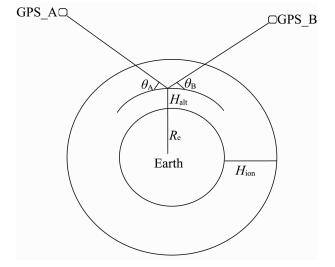
LEO与GPS几何位置如图 1所示.鉴于LEO轨道高度与其高动态特点，我们假设电离层球对称来获取GPS接收机仪器偏差，于是:

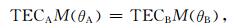
(1)

式中，M( )为映射函数，θ_A和θ_B为同时刻(历元)截止高度角.为满足不同位置天线(位于LEO天顶或前后端)的接收机仪器偏差解算，(1)式中较低的截止高度角也需参与计算(θ≥8°)，因此本文考虑使用几何映射函数(geometric mapping function)^[10]:

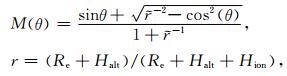
(2)

式中，R_e、H_alt和H_ion分别为地球半径、LEO轨道高度和电离层高度.

图 1

Fig. 1

图 1 LEO与GPS几何位置示意图 Fig. 1 Illustration of the geometry of LEO and GPS

我们采用载波相位平滑伪距(carrier to code leveling process)^[11]获取高精度TEC值.由GPS载波相位和伪距观测方程分别得到与TEC关系式:

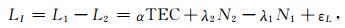
(3)

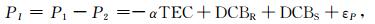
(4)

其中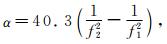，，f₁和f₂分别为载波相位L₁和L₂的频率；P₁和P₂为伪距观测量；λ₁、λ₂和N₁、N₂分别为两个载波的波长和整周模糊度；DCB_S和DCB_R分别为GPS卫星和接收机的仪器偏差；ε_L和ε_P分别为载波相位观测和伪距观测的噪声和多路径影响，且载波相位观测的噪声和多路径影响较伪距观测而言非常小，不到百分之一^[11].经数据预处理^[12]修复周跳和剔除粗差(野值)，视1天的DCB_R和DCB_S为常数，因此对于每个弧段，由式(2)和(3)可获得L_I+P_I的均值:

(5)

为剔除式(4)中的〈ε_P〉_arc影响，计算每个弧段L_I+P_I的RMS，并计算每个历元的L_I+P_I与〈L_I+P_I〉的差值，将其超过2倍RMS的观测值剔除，于是重新获得:

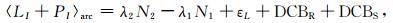
(6)

根据式(3)和式(5)，可得:

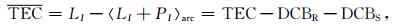
(7)

式中，各符号单位均为TECu.因此，由式(6)和式(1)可得:

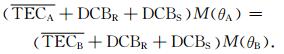
(8)

对于1天的观测值，我们可得到数万个匹配等式(8).根据最小二乘可解算出LEO仪器偏差(本文涉及到的GPS卫星仪器偏差DCB_S直接从CODE分析中心获取):

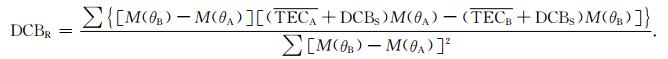
(9)

为减小电离层球对称假设引起GPS接收机DCB估计偏差，本文通过限制VTEC来实现.具体思路如下:

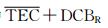
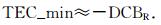
(1)找出1天中的最小值TEC_min，此时TEC因接近于零.由式(6)可获得粗略的仪器偏差值，

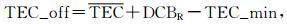
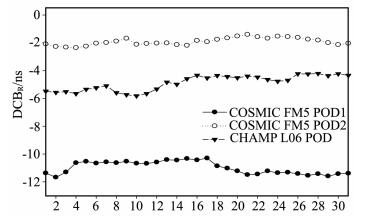
(2)令其粗略等于TEC(不包含任何仪器偏差)，再令VTEC=TEC_off*M(θ).对于CHAMP(轨道高度大约400 km)，本文选择的控制条件为VTEC＜12；而对于COSMIC(轨道高度大约800 km)，VTEC＜10.

为检验以上LEOGPS接收机仪器偏差估计方法的有效性，本文对不同天线位置和不同轨道高度的仪器偏差进行了解算，其中包括了CHAMP L06 POD(定位接收机，其天线位于卫星顶部)、COSMIC FM5 POD1和POD2(定位和电离层掩星接收机，天线位于LEO卫星前端和后端)，时间为:2008年1月1~31日，其计算结果如图 2所示.并统计分析如下:在2008年1月份期间，CHAMP和COSMIC仪器偏差变化最大幅度都在1.7 ns以内，分别为0.952 ns(COSMIC FM5 POD2)、1.378 ns(COSMIC FM5 POD1)和1.603 ns(CHAMP L06 POD)；并且在此期间，仪器偏差标准差(内符合精度)都在0.6 ns以内，依次分别为0.262 ns，0.451 ns和0.547 ns.可见，通过以上方法估计的仪器偏差都较稳定，可获得较好的估计结果.然而，相比较CHAMP接收机仪器偏差估计结果，COSMIC估计结果更加稳定.

图 2

Fig. 2

图 2 LEO GPS接收机DCB估计结果时序图 Fig. 2 The time series of estimated results of LEO GPS receiver DCB

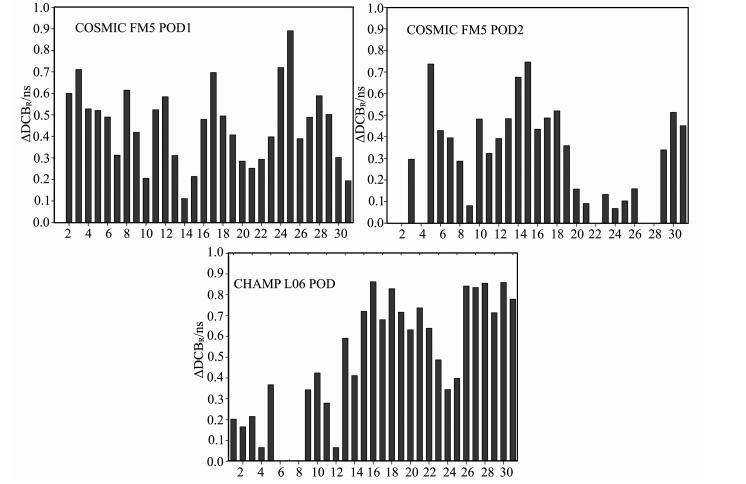
COSMIC网站(http://www.cosmic.ucar.edu/)对全球发布了其与CHAMP仪器偏差每天的估计结果，为进一步检查上述估计结果的准确性，我们将它们进行了比较.图 3为本文估计结果与COSMIC公布结果差分绝对值，差值为0时表示COSMIC没有发布当天结果.

图 3

Fig. 3

图 3 GP SLEO接收机DCB估计结果与COSMIC公布结果差分绝对值示意图 Fig. 3 The absolute difference between the estimated results of LEO GPS receiver DCB and those from COSMIC

相比COSMIC网上(以其结果为真值)公布的结果，2008年1月份期间的标准偏差(外符合精度)都在0.6 ns以内，分别为0.415 ns(COSMIC FM5 POD2)、0.453 ns(COSMIC FM5 POD1)和0.596 ns(CHAMP L06 POD)，其与上述各LEO卫星仪器偏差内符合精度趋势(由高到低)完全一致.从以上统计结果可知，本文采用的仪器偏差估计方法都可获得较好的估计结果.并且，COSMIC FM5的估计精度优于CHAMP L06估计精度，并COSMIC FM5 POD2优于COSMIC FM5 POD1.我们分析，主要有以下2个原因导致估计精度相差较大:其一为LEO卫星轨道高度. LEO卫星轨道高度越低，其GPS信号受电离层影响也就越大，因此受到电离层球对称的影响就越显著.虽然本文对其影响进行了适当的控制，但其还是时刻存在.因此，无论是外符合精度还是内符合精度，COSMIC FM5(轨道高度大约800 km)估计结果都要优于CHAMP L06(轨道高度大约400 km)的估计结果.其二为匹配等式(8)的数目.COSMIC FM5 POD2每天获得的观测值远大于COSMIC FM5 POD1，其匹配等式(8)可达到十万以上，而COSMIC FM5 POD1的匹配等式只有数万个，因而COSMIC FM5 POD2结果优于COSMIC FM5 POD1的结果.

本文基于电离层球对称假设，利用CHAMP和COSMIC原始观测数据，采用几何映射函数，通过最小二乘解算了2008年1月份期间CHAMP POD、COSMIC FM5 POD1及COSMIC FM5 POD2 GPS接收机仪器偏差，并与COSMIC网上公布的结果进行了比较，得出以下结论:

(1)在2008年1月份期间，通过以上方法估计的仪器偏差，其变化最大幅度都在1.7 ns以内，内外符合精度都在0.6 ns以内.由此可知，通过此方法估计的仪器偏差较为稳定，可获得较好结果.

(2)COSMIC PM5仪器偏差估计结果优于CHAMP L06的结果，并CHAMP L06 POD结果优于CHAMP L06 OCC1的结果.经过严密的数据预处理后(剔除粗差和修复周跳及消除多路径影响)，电离层球对称假设是仪器偏差估计的最大误差源.不同的轨道高度，电离层球对称影响不同.轨道越高，电离层球对称假设导入的误差越小.

纵观国内外有关仪器偏差估计的文献，都是假设其1天内固定不变，本文也不例外.实际上，因为1天内LEO卫星多次交替位于日面和夜面，GPS接收机温度变化较大，仪器偏差也会受温度的变化而变化，但无文献报道研究，这也是我们亟需有待解决的问题.