探地雷达(Ground Penetrating Radar, 简称GPR)是采用高频电磁波在地下电性界面(目标体)上的反射与透射信息来探测地质目标体的一种地球物理方法[1].具有高效、快速、无损、抗干扰能力强的优点, 广泛应用于工程与环境地球物理探测的各个领域, 成为浅部勘探的重要方法技术[2].探地雷达正演模拟对数据解释具有重要的指导作用.通过模型正演模拟, 可以加深对探地雷达探测剖面的认识, 提高解释精度.常用的正演模拟方法有矩量法(MOM)[3], 有限元法(FEM)[4], 边界元法(BEM), 时域有限差分(Finite Difference Time Domain, FDTD)法[5]等.时域有限差分方法计算程序具有通用性强、适合并行运算、简单直观易掌握等优点而被广泛应用.
国内外学者对探地雷达时域有限差分正演模拟做了大量的研究.Wang等[6, 7]研究了三维时域有限差分法的探地雷达正演模拟, 采用廖氏吸收边界条件, 可解决非垂直透射问题, 但编程复杂, 需储存信息量大[8]; Gurel[9]在理论上对三维探地雷达建模进行了研究; Irving[10]采用PML吸收边界研究了二维探地雷达数值模拟, 并展示了TM、TE模式的探地雷达模拟研究成果; Zhan等[11]进行了二维/三维探地雷达的桥面检测研究; 国内学者王建等[12]、冯德山等[13]、薛桂霞等[14]进行了二维时域有限差分法探地雷达模拟; 刘四新和曾昭发[15]完成了频散介质中地质雷达波传播的数值模拟; 王兆磊和周辉[16]完成了利用FDTD方法及探地雷达数据资料反演二维地下介质的研究, 都取得了较好的成果.
在时域有限差分法进行探地雷达模拟研究中, 前人多进行二阶精度的中心差分近似, 且采用PML边界条件, 实现复杂, 不便于推广应用.二阶中心差分近似算法简单, 但数值色散误差较大, 在模拟复杂模型时不能较好地表现目标体的精细电磁响应变化[17].目前解决数值色散影响主要是通过减小离散网格的时间和空间步长, 这将增加计算网格数目和计算时间, 导致计算机所需存储空间增大, 计算效率低[18, 19], 使得FDTD方法在复杂介质模拟应用中受到一定限制.高阶FDTD法能有效地改善数值色散问题, 能够对复杂介质进行有效模拟.Fang[20]提出了FDTD (2, 2M)法, 即在时间上采用二阶精度的离散格式, 而在空间上采用高阶精度的离散格式, 大大改善了FDTD方法的数值色散, 提高了计算精度, 而且还保留了传统方法中简单、直观和容易掌握的特点, 能够有效地节省计算资源, 提高电磁场的时域模拟计算效率.之后也有大量学者采用这种高阶有限差分方法进行模拟研究, 如Young[21]获得了等离子体辐射情况下(2, 4)阶差分与(2, 2)阶反射误差对比分析; Lan等[22]在电磁兼容研究方面, 进行FDTD (2, 4)理论推导, 并分析模拟结果; Georgakopoulos[23]在电磁散射模拟中对高阶FDTD法的理论进行了研究, 并对(2, 2)与(2, 4)阶差分的误差进行比较; Sun[24]提出了二维FDTD (2, 4)阶方法的亚网格技术; 吴丰收[25]完成了二维FDTD (2, 2M)探地雷达正演模拟, 在模拟精度上取得了较好的效果.
关于高阶FDTD法的稳定性, 数值色散及吸收边界条件前人也做了许多研究[26~31], 但目前高阶FDTD方法的应用研究多集中于电磁仿真领域, 在探地雷达正演模拟方面高阶FDTD方法研究甚少.为了提高探地雷达正演模拟的精确度及改善二维模拟的准确性, 本文在结合前人研究的基础上, 开展三维探地雷达高阶FDTD方法的数值模拟研究, 采用UPML吸收边界[32~34], 大大降低边界上的反射, 提高探地雷达模拟精度.UPML吸收边界避免在吸收介质中对电磁场的分裂, 能够吸收外向传播波和凋落波, 保留了PML技术优点, 降低了对内存的需求, 并且易于编程, 计算效率更高.但常规的UPML吸收边界是空间二阶差分近似, 不能直接应用到高阶时域有限差分, 因此本文将推导出UPML吸收边界的高阶FDTD形式并在实际模拟加以验证.
2 高阶FDTD方法二阶精度FDTD方法采用两点中心差分对时间和空间的一阶导数进行近似.高阶FDTD方法就是以时域差分方程为基础将场量进行Taylor展开得到一组新的差分方程.由Taylor级数展开定理, 任意点处的函数值都可以由参考点x0处的函数值和其导数值来表示:
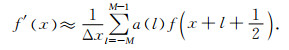
|
(1) |
二阶FDTD方法对时间-空间求一阶导数时, 采用了具有二阶近似精度的中心差分.如果采用高阶中心差分法近似, 可以将传统的FDTD方法扩展到时间和空间均具有高阶精度的算法, 即FDTD (2N, 2M).在对时间进行高阶差分时涉及到多个时间点的数据, 使得储存量成倍增加, 而在计算精度方面对结果的贡献不大且计算效率低[19], 对于较大的模型计算相当耗时.所以本文仅讨论三维空间高阶FDTD (2, 2M)差分形式.
运用Yee网格模型, 时间离散采用二阶中心有限差分格式, 空间离散采用2M阶中心有限差分格式, 则可得到离散化后的麦克斯韦方程(以Ex, Hx为例):
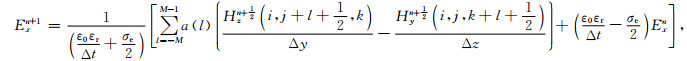
|
(2) |
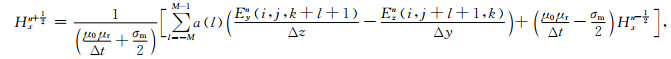
|
(3) |
式中, ε0, μ0分别为真空中的介电常数和磁导率, εr, μr分别为相对介电常数和相对磁导率, σe为电导率, (σm为磁阻率, △x、△y、△z分别为沿x, y, z方向的网格大小i, j, k分别为沿x, y, z方向的网格序号, a(l)为
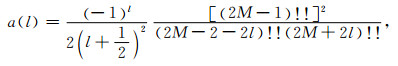
|
数值稳定性条件:
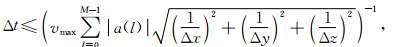
|
(5) |
vmax为计算空间中的电磁波最大传播速度.取△x=△y=△z时, (1~5)式的简化形式为
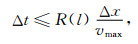
|
(6) |
其中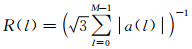
|
|
表 1 Courant稳定条件系数R(l) Table 1 Courant stability condition coefficient |
Gedney[32]和Sacks[34]提出了单轴各项异性完美匹配吸收边界(UPML)条件, 它的实现不需要电磁场分裂, 算法更简洁, 便于理解和实现.本文推导出了UPML吸收边界在高阶FDTD中的迭代公式并应用于模拟, 由Maxwell旋度方程:
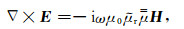
|
(7) |
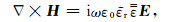
|
(8) |
式中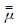
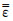
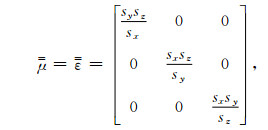
|
(9) |
以(8)式为例, 写成差分形式:

|
(10) |
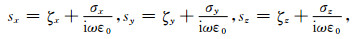
|
(11) |
为了便于进行迭代, 通过引人中间变量的方法实现, 这里以Ex为例说明(H分量与之类似), 令
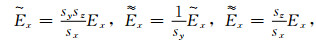
|
(12) |
则, 式(10)中的第一行各分量通过中间变量可化为
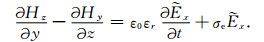
|
(13) |
上述FDTD差分格式刷新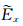
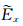
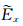
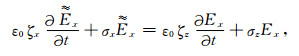
|
(14) |
通过当前及上一时刻的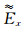
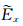
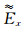
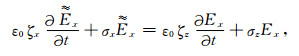
|
(15) |
通过当前及上一时刻的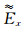

|
(16) |
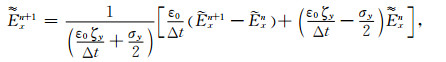
|
(17) |
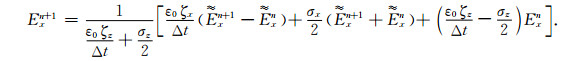
|
(18) |
其他电磁场分量的差分格式可以类似得到.
σx、σy和ζx、ζy的取值是逐层变化的, 即按照一定的规律由UPML层的内表面沿法线方向向UPML外层递增.以x方向的参数设置为例, 由x=0到x=d按照[35]
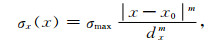
|
(19) |
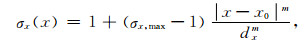
|
(20) |
进行渐变.上式中
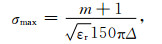
|
(21) |
Δ为网格边长, dx为UPML吸收边界厚度, x0为UPML层内表面位置, 由Gedney研究表明, 当m=4, σx, max=5[36]时为最佳.
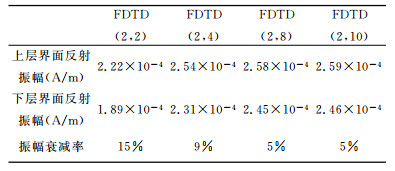
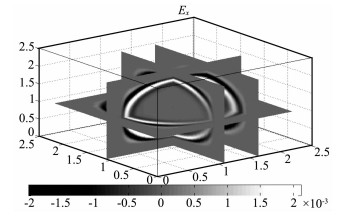
4 精度验证为了验证UPML吸收边界的效果, 取大小为1.5m×1.5m×1.5 m的均匀全空间模型, 介质为空气, 模型网格空间步长为Δx=Δy=Δz=0.01m.中心频率为1 GHz的Ricker子波波源置于模型中心, 源振幅A0为1 A/m; 时间步长为Δt=1.0×10-11.图 1是空气介质时UPML边界Ex分量的三维快照切片图, 从中可以看出在各个方向能很好地吸收到达边界的能量.各阶UPML吸收边界反射波振幅比较见表 2, 可以看出, UPML边界条件能够有效地吸收到达截断边界的能量, 随着阶数的增加界面反射逐渐减弱, FDTD (2, 10)时界面的反射振幅仅为FDTD (2, 2)时的1/3, 显示了不错的吸收的效果.
|
图 1 UPML吸收边界三维切片图 Fig. 1 Three-dimension slices of UPML absorbing boundary |
|
|
表 2 高阶UPML吸收边界的吸收效果 Table 2 The effect of UPML absorbing boundary |
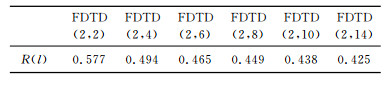
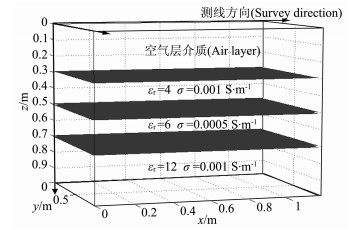
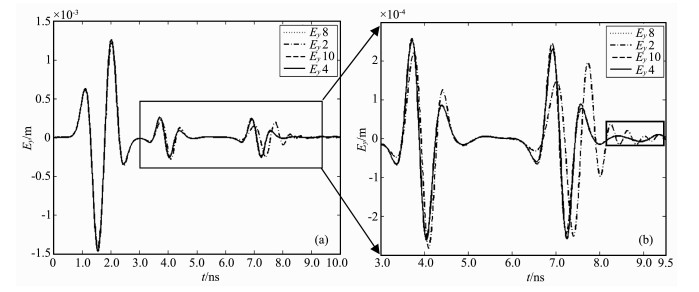
为了验证高阶FDTD的模拟精度, 给出一个三层层状模型(图 2), 采用Ricker子波作为激励源, 点源位于空气层与介质的分界面处.网格空间步长为Δx=Δy=Δz=0.01m, 分别采用二阶及高阶差分进行模拟计算并抽取单道回波信号, 各阶单道回波振幅曲线如图 3所示.可以看出高阶与二阶FDTD空气直达波波形相似, 分层界面反射波幅有明显的差异.表 3是各阶差分单道信号分层界面反射波振幅比较, 从中可以看出, 随着差分阶数的增加, 界面反射振幅逐渐增强, 且下层界面反射振幅衰减逐渐减弱, 表明在有耗介质中传播时, 高阶相比二阶其信号反射特性更强, 另外在图 3b中单道信号曲线对比中, 在介质区域内传播时, 高阶FDTD的波形也比二阶更为平稳, 显示了较少的误差干扰.
|
图 2 层状介质模型 Fig. 2 The model of layered media and its parameters |
|
图 3 层状介质模型各阶单道信号曲线(b图为a图方框部分的放大显示) Fig. 3 The single-trace signal of layered model (b map is part of the zoom box) |
|
|
表 3 各阶单道信号界面反射波振幅比较 Table 3 The single-trace reflection amplitude at interface |
高阶差分在每一个网格点上, 各场分量不但与该点前一时间步长的值及该点周围半网格处另一场分量值有关, 并且随着差分阶数的增加, 每一点的计算涉及到更多的场分量.因此高阶FDTD法比传统FDTD法精度高.但相应的计算量也增加, 计算机耗时也随着增加.虽然高阶比传统二阶更耗时, 但其对精度的提高显而易见, 这也是目前正演模拟中提高精度最直接有效的方法.随着现代计算机的高速发展以及电磁场并行计算技术的完善, 这一问题也会得到很好的解决.
从图 3中可以看出(2, 8)阶与(2, 10)阶的单道信号曲线已基本吻合, 说明当阶数达到一定范围后, 计算精度的差异已经很小.在实际模拟中应该根据具体情况选取合适的阶数, 这样在计算精度及计算速度上均能达到不错的效果.
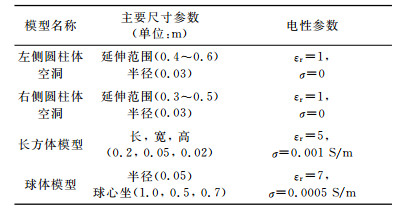
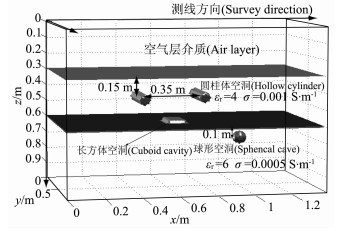
5 数值模型算例复杂三维探地雷达正演实例选用层状介质含圆柱体空洞、球体以及长方体的地电模型.模型示意如图 4所示, 模型具体参数设置如表 4所示.网格空间步长为0.01m, 脉冲源为中心频率1GHz的Ricker波, 时窗长度为12 ns.天线位置位于空气介质与地层的分界面处, 测线沿x轴方向, 采用发射天线与接收天线分离的方式, 收发距为0.15 m.
|
图 4 三维模型示意图 Fig. 4 The sketch map of 3D model |
|
|
表 4 三维模型参数说明 Table 4 Description parameter s of 3D model |
为了进一步验证高阶FDTD在计算精度上的优势, 对图 4中的复杂模型在相同设置条件下分别采用二阶和高阶差分进行模拟计算.为了突出高阶差分对复杂模型的精细变化, 设定下层长方体及球体模型与周围介质电性参数接近.
图 5和图 6是不同极化方式不同差分阶数正演模拟切片图.从图中可以看出:由于天线的极化特性使得模型中沿y方向延伸的目标体在YY极化剖面上比在XX极化剖面上更清晰.图 5YY极化方式计算中, 相对于低阶差分, 八阶差分模拟的雷达剖面, 下层球体、长方体模型反射波信号更强, 更准确地显示了其位置.图 6XX极化方式计算中, 各阶差分差异不明显.所以, 在三维模拟中, 对于复杂目标体探测, 应结合高阶差分及目标体延伸选择合适的极化方式方能达到最佳的模拟精度.
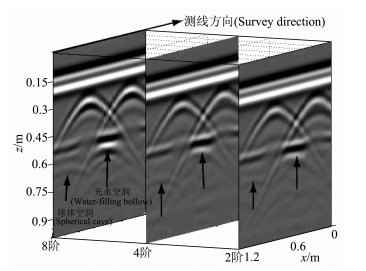
|
图 5 YY极化不同阶精度探地雷达模拟剖面 Fig. 5 Comparison of the GPR profiles with different order by YY polarization |
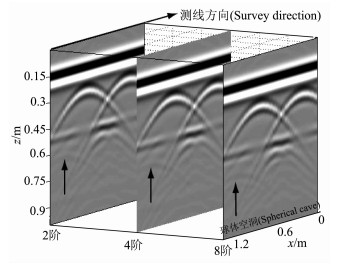
|
图 6 XX极化不同阶精度探地雷达模拟剖面 Fig. 6 Comparison of the GPR profiles with different order by XX polarization |
图 7为采用8阶差分计算所得测线在y=0.3m, 0.4, 0.5, 0.6m处的剖面图; 比较不同测线的雷达剖面图可以清晰地看出目标模型的分布能很好的显示上层圆柱体空洞的延伸范围和位置分布, 下层界面除了上层圆柱体空洞正中心对应位置信号较弱外其余部分均能较好显示分层性.虽然圆柱体空洞产生的绕射波干扰了下层介质中目标体的反射, 但仍然可以清晰地定位球体及长方体模型的分布位置及延伸情况.为了多角度定位目标体, 以y方向布置测线, 突出反映目标体走向方向的延伸情况.图 8为x=0.5, 0.7, 0.9m处8阶差分计算所得雷达剖面图, 从中可以看出圆柱体空洞、长方体模型沿y方向的延伸范围; 结合x, y方向的雷达剖面可以对三维目标体的分布位置进行很好的定位.以上图像显示结果均与模型设置的分布范围吻合, 显示了高阶差分对探测复杂模型的准确性.
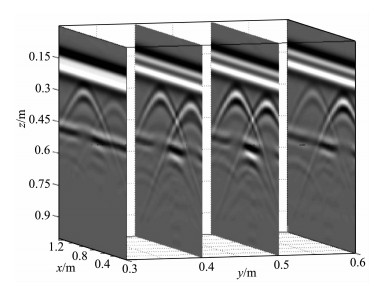
|
图 7 测线探地雷达切片图y=0.3 m, 0.4 m, 0.5 m, 0.6 m Fig. 7 Comparison of the GPR slices at y=0.3 m, 0.4 m, 0.5 m, 0.6 m |
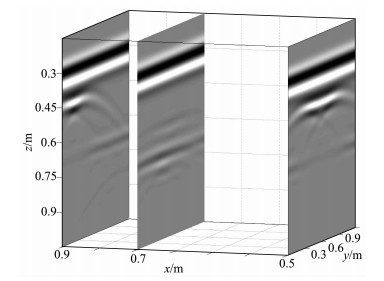
|
图 8 测线探地雷达切片图, x=0.5 m, 0.7 m, 0.9 m Fig. 8 Comparison of the GPR slices at x=0.5 m, 0.7 m, 0.9 m |
从正演模拟结果可见, 高阶有限差分在复杂模型的模拟中具有较高的精度, 能够清晰准确地反映出目标体的位置分布.对于三维正演模拟, 通过各种立体三维切片图显示, 能形象直观地反映出目标体的空间分布位置及沿伸情况, 更全面与细致地了解雷达波的空间反射特征, 提高了探地雷达探测的准确性与精确度, 为三维探地雷达探测与解释技术的开展打下基础.
6 结语本文介绍了三维高阶时域有限差分探地雷达正演模拟的实现方法, 推导了适合高阶差分的UPML吸收边界公式, 对比分析了高阶与传统二阶差分在模拟精度及计算效率上的差异.通过比较时域有限差分正演模拟结果表明:三维高阶时域有限差分改善了常规二阶差分的数值色散问题, 提高了模拟精度; 虽然高阶比传统二阶更耗时, 但在提高精度方面效果显著.随着现代计算机的高速发展以及电磁场并行计算技术的完善, 高阶FDTD法将得到更广泛的应用.
| [1] | Kowalsky M B, Dietrich P, Teutsch G, et al. Forward modeling of ground-penetrating radar data using digitized outcrop images and multiple scenarios of water saturation. Water Resources Research , 2001, 37(6): 1615-1625. DOI:10.1029/2001WR900015 |
| [2] | 曾昭发, 刘四新, 王者江, 等. 探地雷达方法原理及应用. 北京: 科学出版社, 2006 : 207 -238. Zeng Z F, Liu S X, Wang Z J, et al. Method Principle and Application of GPR (in Chinese). Beijing: Science Press, 2006 : 207 -238. |
| [3] | Harrington R F, Mautz J R. Theory of characteristic modes for conducting bodies. IEEE.Trans.on AP , 1971, 19(6): 622-628. |
| [4] | 底青云, 王妙月. 雷达波有限元仿真模拟. 地球物理学报 , 1999, 42(6): 818–825. Ding Q Y, Wang M Y. 2D finite modeling for radar wave. Chinese J.Geophys. (in Chinese) , 1999, 42(6): 818-825. |
| [5] | Yee K S. Numerical solution of initial boundary value problems involving Maxwell's equation in isotropic media. IEEE.Trans.AP , 1966, 14(5): 302-307. |
| [6] | Wang Tsili, Alan C Tripp. FDTD simulation of EM wave propagation in 3-D media. Geophysics , 1996, 61(1): 110-120. DOI:10.1190/1.1443930 |
| [7] | Wang Tsili, Alan C Tripp. A finite-difference time domain solution for three-dimensional electromagnetic modeling. Geophysics , 1993, 58(6): 797-809. DOI:10.1190/1.1443465 |
| [8] | Moghaddam M, Chew W C. Stabilizing Liao absorbing boundary conditions using single-precision arithmetic. IEEE.AP-S , 1991, 1: 430-433. |
| [9] | Levent Gurel. Thre-dimensional FDTD modeling of a ground-penetrating radar. IEEE.Transactions on Geoscience and Remote Sensing , 2000, 38(4): 1513-1522. DOI:10.1109/36.851951 |
| [10] | Irving James, Rosemary Knight. Numerical modeling of ground-penetrating radar in 2-D using MATLAB computers. Geosciences , 2006, 32: 1247-1258. |
| [11] | Zhan H, Belli S K. Effectiveness of 2D FDTD ground pentrating radar modeling for bridge deck deterioration evaluated by 3D FDTD. IEEE.Geosaence and Remote Sensing Symposium (IGARSS) , 2008: 1330-1334. |
| [12] | 王建, 彭仲秋, 谢处方. 地下目标瞬时散射的时域有限差分法数值模拟. 地球物理学报 , 1996, 39(1): 349–357. Wang J, Peng Z Q, Xie C F. Numerical simulation of transient scatiering by underground target with FDTD method. Chinese J.Geophys.(Acta Geophysica Sinica) (in Chinese) , 1996, 39(1): 349-357. |
| [13] | 冯德山, 戴前伟, 何继善, 等. 探地雷达GPR正演模拟的时域有限差分实现. 地球物理学进展 , 2006, 21(2): 630–636. Feng D S, Dai Q W, He J S, et al. Finite difference time domain method of GPR forward simulation. Chinese J.Progress in GeoPhysics (in Chinese) , 2006, 21(2): 630-636. |
| [14] | 薛桂霞, 王鹏. 探地雷达时域有限差分法正演模拟. 物探与化探 , 2006, 30(3): 234–239. Xue G X, Wang P. The application of the FDTD method to GPR simulation. Chinese J.Geophysical & Geochemical Exploration (in Chinese) , 2006, 30(3): 234-239. |
| [15] | 刘四新, 曾昭发. 频散介质中地质雷达波传播的数值模拟. 地球物理学报 , 2007, 50(1): 320–326. Liu S X, Zeng Z F. Numerical simulation for ground penetrating Radar wave propagation in the dispersive medium. Chinese J.Geophys. (in Chinese) , 2007, 50(1): 320-326. |
| [16] | 王兆磊, 周辉, 李国发. 地质雷达数据资料反演二维地下介质的方法. 地球物理学报 , 2007, 50(3): 897–904. Wang Z L, Zhou H, Li G F. Inversion of ground-penetrating radar data for 2D electric parameters. Chinese J.Geophys. (in Chinese) , 2007, 50(3): 897-904. |
| [17] | Jose M Carcione. Radiation patterns for 2-D GPR forward modeling. Geophysics , 1998, 63(2): 424-430. DOI:10.1190/1.1444342 |
| [18] | Lan Kang, Liu Yaowu, Lin Weigan. A higher order (2, 4) scheme for reducing dispersion in FDTD algorithm. IEEE.Trans on EMC , 1999, 41: 160-165. |
| [19] | 王建永, 赵长青, 陈秉岩. FDTD (2M, 2N)的一种实现方法. 成都信息工程学院学报 , 2006, 21(4): 559–562. Wang J Y, Zhao C Q, Chen B Y. An implementation method of FDTD (2M, 2N). Chinese J.Chengdu University of Information Technology (in Chinese) , 2006, 21(4): 559-562. |
| [20] | Fang J.Time domain finite difference computation for Maxwell's equations[Ph.D.thesis].CA:University ofCalifornia at Berkeley, 1989 |
| [21] | Jeffrey L Young. A higher order FDTD method for EM propagation in a collisionnless cold plasma IEEE. Transactions on Antennas and Propagation , 1996, 44(9): 1283-1290. DOI:10.1109/8.535387 |
| [22] | Lan Kang, Liu Yao-wu. A Higher Order (2, 4) Scheme for reducing dispersion in FDTD algorithm. IEEE Transactions on Elearomagnetic Compatibility , 1999, 41(2): 160-166. DOI:10.1109/15.765109 |
| [23] | Georgakopoulos Stavros V, Birtcher Craig R, et al. Higherorder finite difference schemes for electromagnetic radiation scattering and penetration IEEE. Antenna's and Propagation Magazine , 2002, 44: 134-142. DOI:10.1109/74.997945 |
| [24] | Sun Shu-hai, Charles T. A new subgridding scheme for FDTD (2, 2) and FDTD (2, 4) methods. IEEE.Transactions on magnetics , 2004, 40: 1041-1045. DOI:10.1109/TMAG.2004.824910 |
| [25] | 吴丰收, 曾昭发, 黄玲, 等. 探地雷达信号的高阶时间域有限差分模拟. 物探化探计算技术 , 2009, 31(4): 308–313. Wu F S, Zeng Z F, Huang L. Using higher-order FDTD for ground penetrating Radar response simulation. Chinese J.Computing Techniques for Geophysical and Geochemical Exploration (in Chinese) , 2009, 31(4): 308-313. |
| [26] | Nader Farahat, Sergey Yuferev. High order surface impedance boundary conditionsfor the FDTD method. IEEE.Transactions on Magnetics , 2001, 37(5): 3242-3247. DOI:10.1109/20.952586 |
| [27] | Hadi M F, Piket-May M. Amodified FDTD (2, 4) scheme for modeling electrieally large struetures with high-phase aceuraey. IEEE.Trans.Antennas Propagat. , 1997, 45(2): 254-264. DOI:10.1109/8.560344 |
| [28] | Zygiridis Theodoros T, Tsiboukis Theodoros D. Lowdispersion algorithms basedonthe higher order (2, 4) FDTD method. IEEE.Trans.Microwa Veand Teehniques , 2004, 52(4): 1321-1327. DOI:10.1109/TMTT.2004.825695 |
| [29] | EI-Raouf Hany E Abd, EI-Diwani Esam A, Ammar Abd El-Hadi, et al. Alow-dispersion 3-D second-order in time fourth-order in spaee FDTD seheme (M3d_(24)). IEEE.Trans.Antennas Propagat. , 2004, 52(7): 1638-1645. DOI:10.1109/TAP.2004.831286 |
| [30] | Zygiridis Theodoros T, Tsiboukis Theodoros D. A.Dispersion-reduetion scheme for the higher order FDTD (2, 4) method. IEEE.Trans.Magneties , 2004, 40(2): 1464-1467. DOI:10.1109/TMAG.2004.824779 |
| [31] | Tirkas Panayiotis A. Higher order absorbing boundary conditionsfor the finite difference time domain method. IEEE.Transactions on Antennas and Propagation , 1992, 40(10): 1215-1223. DOI:10.1109/8.182454 |
| [32] | Gedney S D. An anisotropic perfectly matched layerabsorbing medium for the truncation of FDTD lattices. IEEE.Trans.Antennas Propagat. , 1996, 44(12): 1630-1639. DOI:10.1109/8.546249 |
| [33] | Gedney S D. An anisotropic PML absorbing media for the FDTD simulation of fields in lossy and dispersive media. Electromagnetics , 1996, 16(4): 399-415. DOI:10.1080/02726349608908487 |
| [34] | Sacks Z S, Kingsland D M, Lee J F. A perfectly matched anisotropic absorber for use as an absorbing boundary condition. IEEE.Trans.Antennas Propagat. , 1995, 43(12): 1460-1463. DOI:10.1109/8.477075 |
| [35] | Francis H. Drossaert, Antonios Giannopoulos. A nonsplit complex frequency-shifted PML based on recursive integration for FDTD modeling of elastic waves.Geophysics , 2007, 72(2): 9-17. |
| [36] | Hastings F D, Schneider J B, Broschat S L. Application of the perfectly matched layer (PML) absorbing boundary condition to elastic wave propagation. Journal Acoustical Society of America , 1996, 100(5): 3061-3069. DOI:10.1121/1.417118 |
 2010, Vol. 53
2010, Vol. 53