2. 中国石油东方地球物理公司, 河北涿州 072751
2. Bureau of Geophysical Prospecting, CNPC, Hebei Zhuozhou 072751, China
多次反射是反射地震勘探, 特别是海洋地震勘探中普遍存在的最突出的问题之一.目前的地震成像方法主要还是基于一次反射波能量, 多次波的存在会掩盖一次反射波, 有时会被误认为是一次反射波, 干扰一次反射波的成像, 因此多次波的衰减仍然是一个非常重要的研究课题.对于海洋油气勘探和复杂的陆地勘探, 如何有效地进行叠前多次波压制是地震资料处理的一个难点.鉴于多次波对地震资料处理的诸多影响, 众多地球物理学家们不断地提出了各种新的压制多次波的方法[1~4].然而不同的多次波压制方法存在不同的假设和先验条件, 当满足这些假设条件时就会取得好的压制效果, 否则就会失败, 因此多次波压制一直是一个亟待解决的问题.目前, 多次波的衰减方法大致可以分为两大类[5]:一类是基于有效波和多次波之间差异的滤波方法; 另一类是基于波动方程的预测减去法, 通过波场模拟或反演地震数据来预测多次波, 然后把它从原始地震数据中减去.
滤波类方法利用一次反射波和多次波在时间和空间特征上存在的差异, 通过不同的变换方法, 分离一次波和多次波, 然后从原始数据中滤去多次波.目前所认识到的一次波和多次波之间的差异性主要有周期性和动校时差差异性.
基于多次波的周期性, Robinson引人维纳滤波来压制多次波[6], 这种方法对于1-D, 特别是在线性Radon域效果明显[7].Backus利用预测反褶积来消除海上鸣震[8], 这种方法在压制浅海短周期多次波时比较有效.利用一次波和多次波的剩余时差(动校速度)差异衰减多次波的方法有Radon滤波[9, 10], 聚束域滤波[11], F-K滤波[12], K-L滤波[12], 共中心点叠加[12]等.
波动方程方法压制多次波是通过使用波动方程反演预测出多次波, 预测的多次波通过自适应匹配滤波后从地震记录中减去.目前, 基于波动方程来压制多次波的方法主要有三种[5]:波场外推法[13]、反馈迭代法[14], 逆散级数法[15].多次波的预测按照是否需要先验信息分为模型驱动和数据驱动方法.模型驱动方法预测多次波是通过使用一些模型信息(比如海底深度、海底反射系数和海水速度等), 根据波场的动力学特征按照声波波动方程模拟出多次波的方法, 波场外推法属于模型驱动方法.数据驱动方法预测多次波是直接使用观测到的地震数据, 根据波动方程叠前反演出多次波, 这种方法不需要先验及后验信息, 反馈迭代法和逆散射级数法属于数据驱动的方法.波动方程多次波衰减方法能适用于复杂的地下结构, 需要较少或不需要关于地下结构的假定, 因此它可以预测出更多类型的多次波, 能在较少损坏一次反射信号的情况下压制多次波.
波动方程方法先预测出多次波, 但预测出的多次波和记录中的多次波通常是不匹配的, 它们在振幅、相位及到时上会存在差异, 需要通过估计滤波因子来匹配记录中的多次波和预测出的多次波, 然后从记录中减掉多次波.常见的匹配滤波方法有最小二乘自适应匹配[14, 16, 17]、基于1范数最小单道自适应匹配[18]、基于独立变量分析自适应匹配[19]、模式识别匹配[20]、2D歼灭匹配滤波[21]、基于反演的方法[22]等.不同的匹配方法存在不同的假设条件, 各有其优缺点.本文主要针对1范数最小单道自适应匹配和最小二乘匹配以及1范数最小均衡多道自适应匹配进行对比研究.最小二乘匹配滤波方法基于2范数准则, 在多次波衰减后的一次波2范数最小意义下估计滤波因子实现匹配, 该方法存在两个隐含假设条件:也震记录中的一次波与多次波是正交的; 多次波衰减后的地震记录满足能量最小.为了改善多次波和一次波的正交性, 人们不断地提出了频率域最小能量优化、时间域单道维纳滤波[14, 23]、伪多道维纳滤波[24]、多道维纳滤波、扩展多道维纳滤波[16]、均衡多道维纳滤波、均衡伪多道维纳滤波[17]等, 这些方法能够在一定程度上减弱对输人数据的多次波和有效波的正交性的要求, 但是仍然不能避免多次波衰减后的地震记录能量最小的假设.比如, 当很强的有效波被很弱的多次波包围时, 为了使衰减多次波后的地震记录能量最小, 多次波将会同时匹配多次波和有效波, 部分有效波被当成多次波衰减掉.为了避免衰减多次波后的地震记录能量最小的假设条件, Gmtton[18]提出基于1范数最小单道自适应匹配滤波方法, 因为1范数对大的异常保持稳健, 但是1范数最小单道自适应匹配滤波方法仍然对输人数据的多次波和有效波的正交性的条件有一定要求.基于1范数和2范数匹配各自的优缺点, 本文提出了1范数和2范数混合的均衡多道自适应匹配滤波方法, 该方法首先能够避免衰减多次波后的地震记录能量最小的假设条件, 同时进一步避免了输人数据的多次波和有效波正交性的假设条件, 所以这种方法能够取得比较好的匹配效果, 而且计算速度和单道1范数最小自适应匹配相同.
2 方法原理 2.1 单道最小二乘自适应匹配滤波Versuur[23]采用的频率域单道最小二乘自适应匹配滤波, Berkhout[14], Weglein[15]采用时间域单道最小二乘自适应匹配滤波来消除子波因素.
设d(t)(r=1, 2, …, n)为单道地震记录, m(t)(t=1, 2, …, n)为通过反馈迭代方法预测得到的该道地震记录的多次波模型, d0(t)(t=1, 2, …, n)为地震记录中的一次反射波, m0(t)(t=1, 2, …, n)为地震记录中的多次波, 其中n为时窗长度, 如果m0(t)=m(t)*a(t), *表示褶积, 即多次波模型m(t)通过自适应滤波器s(t)(t=1, 2…, l)后实际输出为地震记录中的多次波m0(t), 自适应滤波器s(t)与地震子波有关, 则有
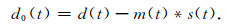
|
(1) |
按照消除多次波后的地震记录取得最小能量的准则, 自适应滤波器s(t)的求取是通过最小化(2)式的目标函数得到的:
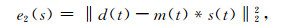
|
(2) |
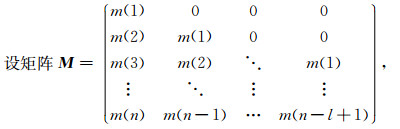
|
则(2)式向量褶积可写为矩阵乘向量形式:
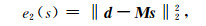
|
(3) |
(3)式对s求偏微商, 并令其等于零, 可得:
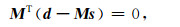
|
(4) |
式(4)相当于:
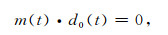
|
(5) |
即要求多次波和有效波满足正交性, 同时可以看到, 2范数最小要求去除多次波后的地震记录满足能量最小准则, 否则如果地震记录中的多次波比其附近的有效波能量弱很多的情况下, 即大值条件[25], 则消除多次波后的有效波不满足能量最小, 从而自适应滤波器S的求取不准确, 因此多次波的压制就会带来很大的误差.
2.2 单道1范数最小自适应匹配滤波单道1范数最小自适应滤波器s(t)的求取是通过最小化(6)式的目标函数得到的:

|
(6) |
(6)式的矩阵乘向量形式为
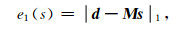
|
(7) |
目标函数e1(S)为奇异函数, 它在原点不可导.常见的优化方法比如共轭梯度法、牛顿迭代法等求目标函数的最小值都假设目标函数的一阶导数存在而且处处可导, 所以我们需要提出新的方法来求1范数的最小或者近似最小值.为此, 人们提出了许多基于线性方程的成功方法[26], 其中Huber范数被认为是一种合适的求最小值方法.本文采用的是1范数和2范数混合的迭代重加权最小平方方法[27], 该方法能够很好地进行1范数近似, 因此, 公式(7)的1范数最小化问题可以转化为下面的加权2范数最小化问题, 即:

|
(8) |
其中, W为加权矩阵: 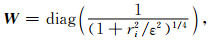


|
(9) |
其中, N是每个地震道的采样点数, 对于任意给定的ri, 可以得到:
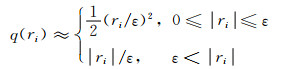
|
(10) |
从(10)式可以看出当ri比较小时, 求解的是2范数最小, 而当ri比较大时求的是1范数解, 它们的过渡点为ε.
(8)式两边对s求偏导数并令导数等于零, 则目标函数e1(S)的最小值转化为求解下式的方程组:
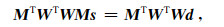
|
(11) |
矩阵MTWTWM不是Toeplitz矩阵, 所以不能用Levensin快速算法求解.对(11)式的求解, Guitton[18]采用了牛顿迭代法, 本文采用一种直接迭代的方法进行求解, 其收敛速度比较快.求解思路如下:第一步, 首先取滤波因子s为单位列向量, 即s=(1, 0, …, 0)T, 将s代人r=d-Ms得到一个r, 将得到的r代人(8)式得到一个加权矩阵W; 第二步, 将得到的W代人(11)式求解方程组可以求得一个新的s; 第三步, 将新得到的s代人r=d-Ms得到一个新的r; 第四步, 将新得到的r代人(8)式得到一个新的加权矩阵W.经过试验确定第二步至第四步只需要迭代5次就可以得到收敛的s.
(11)式变形可得:
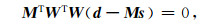
|
(12) |
式(12)相当于:
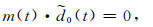
|
(13) |
其中, 
均衡多道1范数最小自适应匹配滤波是单道1范数最小自适应匹配滤波的扩展, 其目的是进一步减小对输人数据中多次波和一次波的正交性的依赖, 同时通过结合使用1范数最小和2范数最小自适应匹配滤波使得自适应滤波的求解更加准确和稳健.
设参与匹配的地震记录有k道: d1(t), d2(t), …, dk(t)(t=1, 2, …, n); 设与地震记录对应的是k道多次波模型记录为m1(t), m2(t), …, mk(t)(t=1, 2, …, n), 通过同一个自适应滤波器s(t)(t=1, 2, …, l)后实际输出为m01(t), m02(t), …, m0k(t)(t=1, 2, …, n); 去多次波后的k道一次波记录为d0 1(t), d 0 2(t), …, d 0 k(t)(t=1, 2, …, n); 则均衡多道1范数最小自适应匹配滤波方式可以表示为
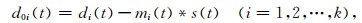
|
(14) |
(14)式写成向量乘积形式为
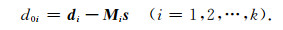
|
(15) |
自适应滤波器s(t)的求取是通过最小化下面的目标函数:
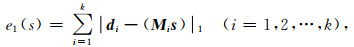
|
(16) |
与单道1范数最小自适应匹配滤波同理, 该目标函数的1范数最小化问题可以转化为下面的加权2范数最小化问题:
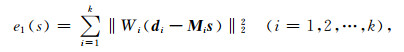
|
(17) |
其中,
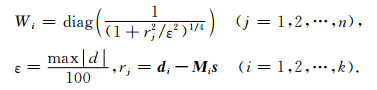
|
式(17)两边对s分别求偏微商, 并令其等于零, 则(17)式的最小化求解转化为解线性方程组:
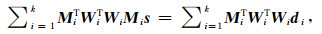
|
(18) |
方程组(18)的求解和单道1范数最小自适应匹配滤波的类似.
对(18)式变换可得:

|
(19) |
式(19)相当于:
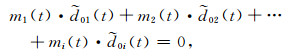
|
(20) |

下面以模型数据和野外实际数据为例, 分析单道最小二乘匹配、单道和均衡多道1范数最小匹配滤波去多次波的效果.
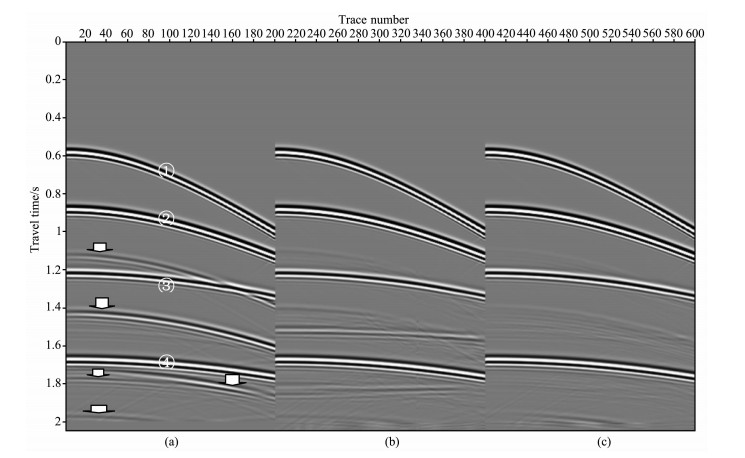
3.1 理论模型一模型一是通过有限差分正演得到的, 图 1a是其中的一个原始单炮, 同相轴①②③④为一次反射波, 箭头指示的是多次波, 图 1b是应用单道最小二乘自适应匹配滤波去多次波后的一次波记录, 图 1c是应用单道1范数最小自适应匹配滤波去多次波后的一次波记录; 图 2a是原始单炮, 图 2b是应用单道1范数最小自适应匹配滤波去多次波后的一次波记录, 图 2c是均衡多道1范数最小自适应匹配滤波去多次波后的一次波记录, 可以看到单道最小二乘匹配后存在匹配不足和过匹配的情况, 同时引人一些噪声, 而应用1范数最小自适应匹配后多次波基本上被压制掉, 同时一次波能量保持得比较好.这是因为在这个模型中一次波的能量比邻近的多次波的能量大很多, 因此不满足最小二乘自适应匹配滤波的其中一个假设条件, 而1范数最小匹配滤波则可以避免这个假设条件.
|
图 1 模型一的其中一个单炮记录及多次波压制效果对比 (a)原始单炮;(b)单道最小二乘匹配后;(c)单道1范数最小匹配后. Fig. 1 One shot profile of model 1 and the results of various multiple elimination method (a) Original shot profile; (b) By single channel least-square matching method; (c) By single channel L1-norm matching method. |

|
图 2 模型一的一个单炮记录及多次波压制效果对比 (a)原始单炮: b)单道1范数最小匹配后; (c)均衡多道1范数最小匹配后. Fig. 2 One shot profile of model 1 and the results of various multiple elimination method (a) Original shot profile; (b) By single channel L1-norm matching method; (c) By the equipoise multichannel L1-norm matching method. |
图 3a是SIGSBEE 2B模型的其中的一个原始单炮的局部放大, 箭头指示的是多次波的位置, 图 3b是应用单道最小二乘自适应匹配滤波去多次波后的一次波记录, 由于该模型比较复杂, 原始数据中存在多次波和一次波不正交的情况, 应用单道最小二乘匹配相减后衰减了部分多次波, 一次波保持得比较好, 图 3c是应用单道1范数最小自适应匹配滤波去多次波后的一次波记录, 图 3d是应用均衡多道1范数最小去多次波后的一次波记录, 可以看到经过均衡多道1范数最小匹配后多次波基本上被压制了.

|
图 3 SIGSBEE 2B模型的其中一个单炮记录及多次被压制效果对比 (a)原始单炮记录; (b)单道最小二乘匹配后; (c)单道1范数最小匹配后; (d)均衡多道1范数最小匹配后. Fig. 3 One shot profile of SIGSBEE 2B model and the results of various multiple elimination method (a) Original profile; (b) By single channel least-square matching method; (c) By single channel L1-norm matching method; (d) By the equipoise multichannel L1-norm matching method. |
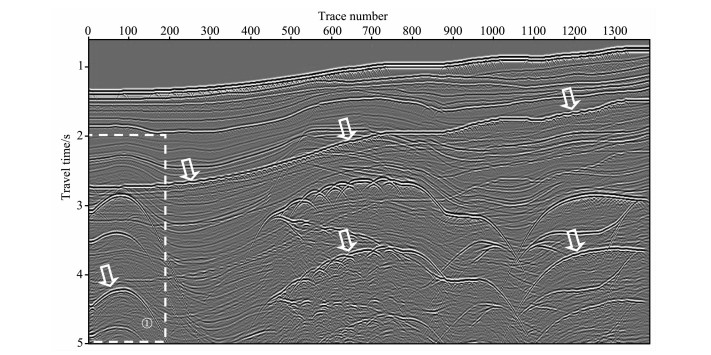
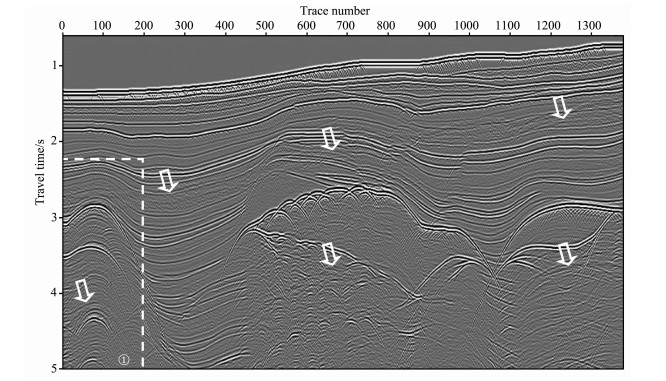
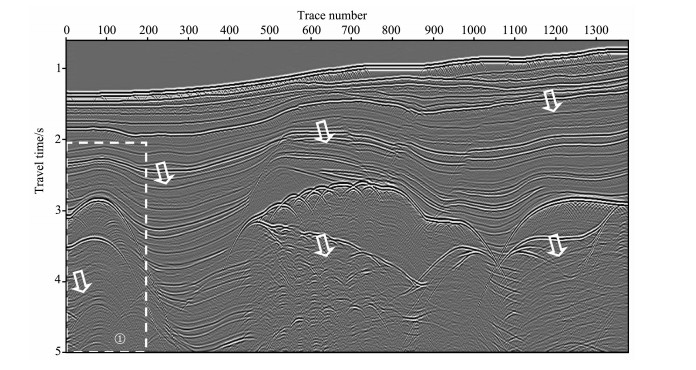
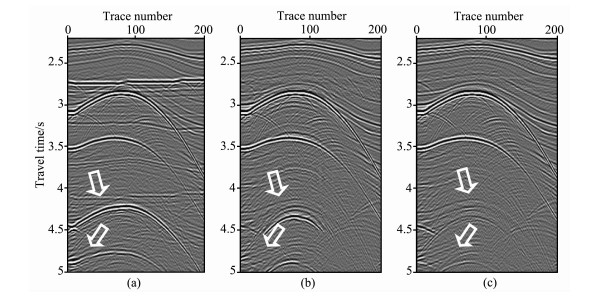
图 4是SMARRT Pluto1.5模型原始叠加剖面, 箭头指示的是多次波的位置; 图 5是单道最小二乘匹配去多次波后的叠加剖面; 图 6是均衡多道1范数最小匹配去多次波后的叠加剖面; 图 7是图 4、5、中框①的放大显示, 其中图 7a是原始记录, 图 7b是应用单道最小二乘匹配去多次波后的结果, 图 7c是应用均衡多道1范数最小匹配去多次波后的结果, 可以看到单道最小二乘匹配方法存在匹配不足或过匹配, 均衡多道1范数最小匹配多次波压制比较干净, 一次波能量保持得比较完整, 同时使得被其覆盖的一次波同相轴更加连续.
|
图 4 SMARR了模型原始叠加剖面 Fig. 4 The original stack section of SMARRT model |
|
图 5 单道最小二乘匹配去多次波后的叠加剖面 Fig. 5 The stack section after multiple elimination using single channel least-square matching filtering method |
|
图 6 均衡多道1范数最小匹配去多次波后的叠加剖面 Fig. 6 The stack section after multiple elimination using the equipoise multichannel L1-norm matching filtering method |
|
图 7 局部放大对比图 (a)原始记录; (b)单道最小二乘匹配后; (c)均衡多道1范数最小匹配后. Fig. 7 The contrast in one part of SMARRT model section (a) Original profile; (b) By singal channel least-square matching filtering method; (c) By the equipoise multichannel L1-norm matching filtering method. |
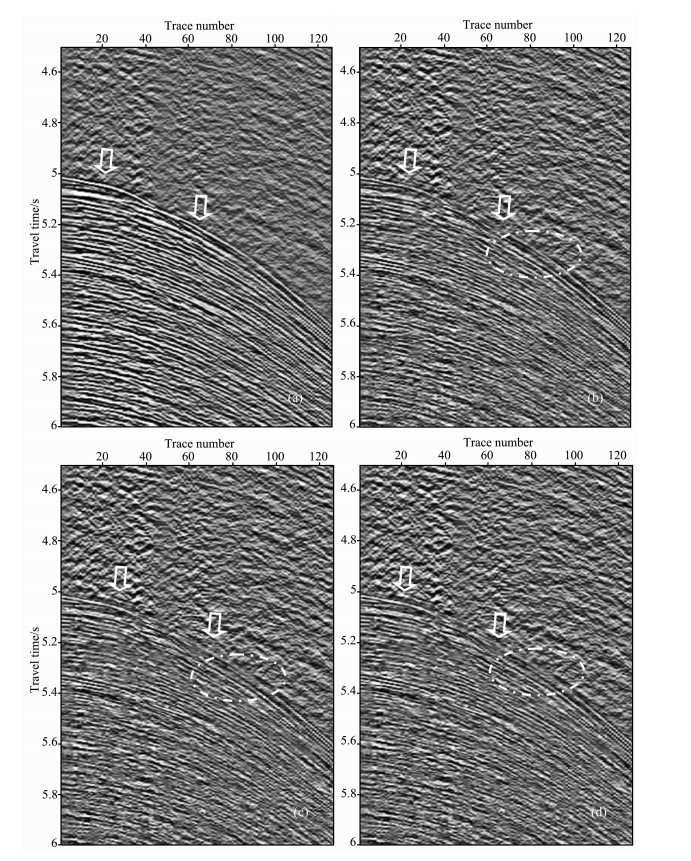
图 8是我国某海域的一个实际地震记录的原始单炮和去多次波后的效果对比, 其中图 8a是原始单炮记录, 箭头表示多次波, 图 8b是应用单道最小二乘去多次波后的单炮记录, 图 8c是应用单道1范数最小匹配去多次波后的单炮记录, 图 8d是应用均衡多道1范数最小匹配去多次波后的单炮记录; 图 9是图 8的对应虚线框部分的放大显示, 从放大图可以看到, 最小二乘匹配滤波后的多次波存在匹配不足或过匹配的情况, 因此多次波压制不是很完全, 而通过1范数匹配后的多次波衰减效果明显提高, 均衡多道1范数匹配的效果比单道1范数匹配略有改善.

|
图 8 原始单炮记录及其多次波压制效果对比 (a)原始单炮记录; (b)单道最小二乘匹配去多次波后; (c)单道1范数最小匹配去多次波后; (d)均衡多道1范数最小匹配去多次波后. Fig. 8 The original shot profile and the results of multiple elimination (a) The original shot profile; (b) The result of singal channel least-square matching filtering; (c) The result of singai L1-norm matching filtering; (d) The result of the equipoise multichannel L1-norm matching filtering. |
|
图 9 局部放大对比图 (a)原始单炮记录; (b)单道最小二乘匹配去多次波后; (c)单道1范数最小匹配去多次波后; (d)均衡多道1范数最小匹配去多次波后. Fig. 9 The constrast in part (a) The original shot profile; (b) The result of singal channel least-square matching filtering; (c) The result of singal L1-norm matching filtering; (d) The result of the equipoise multichannel L1-norm matching filtering. |
波动方程法多次波压制包括预测和相减两个步骤, 如何更好地做好相减法对多次波压制效果影响很大, 不同的匹配滤波法存在不同的假设条件, 如何处理好这些假设条件, 是多次波压制成功的关键.通过对理论模型和实际数据的多次波压制效果对比可以看到, 均衡多道1范数最小自适应匹配滤波能够较好地匹配预测的多次波模型和地震记录中的实际的多次波, 因此能更好地压制多次波, 同时保持有效波的完整性.当然该方法是假设去除多次波后的一次波不存在能量最小, 当不满足这个假设条件时, 1范数最小匹配滤波的效果和最小二乘匹配滤波的效果相同.该方法的不足之处在于它的计算量比最小二乘匹配滤波的计算量要大许多, 是其5~7倍之多, 但是由于最小二乘匹配滤波的计算速度非常快, 所以1范数最小匹配滤波的这个运算速度还是可以接受的.
| [1] | Van Dedem E J, Verschuur D J. Surface-related multiple prediction:A sparse inversion approach. Geophysics , 2005, 70: 31-43. |
| [2] | Lasse Amundsen. Elimination of free-surface related multiples without need of the source wavelet. Geophysics , 2001, 66(1): 327-341. DOI:10.1190/1.1444912 |
| [3] | 金德刚, 常旭, 刘伊克. 逆子波域消除多次波方法研究. 地球物理学报 , 2008, 51(1): 250–259. Jin D G, Chang X, Liu Y K. Research of multiple eliminationmethod in inverse wavelet domain. Chinese J.Geophys. (in Chinese) , 2008, 51(1): 250-259. |
| [4] | 刘伊克, SunH, 常旭. 基于波射线路径偏移压制多次波. 地球物理学报 , 2004, 47(4): 697–701. Liu Y K, Sun H, Chang X. Multiple removal by wavepath migration. Chinese J.Geophys. (in Chinese) , 2004, 47(4): 697-701. DOI:10.1002/cjg2.v47.4 |
| [5] | Weglein A B. Multiple attenuation:an overview of recent advances and the road ahead. Geophysics , 1999(1): 40-44. |
| [6] | Robinson E A. Predictive decomposition of seismic trace. Geophysics , 1957, 22: 767-778. DOI:10.1190/1.1438415 |
| [7] | Taner M T. Long period sea-floor multiples and their suppression. GeoPhys.Prosp. , 1980, 28: 3-48. |
| [8] | Backus M M. Water reverberation:their nature and elimination. Geophysics , 1959, 24: 23-32. |
| [9] | Foster D J, Mosher C C. Suppression of multiple reflections using the Radon transform. Geophysics , 1992, 57(3): 386-395. DOI:10.1190/1.1443253 |
| [10] | 刘喜武, 刘洪, 李幼铭. 高分辨率Radon变换方法及其在地震信号处理中的应用. 地球物理学进展 , 2004, 19(1): 8–15. Liu X W, Liu H, Li Y M. High resolution Radon transform and its application in seismic signal processing. Progress in Geophysics (in Chinese) , 2004, 19(1): 8-15. |
| [11] | 胡天跃, 王润秋, WhiteR E. 地震资料处理中的聚束滤波法. 地球物理学报 , 2000, 43(1): 105–114. Hu T Y, Wang R Q, White R E. Beamforming in seismic data processing. Chinese J.Geophys. (in Chinese) , 2000, 43(1): 105-114. |
| [12] | Yilmaz O. Seismic data processing. Society of Exploration Geophysics , 1987. |
| [13] | Wiggins J W. Attenuation of complex water-bottom multiples by wave-equatian based prediction and subtraction. Geophysics , 1988, 53(12): 1527-1539. DOI:10.1190/1.1442434 |
| [14] | Berkhout A J, Verschuur D J. Estimation of multiple scattering by iterative inversion, Part 1 Theoretical considerations. Geophysics , 1997, 62: 1586-1595. DOI:10.1190/1.1444261 |
| [15] | Weglein A B, Gasparotto F A, Carvalho P M, et al. An inverse scattering series method for attenuating multiples in seismic reflection data. Geophysics , 1997, 62: 1975-1989. DOI:10.1190/1.1444298 |
| [16] | Wang Y. Multiple subtraction using an expanded multichannel matching filter. Geophysics , 68: 346-354. DOI:10.1190/1.1543220 |
| [17] | 李鹏, 刘伊克, 常旭, 等. 均衡拟多道匹配滤波法在波动方程法压制多次波中的应用. 地球物理学报 , 2007, 50(6): 1844–1853. Li P, Liu Y K, Chang X, et al. Application of the equipoise pseudomultichannel matching filtering multiple elimination using wave equation method. Chinese J.Geophys. (in Chinese) , 2007, 50(6): 1844-1853. |
| [18] | Guitton A, Verschuur D J. Adaptive subtraction of multiples using L1-norm. Geophysical Prospecting , 2004, 52(1): 27-38. DOI:10.1046/j.1365-2478.2004.00401.x |
| [19] | 陆文凯, 骆毅, 等. 基于独立分量分析的多次波自适应相减技术. 地球物理学报 , 2004, 47(5): 886–891. Lu W K, Luo Y, et al. Adaptive multiple wave subtraction using independent compent analysis. Chinese J.Geophys. (in Chinese) , 2004, 47(5): 886-891. |
| [20] | Spitz S. Pattern recognition, spatial predictability, and subtraction of multiple events. The Leading Edge , 1999, 18(1): 55-58. DOI:10.1190/1.1438154 |
| [21] | Claerbout.Earth Sounding Analysis:Processing Versus Inversion.1992 |
| [22] | Yi Luo, Kelamis P G, Wang Y. Simultaneous inversion of multiples and primaries:inversion versus subtraction. The Leading Edge , 2003(9): 814-818. |
| [23] | Verschuur D J, Berkhout A J, Wapenaar C P A. Adaptive surface-related multiple elimination. Geophysics , 1992, 57: 1166-1177. DOI:10.1190/1.1443330 |
| [24] | Monk D J. Wave-equation multiple suppression using constrained gross-equalization. Geoghysics Prospecting , 1993, 41: 725-736. DOI:10.1111/gpr.1993.41.issue-6 |
| [25] | 李鹏.复杂介质多次波处理方法研究[博士学位论文].北京:中国科学院地质与地球物理所, 2007 Li P.The research of multiple processing method in complex media[Ph.D.thesis].Beijing:The Institute of Geology and Geophysics, Chinese Academy of Sciences, 2007 |
| [26] | Huber P J. Robust regression:Asymptotics, conjectures, and Monte Carlo. Annals of Statistics , 1973, 1: 799-821. DOI:10.1214/aos/1176342503 |
| [27] | Bube K P, Langan R T. Hybrid l1/l2 minimization with applications to tomography. Geophysics , 1997, 62: 1183-1195. DOI:10.1190/1.1444219 |
 2010, Vol. 53
2010, Vol. 53


