地震波在传播过程中会发生频散和衰减, 尤其在含油、气储层的孔隙岩石中频散和衰减往往特别明显, 因此研究波在孔隙介质中传播的机理对油、气勘探具有十分重要的意义.
根据引发机理的不同, 可以把地震波频散和衰减的原因分为外部因素和内部因素两大类.其中外部因素主要包括几何扩散、散射, 内部因素包括固体的非弹性变形, 固体之间的层面滑动和介质中的流体流动.近几十年的研究表明, 地震波在含油、气孔隙介质中传播时, 内部因素占频散和衰减的主要部分, 近期的研究又证明储层空间内由流体流动引起的耗散是内部频散和衰减的主要原因[1].
根据流动范围的大小, 孔隙介质中的流体流动又可分为宏观流体流动、微观流体流动和介观流体流动.介观尺度下的流体流动机制可以定性说明其他流动机制无法解释的重要观测现象, 引起了众多学者的注意[2~7].所谓介观尺度就是指比岩石颗粒大很多但比波长尺度小很多的中间尺度, 在岩石物理中一般指10-2~10-1m的范围.当今研究介观尺度下流体流动耗散机制的一种主要方法是基于White提出的孔隙流体部分饱和的Patchy模型. White等[2] 1975提出了含气、含水层介观交错排列的周期成层Patchy模型[2]来解释地震波在储层孔隙介质中的衰减.其后不少学者也对这种层状Patchy模型进行了相关研究[4~5, 8].同时含气、水两种孔隙流体的球状Patchy模型是White提出的另一种介观尺度下的部分饱和模型[3], Dutta等[9~11]用严格的孔隙介质力学方法研究了该模型, 并修正了White的计算公式.Caraone[5]用波动方程数值模拟的方法对中心含气的White球状Patchy模型行了研究, 发现一部分快纵波在气、水界面处转换为慢纵波, 强耗散的慢纵波再将能量衰减掉.Toms等[12]研究了空间任意排列球状Patchy模型中纵波衰减问题.众多的学者通过分析发现White提出的流体部分饱和两种Patchy模型可以定性解释地震频段下纵波频散和衰减的现象.
在过去的研究中, 我们已经用求解Bot孔隙弹性方程的方法探讨了纵波在周期成层Patchy模型中的传播特性[13], 得到了纵波速度和衰减与频率、衰减峰与渗透率、衰减峰与含气饱和度之间的关系.相对于周期成层Patchy模型, 球状Patchy模型是实际孔隙介质中两种流体饱和方式的另一种理想近似, 它也可以定性说明纵波在储层岩石中的高衰减问题.本文仍采用求解孔隙弹性方程的方法来研究纵波在球状Patchy模型中的传播.与以前的研究相比, 除了考虑纵波速度和衰减随频率的变化关系外, 本文还对地震频率下波速和含水饱和度、频散和衰减同模型空间周期的关系、频散和衰减同流体流动的关系进行了研究.
全文首先简略介绍White球状Patchy模型, 其后对模型中纵波速度及衰减的计算方法进行了阐述, 随即用数值方法对White球状Patchy模型进行了数值模拟, 并在数值求解过程中用缩减线性方程组规模的方法解决了线性方程组病态的问题, 最后对White球状Patchy模型的研究结果进行总结.
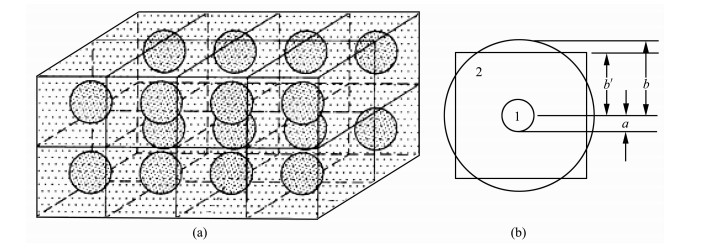
2 White球状Patchy模型简介White最初提出的空间周期排列球状Patchy模型如图 1a所示, 它由许多同时含气和水的部分饱和立方单元组成.在每个单元体中, 中心区域是气饱和孔隙介质1, 外围区域是水饱和的孔隙介质2.由于含气介质1和含水的介质2分别是一种流体饱和的孔隙介质, 所以Bot孔隙弹性理论分别适用每种孔隙介质.
|
图 1 White球状Patchy模型示意[9](a)及White球状Patchy模型征单元示意(b) Fig. 1 Schematic of White's sphere model with patchy saturation (a) and schematic of a characteristic element in White's sphere model with patchy saturation (b) |
考虑到White球状Patchy模型中孔隙介质空间周期排列的特点, 可以取示意图中任意一个空间周期内的立方体作为特征单元, 通过研究纵波在单元体中特性获知纵波在整个Patchy模型中的传播特性.为了研究的方便, White用图 1b所示的方法把单元体用一个含两种不同孔隙流体的球体来代替, 本文依旧采用这种处理方法.根据体积相等的原则等效球体半径b和立方体边长(即空间周期长度)的一半长度b'存在如下关系:
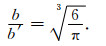
|
(1) |
由于模型几何限制, 中心球状含气孔隙介质的半径最大只能取为b', 这就决定了原始White球状Patchy模型中含气饱和度最多只能达到0.5236的临界值.在本文后面的数值计算中我们考虑了含气饱和度超过临界值的情况, 此时孔隙介质表示的是中心含水、外层含气的球状Patchy模型.
3 White球状Patchy模型中纵波速度和衰减的计算方法
当特征单元外表面受到一致简谐压力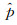
在均匀外力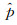
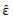
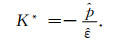
|
(2) |
在线性小应变的情况下, 方程(2)中的总体应变表示如下[9]:
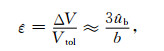
|
(3) |
ΔV是特征单元的体积变化量, Vtol是单元的总体积, ûb知表示单元外表面的固体位移.
在求得等效体积模量后, 介质中的纵波复速度可以由下式求得:
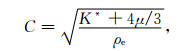
|
(4) |
其中ρe表示特征单元的等效密度, 表示形式如下:
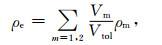
|
(5) |
上式中Vm表示单元体中孔隙介质m(m=1, 2)的体积, 孔隙介质m的密度可表示为
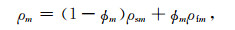
|
(6) |
其中ϕm知表示孔隙介质m中的孔隙度, ρsm, ρfm分别表示介质m中固体材料的密度和流体的密度.
取(4)式中复速度的实部可得孔隙介质中的纵波速度:
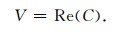
|
(7) |
纵波衰减可以采用逆品质因子来表达, 其表达形式如下[5]:
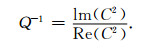
|
(8) |
White (1975年)在低频近似的前提下得出了球状Patchy模型的等效体积模量公式(附录A).本文用直接求解特征单元体中孔隙弹性方程的方法来研究纵波在球状Patchy模型中的传播, 通过引入动态频率因子的方法将低频的孔隙弹性方程扩展到高频[8].
在以特征单元中心为原点的球坐标中, 单元中含气孔隙介质1和含水介质2中的固相径向位移势可以写成如下调谐形式:
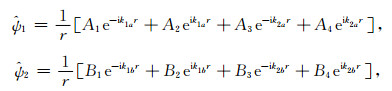
|
(9) |
其中r是径向坐标, A1, A2, A3, A4, B1, B2, B3, B4是待定系数, k1a, k2a, k1b, k2b分别代表在外力作用下孔隙介质1、2中纵波的波数.波数可以通过如下频域内孔隙介质中的波动方程获得:
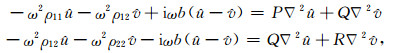
|
(10) |
其中ω表示频率, u、v分别表示孔隙介质中固相和流相的位移, i是虚数单位.质量系数ρ11、ρ12、ρ22, 弹性系数P、Q、R以及阻力系数b的求取可以参见相关文献[13, 15, 16].
由关系式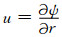
特征单元在外围一致的简谐压力作用下, 单元中只有胀缩力作用, 所以单元球心处介质的固相、液相位移为0, 即
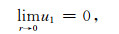
|
(11) |
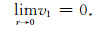
|
(12) |
下标1表示孔隙介质1中的物理量.后文中变量下标数字意义类似.
在孔隙介质1和2的分界面r=a处, 由法向总应力连续和孔隙流体压力相等有:
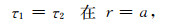
|
(13) |
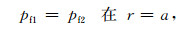
|
(14) |
其中τ表示孔隙介质中的总径向应力, pf是介质中的流体压力.
又因为在分界面处固体位移连续、流体体积流量相等, 于是:
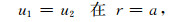
|
(15) |
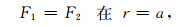
|
(16) |
其中F表示孔隙流体的相对固体骨架的流量.
在特征单元的外表面, 因为应力连续, 且无流体排出, 所以有:
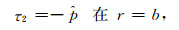
|
(17) |
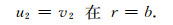
|
(18) |
通过条件(1)~(18)获得的方程组可以求得未知参数A1, A2, A3, A4, B1, B2, B3, B4, 进而由固相位移求得特征单元的变形量和体积模量.
5 数值模拟结果及分析本节主要用前面介绍的方法对中心含气, 外层含水的White球状Patchy模型(为表述方便简称为气-水Patchy模型, 后文中油-水Patchy模型意义类似)进行数值计算研究, 研究内容主要包括全频段下Patchy模型中纵波频散和衰减, 地震频段下纵波速度、衰减和含水饱和度的关系.此外还对油-水Patchy模型中纵波进行分析, 并和气-水Patchy模型中的情况进行对照研究孔隙流体流动与纵波速度和衰减的关系.在具体计算过程中通过处理将低频形式的孔隙介质方程扩展到高频段[8].
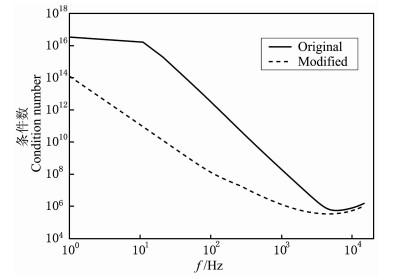
5.1 Patchy模型中纵波的频散和衰减首先在全频段下我们对气-水Patchy模型的纵波频散和衰减特性进行研究, 模型的具体材料参数见表 1.在求解过程中出现了关于A1, A2, A3, A4, B1, B2, B3, B4方程组严重病态的现象.图 2中Ongm曲线是边界条件(11)~(18)所获方程组系数矩阵在不同频率下的2范数条件数.因为条件数巨大, 如果直接求解方程将得不到正确结果.为此我们对系数矩阵进行处理.
|
|
表 1 孔隙介质的参数 Table 1 Parameters of the porous medium |
|
图 2 原方程组和处理后方程组的2范数条件数 Fig. 2 The 2-norm condition numbers of original equations and treated equations |
由条件(11)、(12)得到的具体方程如下:
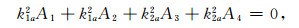
|
(19) |
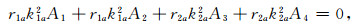
|
(20) |
对(19)、(20)式进行变形得到A1=-A2、A3=-A4, 然后将它们代人条件式(13)~(18)导出的方程组中, 得到与原8阶方程组等价的6阶新方程组. 图 2中的modfed曲线表示新方程组的条件数, 可以看到经过缩减处理, 新方程组的条件数较原方程组的明显减小, 尤其在1~1000的低频段.对于新的方程组用matlab中解线性方程组的子程序可以得到理想结果.
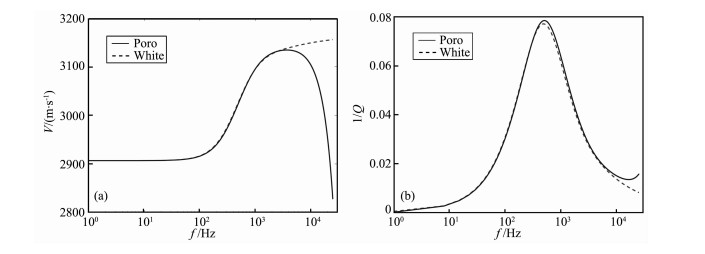
图 3a、3b是用上面数值方法得到的气-水Patchy模型中纵波的频散、衰减曲线, 图中White曲线表示用White公式得到的模型结果.Poro曲线表示用本文求解孔隙弹性方程方法得到的结果可以看到在低频段用两种方法得到的速度和衰减符合得很好, 但随着频率的升高, 两种方法的速度结果差异变得明显, 当频率超过2×104 Hz, White公式的衰减值继续下降, 而孔隙弹性力学方法得到的衰减值却开始上升.分析其原因, 对比弹性结构的声子晶体的原理[17], 由于空间的周期排列结构使得White球状Patchy模型变成了孔隙弹性的声子晶体, 当外加载荷的频率升高, 孔隙介质内的波长达到和特征单元的尺度相当时, 模型中传播的纵波进入了声子晶体的能量禁带, 所以在一定频率后出现纵波速度随频率升高而速度降低, 逆品质因子在出现第一个峰值后的一段频率后又出现衰减值增大的现象, 这和周期成层Patchy模型的结果[13]类似.由于White公式是在低频假设前提下得到的, 所以当模型内的纵波波长和特征单元尺度相当时, 低频假设已经不满足, 此时再用White方法求波速和衰减是不合理的, 而本文求解孔隙介质力学的方法可以适用于高频
|
图 3 气-水Patchy模型中纵波频散(a)及衰减(b) Fig. 3 Dispersion (a) and attemuatiom (b) of P wave in model with gas-water patchy saturation |
实际观测发现不同孔隙流体的含量对岩石中波的速度是有影响的, 为此本文对气-水Patchy模型中的纵波速度和衰减随含水饱和度的关系进行了研究.我们将特征单元的半径b保持不变, 通过改变单元中心球半径的方法达到改变气、水饱和度的效果, 当含气饱和度超过原模型允许的最大含气量0.5236时, 计算模型表示外围含气, 中间含水的球状Patchy模型.由于在实际地震勘探中, 震源的频率一般在10~100 Hz之间, 所以特征单元外围施加的简谐压力频率取为50 Hz.
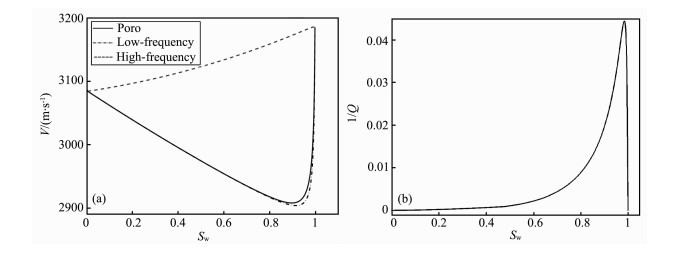
图 4a是气-水Patchy模型中纵波速度随含水饱和度(Sw)的变化情况, 其中Low-frequency曲线表示低频极限情况下用等效流体理论[18]和Gassmam理论求得的Patchy模型中纵波速度, High-frequency曲线是高频极限情况下用等效流体理论和Hill方法求得的纵波速度, 它们的具体算法可以参考附录B.从图中可以看出在指定50 Hz的低频情况下用等效流体理论求得纵波极限低频速度和用严格孔隙介质理论求得的结果差异很小.用等效流体理论和Gassmam理论估计流体Patchy饱和岩石中的纵波速度完全能够满足当前地震勘探的要求.图 4b中衰减量随含水饱和度的关系显示, 指定的地震频率下, 衰减峰值出现含水饱和度0.985附近, 其最大峰值约为0.045, 最大衰减峰值位于实际地震衰减观测值的区间内[1].此外数值结果说明在含水的孔隙流体中混入少量的气体会引起地震频段下纵波较大的衰减.
|
图 4 纵波速度(a)和衰减(b)随含水饱和度的变化 Fig. 4 Relationship between P-wave's velocity and water saturation (a) and relationship between P-wave's attenuation and water saturation (b) |
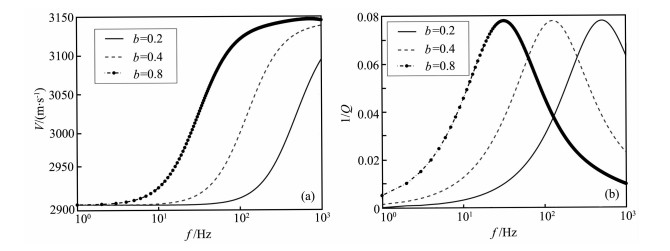
本节主要研究在孔隙流体饱和度不变的情况下, 空间周期对球状Patchy模型中纵波的影响.我们首先通过对特征单元外径调整来达到空间周期的改变, 然后根据气-水Patchy模型中含气饱和度不变(和5.1节中一样, 含气饱和度取为12.5%)的原则选取内径含气孔隙介质的半径, 再在此基础上计算不同空间周期情况下纵波的频散和衰减.
图 5a、5b分别是特征单元外径b=0.2, b=0.4, b=0.8三种情况下纵波频散和衰减曲线.从图中可以看出, 空间周期越大纵波低频部分的频散越明显; 衰减峰随着特征单元尺寸增大向低频移动, 而峰值几乎不变.
|
图 5 不同空间周期的纵波频散(a)和衰减(b) Fig. 5 P-wave's dispersion (a) and attenuation (b) with different period magnitudes in space |
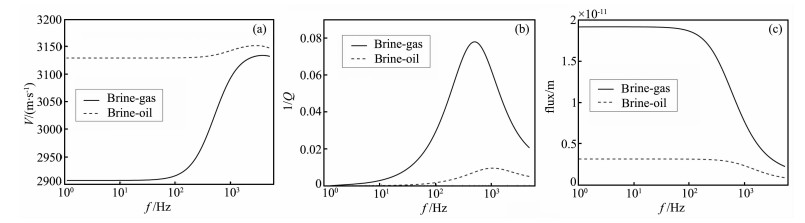
在实际的储层岩石中孔隙流体可能是气、水混合型, 也可能是油、水混合型, 甚至是油、气、水三种流体的混合.我们把前面气-水Patchy模型中的孔隙气体换为油, 用以研究油、水部分饱和情况下纵波的传播情况.在新的油-水Patchy模型中, 特征单元外层含水孔隙介质参数与前面气-水Patchy模型中的一样, 单元中心油的体积模量Ko=7×108Pa, 密度ρo=700 kg·m-3, 粘度系数ηo=1×10-3kg·m-1·s-1.
图 6(a、b、c)分别是油-水Patchy模型纵波速度、衰减和模型中两种不相混容流体交界面处流体流量.为了方便比较, 我们把气-水Patchy模型中对应的量也一同显示在图上.其中模型中的流体流量用下式来计算:
|
图 6 油-水Patchy模型中纵波速度(a)、衰减(b)及流体流量(c) Fig. 6 P-wave′s dispersion (a) and attenuation (b), and fluid flux (c) of model with oil-water saturation |
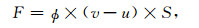
|
(21) |
S是两种孔隙流体交界面处的面积.由于含油球状Patchy模型和原来含气模型中不同孔隙流体分界面面积一样, 所以图 5c中的流体流量计算中省略掉了界面面积S, 相应流量单位变成了位移单位m (实际单位应该是m·S).
从图 6的三个图可以看出, 在两种不同的球状Patchy模型中, 在油、气含量相同的情况下, 由于油、水的体积模量的差异比油、气的差异要小, 在外界压力相同的情况下, 油、水孔隙流体之间引起的压力差比油、气孔隙流体之间的压力差要小, 从而使得油-水Patchy模型的流体流量小.又因为孔隙流体的流动影响介质的衰减和频散, 所以油-水Patchy模型中的纵波频散和衰减要比气-水Patchy模型中的小.从两种模型的频散和衰减量差异可以看出孔隙介质中的流体流动对纵波的频散和衰减影响很大.
6 结论本文在介观尺度下用孔隙介质理论对理想的White球状Patchy模型中的纵波进行研究, 发现:
(1)在低频情况下由孔隙弹性力学得到的Patchy模型纵波频散、衰减结果和White公式得到的结果符合得很好, 随着频率的升高, 波长和模型特征单元的尺寸相当时, White公式中的低频假设不再符合, 用该公式求得的结果不再合理, 而文中求解孔隙弹性力学的方法则继续适用.空间排列的周期性会使White球状Patchy模型成为孔隙弹性声子晶体这样在整个频段上模型纵波速度不会随频率单调上升, 衰减峰也不只一个.
(2)在地震低频段, 气-水Patchy模型中纵波速度和衰减随含水饱和度的变化关系表明:用等效流体理论和Gassmann理论求得的纵波低频极限速度和用严格孔隙弹性理论求得的结果差异很小, 用等效流体理论和Gassmann理论估计流体Patchy饱和岩石中的纵波速度完全能够满足当前地震勘探的要求.
(3)在保持含气饱和度不变的情况下, 随着Patchy模型空间周期尺寸的增加, 低频段的纵波频散变得明显, 纵波衰减峰频率向低频移动, 但峰值几乎不变.
(4)油-水Patchy模型和尺寸相同的气-水Patchy模型结果表明由于气、水的体积模量差异大, 在相同简谐外力作用的情况下, 气-水Patchy模型中的孔隙流体流动比油-水Patchy模型中的剧烈, 相应气-水Patchy模型中的纵波衰减和频散也较油-水Patchy模型中的大, 孔隙介质中的流体流动对纵波的频散和衰减影响很大.
本文的结论对地震勘探、声波测井资料解释和应用具有指导意义.
附录A
对于如图 1所示的球状Patchy模型, White (1975)[3]在特征单元尺度比岩石颗粒尺度大很多并比波长小很多的前提下, 假设在两种孔隙介质的交界面处流体压力不相等, 得出单元体的等效体积模量的计算公式.但是原White公式求得的纵波速度和Gassmann极限低频速度不相符的, 为此Dutta对White的公式进行了修正.后文介绍的White公式是修正后的结果.
在White公式中, 球状Patchy模型的等效体积模量可以表示成如下形式:
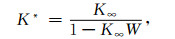
|
(A1) |
其中
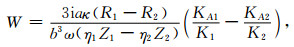
|
(A2) |
(A2)中的R1、R2表达如下:
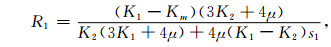
|
(A3) |
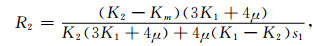
|
(A4) |
其中s1=a3/b3, 表示孔隙介质1中流体饱和度.μ是孔隙介质的剪切模量.孔隙介质1、2的阻抗表达式如下:
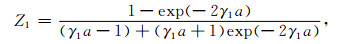
|
(A5) |
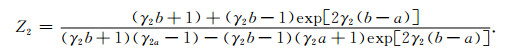
|
(A6) |
式中参数γ表达如下:
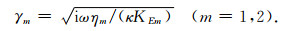
|
(A7) |
同前面提到的一样, 下标m代表图 1b中孔隙介质类型.(A7)中变量KEm、KAm表达如下:
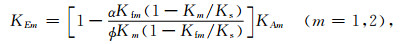
|
(A8) |
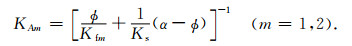
|
(A9) |
其中Biot-Willis参数表达如下:
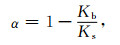
|
(A10) |
Kb表示固体骨架的体积模量, Ks是岩石颗粒的体积模量.
方程(A1)中的K∞高频极限特征单元的体积模量, 可用下式表达:
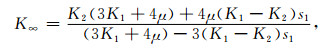
|
(A11) |
其中孔隙介质的低频的Gassmann模量K表达如下:
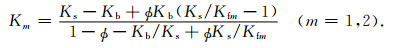
|
(A12) |
当按(A1)~(A12)得到特征单元的等效模量后, 通过式(4)、(7)、(8)求得White球状Patchy模型中纵波的速度和衰减量.
附录B
对于图 1中含有两种孔流体的孔隙介质, 在低频极限的情况下, 其等效的流体体积模量和各组分流体之间存在如下关系[18]:
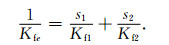
|
(B1) |
将等效流体的体积模量代人公式(B2)中求出整个White球状Patchy模型的Gassmann模量:
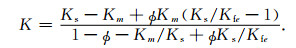
|
(B2) |
最后用模型的Gassmann模量代替(4)式中的等效体积模量K*可以求得模型中纵波的低频极限速度.
在外界作用力极其高频的情况下, 文中Patchy孔隙介质模型的体积模量可由Hill公式得到:
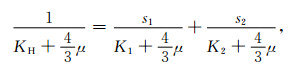
|
(B3) |
其中, KH表示高频极限时的Patchy模型的体积模量, K1、K2分别是孔隙介质1、2的Gassmann模量.在求得高频极限模量KH后, 同低频速度一样通过(4)式可以求取White球状Patchy模型中纵波的极限高频速度.
| [1] | Pride S R, Berryman J G, Harris J M. Seismic attenuation due to wave-induced flow. Journal of Geophysical Research , 2004, 109: B01201. |
| [2] | White J E, Mikhaylova N G, Lyakhovitskiy F M. Lowfrequency seismic waves in fluid-saturated layered rocks. Izvestija Academy of Sciences USSR, Physics Solid Earth , 1975, 11: 645-659. |
| [3] | White J E. Computed seismic speeds and attenuation in rocks with partial gas saturation. Geophysics , 1975, 40: 224-232. DOI:10.1190/1.1440520 |
| [4] | Gurevich B, Lopatnikov S L. Velocity and attenuation of elastic waves in finely layered porous rocks. Geophysical Journal International , 1995, 121: 933-947. DOI:10.1111/gji.1995.121.issue-3 |
| [5] | Carcione J M, Helle H B, Pham N H. White's model for wave propagation in partially saturated rocks:Comparison with poroelastic numerical experiments. Geophysics , 2003, 68: 1389-1398. DOI:10.1190/1.1598132 |
| [6] | Caraone J M, Picotti S. P-wave seismic attenuation by slowwave diffusion:Effects of inhomogeneous rock properties. Geophysics , 2006, 71: 1-8. |
| [7] | 巴晶.复杂孔隙介质中地震波传播研究[博士论文].北京:清华大学航天航空学院, 2008 Ba J.Research on the seismic wave propagation in complex porous media[Ph.D.thesis](in Chinese).Beijing:School of Aerospace of Tsinghua University, 2008 |
| [8] | Vogelaar B, Smeulders D. Extension of White' s layered model to the full frequency range. Geophysical Prospecting , 2007, 55: 685-695. DOI:10.1111/gpr.2007.55.issue-5 |
| [9] | Dutta N C, Ode H. Attenuation and dispersion of compressional waves in fluid-filled porous rocks with partial gas saturation (White model)-Part I:Biot theory. Geophysics , 1979, 44: 1777-1788. DOI:10.1190/1.1440938 |
| [10] | Dutta N C, Ode H. Attenuation and dispersion of compressional waves in fluid-filled porous rocks with partial gas saturation (White model)-Part II:Results. Geophysics , 1979, 44: 1789-1805. DOI:10.1190/1.1440939 |
| [11] | Dutta N C, Seriff A J. On White's model of attenuation in rocks with partial saturation. Geophysics , 1979, 44: 1806-1812. DOI:10.1190/1.1440940 |
| [12] | Toms J, Muller T M, Gurevich B. Seismic attenuation in porous rocks with random patchy saturation. Geophysical Prospecting , 2007, 55: 671-678. DOI:10.1111/gpr.2007.55.issue-5 |
| [13] | 刘炯, 马坚伟, 杨慧珠. 周期成层Patchy模型中纵波的频散和衰减研究. 地球物理学报 , 2009, 52(11): 2879–2885. Liu J, Ma J W, Yang H Z. Research on dispersion and attenuation of P wave in periodic layered-model with patchy saturation. Chinese J.GeoPhys. (in Chinese) , 2009, 52(11): 2879-2885. DOI:10.3969/j.issn.001-5733.2009.11.023 |
| [14] | Mavko G, Mukerji T, Dvorikin J. The Rock Physics Handbook:Tools for Seismic Analysis in Porous Media. London: Cambridge University Press, 1998 . |
| [15] | Biot M A. Theory of propagation of elastic waves in a fluidsaturated porous solid:I. Low frequency range.Journal of the Acoustical Society of America , 1956, 28: 168-178. DOI:10.1121/1.1908239 |
| [16] | Geertma J. The effect of fluid pressure decline on volumetric changes of porous rocks. Petroleum Trans.AIME , 1957, 210: 169-181. |
| [17] | 温熙森. 光子/声子晶体理论与技术. 北京: 科学出版社, 2006 . Wen X S. The Theory and Technology of Photonic and Phononic Crystal (in Chinese). Beijing: Science Press, 2006 . |
| [18] | Sengupta M, Mavko G. Impact of flow-simulation parameters on saturation scales and seismic velocity. Geophysics , 2003, 68: 1267-1280. DOI:10.1190/1.1598119 |
 2010, Vol. 53
2010, Vol. 53



