2. 中国科学院研究生院, 北京 100049
2. Graduate University of Chinese Academy of Sciences, Beijing 100049, China
地球主磁场的极性、强度、方向、能量和空间分布经历着系统而缓慢的变化,即长期变化(Secular Variation,简称SV)[1~4].主磁场(B)及其时间变化场(Ḃ)均起源于地球外核的磁流体发电机过程[5].
现代地磁观测开始于1837年,历史观测也可以追溯到1590年.这些资料广泛运用于研究短周期的长期变化,如十年到百年尺度的变化[6, 7].在分析地磁场长期变化规律时,许多研究者[8~13]多次报道了“60年周期”的存在,它与日长变化的关系也受到广泛关注.Yokoyama和Yukutake[11],以及康国发等[14]的研究认为这一周期与日长十年尺度波动存在一定的相关性.利用地面台站资料还发现了所谓的“地磁急变”(jerk),也就是长期变化脉冲[15~17].通过卫星观测,这一现象也得到了进一步证实[18~21].从20世纪到现在,1901、1913、1925、1969、1978、1991年和2003年曾经出现过几次全球范围内的急变现象.这几次显著变化大约间隔10~12年发生一次,每次持续时间1~2年.此外,全球地面台站某些地磁分量长期变化中也存在10年以下的周期[22].
古地磁、考古地磁记录的谱分析中可以得到地质年代的周期成分,时间尺度从百年到百万年不等[23, 24].ConstableC和ConstableS [25, 26]给出的地磁场总谱(振幅谱)描述了占优势的各种时间尺度的周期变化现象.其中,反映地核流体运动的内源变化在长周期部分占优势,如偶极子磁极倒转,时间尺度为105到106年;此外,还包括外源磁场的变化周期,主要有11年太阳黑子周、年和半年变化、太阳旋转的27天变化、逐日变化、几秒到几小时段的磁暴活动以及静日变化等.上述周期变化的研究已经比较完善,而有关长期变化几十年到千年尺度的周期研究还较少.因此,研究主磁场十年到百年尺度的长期变化有助于丰富地磁场总谱的内容.此外,这一周期尺度与人类的寿命长度相当,并且地磁长期变化还可能与全球变化和十年到百年尺度的气候变化有紧密联系[27],所以更值得人们关注.
虽然人们已经做了许多工作研究短周期的长期变化,但十年到百年尺度的周期研究仍然存在不少问题.就观测手段而言,现代地磁观测属于直接观测,古地磁、考古地磁属于间接观测.由于测年技术的精度问题,古地磁、考古地磁资料所取的时间间隔往往超过几十年,甚至长达上百年,这样的精度不足以得到较短周期(小于数百年)的变化.另一方面,因为系统的全球地磁观测到现在仅有175年的历史,几乎没有几个台站能得到如此长期的、连续的、超过百年以上的记录.所以现代地磁观测数据的时间跨度还太短,不足以得到数十年左右的周期.
以往的长期变化研究中,既可以使用实际的观测数据做分析,也可以通过已有的模型去反演地磁场的时间和空间变化,选择何种方法取决于研究问题的出发点.因为原始观测资料中很难完全去除所有外源场的影响,在研究长期变化周期时会影响谱分析结果的准确性.而使用主磁场模型时,通常假定外源场的影响已经在模型建模过程中去除了,所有变化都来自内源场.本研究中使用Jackson等[7]给出的历史地磁场模型gufm1,该模型的资料来源于直接的地磁观测,可以追溯到16世纪第一个定量记录,时间跨度长达四百年,有利于研究十年到百年尺度的周期变化.
小波分析方法具有很好的时频定位特性,有利于获取非稳态信号的局部特征.本文主要应用小波变换技术分析了gufm1模型高斯系数的长期变化,以及由模型推导出的多个参数,如磁极强度(无符号磁通量)、能谱等随时间的变化.因为地表处的磁场低阶球谐分量占优势,所以本文在计算过程中能谱的最高阶数取到3阶.其他参数的偶极子部分取n=1的项,非偶极子部分取n≥2的项.
2 资料预处理主磁场B本身的长期变化主要由三个部分组成,即常数项、线性项以及某些周期项的级数和.研究长期变化Ḃ场可以消除常数项和线性趋势对B场谱分析的影响.这样常数项变为零,线性项变为常数项,不但不会对周期大小的估计产生本质上的影响,而且周期项的变化更加明显.
为了分析主磁场的长期变化,需要有足够长的时间序列.虽然国际地磁参考场IGRF(International Geomagnetic Reference Field)模型被广泛用于地球深部、地壳、电离层和磁层等地磁场各方面的研究[28~32],但是这种模型的时间跨度只有110多年,不足以提取长期变化中世纪尺度的周期分量.根据Bloxham和Jackson[6]1992年得到的ufm模型(包括ufm1和ufm2模型,其中ufm2时间跨度为1690~1840年;ufm1为1840~1990年),Jackson等[7]又于2000年提出了gufm1模型.该模型时间跨度往前推进了100年,包含1590~1990年近400年的模型系数,便于研究主磁场十年到百年尺度的长期变化.该模型还可以从地表直接下延到核幔界面,且精度大大提高,时间分辨率达到2.5年.此外,Finlay等[33]已经得到了最新的gufm系列模型的初步结果,将可以提供长达415年的主磁场模型.需要指出的是,1832年高斯(Gauss)发明地磁场绝对强度的测量方法之前,地磁场只有方向观测(磁偏角和磁倾角),没有绝对强度测量值.gufm1模型中最大的ġ10项1840年以前的系数只能通过15nT/a的变化率线性外推得到[7],所以本文研究中主要关注gufm1模型1840年以后的资料,时间跨度长达150年,而整个400年的资料可用作参考.
3 分析方法 3.1 小波变换小波变换是一种分析非稳态信号的有效工具,在地球物理学和地磁学等各项研究中得到了广泛运用[13~16, 34~36].谱分析方法如短时傅里叶变换[37]、最大熵谱分析[10]、经验模式分解[12]等,已经在很大程度上改进了对周期大小的估计.但是这些方法只能告诉我们存在些什么周期,却不能确定这些周期什么时候出现.小波分析可以对周期分量进行时间定位.传统的傅里叶分析只能给出诸如T/n(n=1,2,…,i)的离散周期谱线,而小波分析可以分别提取出各个谐波分量.比如说,在傅里叶谱中出现两个相邻的峰,我们并不能断定这是两个谐波还是一个变化的谐波.这一信息对研究周期的动态变化很有意义.
根据Torrence和Compo[38]的方法,有限时间系列f(t)的小波变换可以表示成积分的形式,
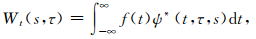
|
(1) |
其中,*表示复数的共轭,尺度s是伸缩因子,τ是平移参数,Wt(s,τ)表示小波系数. 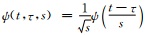
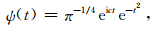
|
(2) |
式中,c为无维度的频率.为满足容许性条件(admissibility condition),这里将c的值取为6[39]. ψ(t)和Wt(s,τ)是复数,可以分解为实部和虚部,或振幅和相位.通常用振幅的平方|Wt(s,τ)|2绘制小波能谱图,但是这种做法只能给出单个的宽的谱峰,并不容易识别确切的周期值.实际上,可以用小波系数的实部或虚部分别绘制小波能谱图,则时间系列的波动可以分离成正的峰和负的谷,这样就能更好地表示各个准周期分量的动态变化.同时定义全局小波能谱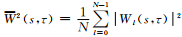
Bondi和Gold[40]定义了“无符号磁通量”(Unsigned magnetic flux)或“磁极强度”(Pole-strength),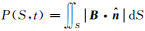

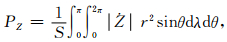
|
(3) |
式中,θ和λ分别是余纬和经度,r是地心距(地表处取地球的平均半径r=6371.2km),S是地球表面积,Ż是垂直分量Z的一阶导数.
为考察多极子的相对贡献,根据Lowes谱[41]的表达式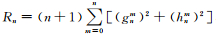
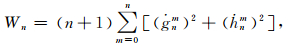
|
(4) |
式中,ġnm、ḣnm分别是高斯系数gnm和hnm的一阶时间导数.这里需要指出的是,Wn反映的是Ḃ场偶极子和多极子的相对重要性,而不是真正的Rn的能量变化率(即Rn对时间的一阶导数).
偶极子磁矩可以用n=1的三个高斯系数g10、g11和h11来表示.它随时间的变化表示成
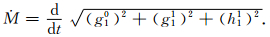
|
(5) |
除了上述三个参数外,本文还将分析gufm1模型高斯系数的变化率.此外,无符号磁通量是一种全球平均量,描述的是全球磁场的总体特征,其他三个参数只给出地磁场某一方面的信息.如,偶极子磁矩反映的是偶极子场的信息,能谱反映各阶多极子的相对贡献,而单个高斯系数反映的是某一阶谐波的变化.
4 结果
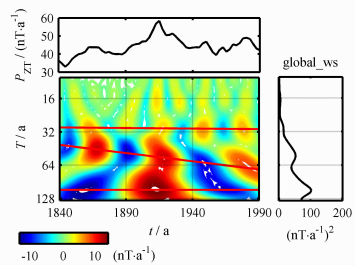
图 1给出总磁极强度PZT的小波图(左下图).最上面一幅图是用来做小波分析的总磁极强度的时间系列,右下图中的曲线表示全局小波能谱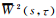
|
图 1 总磁极强度Pzt小波图 上图是用来做小波分析的总场时间系列,左下图是小波能谱,t表示时间,T表示周期.右下方图中的曲线表示全局小波能谱,代表周期的强度. Fig. 1 Wavelet power spectrum of the totil pole-strength PZT The upper panel is the time series of the total field used for the wavelet analysis. The lower lett panel is its wavelet spectrum, in which t is time, T represents theperiod. The curve in the right panel s the global wavelet spectrum, which represents the strength of periods. |
(1)30年周期:图 1中,从1840年到1990年,150年间存在五对焦点中心,平均周期约为30年.这一周期的强度和大小都随时间发生一定变化,但是变化不显著,显示出稳定的周期性.
(2)准50年周期:从图 1中还可以发现一个频散的周期分量.这一周期从1840年的40年周期变为1990年的69年周期,三对等值线焦点中心说明这一分量的平均周期约为50年.
(3)110年周期:除了上述两个十年尺度的周期分量,还可以看出存在一个110年左右的世纪周期,由一个红色和两个蓝色的焦点中心来表示.在本文分析的时间段内,它的周期大小没有显著的变化,但是强度会发生变化.
右下图给出了对应的全局能谱,三个峰分别对应三个主要的周期分量.可以看出,30年的周期变化强度最小,而110年周期最大,50年周期次之.主要是因为小波变换得到的小波系数中各周期变化的幅度不同,且周期大小随时间动态变化.全局能谱表示的是各个周期的平均结果.
研究中发现,总场的能谱主要是由偶极子和非偶极子贡献的.下面将分别讨论偶极子和非偶极子的小波能谱,探寻影响这些主要周期分量的因素.
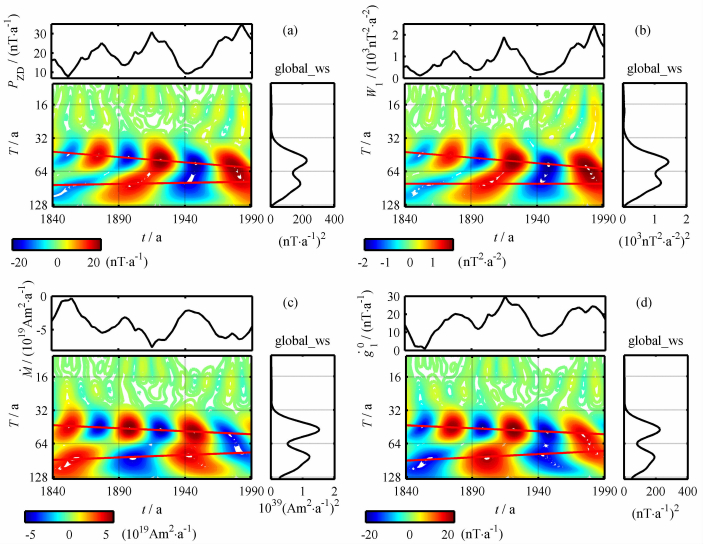
4.1 偶极子场图 2(a~c)分别给出偶极子磁极强度PZD、偶极子能谱W1以及偶极子磁矩Ṁ的小波能谱.这三个量与图 2d中高斯系数ġ10显示出相似的长期变化和能谱结构,说明它们依赖于ġ10的变化.不同的是,图 2c中磁矩Ṁ的变化与其他三个参数反相.可以看出,最上面一条粗红线连接的三对焦点中心显示出清楚的准50年周期,并且存在一定程度的发散.此外,从图 2(a~d)中还可以看出存在80年左右的周期,周期大小随时间减小.因此可以得出结论,这一频散的准50年周期至少有一部分是由偶极子场产生的.
|
图 2 偶极子场的小波能谱 (a)磁极强度Pzd (b)能谱W1; (c)偶极子磁矩Ṁ; (d)高斯系数ġ10. Fig. 2 Wavelet power spectrum of the dipole field (a) Pole-strength PZd; (b) Power spectrum W1; (c) Dipole moment Ṁ (d) Gauss coefficient ġ10 |
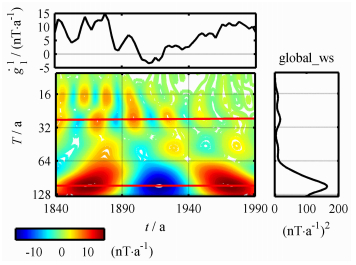
偶极子场主要是由轴向偶极子分量ġ10贡献的,赤道分量ġ11也有贡献,如图 3所示.从图中可以看出,最上面一条红线连接的焦点中心显示出稳定的30年周期,它的全局能谱表示的周期强度并不大.最下面的红线趋势表示的是110年左右的周期,全局能谱的强度也是最强的.此外,全局能谱中似乎还有两个强度非常微小的变化,但是相应的等值线焦点中心在整个时段内不是都连续,在此暂不讨论.
|
图 3 高斯系数ġ11的小波能谱 Fig. 3 Wavelet power spectrum of the Gauss coefficient ġ10 |
以上分析表明,偶极子场的轴向分量对准50年的周期贡献最大,而赤道分量对30年和110年周期贡献较大.
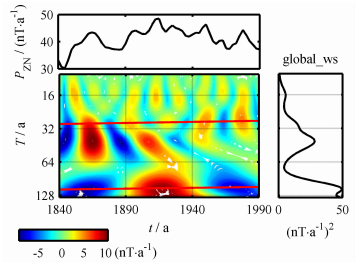
4.2 非偶极子场图 4给出非偶极子磁极强度PZN的小波能谱.可以看出,比较连续的周期变化有两个:一个是110年左右的显著周期,对应的全局能谱也是最强的,表明非偶极子场对世纪分量贡献显著.此外,还有一个30年左右的周期.
|
图 4 非偶极子磁极强度PzN的小波能谱 Fig. 4 Wavelet power spectrum of the non-dipole pole-strength PZN |
为了更加详细地考察这些周期分量的来源,本文进一步分析了四极子和八极子场的周期特征,这也是组成非偶极子场最重要的两个部分.
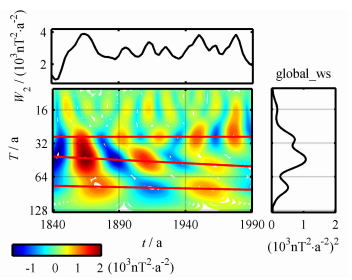
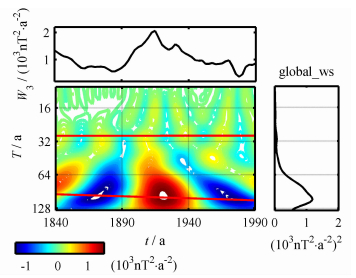
图 5给出了四极子场W2的小波能谱.首先,存在一个30年左右的周期,这一点与图 4类似.不同的是,图 5中还有一个逐渐增大并发生频散的准50年周期,以及一个比较弱的80年左右的周期.图 6是八极子场的小波图,和图 3中的赤道分量ġ11以及图 4中的非偶极子磁极强度PZN类似,存在30年和110年左右的周期.
|
图 5 四极子能谱W2的小波能谱 Fig. 5 Wavelet power spectrum of the quadruple power spectrum W2 |
|
图 6 八极子能谱W3的小波能谱 Fig. 6 Wavelet power spectrum of the octupole power spectrum W3 |
上述分析表明,四极子场对30年和50年周期起主要作用,而八极子场对30年和110年周期均有贡献.
5 讨论本文的分析表明,地磁场长期变化存在显著的周期变化,时间尺度从几十年到上百年.根据磁极强度,本文分析了偶极子和非偶极子场的多个参数,探寻不同周期分量的来源.从偶极子和非偶极子场的小波图中均可以看到相似的长期变化谱结构,表明多种成分对这些周期分量有贡献.
可以预期的是,不同的数据和分析方法会得到不同的结果.Roberts等[12]应用经验模式分解方法分析了10个地磁台站的磁偏角和倾角资料,得到了60年的显著周期,此外还得到30年的次显著周期.他们的研究将台站记录分为1840年之前(资料质量较差)和1850年之后的时段分别进行分析.本文主要分析gufm1模型1840年以后的资料,这样得到的结果才更加可靠.因为主磁场长期变化的频率比较低(周期长),而本文所使用的资料每2.5年一个,并且总的时间长度是150年,所以能得到的周期范围在5~150年之间.作为参考,本文还同时利用整个400年的资料分析了磁极强度、能谱及高斯系数等地磁参数的长期变化.结果证明,除几十年的周期分量以外,不同的参数还可以得到多个百年以上的周期.如高斯系数变化率ġ21的122年周期、偶极子磁极强度PZD的133年和139年周期、总磁极强度PZT的158年周期,以及八极子能谱W3的165年周期等.但是因为1837年以前缺乏绝对强度的观测,所以这些周期的可靠性还有待进一步的研究证实.
以上分析表明,长期变化的周期结构非常复杂,各周期分量的强度和大小都会随时间变化.在本文的研究中,频散是长期变化中常见的一个现象,如图 1和图 2所示.某些时段单个的周期分裂成两个周期,或者两个周期逐渐合并成一个周期.这样,定义某一时段内的平均周期会因发生频散而引起误解.因此,有必要引入动态谱分析(如小波分析).
需要指出的是,引起地磁场长期变化周期性变化的原因非常复杂.究其原因,可能还是和产生地磁场的地核发电机过程密不可分,并且不同大小的周期变化反映了核幔边界和地核表面不同尺度的流体运动.至于何种方式起作用目前还不是很清楚.一种可能的解释认为与环型振荡(Torsional oscillation)有关[42, 43].Dickey和de Viron[43]最近的工作表明,环型振荡可以从核幔边界传播到内核,周期分别为85、50、35年和28年.这些结果与本文得到的除110年以外的其他两个周期,即30年和50年左右的周期符合得比较好,也与现代地磁观测的结果比较一致.而110年的周期似乎存在争议,因为很少有台站记录能超过这个时间长度.但是借助小波的方法确实能从近150年的资料中分析出这一周期.进一步有力的证据有待于更多高精度的观测记录的增加和先进的分析方法的出现来给出.
简而言之,通过研究历史地磁场资料有利于丰富地磁总谱几十年到百年尺度的周期信息.如果联合考古地磁和古地磁资料,可以得到地磁场长期变化几十年到上千年连续的谱.
6 结论本文分析了地磁场长期变化十年到百年尺度的周期变化,主要得到了三个周期:稳定的30年周期、频散的准50年周期和强度变化的110年周期. 30年的周期主要是在偶极子场的赤道分量ġ11,以及非偶极子场中较常见.准50年的周期主要由轴向偶极子分量ġ10贡献的,四极子场能谱W2也有贡献.而110年的周期来源于偶极子场的赤道分量、非偶极子场磁极强度PZN以及八极子场能谱W3.
致谢感谢美国NASA哥达德航天中心(NASA Goddard Space Flight Center)匡伟佳教授有益的讨论.本文使用的程序改编自C.Torrence和G.Campo的小波程序(http://paos.colorado.edu/research/wavelets).
| [1] | 徐文耀, HenriClaudNataf, 魏自刚, 杜爱民. 地磁场长期变化速率的30年周期. 地球物理学报 , 2006, 49(5): 1329–1338. Xu W Y, Nataf H C, Wei Z G, Du A M. Thirty-year period in secular variation rate of the main geomagnetic field. Chinese J.Geophys. (in Chinese) , 2006, 49(5): 1329-1338. |
| [2] | 徐文耀, 白春华. 非洲磁异常对地磁场结构及其长期变化的控制作用. 地球物理学报 , 2009, 52(8): 1985–1992. Xu W Y, Bai C H. Role of the African magnetic anomaly in controlling the magnetic configuration and its secular variation. Chinese J.Geophys. (in Chinese) , 2009, 52(8): 1985-1992. |
| [3] | 康国发, 吴小平, 文丽敏, 等. 地球主磁场的能量密度谱及其长期变化. 地球物理学进展 , 2003, 18(1): 111–115. Kang G F, Wu X P, Wen L M, et al. The energy density spectrum and secular variation of the Earth's main magnetic field. Progress in Geophysics (in Chinese) , 2003, 18(1): 111-115. |
| [4] | 康国发, 白春华, 李伟, 等. 1690-2000年地磁场能量的三维分布及长期变化. 地球物理学进展 , 2007, 22(1): 80–86. Kang G F, Bai C H, Li W, et al. Three-dimensional distribution of geomagnetic energy in the Earth' s interior and its secular variation for 1690-2000a. Progress in Geophysics (in Chinese) , 2007, 22(1): 80-86. |
| [5] | Le Mouel J L. Outer-core geostrophic flow and secular variation of Earth's geomagnetic field. Nature , 1984, 311(5988): 734-735. DOI:10.1038/311734a0 |
| [6] | Bloxham J, Jackson A. Time-dependent mapping of the magnetic field at the core-mantle boundary. J.Geophys.Res. , 1992, 97(B13): 19537-19563. DOI:10.1029/92JB01591 |
| [7] | Jackson A, Jonkers A R T, Walker M R. Four centuries of geomagnetic secular variation from historical records. Philos.Trans.R.Soc.London, Ser.A , 2000, 358(1768): 957-990. DOI:10.1098/rsta.2000.0569 |
| [8] | Braginsky S I. Short-period geomagnetic secular variation. Geophys.Astrophys.Fluid Dynam. , 1984, 30(1): 1-78. |
| [9] | Langel R A, Kerridge D J, Barraclough D R, Malin S R C. Geomagnetic temporal change:1903-1982, A spline representation. J.Geomagn.Geoelectr. , 1986, 38(6): 573-597. DOI:10.5636/jgg.38.573 |
| [10] | Jin R-S, Jin S. The~60-year power spectral peak of the magnetic variations around London and the Earth' s rotation rate fluctuations. J.GeoPhys.Res. , 1989, 94(B10): 13673-13679. DOI:10.1029/JB094iB10p13673 |
| [11] | Yokoyama Y, Yukutake T. The 60-year variation in the rate of rotation of the Earth and the geomagnetic field. J.Geomagn.Geoelectr. , 1992, 44(7): 555-560. DOI:10.5636/jgg.44.555 |
| [12] | Roberts P H, Yu Z J, Russell C T. On the 60-year signal from the core. Geophys.Astrophys.Fluid Dynam. , 2007, 101(1): 11-35. DOI:10.1080/03091920601083820 |
| [13] | Ivanov V V, Bondar T N. Wavelet analysis of temporal and spatial parameters of the 60-year variation in the geomagnetic field. Geomag.Aeron. , 2008, 48(5): 680-688. DOI:10.1134/S0016793208050125 |
| [14] | 康国发, 白春华, 高国明. 地磁场长期变化和日长十年尺度变化的周期特征. 地球物理学报 , 2008, 51(2): 369–375. Kang G F, Bai C H, Gao G M. Periodical characteristics of the geomagnetic secular variation and length-of-day variation. Chinese J.Geophys. (in Chinese) , 2008, 51(2): 369-375. |
| [15] | Alexandrescu M, Gibert D, Hulot G, et al. Detection of geomagnetic jerks using wavelet analysis. J.Geophys.Res. , 1995, 100(B7): 12557-12572. DOI:10.1029/95JB00314 |
| [16] | Alexandrescu M, Gibert D, Hulot G, et al. Worldwide wavelet analysis of geomagnetic jerks. J.Geophys.Res. , 1996, 101(B1O): 21975-21994. |
| [17] | Macmillan S. A geomagnetic jerk for the early 1990's. Earth Planet.Sci.Lett. , 1996, 137(1-4): 189-192. DOI:10.1016/0012-821X(95)00214-W |
| [18] | Wardinski I, Holme R.Decadal and subdecadal secular variation of main geomagnetic field.In:Reigber C, Luhr H, Schwintzer P eds.First CHAMP Mission Results for Gravity, Magnetic and Atmospheric Studies (2002).Berlin:Springer, 2003.226~232 |
| [19] | Mandea M, Olsen N. A new approach to directly determine the secular variation from magnetic satellite observations. Geophys.Res.Lett. , 2006, 33: L15306. DOI:10.1029/2006GL026616 |
| [20] | Olsen N, Mandea M. Investigation of a secular variation impulse using satellite data:The 2003 geomagnetic jerk. Earth Planet.Sci.Lett. , 2007, 255(1-2): 94-105. DOI:10.1016/j.epsl.2006.12.008 |
| [21] | Wardinski I, Holme R, Asari S, Mandea M. The 2003geomagnetic jerk and its relation to the core surface flows. Earth Planet.Sci.Lett. , 2008, 267(3-4): 468-481. DOI:10.1016/j.epsl.2007.12.008 |
| [22] | Ladynin A V, Popova A A. Quasi-periodic geomagnetic secular variation (from 1985-2005 world observatory data). Russ.Geol.Geophys. , 2008, 49(12): 951-962. DOI:10.1016/j.rgg.2008.04.006 |
| [23] | Hongre L, Hulot G, Khokhlov A. An analysis of the geomagnetic field over the past 2000 years. Phys.Earth Planet.Int. , 1998, 106(3-4): 311-335. DOI:10.1016/S0031-9201(97)00115-5 |
| [24] | Korte M, Constable C G. Centennial to millennial geomagnetic secular variation. Geophys.J.Int. , 2006, 167(1): 43-52. DOI:10.1111/gji.2006.167.issue-1 |
| [25] | Constable C G, Constable S C.Satellite magnetic field measurements:applications in studying the deep Earth.In:Sparks R S J, Hawkesworth C J eds.State of the Planet:Frontiers and Challenges in Geophysics.Washington, D.C.:American Geophysical Union, 2004.147-159 |
| [26] | Constable C.Geomagnetic spectrum, temporal.In:Gubbins D, Herrero-Bervera E eds.Encyclopedia of Geomagnetism and Paleomagnetism.Dordrecht:Springer Netherlands, 2007.353~355 |
| [27] | Gallet Y, Genevey A, Fluteau F. Does Earth's magnetic field secular variation control centennial climate change? Earth Planet. Sci.Lett. , 2005, 236(1-2): 339-347. |
| [28] | 徐文耀. 国际参考地磁场模型中高阶球谐项对地磁场长期变化的影响. 地球物理学报 , 2003, 46(4): 476–481. Xu W Y. Effect of high-degree harmonics in the IGRF models on secular variation of the geomagnetic field. Chinese J.Geophys. (in Chinese) , 2003, 46(4): 476-481. |
| [29] | 徐文耀. 地磁场的三维巡测和综合建模. 地球物理学进展 , 2007, 22(4): 1035–1039. Xu W Y. Three dimensional survey and comprehensive modeling of geomagnetic field. Progress in Geophysics (in Chinese) , 2007, 22(4): 1035-1039. |
| [30] | 徐文耀, 杜爱民, 白春华. 地球磁层的磁场模型. 地球物理学进展 , 2008, 23(1): 14–24. Xu W Y, Du A M, Bai C H. Magnetic field models of the Earth' s magnetosphere. Progress in GeoPhysics (in Chinese) , 2008, 23(1): 14-24. |
| [31] | 徐文耀, 白春华, 康国发. 地壳磁异常的全球模型. 地球物理学进展 , 2008, 23(3): 641–651. Xu W Y, Bai C H, Kang G F. Global models of the Earth's crust magnetic anomalies. Progress in Geophysics (in Chinese) , 2008, 23(3): 641-651. |
| [32] | 白春华, 徐文耀, 康国发. 地球主磁场模型. 地球物理学进展 , 2008, 23(4): 1045–1057. Bai C H, Xu W Y, Kang G F. Main geomagnetic field models. Progress in Geophysics (in Chinese) , 2008, 23(4): 1045-1057. |
| [33] | Finlay C C, Jackson A, Gillet N.Progress towards a new historical field model.AGU Fall Meeting Abstracts, 2006 |
| [34] | Kumar P, FoufoulaGeorgiou E. Wavelet analysis for geophysical applications. Rev.Geophys. , 1997, 35(4): 385-412. DOI:10.1029/97RG00427 |
| [35] | 乐贵明, 王家龙. 太阳黑子相对数最强周期的小波分析. 地球物理学报 , 2004, 47(5): 743–746. Le G M, Wang J L. Wavelet analysis of the strongest periods in the relative sunspot numbers. Chinese J.Geophys. (in Chinese) , 2004, 47(5): 743-746. |
| [36] | 韩永志, 马利华, 尹志强. 极移振幅主要周期分量的时变特征. 地球物理学进展 , 2006, 21(3): 798–801. Han Y Z, Ma L H, Yin Z Q. Time-variation of periodic components of polar motion amplitude. Progress in Geophysics (in Chinese) , 2006, 21(3): 798-801. |
| [37] | Thomson D J, Robbins M F, Maclennan C G, Lanzerotti L J. Spectral and windowing techniques in power spectral analyses of geomagnetic data. Phys.Earth PLanet.Int. , 1976, 12(2-3): 217-231. DOI:10.1016/0031-9201(76)90050-9 |
| [38] | Torrence C, Compo G P. A practical guide to wavelet analysis. Bull.Amer.Meteorol.Soc. , 1998, 79(1): 61-78. DOI:10.1175/1520-0477(1998)079<0061:APGTWA>2.0.CO;2 |
| [39] | Farge M. Wavelet transforms and their applications to turbulence. Annu.Rev.Fluid Mech. , 1992, 24(1): 395-458. DOI:10.1146/annurev.fl.24.010192.002143 |
| [40] | Bondi H, Gold T. On the generation of magnetism by fluid motion. Mon.Not.R.Astron.Soc. , 1950, 110: 607-611. DOI:10.1093/mnras/110.6.607 |
| [41] | Lowes F J. Spatial power spectrum of the main geomagnetic field, and extrapolation to the core. Geophys.J.R.Astr.Soc. , 1974, 36(3): 717-730. DOI:10.1111/j.1365-246X.1974.tb00622.x |
| [42] | Zatman S, Bloxham J. Torsional oscillations and the magnetic field within the Earth' s core. Nature , 1997, 388(6644): 760-763. DOI:10.1038/41987 |
| [43] | Dickey J O, de Viron O. Leading modes of torsional oscillations within the Earth's core. Geophys.Res.Lett. , 2009, 36: L15302. DOI:10.1029/2009GL038386 |
 2010, Vol. 53
2010, Vol. 53


