2. 中国矿业大学资源与地球科学学院, 江苏徐州 221116
2. School of Resource and Earth Science, China University of Mining & Technology, Xuzhou, Jiangsu 221116, China
视电阻率是瞬变电磁勘探方法中经常采用的参数,该参数可以形象地表达地下电性结构.有关地面瞬变电磁法视电阻率定义(早期和晚期)及全区视电阻率求解方面的研究已比较深人,其中以文献[1~10]最具代表性.这些研究主要探讨全区视电阻率方程的求解方法,以得出更逼近模型“真”电阻率的全区视电阻率公式.若按激发源不同划分,Das[1, 2]和翁爱华[5]以偶极源激发的磁场为研究对象,而严良俊、朱苏刘、白登海、王华军等[3, 4, 6~11]则着重研究中心回线装置的视电阻率换算.就地面瞬变电磁法而言,中心回线装置和重叠回线装置是经常采用的装置形式;而对于矿井瞬变电磁法而言,重叠回线装置是巷道内可以实施的仅有的有效装置之一,也是最常用的收-发形式(其他的两种形式为白登海与加拿大GEONICS公司合作开发的EM-47HP仪器所采用的共面和共轴方式).然而,重叠回线装置采用的视电阻率转换方法多为半空间中心回线源晚期视电阻率公式[12],全区视电阻率解释方法还尚未采用;尽管已有研究者根据实验结果给出了全空间重叠回线晚期视电阻率的经验公式[13],但该公式仅为由不同地质情况决定的全空间系数与半空间中心回线晚期视电阻率公式的乘积,且未从理论上对全空间系数进行深人讨论,其理论正确性也未得到验证.实际上,矿井瞬变电磁视电阻率仍然可以由回线源瞬变场近似定义(早期、晚期视电阻率),或精确定义(全区视电阻率),并可以此分析全空间视电阻率与半空间视电阻率换算公式的精确性和适用性.
2 视电阻率定义 2.1 地面瞬变电磁法视电阻率在均匀半空间情况下,水平圆形回线中心处的瞬变响应(磁场的垂直分量与感应电动势)为[14, 15]
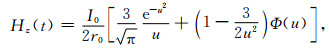
|
(1) |
和
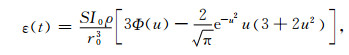
|
(2) |
式中,I0为供电电流,t为观测时间,μ为均匀半空间磁导率(可近似取为真空磁导率μ0), S为接收线圈的等效面积,r0为发射线圈半径;若线圈是边长为b的方形回线时,r0为等效半径,且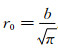
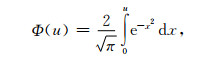
|
(3) |
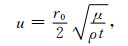
|
(4) |
当ρt→∞时,可由式(1)和式(2)得到中心回线晚期响应为
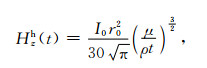
|
(5) |
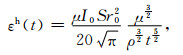
|
(6) |
式(4)中设X=u,并且令核函数
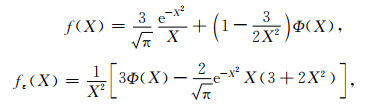
|
则式(1)和式(2)变为
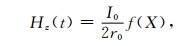
|
(7) |

|
(8) |
同时,由式(4)得到
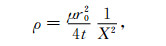
|
(9) |
若介质不均匀,求解(7)式(或(8)式)和(9)式得到的电阻率ρ为地面瞬变电磁法全区视电阻率.
由(5)式和(6)式可得到中心回线晚期视电阻率公式分别为

|
(10) |
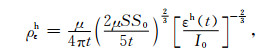
|
(11) |
式中,S0=πr02为发射线圈的面积.
2.2 矿井瞬变电磁法视电阻率均匀全空间介质中的水平圆形回线发射框中心的瞬变响应(磁场的垂直分量与感应电动势)为[14]

|
(12) |
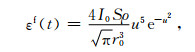
|
(13) |
式中参数与半空间公式相同.
当ρt→∞时,由式(12)和式(13)得到中心回线晚期响应为
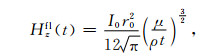
|
(14) |
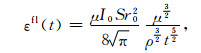
|
(15) |
若在式(12)和式(13)令核函数
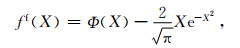
|
(16) |
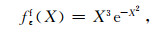
|
(17) |
则可以得到
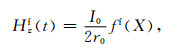
|
(18) |
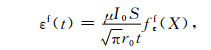
|
(19) |
且全空间视电阻率公式仍由(9)式定义.
由(14)式和(15)式得到中心回线晚期视电阻率公式分别为
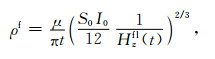
|
(20) |
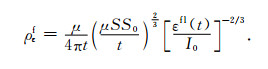
|
(21) |
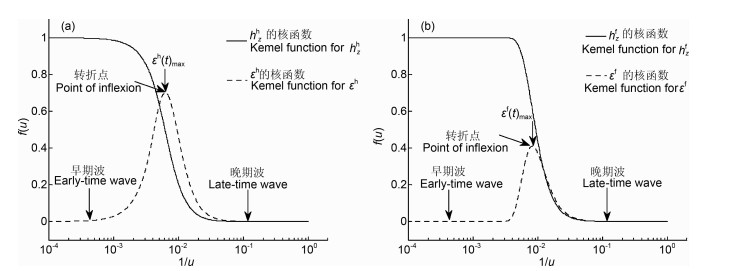
将公式(10)和(20)以及公式(11)和(21)进行比较,无论以磁场还是感应电动势计算的全空间晚期视电阻率值都是半空间晚期视电阻率的(5/2)2/3(约为1.842)倍.另一方面,由图 1可以看出,全空间全区视电阻率核函数与半空间核函数具有相似的特征,hz的核函数均为u的单值函数,由此易求得方程(7)和(18)的惟一解.但是,全空间hz核函数早期场持续时间较长,表现为图 1b中曲线首支在很长时间范围内恒定为1,之后迅速衰减.ε的核函数均为双值函数,其解有三种情况:当归一化感应电动势与转折点(Point of inflexion)处的核函数值相等时,方程(8)和(19)有惟一解;大于转折点处的核函数值时,无解;小于转折点处的核函数值时有两个解,这两个解分别对应于早期解和晚期解.
|
图 1 空间(a)和全空间(b)核函数曲线 Fig. 1 Kernel function curves for half space (a) and full space (b) |
文献[10]提出了一种半空间全区视电阻率的直接解法,该方法利用半空间瞬变响应曲线的平移伸缩特性,直接对全区视电阻率进行求解.王华军[10]的研究表明,该方法无需迭代和求解非线性方程,计算速度快,精度高,并可以获得唯一解.基于这种方法的诸多优点,现对该方法在全空间全区视电阻率计算中的适用性进行讨论.
首先将(4)式改写为: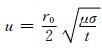
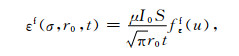
|
(22) |
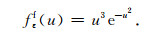
|
(23) |
(1)令
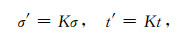
|
(24) |
式中,K为常数.则有
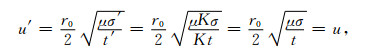
|
(25) |
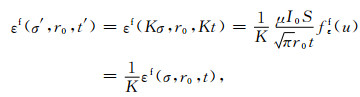
|
(26) |
即
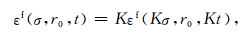
|
(27) |
(2)令
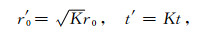
|
(28) |
则有
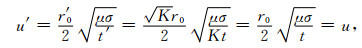
|
(29) |
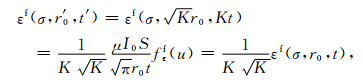
|
(30) |
即
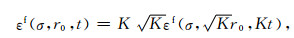
|
(31) |
且由式(27)和式(31)可得
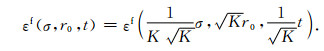
|
(32) |
综合上述讨论可知,全空间瞬变电磁响应曲线也具有平移伸缩特性,因此文献[10]提出的平移算法不仅适用于半空间全区视电阻率的计算,也适用于全空间瞬变电磁场.
4.2 其他计算方法 4.2.1 逆样条插值方法文献[7]提出了一种求解大回线源全区视电阻率的逆样条插值方法,现基于该方法对全空间瞬变电磁场全区视电阻率的求解进行讨论.
归一化的全空间全区视电阻率f(u)曲线特征与半空间相似(图 1),函数f(u)也是非单调的,它在dfεf(u)/du=0处,即当u=1.2247时有极大值0.4099.点u=1.2247为曲线的转折点,该点将整个瞬变过程划分为早期段(u>1.2247)和晚期段(u<1.2247),在各个阶段分别施行逆样条插值,最后构成整个时间段上的视电阻率曲线.逆样条插值方法概述如下:
若函数y=f(u)在区间[ui,uj]内满足反函数定理中的条件,则存在反函数u=g(y),从而求解原函数y=f(u)的零点可归结为函数u=g(y)在y=0处的函数值,对节点(yi,ui)(i=1,2,…,n)采用样条插值公式使之逼近g(y),进而可得y=0点处的差值.
由此可见,该方法在计算全空间全区视电阻率时也是可行的.
4.2.2 二分搜索算法文献[11]介绍了一种全区视电阻率的二分搜索算法,该算法的实质为数值分析中的二分法的一种应用,文献中采用该方法的前提条件是在任意时刻感应电动势随电阻率的增大而单调下降,在此条件下不断变化电阻率的取值区间,使同一采用时刻区间内某一电阻率的理论感应电动势与实测值相近,则可取该电阻率为所求视电阻率.实际上,由全空间感应电动势方程(13)可知,全空间中任意时刻感应电动势也随电阻率的增大而单调下降,因此,该方法也适用于求解全空间全区视电阻率.
5 算例与实例 5.1 理论数据视电阻率计算图 2为由理论数据计算的均匀全空间晚期和全区视电阻率曲线,全空间电阻率理论值为10 Ωm,图 2a采用半空间晚期和全区视电阻率公式,图 2b采用全空间晚期和全区视电阻率公式.分析图 2可知,采用半空间视电阻率公式计算结果与真值的相对误差均大于42%(无论晚期公式还是全区公式).而全空间晚期视电阻率公式计算结果与真值的相对误差在早期较大,上限为5%;过渡期和晚期的相对误差小于0.56%,并随采样延时的增加而逐渐减小.由此可见,应用半空间视电阻率公式处理全空间资料,其结果与真实全空间介质电性偏离严重,而全空间晚期视电阻率处理晚延时资料能达到令人满意的效果,实际计算以精确电阻率公式(全区公式)为佳.

|
图 2 均匀全空间视电阻率 ρεh和ρεf为半空间和全空间晚期视电阻率公式,ρallh和ρallf为半空间和全空间全区视电阻率公式,42%、5%、0.56%和0.5%为计算值与真值的相对误差. Fig. 2 Apparent resistivity in homogeneous full-space |
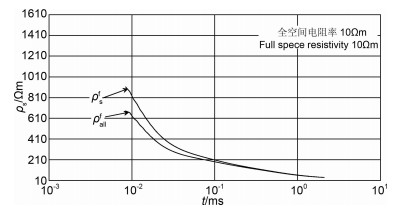
图 3为由三维正演数据计算的巷道全空间视电阻率曲线,巷道围岩电阻率为10 Ωm.由于巷道的影响,转化后的全区视电阻率曲线并不是一条直线,但比晚期视电阻率更快逼近真值.研究表明[16],巷道影响下的全空间视电阻率值普遍要高于均匀全空间视电阻率值,因此,在较晚延时该曲线才能逼近真值.
|
图 3 巷道全空间视电阻率 Fig. 3 Apparent resistivity in roadway full-space |
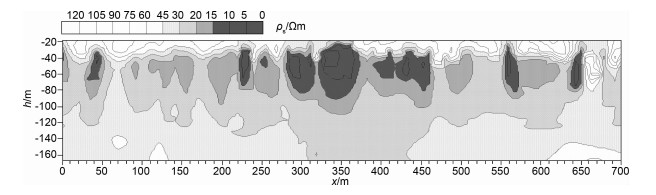
为查明某矿机巷底板含水构造发育情况,在巷道内进行瞬变电磁法探测,图 4为采用半空间晚期视电阻率公式绘制的视电阻率拟断面图,深度计算采用文献[13]研究的矿井瞬变电磁法时间-深度转换公式.从图中可以看出,横坐标为300 m和500 m附近有两个低阻异常区,深度上限为35 m,下限未知,但要大于110 m,推断该处有导水构造发育,后经钻孔验证属实.图 5为由同一探测数据绘制的视电阻率拟断面图,与图 4不同的是采用全空间全区视电阻率公式计算.由该图解释的两低阻异常区横坐标与图 4相同,但是深度范围则可以确定,为30 m和80 m之间;同时,该图中的电阻率差异更大,异常区范围更加明显.由此可知,全空间全区视电阻率公式适合矿井瞬变电磁法数据资料处理,与半空间晚期视电阻率公式相比具有更好的效果.

|
图 4 采用半空间晚期视电阻率ρεh计算的视电阻率断面图 Fig. 4 Section diagrams for apparent resistivity (calculated by half-space"late time"formula ρεh) |
|
图 5 采用全空间全区视电阻率ρallf计算的视电阻率断面图 Fig. 5 Section diagrams for apparent resistivity (calculated by full-space"all time"formula ρallf) |
矿井瞬变电磁法理论研究仍处于起步阶段,全空间效应和巷道影响的存在必然使全空间响应特征有别于半空间,常规的矿井实测资料解释方法也需要不断改进和补充.本文推导的全空间视电阻率计算方法(晚期和全区)在资料处理和解释中的应用效果要优于常规方法,全空间视电阻率计算方法与真值的相对误差较低,计算后的电阻率差异明显,而常规方法的误差较大,由此计算的异常响应的深度范围难以确定.文中的全空间视电阻率公式既适用于中心回线方式,也适用于重叠回线方式,由于井下以使用重叠回线居多,故文中正演资料和实测数据均采用此装置.基于全空间和半空间瞬变电磁视电阻率值相差一个常数倍的关系,计算全空间瞬变电磁视电阻率时可应用目前已有的半空间算法,但须将解释结果乘以一个常数.
致谢感谢中国地质科学院地球物理地球化学勘查研究所蒋邦远老师给予的指导.
| [1] | Das U C. Apparent resistivity curves in controlled-source electromagnetic sounding directly reflecting true resistivities in a Layered Earth. Geophysics , 1995, 60(1): 53-60. DOI:10.1190/1.1443762 |
| [2] | Das U C. Frequency-and time-domain electromagnetic responses of layered earth-a multiseparation, multisystem approach. Geophysics , 1995, 60(1): 285-290. DOI:10.1190/1.1443756 |
| [3] | 严良俊, 胡文宝, 陈清礼, 等. 长偏移距瞬变电磁测深的全区视电阻率求取及快速反演方法. 石油地球物理勘探 , 1999, 34(5): 532–538. Yan L J, Hu W B, Chen Q L, et al. The estimation and fast inversion of all-time apparent resistivities in long-offset transient electromagnetic sounding. OGP (in Chinese) , 1999, 34(5): 532-538. |
| [4] | 苏朱刘, 胡文宝. 中心回线方式瞬变电磁测深虚拟全区视电阻率和一维反演方法. 石油物探 , 2002, 41(2): 216–221. Su Z L, Hu W B. Pseudo-full-region apparent resistivity and its one-dimensional inversion for center-loop-line configuration TEM data. Geophsical Prospecting for Petroleum (in Chinese) , 2002, 41(2): 216-221. |
| [5] | 翁爱华, 陆冬华, 刘国兴. 利用连分式定义瞬变电磁法全区视电阻率研究. 煤田地质与勘探 , 2003, 31(3): 56–59. Weng A H, Lu D H, Liu G X. Definition of whole zone apparent resistivity for transient electromagnetic method of current dipole source. Coal Geology and Exploration (in Chinese) , 2003, 31(3): 56-59. |
| [6] | 白登海, MaxwellA Meju, 卢健, 等. 时间域瞬变电磁法中心方式全程视电阻率的数值计算. 地球物理学报 , 2003, 46(5): 697–704. Bai D H, M A Meju, Lu J, et al. Numerical calculation of all-time apparent resistivity for the central loop transient electromagnetic method. Chinese J.Geophys (in Chinese) , 2003, 46(5): 697-704. |
| [7] | 熊彬. 大回线瞬变电磁法全区视电阻率的逆样条插值计算. 吉林大学学报(地球科学版) , 2005, 35(4): 515–519. Xiong B. Inverse spline interpolation for the calculation of all-time resistivity for the large-loop transient electromagnetic method. Journal of Jilin University (Earth Science Edition) (in Chinese) , 2005, 35(4): 515-519. |
| [8] | 李建平, 李桐林, 赵雪峰, 等. 层状介质任意形状回线源瞬变电磁全区视电阻率的研究. 地球物理学进展 , 2007, 22(6): 1777–1780. Li J P, Li T L, Zhao X F, et al. Study on the TEM all-time apparent resistivity of arbitrary shape loop source over the layered medium. Progress in Geophysics (in Chinese) , 2007, 22(6): 1777-1780. |
| [9] | 许建荣, 李爱勇, 杨生. TEM中心回线法瞬变磁场求取和全区视电阻率计算. 地质与勘探 , 2008, 44(6): 62–68. Xu J R, Li A Y, Yang S. Calculation of transient magnetic field and all time apparent resistivity based on central TEM loops method. Geology and Prospecting (in Chinese) , 2008, 44(6): 62-68. |
| [10] | 王华军. 时间域瞬变电磁法全区视电阻率的平移算法. 地球物理学报 , 2008, 51(6): 1936–1942. Wang H J. Time domain transient electromagnetism all time apparent resistivity translation algorithm. Chinese J.Geophys. (in Chinese) , 2008, 51(6): 1936-1942. |
| [11] | 陈清礼. 瞬变电磁法全区视电阻率的二分搜索算法. 石油天然气学报 , 2009, 31(2): 45–49. Chen Q L. Searching algorithm for full time apparent resistivity from TEM electromotive force data. Journal of Oil and Gas Technology (in Chinese) , 2009, 31(2): 45-49. |
| [12] | Ward S H, Hohmann G W.Electromagnetic theory for geophysical applications.In:Misac N Nabighian ed.Electromagnetic methods in applied geophysics-theory.SEG, 1987 http://www.oalib.com/references/16629586 |
| [13] | 于景邨. 矿井瞬变电磁法勘探. 徐州: 中国矿业大学出版社, 2007 . Yu J T. Mine Transient Electromagnetic Prospecting (in Chinese). Xuzhou: China University of Mining and Technology Press, 2007 . |
| [14] | Kaufman A A, Eaton P A. The Theory of Inductive Prospecting. New York: Elsevier, 2001 . |
| [15] | 米萨克N.纳比吉安主编.勘查地球物理电磁法(第一卷:理论).赵经祥, 王艳君译.北京:地质出版社, 1992. Nabigian N M.Electromagnetic Methods in Applied Geophysics (Volume 1)(in Chinese).Translated by Zhao J X, Wang Y J.Beijing:Geological Publishing House, 1992 |
| [16] | 岳建华, 杨海燕. 矿井瞬变电磁法三维时域有限差分数值模拟. 地球物理学进展 , 2007, 22(6): 1904–1909. Yue J H, Yang H Y. 3D finite difference time domain numerical simulation for in-mine TEM. Progress in Geophysics (in Chinese) , 2007, 22(6): 1904-1909. |
 2010, Vol. 53
2010, Vol. 53


