大量的野外电磁观测表明,地震孕育和发生的过程中可能会伴随一定的电磁异常变化[1~13],而且这些变化呈现出一定的特征,地震电信号的选择性现象就是其中令人关注的特征之一[14~16].希腊的三位物理学家Varotsos,Alexopoulos,和Nomicos(简称VAN)提出了利用地震电信号及其选择性特征来进行地震预报的VAN方法[16~18].但由于地震孕育过程和地球介质的复杂性,地震电信号的产生机制、远距离传播、选择性等问题的物理解释尚没有公认的、满意的答案,因此,VAN方法一直存在着激烈的争论[19~21].
而要合理地解释各种地震电信号观测资料,必须从信号的源效应和传播效应两方面入手.在源效应方面,部分从室内实验到理论模型等探索研究为地震电信号的产生机制提供了一定的依据[22~26].在传播效应方面,也有学者分别尝试从物理模拟实验和简单模型的数值模拟角度来解释地震电信号的选择性现象[14, 27~29],而最近基于有限元方法[30]的三维数值模拟研究表明,特定的地下导电通道可以较好地解释2000年日本伊豆火山型群发地震期间新岛台记录到的地震电信号的选择性现象[31].虽然该解释尚有待新岛地区的电磁勘探资料等证据的支持,但与以前简单二维模型的数值模拟研究相比,该三维有限元数值模拟研究为进一步模拟更接近于实际野外条件的地震电信号选择性问题奠定了一定的基础.
由于边界条件、模型参数等的选取可能直接影响数值模拟的结果,因此,为考察以往研究得到的海洋-陆地分布等地表介质电性非均匀性[14, 27, 28]以及地下特定导电通道[29, 31]这两种不同的地震电信号选择性问题解释机制的适用性,并避免边界条件、模型参数等因素的影响导致不准确甚至错误结论的可能性,有必要评估上述因素对地震电信号选择性数值模拟的影响,以增强数值模拟在解释实际地震电信号选择性问题的可信度.为此,本文暂不考虑电磁信号的具体产生机制以及物理模拟实验方面的研究,而是从数值模拟计算的角度,重点评估地震电信号选择性数值模拟及其可能的影响因素.考虑到本文所采纳的有限元方法是一种常规的数值计算方法,第2节将不具体介绍有限元方法本身,而只是简要提及本研究涉及的具体问题以及算法的基本思路.第3节将利用COMSOL公司开发的有限元方法的商业软件COMSOL Multiphysics(http://www.comsol.com),选取不同的边界条件、模型参数、介质电性结构等,对设计的部分模型进行三维数值模拟计算,通过模拟结果的对比分析,考察不同因素对数值模拟结果的影响.最后,第4节将在分析本研究得到结果的基础上,探讨数值模拟在地震电信号选择性研究方面的适用性问题.
2 方法有限元方法[30]具有将研究区域剖分成有限个任意的小单元的特点,因此,该方法适于物性复杂分布的各类问题的研究,尤其是随着计算机的发展,有限元方法在解决具有复杂结构的地球物理问题方面得到了广泛的应用.
由于最有代表性的地震电信号的选择性现象是针对直流地电位观测而言的[16],因此,本研究仅讨论满足以下泊松方程的稳恒电流源问题[30, 32],
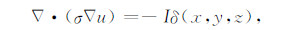
|
(1) |
其中,σ为模型各点电导率,u为模型各点电位,I为稳恒电流源电流强度,δ(x,y,z)为狄拉克(Dirac)函数.
由于方程(1)的电位u在源点的奇异性,直接求解将会带来很大的误差,尤其是在源点及其邻近区域,因此,本研究采用异常电位有限元方法[30]进行计算,即先解析地求出给定稳恒电流源下均匀半空间介质的正常电位,然后用有限元方法计算该稳恒电流源在电性异常体作用下产生的异常电位,两者叠加即可得到各节点的总电位值.具体的三维有限元计算基于商业软件COMSOL Multiphysics来实现,其网格的划分采用四面体剖分方式,并遵循源区以及感兴趣区域网格加密的原则.
由于本文关注的是地震电信号选择性问题的数值模拟,尽管地震电信号的的具体产生机制还存在争议,但迄今在地震电信号关联问题研究方面常采纳的做法是用偶极直流电流源(相当于两个正负点电流源的叠加)来近似.因此,本文在以下的模型中均采用偶极直流电流源来近似模拟地震电信号的源.
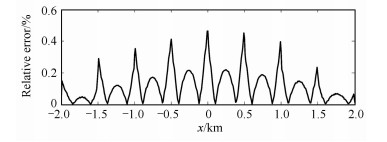
3 结果作为对有限元算法有效性的一种检验,同时也为了定量评估边界条件和所选择的计算区域大小等对计算结果的影响,我们首先选择了一个有解析解的三层水平层状介质简单模型,一个偶极电流源位于最底层介质内(图 1).由于该模型有解析解,为检验本研究使用的商业有限元软件算法的有效性,我们在边界面上选择第一类边界条件[30],并按相应的解析电位值赋值.图 2给出了模型计算区域在x,y,z方向分别为20km,20km,10km(图 1为其经过偶极电流源的xz垂直剖面)时,利用该三维有限元软件计算得到的图 1所示垂直剖面的地表电场结果与解析解在源附近区域(x:-2km~2km)的相对误差(定义为计算值与解析解之差与解析解的比值的绝对值).由图可见,地表电场计算结果与解析解非常一致,源附近区域最大相对误差小于0.5%.需要说明的是,由于该模型在距源区较远处的电场解析解的绝对值很小(接近0)(图 3a),距源较远处的相对误差其实已无法反映计算结果的真实偏差,因而没有太大的参考意义.

|
图 1 一个三层水平层状介质模型(垂直剖面图).一个104 Am偶极电流源位于最底层介质内 Fig. 1 A three-layered model (a view of vertical cross-section) with an 104 Am dipole current source in the lowest layer |
|
图 2 经过偶极电流源的垂直剖面沿x方向地表电场计算结果与解析解的相对误差 Fig. 2 Relative error of the computed electric field on the surface along x direction with respect to the analytical one |
|
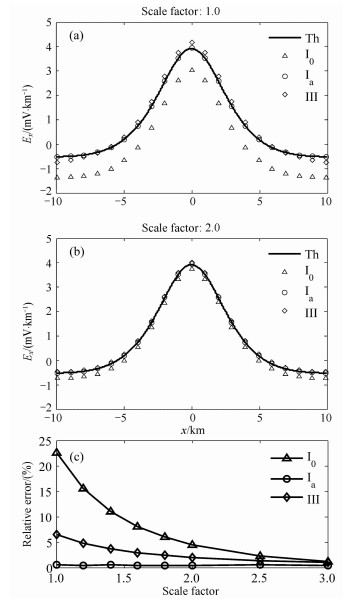
图 3 (a)图 1模型中计算区域为20 km×20 km×10 km (尺度因子倍率为1.0)时不同边界条件得到的经过偶极电流源垂直剖面的沿x方向地表电场及其解析解.图中Th表示模型的解析解, Ⅰ0表示边界取.电位值的第一类边界条件, Ⅰa表示边界取相应的解析电位值的第一类边界条件, Ⅲ表示边界取第三类边界条件.(b)图 1的模型中增大计算区域为40 km×40 km×20 km, (尺度因子倍率为2.0)时不同边界条件得到的沿x方向地表电场及其解析解.(c)不同边界条件以及计算区域对应的x=0的地表电场计算值与解析解的相对误差 Fig. 3 (a) The electric field on the surface along x direction computed by using different type of boundary condition.The 3D calculated region is 20 km×20 km×10 km, which is set as the untt region (i.e., scale factor is 1.0).The analytical electric field is also given in the same figure for reference.(b) Similar figure as (a) with a calculated region of 40 km×40 km×20 km (i.e., scale factor is 2.0).(c) Relative error of the computed electric field on the surface along x direction at x=0 for various boundary conditions and calculated regions with respect to the analytical one |
为了考察不同边界条件的选取对计算结果的影响,我们分别选取了第一类边界条件和第三类边界条件(混合边界条件)[30],其中,对于第一类边界条件,我们又分在边界处取相应模型的解析电位值以及直接取0电位值(无穷远处的电位值)两种情况来讨论.而为了评估模型的计算区域大小的选取对计算结果的影响,我们以图 1中给出的模型大小(x,y,z方向的大小分别为20km,20km,10km)为基准(尺度因子倍率为1.0),计算区域在x,y,z三个方向均按等比率的尺度因子倍率选取,倍率分别取1.0,1.2,1.4,1.6,1.8,2.0,2.5,3.0.图 3a为计算区域为20km×20km×10km(尺度因子倍率为1.0)时取不同边界条件计算得到的经过偶极电流源垂直剖面的地表电场沿x方向的结果,由图可见,由边界取0电位值的第一类边界条件得到的结果(三角形符号表示)明显偏离解析解(黑实线),而另两种边界条件下的结果与解析解非常一致.类似结论在增大计算区域时依然成立,例如,图 3b为计算区域取尺度因子倍率为2.0时的结果,虽然边界取0电位值的第一类边界条件得到的结果(三角形符号表示)依然偏离解析解(黑实线),但误差已明显随着计算区域的增大而减小.为了更清晰地反映边界条件以及计算区域对计算结果的影响,图 3c给出了x=0的地表电场计算值与解析解的相对误差的变化趋势.结果表明,在所选取的三种不同边界条件中,取相应模型的解析电位值的第一类边界条件下的相对误差最小,而取0电位值的第一类边界条件下的相对误差最大.相对误差一般会随着计算区域的增大而减小,当模型尺度因子倍率达到3.0时,所选取的三种不同边界条件计算结果的相对误差已非常接近.但需要指出的是,边界取相应模型的解析电位值时计算得到的相对误差并不随计算区域大小的改变而变化.
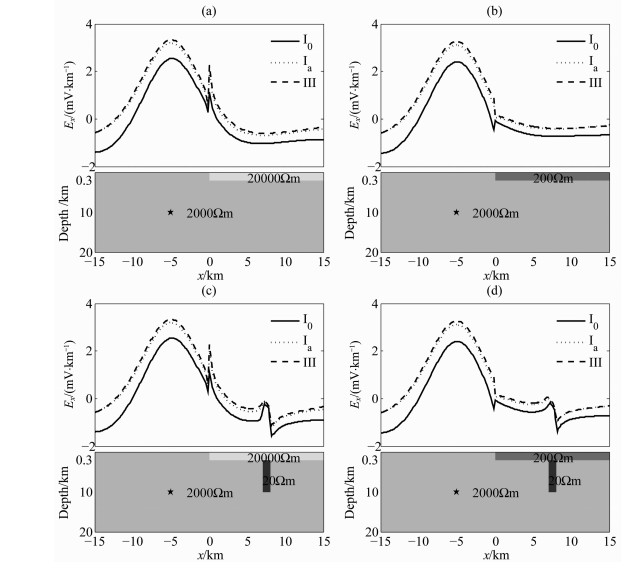
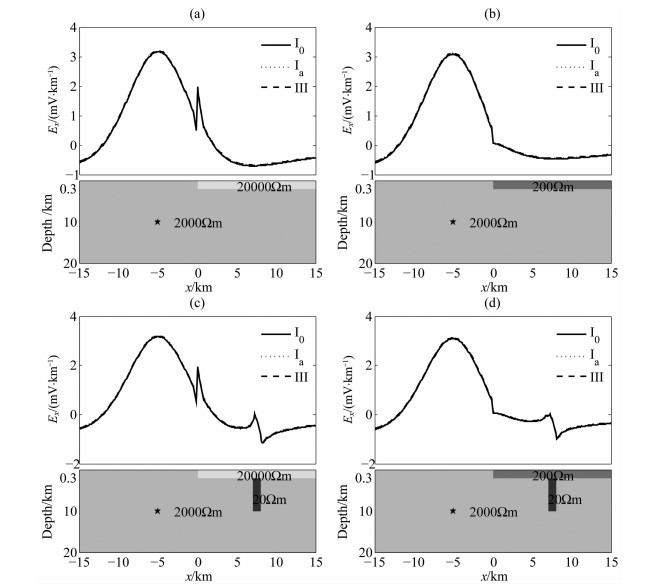
在地震电信号选择性问题研究方面,已有的物理模拟实验[14, 27, 28]和数值模拟[29, 31]研究表明地表介质的电性非均匀性、地下特定的导电通道等是导致地表地震电信号选择性的可能因素.为此,我们分别设计了含有地表介质电性差异和地下特定导电通道的模型(图 4),并分别给出了对应模型(计算区域为30km×30km×20km,尺度因子倍率为1.0)在取不同边界条件时地表电场的计算结果.其中,图 4(a,b)的模型分别对应不同地表介质电性分布,而图 4(c,d)的模型分别由图 4(a,b)的模型中加入一个如图所示的地下导电通道而构成.我们再次看到边界取0电位值的第一类边界条件下的结果(黑实线)明显偏离另两种边界条件下的结果,表明所讨论的几种边界条件中,边界取0电位值(无穷远电位值)时的计算误差最大,而且与图 3c类似,该误差也随计算区域的增大而减小.作为一个例子,图 5给出了模型尺度因子倍率为3.0(即计算区域为90km×90km×60km)与图 4对应的计算结果,可见当选取的计算区域足够大时,不同边界条件计算得到的结果也趋于一致.图 5还表明,地表介质的电性差异以及地下的导电通道等直接影响了地表电场的分布,这种影响在地表介质的分界附近以及导电通道在地表的投影附近尤其明显.
|
图 4 地表介质电性差异和地下特定导电通道对地表电场的影响(模型计算区域为30 km×30 km×20 km, 尺度因子倍率为1.0).-个偶极电流源位于地下10 km处(如图中五角星所示).不同边界条件的符号说明同图 3 Fig. 4 Possible influences of surface inhomogeneity of resistivity and underground conductive channel to the electric field on the surface, with a calculated region of 3 0 km×3 0 km×2 0 km (i.e., scale factor is 1.0).A dipole current source is located at 10 km depth as marked by the black star |
|
图 5 地表介质电性差异和地下特定导电通道对地表电场的影响(模型计算区域为90km×90km×60km,尺度因子倍率为3.0).-个偶极电流源位于地下10 km处(如图中五角星所示).不同边界条件的符号说明同图 3 Fig. 5 Possible influences of surface inhomogeneity of resistivity and underground conductive channel to the electric field onthe surface, with a calculated region of 9 0 km×9 0 km×6 0 km (i.e., scale factor is 3.0).A dipole current source is located at 10 km depth as marked by the black star |
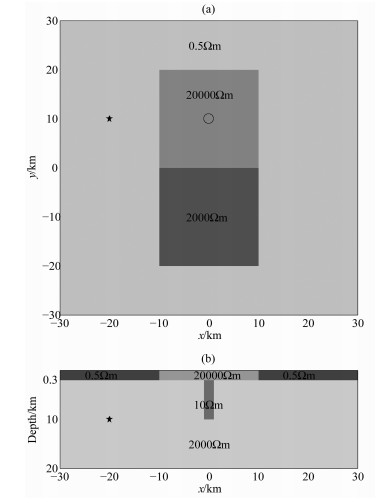
物理模拟实验[14, 27, 28]研究表明地表海洋-陆地分布是导致地震电信号选择性现象的一种可能原因.考虑到海陆电性的巨大差异,图 6给出了一个同时包含地表海陆分布、陆地电性差异以及地下导电通道的模型.模型尺度因子倍率为1.0时对应的计算区域为60km×60km×20km(如图 6所示).图中五角星给出了偶极电流源所在位置(地下10km处).一垂直导电通道位于陆地高阻区域正中心处,通道的上端刚好位于陆地高阻表层下方,而下端延伸至地下10km处(图 6).图 7a给出了模型尺度因子倍率为2.0时选取第三类边界条件(混合边界条件)计算得到的地表电场分布.结果显示在海陆交界区域附近(尤其是离源较近的一侧)电场明显增强,地下导电通道上方附近的电场也有所增强.
|
图 6 同时包含地表海陆分布、陆地电性差异以及地下导电通道的模型示意图.(a)模型在地表的分布,五角星为偶极电流源在地表的投影,空心圆为地下导电通道在地表的投影;b)经过偶极电流源和地下导电通道的剖面图,五角星为偶极电流源所在位置.模型尺度因子倍率1.0对应的计算区域为60km×60km×20km Fig. 6 A sketch model consists of ocean-land distribution, land resistivity inhomogeneity, and underground conductive channel.(a) Model distribution on the surface.The star and circle indicates the projection on the surface of the dipole current source and the underground conductive channel, respectively, (b) A cross-section including the dipole current source and the underground conductive channel.The model scale factor of1.0 correspondsto a calculated region of 60 km×60 km×20 km |
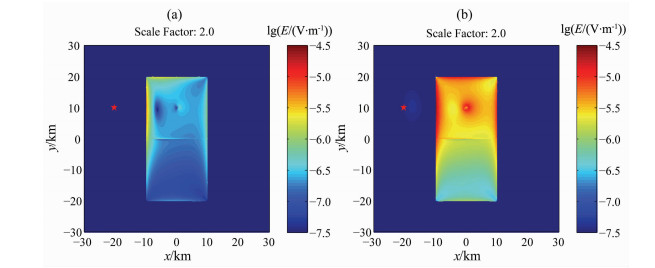
为了进一步考察地下导电通道对地表电场的影响,在图 6的模型中假定在地下10km处还存在一个连通偶极电流源和垂直导电通道下端的水平导电通道.图 7b为该模型在尺度因子倍率为2.0时选取第三类边界条件(混合边界条件)计算得到的地表电场分布.结果同样表明在海陆交界区域附近(尤其是离源较近的一侧)电场与无水平导电通道(图 7a)相比显著增强,与图 7a不同的是,地下导电通道上方附近的电场也显著增强.
|
图 7 模型尺度因子倍率为2.0(即计算区域为120km×120km×40km)时计算得到的地表电场分布.(a)图 6模型计算得到的结果.(b)图 6模型中增加一个在地下10 km处连通偶极电流源和垂直导电通道下端的水平导电通道后计算得到的结果 Fig. 7 Electric field distribution on the surface obtained from the calculation based on a model size of 120 km×120 km×40 km (i.e., a scale factor of 2.0).(a) Results of the model given in Fig. 6.(b) Results of the model after adding in Fig. 6 a horizontal conductive channel at a depth of 10 km, which connects the dipole current source and the vertical underground conductive channel |
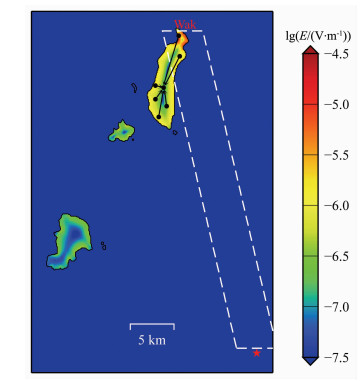
从数值模拟的角度来解释地震电信号的选择性现象的研究目前还并不多见,但已有的这些地震电信号选择性数值模拟探索初步表明,特定的地下导电通道是导致地震电信号选择性现象的一个非常可能的原因[29, 31],当然,进一步的证据尚有待观测到地震电信号选择性现象的台站周边的电磁勘测查资料的支持.需要说明的是,最近基于有限元方法的三维数值模拟研究显示特定的地下导电通道似乎可以较好地解释2000年日本伊豆火山型群发地震期间新岛台记录到的地震电信号的选择性现象[31],图 8给出了基于该区域的三维模型计算得到的地表电场分布的一个例子,该结果显示在地下10km处的水平导电通道(图中白色虚线为其地表投影)和新岛北部Wak测点附近地下的局部垂直导电通道的联合作用下,该岛北端的电场明显增强,与新岛所有测线中只有Wak记录到地震电信号这种选择性现象的观测报告[2, 33]吻合.而地表海陆分布以及地表电性差异作为导致地震电信号选择性现象的另一种可能原因虽然得到了部分物理模拟实验[14, 27, 28]的支持,但前面提到的关于日本新岛台地震电信号选择性的数值模拟结果表明地表海陆分布以及地表电性差异似乎并不能满意地解释新岛台记录到的地震电信号选择性现象[31].那么,到底这只是一个具体个案的结论,还是意味着特定的地下导电通道普遍比地表电性非均匀性能够更好地解释地震电信号的选择性现象呢?
要真正客观地回答上述问题,当然还需要积累并开展大量的有地震电信号选择性观测的个案的数值模拟研究.但其实仔细分析新岛台记录到的地震电信号选择性现象,并结合本文开展的部分数值模拟结果,也可能在一定程度上回答上述问题.事实上,由于新岛本身是一个狭长的小岛(图 8中最上方标有6条地电场测线的岛),尤其是记录到地震电信号的选择性地点仅限于新岛北端的小范围内[2, 33],该个案数值模拟得到的选择性现象是由地下导电通道所致的结论,可能与该个案的特殊性直接有关,因为该个案对应的伊豆群发地震是火山型地震,期间伴随显著的地下岩浆的运移[33, 34],因此极有可能形成地下的水平导电通道,如果在个别测点(例如该岛北端的Wak测点(图 8))存在局部的垂直导电通道,则比较容易如数值模拟结果所显示的那样导致地震电信号的选择性现象[31].另一方面,由于新岛北端很小,即使地表海陆分布对选择性有贡献,由于与局部垂直导电通道在其上方的影响叠加在一起,因此难以识别.本研究设计的如图 6所示的模型其实也是希望能在一定程度上加深对该问题的认识.当局部垂直导电通道在地表的投影区域与地表海陆交界区域能明显保持一定的空间距离时,图 7a的结果表明无论是地表海陆分布还是地下导电通道都能令其局部区域的电场增强,只是由于所设计的模型的源相对较远,导致整体电场强度有限.而引入地下水平导电通道后,如图 7b所示,不仅局部垂直导电通道上方附近的电场显著增强,地表海陆交界区域的电场也明显增强,而且这两种效果在空间上能够区别开来.因此,基于目前的数值模拟结果,我们并不能简单地认定地表电性非均匀性对地震电信号选择性现象的贡献一定不及地下导电通道.事实上,本研究似乎表明正是由于可能存在地下导电通道和地表电性非均匀性这两种因素的共同作用(双重放大效果),才更有利于导致地震电信号选择性现象的发生(图 7).
|
图 8 新岛台记录到的伊豆群发地震相关的地震电信号选择性现象的三维数值模拟结果的一个例子(根据文献[31]加工).模型除考虑了该地区的实际海洋-陆地分布之外,还考虑了新岛北部Wak测点附近地下的局部垂直导电通道和地下10 km处的由于岩浆运移等可能形成的水平导电通道(图中白色虚线为其地表投影).五角星表示偶极电流源的地表投影.带箭头的线表示新岛的6条地电场测线,其中,只有岛北端的Wak测点对应的测线记录到地震电信号 Fig. 8 An example of the 3D numerical simulation results of the SES selectivity phenomena associated with the Izu earthquake swarm recorded at Niijima station (modified after Ref.[31]).The red star represents the surface projection of the dipole current source.The model includes ocean-land distribution, a local vertical conductive channel under the Wak site, and a horizontal conductive channel with a width of 5 km (the dashed white lines indicate its projection on ground surface), possibly associated with underground magma migration.The resutt indicates the high sensitivity of the Wak site |
无论是对伊豆地震电信号选择性的个案研究[31]还是本文开展的模型分析均表明,基于商业有限元软件COMSOL Multiphysics的三维有限元数值模拟可以在地震电信号选择性问题研究中发挥一定的作用.本文对数值模拟的影响因素的分析表明,不同类型的边界条件、不同大小的计算区域、不同的介质电性参数以及地表介质电性非均匀性和地下特定导电通道等不同电性结构模型等都会对地震电信号选择性数值模拟结果造成一定的影响,因此,在实际数值模拟研究中需要对模型参数的选取进行必要的分析,以避免因模型参数选取不当导致模拟结果出现较大的误差,甚至因此而导致得出错误的结论;同时,在考察地表介质电性非均匀性和地下特定导电通道等在解释地震电信号选择性问题的适用性时,也需结合模型具体的电性结构和对比度等参数来进行综合分析.
| [1] | 韩鹏, 黄清华, 修济刚. 地磁日变与地震活动关系的主成分分析--以日本岩手县北部6.1级地震为例. 地球物理学报 , 2009, 52(6): 1556–1563. Han P, Huang Q H, Xiu J G. Principal component analysis of geomagnetic diurnal variation associated with earthquakes:case study of the M6.1 Iwate-ken Nairiku Hokubu earthquake. Chinese J.Geophy. (in Chinese) , 2009, 52(6): 1556-1563. DOI:10.3969/j.issn.0001-5733.2009.06.017 |
| [2] | 黄清华, 刘涛. 新岛台地电场的潮汐响应与地震. 地球物理学报 , 2006, 49(6): 1745–1754. Huang Q H, Liu T. Earthquakes and tide response of geoelectric potential field at the Niijima station. Chinese J.Geophy. (in Chinese) , 2006, 49(6): 1745-1754. |
| [3] | 黄清华. 地震电磁信号观测研究简述. 国际地震动态 , 2005, 11: 2–5. Huang Q. The state-of-the-art in seismic electromagnetic observation. Recent Developments in World Seismology (in Chinese) , 2005, 11: 2-5. |
| [4] | 汤吉, 赵国泽, 王继军, 等. 张北-尚义地震前后电阻率的变化及分析. 地震地质 , 1998, 20(2): 164–171. Tang J, Zhao G Z, Wang J J, et al. Variation and analysis of resistivity before and after the Zhangbei-Shangyi earthquake. Seismology and Geology (in Chinese) , 1998, 20(2): 164-171. |
| [5] | 赵国泽, 陆建勋. 利用人工源超低频电磁波监测地震的试验与分析. 中国工程科学 , 2003, 5(10): 27–32. Zhao G Z, Lu J X. Monitoring & analysis of earthquake phenomena by artificial SLF waves. Engineering Science (in Chinese) , 2003, 5(10): 27-32. |
| [6] | 赵国泽, 汤吉, 邓前辉, 等. 人工源超低频电磁波技术及在首都圈地区的测量研究. 地学前缘 , 2003, 10(Suppl.): 248–257. Zhao G Z, Tang J, Deng Q H, et al. Artificial SLF method and the experimental study for earthquake monitoring in Beijing area. Earth Science Frontiers (in Chinese) , 2003, 10(Suppl.): 248-257. |
| [7] | Zhao G Z, Zhan Y, Wang L F, et al. Electromagnetic anomaly before earthquakes measured by electromagnetic experiments. Earthquake Science , 2009, 22: 395-402. DOI:10.1007/s11589-009-0395-5 |
| [8] | Du A, Huang Q, Yang S. Epicenter location by abnormal ULF electromagnetic emissions. Geophys.Res.Lett. , 2002, 29(10): 1455. DOI:10.1029/2001GL013616 |
| [9] | Johnston M J S. Review of electric and magnetic fields accompanying seismic and volcanic activity. Surv.Geophys. , 1997, 18(5): 441-475. DOI:10.1023/A:1006500408086 |
| [10] | Hattori K, Serita A, Gotoh K. ULF geomagnetic anomaly associated with 2000 Izu Islands earthquake swarm, Japan. Phys.Chem.Earth , 2004, 29(4-9): 425-435. DOI:10.1016/j.pce.2003.11.014 |
| [11] | Fraser-Smith A C, Bernardi A, McGill P R, et al. Low-frequency magnetic field measurements near the epicenter of the M_s7.1 Loma Prieta earthquake. Geophys.Res.Lett. , 1990, 17(9): 1465-1468. DOI:10.1029/GL017i009p01465 |
| [12] | Nagao T, Enomoto Y, Fujinawa Y, et al. Electromagnetic anomalies associated with 1995 Kobe earthquake. J.Geodyn. , 2002, 33(4-5): 401-411. DOI:10.1016/S0264-3707(02)00004-2 |
| [13] | Zhang H, Zhao B, Zhao Y, et al. PS-100 anti-interference electrical observation system and its application to earthquake prediction study. Phys.Chem.Earth , 2006, 31(4-9): 172-181. DOI:10.1016/j.pce.2006.02.012 |
| [14] | Huang Q, Ikeya M. Seismic electromagnetic signals (SEMS) explained by a simulation experiment using electromagnetic waves. Phys.Earth Planet.Inter. , 1998, 109(3-4): 107-114. DOI:10.1016/S0031-9201(98)00135-6 |
| [15] | Orihara Y, Noda Y, Nagao T, et al. A possible case of SES selectivity at Kozu-shima Island, Japan. J.Geodyn. , 2002, 33(4-5): 425-432. DOI:10.1016/S0264-3707(02)00005-4 |
| [16] | Varotsos P. The Physics of Seismic Electric Signals. Tokyo: Terra Pub., 2005 . |
| [17] | Varotsos P, Alexopoulos K. Physical-properties of the variations of the electric-field of the earth preceding earthquake 1. Tectonophysics , 1984, 110(1-2): 73-98. DOI:10.1016/0040-1951(84)90059-3 |
| [18] | Varotsos P, Alexopoulos K. Physical-properties of the variations of the electric-field of the earth preceding earthquake 2. Tectonophysics , 1984, 110(1-2): 99-125. DOI:10.1016/0040-1951(84)90060-X |
| [19] | Geller R J. Debate on evaluation of the VAN method. Geophys.Res.Lett. , 1996, 23(11): 1291-1452. DOI:10.1029/96GL00742 |
| [20] | Lighthill S J. A Critical Review of VAN:Earthquake Prediction from Seismic Electrical Signals. Singapore: World Scientific Press, 1996 . |
| [21] | Uyeda S. In defence of VAN's earthquake prediction. Eos Tran.AGU , 2000, 81(1): 3. DOI:10.1029/00EO00005 |
| [22] | 郭自强, 罗祥麟, 钱书清, 等. 矿山爆炸中的电磁辐射. 地球物理学报 , 1999, 42(6): 834–840. Guo Z Q, Luo X L, Qian S Q, et al. Electromagnetic emission accompanying mine blasting. Chinese J.Geophy. (in Chinese) , 1999, 42(6): 834-840. |
| [23] | 郝锦绮, 钱书清, 高金田, 等. 岩石破裂过程中的超低频电磁异常. 地震学报 , 2003, 25(1): 102–111. Hao J Q, Qian S Q, Gao J T, et al. ULF electric and magnetic anomalies accompanying the cracking of rock sample. Acta Seismol.Sin. (in Chinese) , 2003, 25(1): 102-111. |
| [24] | Huang Q. One possible generation mechanism of co-seismic electric signals. Proc.Japan Acad. , 2002, 78(7): 173-178. DOI:10.2183/pjab.78.173 |
| [25] | Huang Q.Theoretical and experimental study on seismo-electric signals and earthquake-related phenomena[Ph.D.thesis].Japan:Osaka Univ., 1999 |
| [26] | Mizutani H, Ishido T, Yokokura T, et al. Electrokinetic phenomena associated with earthquakes. Geophys.Res.Lett. , 1976, 3(7): 365-368. DOI:10.1029/GL003i007p00365 |
| [27] | Huang Q, Ikeya M. Experimental study on the propagation of Seismic Electro Magnetic Signal (SEMS) using a mini-geographic model of the Taiwan strait. Episodes , 1999, 22(4): 289-294. |
| [28] | Huang Q H. Controlled analogue experiments on propagation of seismic electromagnetic signals. Chinese Sci.Bull. , 2005, 50(17): 1956-1961. DOI:10.1360/982004-312 |
| [29] | Sarlis N, Lazaridou M, Kapiris P, et al. Numerical model of the selectivity effect and the ΔV/L criterion. Geophys.Res.Lett. , 1999, 26(21): 3245-3248. DOI:10.1029/1998GL005265 |
| [30] | 徐世浙. 地球物理中的有限单元法. 北京: 科学出版社, 1994 . Xu S Z. FEM in Geophysics (in Chinese). Beijing: Science Press, 1994 . |
| [31] | Huang Q H, Lin Y F. Selectivity of seismic electric signal (SES) of the 2000 Izu earthquake swarm:a 3D FEM numerical simulation model. Proc.Japan Acad. , 2010, 86(3): 257-264. DOI:10.2183/pjab.86.257 |
| [32] | 柯敢攀, 黄清华. 井地电法的三维正反演研究. 北京大学学报(自然科学版) , 2009, 45(2): 264–272. Ke G, Huang Q. 3D forward and inversion problems of borehole-to-surface electrical method. Acta Scientiarum Naturalium Universitatis Pekinensis (in Chinese) , 2009, 45(2): 264-272. |
| [33] | Uyeda S, Hayakawa M, Nagao T, et al. Electric and magnetic phenomena observed before the volcano-seismic activity in 2000 in the Izu Island Region, Japan. Proc.Nat.Acad.Sci.USA , 2002, 99(11): 7352-7355. DOI:10.1073/pnas.072208499 |
| [34] | Huang Q H. Seismicity associated with the 2000 earthquake swarm in the Izu Island region. J.Asian Earth Sci. , 2006, 26(5): 509-517. DOI:10.1016/j.jseaes.2004.11.005 |
 2010, Vol. 53
2010, Vol. 53

