最近,郭桂红等[1]撰文讨论了沉积盆地中地震波速度与地层年龄的关系,建立了中国大陆沉积盆地中速度、深度和年龄之间的定量关系,认为这为利用地震波速度测定地层年龄提供了一种新的方法.笔者感到该文的主导思想有待商榷.
2 问题的由来文献[1]等根据Weatherby,Faust等对沉积盆地地震波速度、深度、地质时代的关系[2~7],提出了地球物理定年的设想[8].
但是国外学者讨论上述关系时是有一些特定条件的.
Baskell专门讨论了第三系砂泥岩的地震波速度与深度、岩性的关系[5],Stulken讨论的加利福尼亚的SanJoaquin Valley东南部的地震波速[6],Acheson则研究了加拿大西部的时-深和速度-深度关系[7].
前者只讨论第三系,后两者仅讨论某一地区.文献[1]把这一关系推广到了有960×104km2的中国的9个沉积盆地,这种外推便有很多不确定性.
2.1 Faust关系式(1)Faust给出了速度、年代和深度的关系式如下:
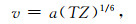
|
(1) |
式中,v是地层层速度,T是地层年龄,Z代表地层深度,a为常数.当速度单位为ft/s(1 ft=0.3048m),年龄单位为年,深度单位为ft,a=125.3;当速度单位为m/s,深度单位为m,a=46.5[3].显然,对某一盆地(面积不是很大),且是连续沉积、没有沉积间断,以砂泥岩为主的沉积岩,上述关系式可能是对的.
(2)但对中国,大地构造错综复杂,特别是塔里木盆地,地层从元古界到第三系均有沉积,且有多个不整合面,大的构造运动对盆地的不同地区有不同响应,而且又有大量碳酸岩盐沉积,在这种情况下,这个公式便不能适用,即使文献[1]作了温度校正.
(3)另外,Faust曾谈到,如果年龄测定用14C同位素,结果将使定量关系式中的参数更准确.需要注意的是14C同位素定年由于其半衰期小,14C法能测定几千~几万年的地质样品,如考古、黄土等学科常用14C法.而一般地质定年则常用U-Pb、Pb-Pb、K-Ar、Rb-Sr、Sm-Nd、Re-Os等方法[9~11],通常不用14C法.
(4)重要的是,Faust的公式中地震波速度v与地层年龄T关系是经验的,并没有必然的成因关系.从宏观上,地层的压实作用使砂泥岩的孔隙度、渗透度的变化在地震波速上有所响应,但是如果砂泥岩地层经受了不同的热液作用,使砂泥岩发生硅化,方解石化、白云石化、绿泥石化等等,则使上述公式多了一些不确定性,而这种热液蚀变作用在一些沉积盆地中是经常发生的.
2.2 关于盆地基岩的年龄与地震波速的关系关于盆地基岩情况便更复杂:①盆地基底岩石可以由不同种类的岩石组成,如花岗岩、火山岩及各种类型的变质岩,不同的基岩地震波速是不同的;②盆地基底是起伏的,其深度是不同的;③通常盆地基底与上覆沉积岩有一个很大的沉积间断,即有一个不整合面,因此,利用上述公式计算基底的年龄便有更大的不确定性.
3 地球物理定年与实测年龄的比较文献[1]对式(1)作了温度校正等改进,获得了一个适合中国大陆沉积盆地的速度、深度和年龄的定量表达式[1],即
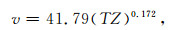
|
(2) |
经过变换,获得地球物理定年的时间表达式即为
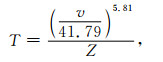
|
(3) |
以下看看利用式(3)所计算的年龄与实测年龄的关系.
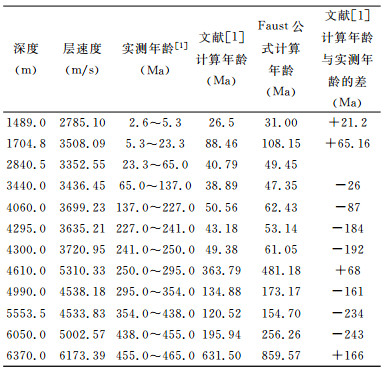
3.1 塔里木盆地某口井(1489~6370m)的年龄表 1为塔里木盆地某口井的计算年龄与实测年龄的比较.
|
|
表 1 某井计算和实测年龄比较 Table 1 Comparison of computational ages and determinated ages in a well |
文献[1]认为,式(3)比式(1)更接近实际年龄数据,可事实是,在这口井的数据中,仅2840m与2840.5m井段的计算年龄值与实测年龄值比较一致,其它11组年龄值均相差很大.按笔者计算,绝对误差为+166~-234 Ma.如此大的差值表明,地球物理定年方法是不可信的.
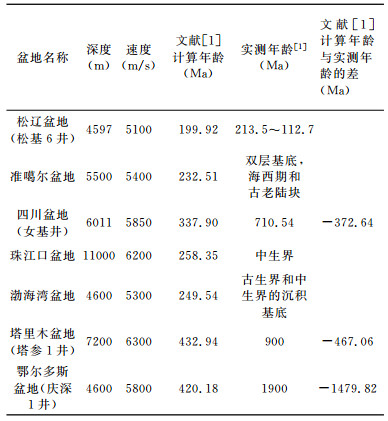
3.2 沉积盆地基底年龄文献[1]用式(3)计算了中国7大沉积盆地基底的年龄(表 2).
|
|
表 2 沉积盆地基底计算年龄与实测年龄对比 Table 2 Comparison of computational ages and determinated ages on sedimentary basins |
从表 2可以看出:①松辽盆地松基6井4597m的基底计算年龄与实测年龄大体相当.②准噶尔盆地5500 m基底计算年代与实测年龄可分两种情况:若基底为海西期的褶皱基底则差值不大,若是古老陆块则差值很大.③珠江口盆地11000 m深的计算年龄为58.35 Ma,文献[1]称11000 m的实测年龄为中生界,事实上目前中国尚没有钻探到10000m以下的深井,这里的中生界应该是根据地震剖面解释而预测的.④渤海湾盆地4600 m的计算年龄为49.54 Ma,如果基底是中生界,则差别不大,但渤海湾盆地的基底大多为古生界、元古界还有太古界,如果这样,则计算年龄与实际年龄差别就太大了.⑤表 2中还有3个克拉通盆地(四川盆地、塔里木盆地、鄂尔多斯盆地)它们的基底大多为元古界乃至太古界,因此计算年龄与实测年龄的绝对误差就十分大了,由表 2可知,其差值分别为372.64 Ma、467.06 Ma、1479.82 Ma.
面对上述情况:文献[1]认为:“用所给出的公式大体可以计算盆地基底的年代”.笔者以为这种计算方法是不合理的,没有实质性的依据.
4 结语中国大陆及海上沉积盆地的地震波速度与地层年龄之间缺乏内在成因的联系,由此利用地震波速度计算的地层年龄与实测年龄误差太大,没有任何意义;利用地震波速度计算盆地基底的年龄由于有太多的不确定性,计算的年龄与实测年龄误差更大,没有地质意义.
| [1] | 郭桂红, 郝重涛, 石双虎, 等. 沉积盆地中地震波速度与地层年代的关系. 地球物理学报 , 2009, 52(7): 1793–1799. Guo G H, Hao C T, Shi S H, et al. The relationship between seismic wave velocity and geologic time in sedimentary basin. Chinese J.Geophys (in Chinese) , 2009, 52(7): 1793-1799. |
| [2] | Weatherby B B, Faust L Y. Influence of geological factors on longitudinal seismic velocities. Bulletin A A P G , 1935, 19(1): 1-8. |
| [3] | Faust L Y. Seismic velocity as a function of depth and geologic time. Geophysics , 1951, 16(2): 192-206. DOI:10.1190/1.1437658 |
| [4] | Faust L Y. A velocity function including lithologic variation. Geophysics , 1953, 18(3): 586-597. |
| [5] | Baskell N A. The relation between depth, lithology and seismic wave velocity in Tertiary sandstones and shales. Geophysics , 1941, 6: 318-326. DOI:10.1190/1.1443729 |
| [6] | Stulken E J. Seismic velocities in the southeastern San Joaquin Valley of California. Geophysics , 1941: 62327-355. |
| [7] | Acheson C H. Time-depth and velocity-depth relations in western Canada. Geophysics , 1963, 28(5): 894-909. DOI:10.1190/1.1439292 |
| [8] | 郭桂红, 韩锋. 地质定年方法综述与地球物理定年. 地球物理学进展 , 2007, 22(1): 87–94. Guo G H, Han F. The overview of dating methods and the geophysical dating. Progress in Geophysics (in Chinese) , 2007, 22(1): 87-94. |
| [9] | 朱炳泉. 固体地球科学的同位素体系理论. 北京: 科学出版社, 1998 : 321 . Zhu B Q. Isotopic System Theory in the Solid Geoscience (in Chinese). Beijing: Science Press, 1998 : 321 . |
| [10] | 业渝光. 地质年代学理论与实践. 北京: 地质出版社, 2003 : 1 -383. Ye Y G. The Theory and Parctice of Geochronology (in Chinese). Beijing: Geological Publishing House, 2003 : 1 -383. |
| [11] | 赵俊峰, 刘池洋. 定年的非生物地层学方法. 新疆石油地质 , 2006, 27(6): 757–762. Zhao J F, Liu C Y. Non-biostratigraphical methods for dating. Xinjiang Petroleum Geology (in Chinese) , 2006, 27(6): 757-762. |
 2010, Vol. 53
2010, Vol. 53