人工源大功率电磁技术是利用很强的人工发射信号,探测地下深至10km左右范围内电性细结构的新方法,是地球物理学和无线电物理学相结合的产物[1~6].它在具有一定厚度高阻层的地区铺设超长发射电极距(几十公里)的电缆,大功率(大于500kW)发射0.1~300 Hz的电磁波1),在数千公里范围内接收该电磁信号以达到深部探测的目的.该技术的特点是信号强度大,抗干扰能力强,信号稳定,测量误差小,覆盖范围广,可配多部接收机大面积组网同时观测,避免了现有天然源大地电磁法(MT)接收信号弱、易受干扰的缺点,同时又克服了人工可控源音频电磁法(CSAMT)设备笨重、探测深度浅(1~2km)、覆盖范围小的不足,是MT和CSAMT方法的改进[1~6].
1)国家圣彼得保大学文森-列辛克地壳研究所编写.地球物理研究及地震预测研究中发射-测量装置的发射系统安装场地选择的技术要求及建议.
如果将固体地球表面以上的半空间称作上半空间,以下的半空间称作下半空间.电磁波在下半空间的传播特征已有一系列文章发表[7~13],在这些文章中,电离层和空气层位移电流的影响被忽略,场的分布主要分为近场和远场.在上半空间内,电磁波传播也有一系列文章发表[13~28],但其目的是研究无线电波的传播及通讯问题,在计算场强的时候采用了近似公式,而且研究较多的是电场的垂直分量Ez,该分量虽然在地-电离层波导中传播时衰减小,但与地球及电离层的参数关系不大,关于地球内部的信息量提供的也少.电磁场的其他分量含有更多的大地信息,应该详细地研究它们随地球性质及地球构造特性而变化的规律.
近年来,国内开始了“地-电离层”模式长发射距大功率可控源电磁波传播研究,即考虑电离层-大气层-固体地球层耦合情况下的传播的研究[1~6, 28, 29].由于许多观测点的收发距已经接近或大于电离层高度,在大收发距地区如波导区,由于电离层的影响,电磁场的衰减明显小于不考虑电离层影响的远场电磁波的衰减,辐射极化特征也有差异.但没有给出空气层中位移电流对电磁场的影响.
本文根据研究对象和问题建立“地-电离层”模式水平电缆接地偶极源电磁波场的地质模型和数学模型,所建立的模型不但考虑了电离层的影响,还考虑了空气层中位移电流的影响.对“地-电离层”模式层状介质模型详细推导了电偶极源的电磁波响应.目前关于水平层状大地上电偶极源形成的电磁场公式推导的方法主要有R函数法和层矩阵法,其中R函数法由H.B利普斯卡娅于1969年提出[30],具有物理意义明确、推导简单的优点,被广泛应用于CSAMT的公式推导,国内外有关电磁法的书中多有引用[30~34].因此公式推导采用R函数法,按照推导的公式编排了程序,进行了数值计算,计算了“地-电离层”模式电磁波场随距离的衰减、频率依赖特征等,并和似稳场的结果进行了对比,计算结果中对比了是否考虑空气层中位移电流的差异,它们在高频段由于空气中位移电流的影响而不一样.为进一步开展“地-电离层”模式电磁波场理论进行地下资源探测研究提供了基础.
2 模型的建立及公式推导 2.1 模型的建立建立的模型如图 1所示.电离层设为第-1层,空气层为0层,源放置在空气层中,距离地表高度为h0.坐标系的原点设置在源的中心点正下方的地表,z向下为正,向上为负,故电离层的高度为负数.假设电离层和地球层的最底层的厚度为无限.
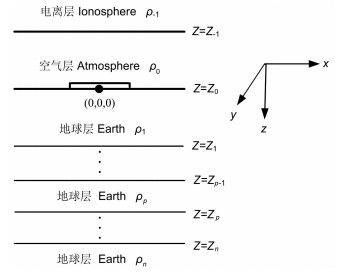
|
图 1 “地-电离层”模型示意图 Fig. 1 The sketch map of "earth-ionosphere" mode |
模型中电离层底界面的有效高度,也就是空气层的厚度为100km,电离层的有效电阻率取为1× 104 Ωm1).每一层的相对介电常数ε和相对磁导率μ均设为1.
2.2 公式推导在距离地表h0高度处放置一水平电偶源,供以谐变电流
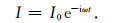
|
(1) |
引入矢量位A后,其基本方程为
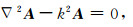
|
(2a) |

|
(2b) |
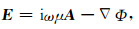
|
(2c) |
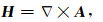
|
(2d) |
式中:A为矢量位;E表示电场矢量;H表示磁场矢量;μ为磁导率,i表示纯虚数;ω为圆频率;k2=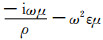
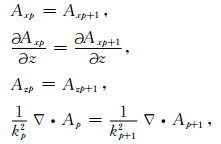
|
(3) |
式中p=-1,0,1,…,n-1,为各层层序.经过一系列推导,可求得Ax,Az
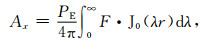
|
(4) |

|
(5) |
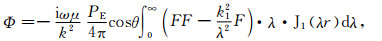
|
(6) |
其中
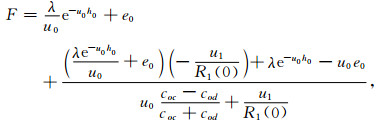
|
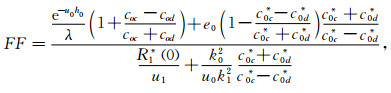
|
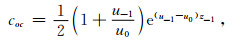
|
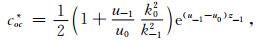
|
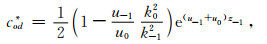
|
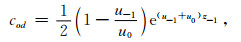
|
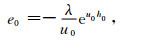
|
式中,u2 p=λ+k2 p;λ为空间频率;kp是第p层的波数;θ为收发距与x轴的夹角;PE=Idl,I为发射电流,dl为偶极长度;r为收发距,即观测点距偶极子中心的距离;J1(λr)、J0(λr)分别是以λr为变量的一阶、零阶贝塞尔函数;R1和R* 1为联系各层物性的两个函数,它们和各个电性层的电导率、层厚有关,它们在地表的具体表达式如下:
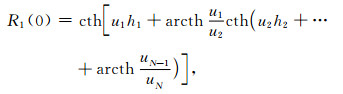
|
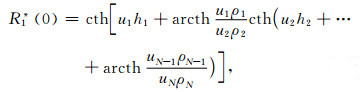
|
(7) |
(7)式中,hp=zp-zp-1,为第p层的厚度,ρp为第p层的电阻率.
本文虽然是考虑了电离层的影响,但R函数是由最底层向上推导的,所以推导过程和CSAMT是一致的[30, 32~34],本文R函数在地表的表达式也与CSAMT一致.
由(2b)式可求得
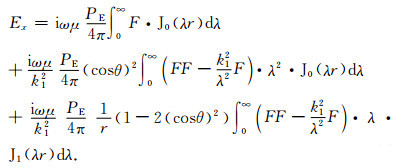
|
(8) |
由(2c)式可求得
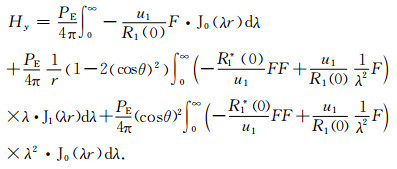
|
(9) |
“地-电离层”模式和CSAMT的场强计算公式的主要差异在系数cod和cod*,它们体现了电离层对场强的影响.如果不考虑电离层和空气中位移电流的影响,同时,将空气层的波数k0=0,这时cod和cod*等于0,(8)式和(9)式经过化简后,和CSAMT的计算公式[30, 32~34]是一样的.
3 数值模拟结果 3.1 数值模拟可行性验证首先应用小尺度模型来检验公式推导和程序计算的正确性和可靠性,对比了“地-电离层”模式三层模型、均匀半空间的数值解和均匀半空间解析解的计算结果.
“地-电离层”模式和均匀半空间数值解均采用Hankel滤波方法[30, 33].均匀半空间解析解的计算公式如下[30]:
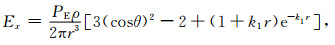
|
(10) |
(10)、(11)式中,ρ为均匀大地电阻率;k1为均匀大地的波数;I0、I1、K0、K1分别是以ik1r/2为变量的零阶、一阶,第一类、第二类修正贝塞尔函数.
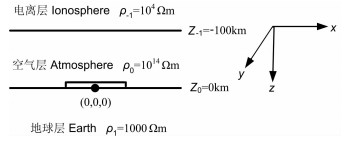
“地-电离层”模式三层模型如图 2所示,均匀半空间模型只考虑地球层.所用频率f=2n,n取值从-6到13,间隔0.5,共39个频点;发射电流I=10A;偶极子AB的长度2L=2km,计算时简化为电偶极子.计算了收发距r为10km时赤道和轴向两种情况,接收点的坐标分别为(x1,y1,z1)=(0km,10km,0km),(x2,y2,z2)=(10km,0km,0km).
|
图 2 “地-电离层”模式三层模型示意图 Fig. 2 The three layers sketch map of "earth-ionosphere" mode |
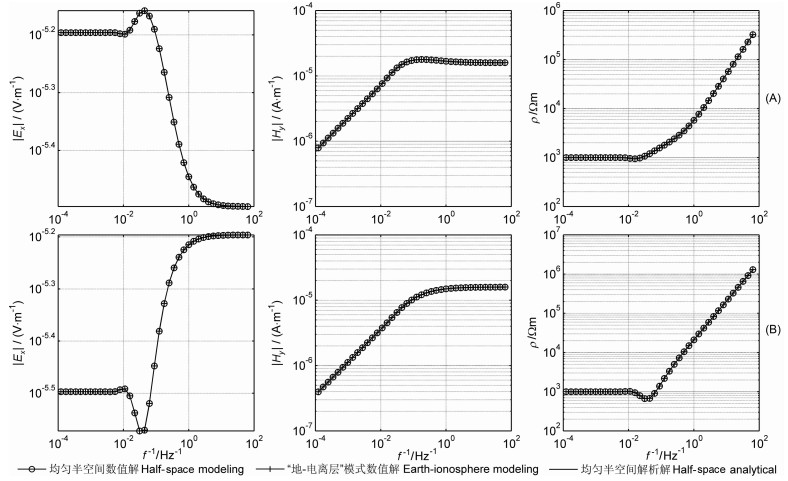
“地-电离层”模式、均匀半空间数值解和均匀半空间解析解的计算结果如图 3所示.图中带“o”标志的曲线为均匀半空间数值解,带“+”标志的曲线为“地-电离层”模式的数值解,实线为均匀半空间解析解.可以看出在收发距只有10km时,它们的计算完全一致.
|
图 3 收发距r为10 km时“地-电离层”、半空间数值解和半空间解析解场强和电阻率的频率响应曲线 (A)赤道装置;(B)轴向装置. Fig. 3 The comparison of |Ex|、|Hy| and ρ for "earth-ionosphere" and half space modeling and half space analytical results with r=10 km (A) Equatorial array; (B) Axial array. |
由于小尺度情况下电离层的影响还没有显现出来,空气中位移电流的影响也很微弱,这时“地-电离层”模式、均匀半空间的数值解和均匀半空间解析解的计算结果不应该有差异,图 3证实了这一点,也就是说进行的公式推导和程序编制以及数值模拟结果是可靠的,可以应用于“地-电离层”模式的数值模拟.
3.2 “地-电离层”模式三层介质大尺度有源场特征 3.2.1 “地-电离层”模式三层模型给定频率波场结构特征为认识“地-电离层”模式近场、过渡场和波导区的电磁场特征,进行了将图 2中大地电阻率改为5000Ωm的“地-电离层”模式轴向和赤道装置的电磁波随距离衰减特征的数值模拟.
定义电离层为介质-1,空气层为介质0,地球为介质1.模型电阻率分别为ρ-1=104Ωm、ρ0=1014Ωm、ρ1=5×103 Ωm.各层的厚度h-1=∞、h0=100km、h1=∞.AB的长度为50km,发射电流I为200A,计算时简化为电偶极子.发射频率f为0.1,5,300Hz.
测量点位于地表,收发距r分别为35,40,50,70,90,100,200,400,800,1600,2500km.
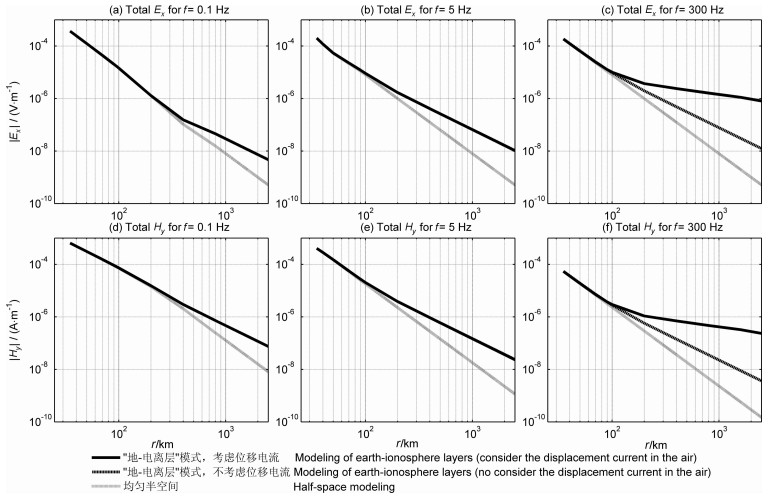
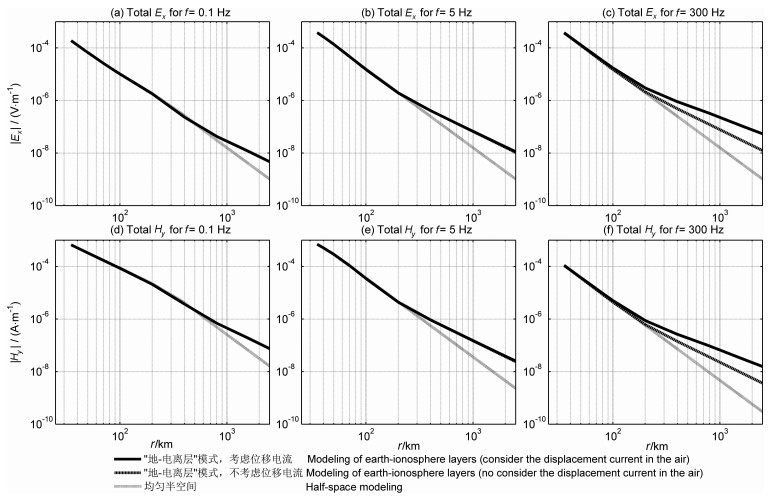
图 4展示了频率分别为0.1 Hz,5 Hz和300 Hz的轴向装置的Ex和Hy场的衰减曲线.图中横坐标为收发距,纵坐标为场强幅值.用实线表示“地-电离层”模式数值模拟曲线(考虑空气层的位移电流),虚线为“地-电离层”模式数值模拟曲线(不考虑空气层的位移电流),点线为解析计算的均匀半空间地球介质似稳场(即不考虑电离层和空气层中位移电流)的衰减曲线.图 4和图 5的结果清楚地表明,无论Ex还是Hy当距离场源较近时,在不考虑电离层及空气层位移电流影响的似稳场情况下,计算所得的曲线(点线)、考虑电离层但不考虑空气层位移电流(虚线)与同时考虑电离层和空气层位移电流影响的曲线(实线)是吻合的.电离层对电磁波场在远距离处有明显的影响,它们的曲线不再吻合,而且考虑空气层位移电流的比不考虑空气层位移电流的场值要大.随着频率的增加,这种差异在更近的距离表现出来.轴向装置(图 4)的差异表现得更明显,它反映了该场源极化方向图的变化.
|
图 4 频率分别为0.1 Hz, 5 Hz和300 Hz的轴向装置的Ex和Hy场的衰减曲线 Fig. 4 Ex and Hy field decay curves for axial array with frequencies 0.1 Hz, 5 Hz and 300 Hz |
|
图 5 频率分别为0.1Hz, 5 Hz和300 Hz的赤道装置的Ex和Hy场的衰减曲线 Fig. 5 Ex and Hy field decay curves for equatorial array with frequencies 0.1 Hz, 5 Hz and 300 Hz |
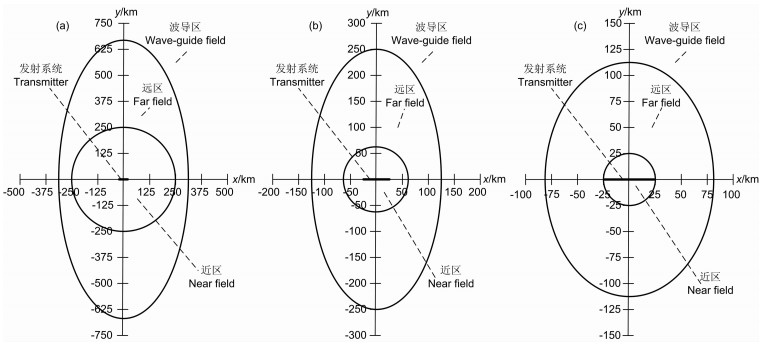
波导区的边界取决于场源的参数、地层以及电离层的性质.我们来分析当采用3.2.1节给定的场源、地层以及电离层的参数时,对近区、远区和波导区的划分.
我们来这样确定波导区的边界1),即似稳场和波导场的|Ex|和|Hy|分量的振幅相差10%,也就是波导场的|Ex|和|Hy|除以似稳场的|Ex|和|Hy|大于等于1.1时就认为进入了波导区.近场和远场的划分,参考文献[34]中的CSAMT远场定义,当r大于3~5倍趋肤深度δ时认为进入远场.但本文中的发射电缆源长度达50 km,所以当CSAMT中关于远场划分计算所得的距离小于25km时,就认为在25km处进入远场. 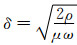
根据计算得到的近场、远场和波导场的划分示意图如图 6.频率越低进入波导区的距离越远,例如0.1Hz时,轴向到310km,赤道方向到675km以远才能进入波导区;300 Hz时,轴向到110km,赤道方向到80km以远进入波导区,这与图 4和图 5所展示的结果是对应的.
有关近场和远场的讨论,可以参阅有关CSAMT的文献[30~32].
|
图 6 近区、远区及波导区的边界 (a)f=0.1Hz;(b)f=5Hz;(c)f=300Hz Fig. 6 The boundary of near, far and wave-guide field |
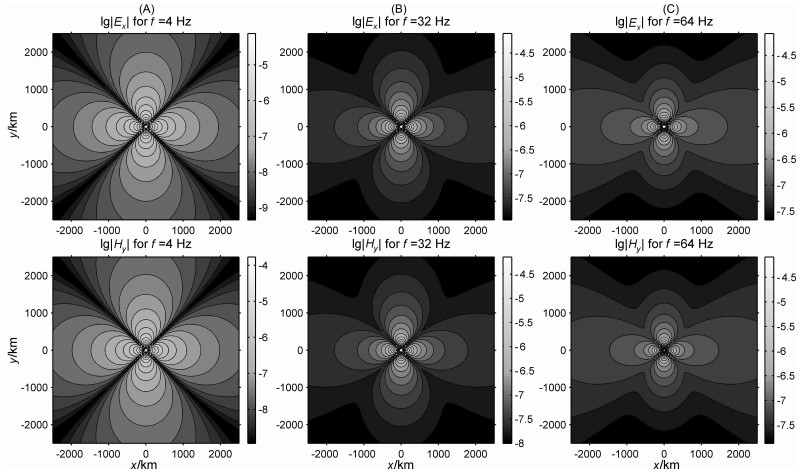
为了更好地理解图 4~图 6的计算结果,我们采用3.2.1节中的模型,计算了“地-电离层”模式4Hz、32Hz和64Hz的辐射花样,计算结果见图 7.
|
图 7 “地-电离层”模式辐射花样 (A)/=4 Hz;(B)32 Hz;(C)/=64 Hz. Fig. 7 "Earth-Ionosphere" mode radiation pattern |
从辐射花样可以看出,频率为4 Hz时,电磁场在赤道和轴向方向的衰减没有明显差异;频率为32Hz时,两个方向的衰减出现了明显的差异,轴向方向的衰减更小,导致出现了场源方向图的变化,特别是收发距大了之后,变化明显;频率为64Hz时场源方向图发生变化很明显,并随着距离的增加而越发明显,这种变化在高频时轴向的衰减相对赤道要慢很多,这是由于电离层和空气层位移电流共同作用的结果.
由图 4~图 7可以得出,对于可作用于数百~数千公里外的场源,要划分出一个额外的波导区,在这个区电磁场分量与远区相比有许多不同的特征.这些不同点主要体现在:(1)场源的方向图发生变化;(2)有利于测量阻抗Zxy和Zyx的区域的相对位置发生了变化;(3)场源的方向图发生变化是随频率越高变化越明显.
3.2.4 “地-电离层”模式中考虑位移电流的必要性分析为解释3.2.1节和3.2.2节中计算结果是否考虑位移电流的差异,我们来分析位于均匀半空间表面上水平电偶极子考虑空气层位移电流磁场的垂直分量的解析表达式[30]:
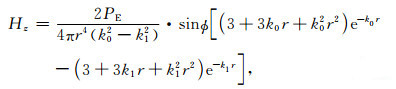
|
(12) |
式中,PE为偶极子的极矩,等于电流强度I和发射源长度dl的乘积;r为收发距;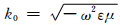
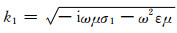
当k0r≪1和k1r≪1(小极距,低频率)时,式(12)可以简化成如下形式:
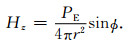
|
(13) |
在小极距、低频率范围内水平电偶极子的垂直磁场与下半空间的导电性无关,只是一次场随着频率的降低和距离的增加而衰减.
(12)式中第二项指数项描述的是地球介质对电磁场能量的吸收,在高频段当k1r≫1时,它趋于零,对于波导区其表达式为
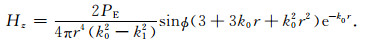
|
(14) |
在分析式(14)时,可以认为空气中的波长比收发距要大,这样指数中的乘积项可以忽略,使得指数的值趋于1.下一步是对k02-k12进行分析.
在实际工作中一般采用的频段为f < 105 Hz,电阻率ρ≤105 Ωm,εω≪iσ,因此k02≪k12.所以在研究中可以忽略介电常数(即位移电流)的影响,除非研究的深度非常小(地表浅部几米),此时采用的频率为106~108 Hz或更高.这种假设称之为似稳定近似.在正演过程中,这种假设被广泛采用,以简化计算过程.
从上面的讨论可以看出,采用似稳定近似不仅受到高频方面的限制,而且受到大极距方面的限制.当极距与空气中波长存在可比性时,由于值k0r=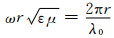
所以在进行“地-电离层”模型正演计算时,必须考虑空气层中位移电流的影响.这也可以解释图 4、5中,关于“地-电离层”模型的计算结果,是否考虑空气层中位移电流的差异.
4 结论本文进行了“地-电离层”模式大功率可控源的电磁波正演研究.建立了“地-电离层”模式层状地球表面水平电偶源形成的谐变场的地质和数学模型,利用R函数法进行了“地-电离层”模式的公式推导,得出“地-电离层”模式地球表面水平电偶源的场强表达式.
通过数值计算给出了“地-电离层”模式三层模型不同频率、不同收发距的轴向和赤道装置的(似稳定场、是否考虑空气中位移电流的)场强衰减对比图,辐射花样,近区、远区、波导区的边界图以及波场的频率特征图.
数值模拟结果表明,本文的计算结果与文献[1]中的结果在高频段有较大的差异,原因是文献[1]没有考虑空气中位移电流的影响.文中的理论分析部分已经得出结论,必须考虑空气中位移电流的影响.
空气中位移电流的影响随着收发距的增大,在更低的频率上体现出来,主要表现为Ex和Hy随着频率的增加而增加,收发距越大,Ex和Hy随频率的增加就越快,而且这种场强随频率增加而增加的现象轴向装置要比赤道装置更明显.
对于可作用于数百~数千公里外电磁场观测的大功率场源,电磁场受到电离层和空气中位移电流的影响,要划分出一个额外的波导区,在波导区电磁场分量与远区相比有许多不同的特征.这些不同点主要体现在:(1)电磁场分量的振幅值因电离层的存在而衰减得更慢,而且考虑位移电流比不考虑位移电流衰减更慢,衰减程度随频率增加而增加;(2)场源的方向图发生变化;(3)有利于测量阻抗Zxy和Zyx的区域的相对位置发生了变化.
本文的计算是将发射源假设为电偶极子,这样的假设在收发距很大时是可行的,但在距离场源不远时应该对近场和远场采用有限长导线积分方法进行求解.下一步的工作研究“地-电离层”电磁波的各种地电模型的响应特征,以便为该方法的实际应用提供更多的基础.
| [1] | 底青云, 王妙月, 王若, 等. 长偶极大功率可控源电磁波响应特征研究. 地球物理学报 , 2008, 51(6): 1917–1928. Di Q Y, Wang M Y, Wang R, et al. Study of the long bipole and large power electromagnetic field. Chinese J.Geophy. (in Chinese) , 2008, 51(6): 1917-1928. |
| [2] | 底青云, 王光杰, 王妙月, 等. 长偶极大功率可控源激励下目标体电性参数的频率响应. 地球物理学报 , 2009, 52(1): 275–280. Di Q Y, Wang G J, Wang M Y, et al. Frequency response characteristics of target electric property with long bipole large power control source. Chinese J.Geophys. (in Chinese) , 2009, 52(1): 275-280. |
| [3] | 赵国泽, 汤吉, 邓前辉, 等. 人工源超低频电磁波技术及其用于首都圈地震预测的测量研究. 地学前缘 , 2003, 10(Suppl.): 248–257. Zhao G Z, Tang J, Deng Q H, et al. Artificial SLF method and the experimental study for earthquake monitoring in Beijing area. Earth Science Frontiers (in Chinese) , 2003, 10(Suppl.): 248-257. |
| [4] | 赵国泽, 陆建勋. 利用人工源超低频电磁波监测地震的试验和分析. 中国工程科学 , 2003, 5(10): 27–33. ghao G Z, Lu J X. Monitoring & analysis of earthquake phenomena by artificial SLF waves. Engineering Sciences (in Chinese) , 2003, 5(10): 27-33. |
| [5] | 卓贤军, 赵国泽. 一种新的资源探测人工源电磁技术. 石油地球物理勘探 , 2004, 39(Suppl.): 114–117. Zhuo X J, Zhao G Z. A new technique of EM controlled-source sounding for resource prospecting. Oil Geophys.Prosp. (in Chinese) , 2004, 39(Suppl.): 114-117. |
| [6] | 陈小斌, 赵国泽. 关于人工源极低频电磁波发射源的讨论-均匀空间交流点电流源的解. 地球物理学报 , 2009, 52(8): 2158–2164. Chen X B, Zhao G Z. Study on the transmitting mechanism of CSELF waves:response of the alternating current point source in the uniform space. Chinese J.Geophys. (in Chinese) , 2009, 52(8): 2158-2164. |
| [7] | 底青云, MartynUnsworth, 王妙月. 复杂介质有限元2. 5维可控源音频大地电磁法数值模拟.地球物理学报 , 2004, 47(4): 723–730. Di Q Y, Unsworth M, Wang M Y. 2.5D CSAMT modeling with the finite element method over 2D complex earth media. Chinese J.Geophys. (in Chinese) , 2004, 47(4): 723-730. |
| [8] | 汤井田, 罗维斌, 刘长生. 海底油气藏地质模型的冲激响应. 地球物理学报 , 2008, 50(6): 1929–1935. Tang J T, Luo W B, Liu C S. Impulse response of seafloor hydrocarbon reservoir model. Chinese J.Geophys. (in Chinese) , 2008, 50(6): 1929-1935. |
| [9] | 薛国强, 李貅. 瞬变电磁隧道超前预报成像技术. 地球物理学报 , 2008, 51(3): 894–900. Xue G Q, Li X. The technology of TEM tunnel prediction imaging. Chinese J.Geoph ys. (in Chinese) , 2008, 51(3): 894-900. |
| [10] | 郑圣谈, 曾昭发, 刘四新, 等. 宽带高频电磁场数据反演方法研究. 地球物理学报 , 2008, 50(1): 266–272. Zheng S T, Zeng Z F, Liu S X, et al. Inversion of the wideband and high frequency electromagnetic data. Chinese J.Geophys. (in Chinese) , 2008, 50(1): 266-272. |
| [11] | 陈小斌, 赵国泽, 汤吉, 等. 网式大地电磁阻抗张量及其影响因素分析. 地球物理学报 , 2008, 50(1): 273–279. Chen X B, Zhao G Z, Tang J, et al. Impedance tensor of network-MT and the influencing factors. Chinese J.Geophys. (in Chinese) , 2008, 50(1): 273-279. |
| [12] | 王若, 王妙月, 底青云. 频率域线源大地电磁法有限元正演模拟. 地球物理学报 , 2006, 49(6): 1858–1866. Wang R, Wang M Y, Di Q Y. Electromagnetic modeling due to line source in frequency domain using finite element method. Chinese J.Geophys. (in Chinese) , 2006, 49(6): 1858-1866. |
| [13] | 刘长胜, 林君. 海底表面磁源瞬变响应建模及海水影响分析. 地球物理学报 , 2006, 49(6): 1891–1898. Liu C S, Lin J. Transient electromagnetic response modeling of magnetic source on seafloor and the analysis of seawater effect. Chinese J.Geophys. (in Chinese) , 2006, 49(6): 1891-1898. |
| [14] | Barr R, Jones D L, Rodger C J. ELF and VLF radio waves. Journal of Atmospheric and Solar-Terrestrial Physics , 2000, 62(17): 1689-1718. |
| [15] | Mushtak V C, Williams E R. ELF propagation parameters for uniform models of the earth-ionosphere waveguide. Journal of Atmosphere and Solar-Terrestrial Physics , 2002, 62(18): 1989-2001. |
| [16] | Wait J R. Electromagnetic Wave in Stratified Media. Oxford University Press , 1970. |
| [17] | Bannister P, Williams F J. Results of the August 1972 Wisconsin test facility effective earth conductivity measurements. Journal of Geophysical Research , 1974, 79(5): 725-732. DOI:10.1029/JB079i005p00725 |
| [18] | Galejs J. Terrestrial Propagation of Long Electromagnetic Waves. Pergamon Press , 1972. |
| [19] | Bannister P. Some note on ELF earth-ionosphere waveguide daytime propagation parameters. IEEE Antenna and Propagation , 1979, 27(Suppl.): 696-698. |
| [20] | Bannister P. ELF propagation update. Journal of Oceanic Engineering , 1984, 9(3): 179-188. DOI:10.1109/JOE.1984.1145609 |
| [21] | Galejs J. Horizontally oriented antennas in the presence of an anisotropic ground. Radio Science , 1969, 11(4): 1047-1053. |
| [22] | Greifinger C, Greifinger P. Approximate method for determining ELF eigenvaluea in the earth-ionosphere waveguide. Radio Science , 1978, 13(5): 831-837. DOI:10.1029/RS013i005p00831 |
| [23] | Greifinger C, Greifinger P. On the ionosphere parameters which govern high-latitude ELF propagation in the earthionosphere waveguide. Radio Science , 1979, 14: 889-895. DOI:10.1029/RS014i005p00889 |
| [24] | Field E C, Engel R D. The detection of daytime nuclear bursts below 150kin by prompt VLF phase anomalies. Proc.IEEE , 1965, 53(12): 2009-2017. DOI:10.1109/PROC.1965.4477 |
| [25] | Bannister P. Summary of the Wisconsin test facility effective earth conductivity measurements. Radio Science , 1976, 11(4): 405-411. DOI:10.1029/RS011i004p00405 |
| [26] | Bannister P. Far-field Extremely Low Frequency (ELF) propagation measurements, 1970-1972. Communications, IEEE Transactions on , 1974, 22(4): 468-474. DOI:10.1109/TCOM.1974.1092222 |
| [27] | Bannister P. Summary of connecticut 76-Hz vertical electric, transverse magnetic, and radial magnetic field-strengthcomparisons. Radio Science , 1986, 21(3): 519-528. DOI:10.1029/RS021i003p00519 |
| [28] | 李勇, 林品荣, 徐宝利, 等. 电离层影响下均匀半空间水平谐变电偶极子的电磁响应计算. 物探化探计算技术 , 2008, 30(6): 500–505. Li Y, Lin P R, Xu B L, et al. Computing the electromagnetic response of the time-harmonic horizontal electric dipole in a homogenous half-space under ionosphere coupling. Computing Techniques for Geophysical and Geochemical Exploration (in Chinese) , 2008, 30(6): 500-505. |
| [29] | 王元新, 彭茜, 潘威炎, 等. SLF/ELF水平电偶极子在地一电离层波导中的场. 电波科学学报 , 2007, 22(5): 728–734. Wang Y X, Peng Q, Pan W Y, et al. The fields excited by SLF/ELF horizontal electric dipole in Earth-ionosphere cavity. Chinese Journal of Radio Science (in Chinese) , 2007, 22(5): 728-734. |
| [30] | 朴化荣. 电磁测深法原理. 北京: 地质出版社, 1990 . Piao H R. The Principle of Electromagnetic Sounding (in Chinese). Beijing: Geological Publishing House., 1990 . |
| [31] | 陈乐寿, 王光锷. 大地电磁测深法. 北京: 地质出版社, 1990 . Chen L S, Wang G E. Electromagnetotelluric method (in Chinese). Beijing: Geologieal Publishing House, 1990 . |
| [32] | 何继善编译.可控源音频大地电磁法.长沙:中南工业大学出版社, 1990 He J S.Controlled Source Audio Frequency Magnetotellurics Method (in Chinese).Changsha:Central South University of Technology Press, 1990 |
| [33] | 汤井田, 何继善著.可控源音频大地电磁法及其应用.长沙:中南大学出版社, 2005 Tang J T, He J S.Controlled Source Electromagnetic Method and Its Applications (in Chinese).Changsha:Central South University Press, 2005 |
| [34] | 底青云, 王若. 可控源音频大地电磁数据正反演及方法应用. 北京: 科学出版社, 2008 . Di Q Y, Wang R. CSAMT Forward Modeling and Inversion and Its Application (in Chinese). Beijing: Science Press, 2008 . |
 2010, Vol. 53
2010, Vol. 53

