随着水声技术的发展,已有越来越多的声纳设备应用于沉底目标或掩埋目标的探测[1, 2],由此也推动了对海底界面附近目标声散射的研究工作[3, 4]。界面附近目标的声散射不仅是声纳探测的研究内容,也是医学成像、地质勘探和无损检测的重要研究内容之一。
海底界面附近目标的声散射建模一方面是检验相关理论的前提,另一方面也是实际测量数据处理和分析的基础。利用某些数值方法可以实现声散射建模,例如,结合有限元模型和虚源近似法的OASES-3D建模软件[5],以及基于有限差分数值计算方法的海底掩埋目标声波散射建模[6]等。然而,这类方法很难对其声场计算结果给出明确的物理解释,另外,对于此类无限界面和有限目标系统的声散射,还需要考虑计算效率等问题。T矩阵(Transition matrix)方法[7, 8]是由惠更斯原理引申出的一种数值积分方程方法,Kristensson和Ström (1978,1980)[9, 10]首先利用该方法研究了界面附近目标的声散射,推导出了两个半无限流体空间之一中含有有界非均匀体的声散射精确公式,并数值计算考察了声源和球体目标位于不同半空间的异常声散射场。为了了解声纳目标与海底界面之间声波相互作用的物理机制,在此基础上Lim等(1993)[11]以半空间水体和流体海底中间夹一任意水平流体过渡层的简化方式建立了掩埋目标的声散射模型,重点数值考察了指向性波束入射时界面和沉积物负载所引起的掩埋球壳反向共振散射结构的变化,并对远距离水中检测掩埋目标的可能性做了分析; 另外,文中还给出了在水池中所进行的大掠射角时掩埋球壳目标散射回波的测量结果,通过比较实验和计算得到的目标反向散射形态函数,初步说明了以T矩阵方法建立模型的可靠性。对于界面和目标系统的声散射问题,T矩阵方法的关键是将入射场和散射场(或反射场)在不同的坐标系中展开,从理论上讲对目标的性质和形状没有限制。由于在处理界面和目标系统声散射问题上的优越性,近年来T矩阵方法也开始用于粗糙海底界面附近目标的声散射理论研究中[12~14]。
鉴于实际海底情况的复杂性,有关沉积物中的声传播规律及其界面的声能透射规律还是当今研究难点,因此,掩埋目标的声散射建模及其实验研究存在许多机理问题有待解释[15]。最近,在Acoustic08巴黎会议[16]上进行了“界面附近目标声散射”的专题交流,所讨论的主题是界面附近目标的声散射机理的解释和验证,其中有更多的工作是对实验室便于测量和控制的沉底目标(或水面附近目标)的声散射规律及其建模的研究。从T矩阵方法研究的角度看,海底全掩埋目标与位于海底上方目标的声散射属于同一类问题。Bishop和Smith (1999)[17]在他们提出的流-固粗糙界面与弹性壳体声散射理论[12]的基础上,研究了平面上方流体中刚性和软性目标的声散射建模,其特点是利用直角坐标系中的基函数获得目标存在时界面声散射的T矩阵,因此该模型仅适于对平面波入射情况的计算。Fawcett等(1998)[18]在Lim等[11]模型的基础上探讨了平面海底界面上柱体和球体目标的反向散射强度模拟实现问题,将球坐标系中基函数展开的散射场做单次散射近似提高了计算效率,通过计算得到的与全多极散射场的一致结果证明了该方法的准确性。当选取适于目标或有限体的基坐标系(如球坐标系或柱坐标系)时,界面对入射场和目标散射场的影响将以波数积分的形式表示。为了提高计算效率,Fawcett和Lim (2003)[19]对于目标-海底散射中的积分计算问题,首先引入复像方法[20, 21]研究了散射声场的快速计算,并通过与积分计算结果的比较证明了该方法的准确性。然而,上述的声场计算方法均是针对入射平面波并且数学推导复杂。
本文将在相关的T矩阵方法和复像方法的已有研究基础上,首先推导由点源激发的平面海底界面上方目标的声散射公式,考察利用复像方法进行计算的准确性,然后给出不同入射方向的界面上刚性球体和弹性球壳的散射声场算例,最后给出相关的实验设计及分析与模型的对比结果。
2 界面上方目标的声散射公式T矩阵方法是建立在波动方程基础上的一种散射声场积分表示求解方法[7]。对于自由空间中目标的声散射问题,可以认为空间中任意点的声场是由声源激发的入射场ϕ0和目标激励的散射场ϕs两部分构成。将入射场和散射场展开成适于目标的基函数形式(如三维的球谐函数、二维的柱函数),并根据目标表面的边界条件确定入射场和散射场展开系数之间的关系(即目标的T矩阵表示),最终将以级数和的形式计算散射声场,即

|
(1) |

|
(2) |
式中的展开系数fn与an通过T矩阵有如下关系:
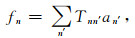
|
(3) |
其中Tnn′是T矩阵之元素,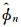
对于占有一定空间的散射体,采用球坐标系r=(R,φ,θ)较为方便,此时入射场(1)式的正则基函数为
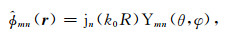
|
(4) |
而(2)式中的向外辐射基函数为
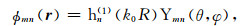
|
(5) |
它们表示声源激发的和目标散射的各阶球谐函数声场,其中jn和hn(1)为n阶球贝塞尔函数,归一化的球谐函数Ymn的表达式为

|
(6) |
Pm n为连带勒让德函数,式中下角标有确定的整数取值范围:-n≤m≤n,0≤n≤∞。显然,式(1)至(3)中对n或n′的求和是指对所有m和n求和的缩写,(3)式中的T矩阵只与目标的几何和声学性质有关。原则上,T矩阵方法适用于具有一般结构的目标,只要满足在所选基坐标系中其T矩阵表示收敛,对于球体(刚性球、弹性球或球壳等),其T矩阵是简单的对角矩阵[22]。
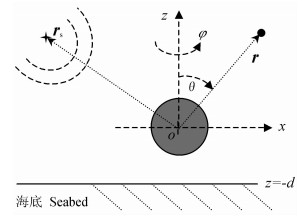
在处理界面附近目标的三维声散射时,为了将描述界面的坐标系与描述目标的坐标系统一,一般考虑将目标散射的基函数(或格林函数)展开成柱面波的形式,从而可以直接利用以平面波确定的界面反射系数。我们将利用复像方法建立以目标坐标系统一描述的平面海底界面上方目标的声散射模型。根据T矩阵的普适性,在此考虑随距离不变的海底上方球体的声散射问题,图 1是描述该问题的示意图。为了研究的方便,假设球体目标的半径为a,其中心选为坐标原点; 海底视为半无限流体介质,海底界面位于目标下方d处,如果取d=a则特殊化为界面上球体的声散射问题。为了接近海底界面附近目标的声波探测实际情况,我们考虑一个位于rs=(Rs,φs,θs)处的点声源,而接收器位于上半空间水体中的r处。
|
图 1 界面上方目标声散射示意图 Fig. 1 The scattering geometry to be modeled |
在自由空间中,由源点rs传播到场点r的球面波可以表示为柱面波叠加的形式(省略时间项e-iωt)[23]:
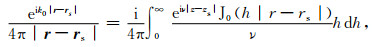
|
(7) |
式中,J0是零阶柱贝塞尔函数,h、ν=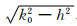
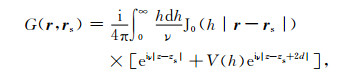
|
(8) |
其中,V(h)为平面声波由半空间水体入射海底界面时的总反射系数,

|
(9) |
其中,ρf和ρ1分别为上下半空间各介质的密度; 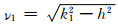

|
(10) |
当q=0时,b0=0、a0=V0,其中V0为反射系数的准静态项:
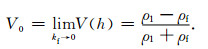
|
(11) |
将(10)式代入(8)式并根据(7)式,可以将半空间的格林函数简化为

|
(12) |
该式即是复像方法[20, 21]的数学描述,它表示界面附近点源激发的声场可以等价为直达场与Q+1个复像激发声场的和。式中,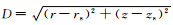

|
(13) |
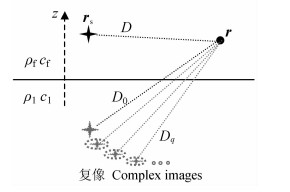
图 2给出了复像方法的解释示意图:界面对其附近点源激发的声场影响可以等价为Q+1个复像激发声场的叠加; 如果界面为刚性或柔性边界,则对应于V=±1的实像,这将退化为通常的虚像方法。注意到反射系数仅依赖于界面上下介质的性质,故(12)式中的系数aq和bq与声源和接收的位置无关,因此以求和代替积分将避免不同位置接收时的重复计算,另外有限项的求和比积分运算更快速便捷。
|
图 2 复像方法解释示意图 Fig. 2 Sketch of the complex images |
根据无限介质空间中点源激发声场的格林函数展开公式[24],并利用上述半空间格林函数的复像表示形式,经过简单推导可以获得对应(1)式中有界面时入射场的展开系数:
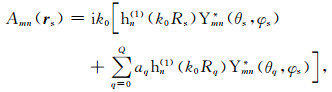
|
(14) |
其中,h(1) n为第一类球汉克尔函数,而
式(14)和(15)说明海底界面对点源的入射声场展开系数等价于多个复像点源入射声场展开系数的叠加。界面的存在同样会影响目标散射场的基函数形式,利用类似的推导,有界面时对应(5)式的向外辐射基函数可以表示为
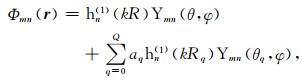
|
(16) |
其中的Rq和θq仍由(15)式确定,只是式中的rs和zs由r和z代替。在Fawcett等[19]的推导中是对积分表示利用复杂的数学关系式而获得(16)式的。
与无限空间中单散射体的情况不同,界面附近的目标将与界面产生多次散射(multiplescattering)。在文献[25]中详细推导了水平分层界面与其中目标的多次散射T矩阵表示,对于本文情况该T矩阵可以表示为
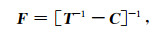
|
(17) |
其中T是目标的自由场T矩阵,C是重散射矩阵,它表示向外辐射球谐函数转化为入射球谐函数的系数,其具体表达式参见文献[19]。将T以F替换,(17)式代入(3)式,并考虑到(14)式,即可确定散射场展开系数为
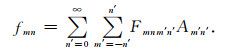
|
(18) |
综合上述对展开系数和基函数的推导结果,最后可以得到接收位置的散射声场:

|
(19) |
为了讨论问题的方便,本文只考虑目标的单次散射近似情况[18],即取(17)式中的C=0(或F=T),此时界面与目标的相互影响已包含在展开系数Amn (rs)和Φmn(r)中。
3 基于复像方法的系数计算如上分析表明,利用复像方法使格林函数的表达式变得非常简单,另外,以有限个复像求和代替积分,使计算效率大大提高。然而,反射系数的展开系数an和bn不能直接获得,还需要利用非线性估计方法确定。利用Prony方法可以由确定的反射系数估计系数an和bn。对于一个给定的随实变量t变化的复函数V(t),Prony方法可以得到如下的近似形式:
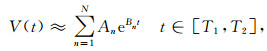
|
(20) |
其中,An和Bn是复系数,[T1,T2]是函数V(t)的定义区间。
在利用(10)式估计系数an和bn之前,首先注意到(9)式中变量ν是一复量,为了利用Prony方法,必须寻找一个实变量t使其与ν保持线性变化关系。另外,反射系数存在支点h=k0和h=k1,为了避免支点附近函数的快速变化,还要避开这些支点。根据Fang等[20]的路径选取方式,假设:
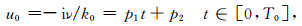
|
(21) |
式中负号是由辐射条件决定,T0是人为选取的正实数,而p1和p2为待定系数。根据积分路径变换中的对应关系,选取(8)式中水平波数的积分上下限分别为hmin=0和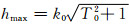
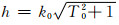
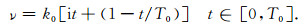
|
(22) |
将(22)式代入(10)式中可以得到:
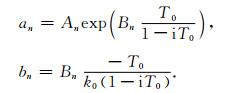
|
(23) |
由此可根据(7)、(13)和(16)式计算格林函数、入射场展开系数和向外辐射基函数。
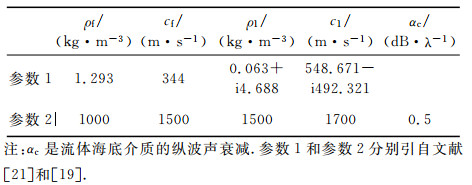
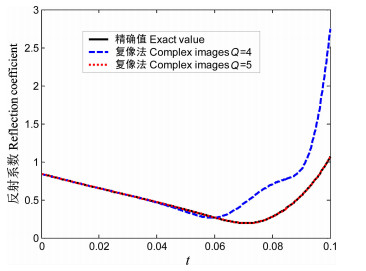
图 3是选取表 1中参数1计算得到的反射系数随变量t的变化。其中实线为由(9)式得到随t变化的反射系数精确值; 断线为选取Q=4(复像个数为5)时拟合得到的反射系数,可以看出在小t处拟合较好,而在大t处拟合效果不好; 利用6个复像(Q=5)的拟合效果图中点线都很好。将各个复像的系数an和bn代入(12)和(13)式将得到半空间格林函数值,如图 4所示。图中给出的是单位强度声源S=1m的声压级L=20lg (p/p0),而声源位于(0,0,1 m)处,1000个接收器均匀分布在(0,0,2 m)和(100 m,0,2m)之间。图中还给出了无限介质中声源的参考值20lgD0。可以看出:Q=5计算得到的结果与通过数值积分计算的结果基本一致,并与文献[21]结果相符。
|
|
表 1 计算中的介质参数 Table 1 Material properties of the media |
|
图 3 反射系数拟合结果(参数1) Fig. 3 The exact and complex-image reflection coefficient |

|
图 4 半空间格林函数 Fig. 4 Green function by integral and complex-image |
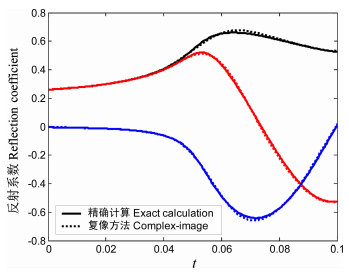
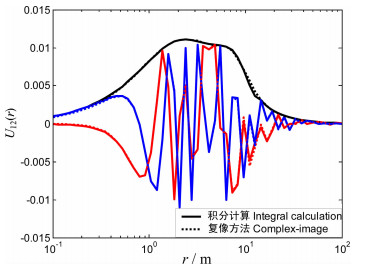
图 5和图 6分别是选取表 1中参数2计算得到的反射系数和文献[19]中定义的向外辐射基函数Umn。在图 5中给出了反射系数的幅度(黑线)、实部(红线)和虚部(蓝线)随变量t的变化,可以看出同样利用6个复像以展开系数得到的反射系数(图中虚线)与真实的反射系数(图中实线)有很好的一致性。在图 6中,实线是通过数值积分得到的向外辐射基函数U12,而虚线是利用复像方法得到的辐射基函数,除了10m范围有小的差别外,其他范围的基函数的幅度(黑线)、实部(红线)和虚部(蓝线)都基本一致。
|
图 5 反射系数拟合结果(参数2) Fig. 5 The exact and complex-image reflection coefficient |
|
图 6 Umn的积分和复像法计算比较(m=1,n=2) Fig. 6 Umn(m=1, n=2) by integral and complex-image |
在球面波展成柱面波叠加形式的积分计算(6)式中,对于不同的发射和接收位置配置都要进行重复的积分运算,而采用复像求和形式的计算公式(6)或(16)式可以利用Matlab中的矩阵或数组运算一次获得不同发射和接收位置的有关函数。另外,依据文献[19]对声衰减随频率线性变化的海底介质可以建立反射系数的展开系数与频率的线性关系,采用复像求和形式可以避免多个频率的重复计算。
4 数值计算结果与分析利用入射场的展开系数(14)式不仅可以用于点源激发目标声散射场的计算,而且,由球汉克尔函数的渐近展开也可以计算平面波入射时散射声场。在文献[21]中,作者直接给出了平面波的入射声场展开系数的表示形式(原文中公式11),其实它是(13)式中忽略Q个复像影响的近似结果。本文仍然选用表 1中参数2数值考察位于rs=50 m处的3kHz点源所激励的位于界面上球体目标的散射声场,接收线列阵水听器位于z=2a、y=0、水平距离x由-5m~5m的范围。为了对不同性质目标的声场进行比较,计算中选取了a=0.25m的刚性球体和具有同样半径的厚度半径比为0.02的弹性球壳(其介质参数为:密度ρ=7900kg/m3,纵波声速cp=5790m/s,横波声速cs=3100m/s,内部真空)。
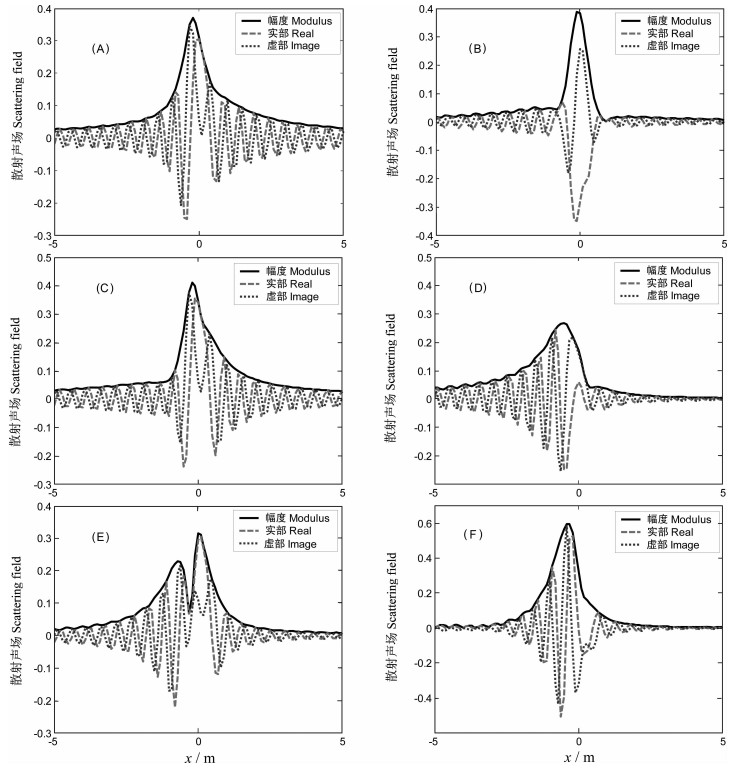
图 7A和7B分别给出了根据(19)式计算得到的入射角度20°时刚性球体和弹性球壳的散射声场(注:其中声场幅度按声源距离做了归一,故可与平面波入射情况比较)。由于本文的计算中考虑了多个复像的影响而忽略目标与界面的多次散射作用,所以与文献[21]中图 4的结果稍有差别。由图 7A中刚性球体散射声场的幅度随水平距离变化可以看出,位于目标附近的声场幅度会有明显的起伏变化,约在x=-0.2 m达到最大。然而对于弹性球壳情况(图 7B),其散射声场幅度显著变化的范围变小而幅度与刚性球体情况相当,最大幅度约位于x=-0.1m处。
|
图 7 刚性球体(A,C,E)与弹性球壳(B,D,F)的散射声场(A,B)20°入射;(C,D)40°入射;(E,F)60°入射. Fig. 7 Scattering field of rigid sphere (A, C, E) and elastic spherical shell (B, D, F) (A, B)20° incidence; (C, D)40° incidence; (E, F)60° incidence. |
为了进一步了解不同发射角度时散射声场的变化特点,在图 7中亦绘出了入射角度分别为40°和60°时的刚性球体和弹性球壳的散射声场。40°入射时,刚性球体散射声场的最大幅度比弹性球壳的大、最大幅度对应的位置更接近目标(x=0m)处。入射角为60°时,刚性球体散射声场出现了两个起伏、而弹性球壳情况仍为一个,与弹性球壳相比刚性球体峰值附近的幅度明显要小。
综合比较上述结果可以发现:不同入射角时刚性球体散射声场幅度变化差别较大、峰值幅度变化较小,而弹性球壳的幅度变化差别较小、峰值幅度变化较大。
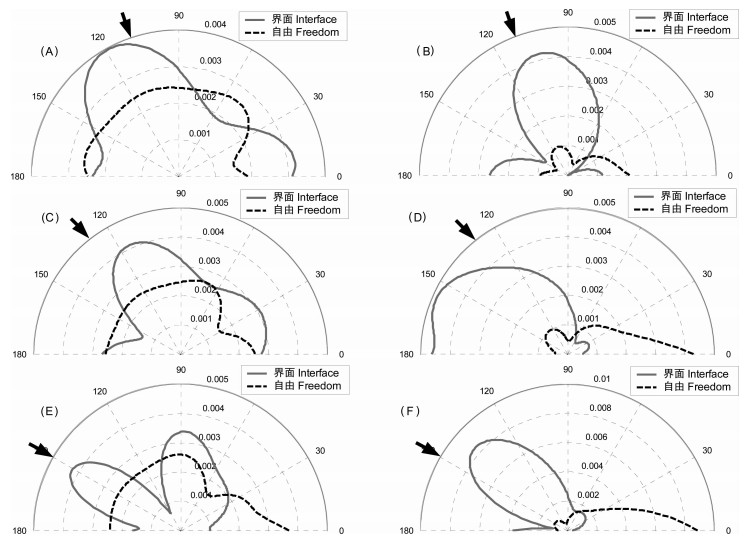
将目标的散射声场以散射图案的形式表示是方便的,图 8是对应图 7中不同入射角度和目标的散射图案(注:入射角度的方向在各图中已用箭头标示出,另未按声源距离归一)。为了研究界面的影响,图中还给出了自由流体空间中刚性球体和弹性球壳的散射声场(图中虚线),自由空间目标声散射图案形状相同、不同入射角度对应于不同的观察方向。由散射图案的对比除了可以获得与上述散射声场类似的结果外,还可以发现另外一些特点:界面上刚性球体和弹性球壳的反向(90°~180°)散射能量均大于反射方向(0°~90°)散射能量,而且弹性球壳的反向散射能量相对更大; 以入射角度为参考,刚性球体散射能量最大处所对应的角度偏离方向几乎与弹性球壳情况相反。
|
图 8 刚性球体(A,C,E)与弹性球壳(B,D,F)的散射图案(A,B)20°入射;(C,D)40°入射;(E,F)60°入射. Fig. 8 Scattering pattern of rigid sphere (A, C, E) and elastic spherical shell (B, D, F) (A, B)20° incidence; (C, D)40° incidence; (E, F)60° incidence. |
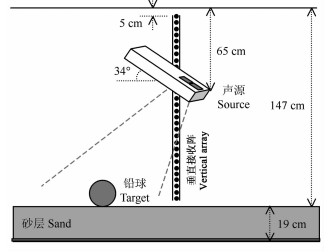
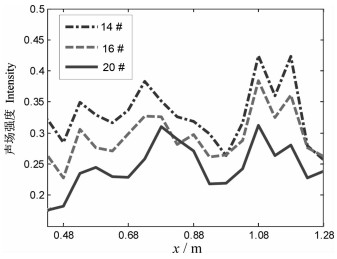
实验在两侧面消声的实验室波导中进行(图 9),其中水深约1.47m、底部铺设的砂层厚度约0.19m,直径约11cm的实心铅球置于底部某一位置。以长为20cm宽为10cm换能器作为声源、发射频带为20~40kHz的线性调频信号,发射波束具有指向性(纵向18°、横向28°)。以4cm间距32基元的垂直阵作为接收,将由上至下的32个阵元记为1#至32#。声源与垂直阵布设在同一移动平台上、倾斜34°向下扫描探测。在对目标进行探测前,首先对目标预放置区域进行扫描探测获得无目标时的混响信号。图 10是通过数据分析后得到的14#、16#和20#阵元记录的声场强度,其中横坐标是接收阵相对目标位置的水平距离。由于位于垂直阵上端的14#阵元具有相对入射的更小垂直角度,所以图中14#、16#和20#的声场强度依次减小,且该规律在0.85 m的水平距离内基本保持不变,在部分距离上强度起伏较大及突变是由承载砂层的钢板非均匀引起。
|
图 9 实验布设示意图 Fig. 9 Schematic of the experiment |
|
图 10 混响的声场强度 Fig. 10 Intensity of acoustic field in reverberation |
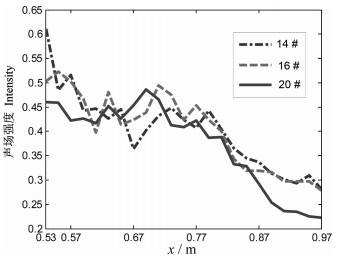
扫描探测铅球的分析结果如图 11所示。在远距离处三个阵元的声场强度与对应距离处混响的声场强度量级和变化基本一致,而在约0.85m以内三个阵元的声场强度均开始逐渐增加,这说明开始接收到逐渐增强的目标散射能量。值得注意的是:目标回波的强度并不是始终增加,而是有一定的起伏变化; 另外,约在0.67~0.70m段三个阵元的声场强度出现了反序(即14#、16#和20#的声场强度依次增加),而且在该反序和其两边正序的区段有不同阵元的声场强度多次交叉现象。在图 12中给出由本文模型计算的同样布设的30kHz单频点源的目标回波强度,与实验类似也有强度起伏变化。在图中可以看出:在1.3m处14#和16#开始交叉,随后两者约在1.15m处穿过20#形成反序,然后约在0.9m处再次穿过20#,并在0.78m处再次交叉后回到正序状态。这一变化过程与图 11实验结果中0.79~0.53m段的变化过程相似,其中变化的水平距离和强度差异可能主要是由实验中底部散射和模型中点源近似引起。
|
图 11 实验测量的目标回波强度 Fig. 11 Intensity of target's echo in experiment |

|
图 12 模型计算的目标回波强度 Fig. 12 Intensity of target's echo in calculation |
本文基于目标声散射的T矩阵方法并利用复像方法将平面海底界面上目标的声散射模型扩展到了点源入射情况,给出了物理机制更加清晰的散射声场计算公式,在此基础上可以进一步建立有限波束入射和界面上目标的三维声散射模型。T矩阵方法不能用于目标与界面有交叠的声散射问题,对于海底掩埋目标的声散射建模可以利用类似的处理方法,但要考虑声透射系数的多极展开以及目标散射透出界面的散射基函数等。这将是下一步的研究工作。
利用复像方法可以将由球面波展成柱面波叠加时的积分计算简化为多个复像的求和计算,由此利用Matlab中的矩阵或数组运算可以提高计算效率。本文根据Prony方法确定出了反射系数的估计系数(或复像的幅度和位置),通过与解析的反射系数和半空间格林函数的计算比较,证明了该方法的正确性。另外,与数值积分得到的向外辐射基函数比较算例说明了计算的准确性。
为了了解界面的影响以及不同目标的声散射特点,文中主要对不同入射方向的界面上刚性球体和弹性球壳的散射声场做了数值考察。单次散射近似的计算结果表明:对于文中所给参数情况,目标的反向(90°~180°)散射能量均大于反射方向(0°~90°)散射能量,而且弹性球壳的反向散射能量相对更大; 与自由空间目标声散射不同,不同角度、不同目标的声场散射图案差别较大,另外,两种目标的以入射角度为参考的能量最大对应角度的偏离变化趋势几乎相反。
在实验室波导中设计了利用垂直阵接收沉底铅球回波的扫描探测实验,以反映不同仰角的14#、16#和20#阵元为主分析了声场强度的次序变化及随水平距离的变化,并与模型的计算结果进行了比较。计算中得到的各阵元声场强度起伏、交叉及反序等规律与实验结果基本一致。
致谢作者曾就有关方法与中国科学院声学研究所的张碧星教授、瑞典理论物理研究所的A.Boström教授和美国海岸系统研究站的R.Lim教授进行过有益的讨论和交流, 在此深表谢意.
| [1] | Pinto M A, Bellettini A, Hollett R, et al. Real-and synthetic array signal proeessing of buried targets. IEEE.J.Ocean.Eng. , 2002, 27: 484-494. DOI:10.1109/JOE.2002.1040932 |
| [2] | Liu T C, Schmidt H. Concurrent navigation and sea-bottom targets detection using acoustic sensors on AUV. IEEE Proceedings of OCEANS'03 , 2003, 5: 2404-2409. |
| [3] | Tesei A, Maguer A, Fox W L J, et al. Measurements and modeling of acoustic scattering from partially and completely buried spherical shells. J.Acoust.Soc.Am. , 2002, 112: 1817-1830. DOI:10.1121/1.1509425 |
| [4] | Lucifredi I, Schmidt H. Suberitieal scattering from buried elastic shells. J.Acoust.Soc.Am. , 2006, 120: 3566-3583. DOI:10.1121/1.2357711 |
| [5] | Schmidt H. Virtual source approach to scattering from partially buried elastic targets. Proceedings High Frequency Acoustics Conference, San Diego, 1-5 March , 2004. |
| [6] | Moen I H, Dong H. Finite-difference modeling of scattering from shallow buried object in sea floor (A). J.Acoust.Soc.Am. , 2006, 120: 3380. |
| [7] | Waterman P C. New formulation of acoustic scattering. J.Acoust.Soc.Am. , 1969, 45(6): 1417-1429. DOI:10.1121/1.1911619 |
| [8] | Peterson B, Strom S. Matrix formulation of acoustic scattering from muhilayered scatterers. J.Acoust.Soc.Am. , 1975, 57(1): 2-13. DOI:10.1121/1.380397 |
| [9] | Kristensson G, StrOm S. Scattering from buried inhomogeneitiesa general three-dimensional formalism. J.Acoust.Soc.Am. , 1978, 64(3): 917-936. DOI:10.1121/1.382052 |
| [10] | Kristensson G, Strom S.The T matrix approach to scattering from buried inhomogeneities.In:Varadan V K, Varadan V V ed.Acoustic, Electromagnetic and Elastic Wave Scattering--Focus on the T-matrix Approach.New York:Pergamon, 1980.135-167 |
| [11] | Lira R, Lopes J L, Hackman R H, et al. Scattering by objects buried in underwater.sediments:theory and experiment.. J.Acoust.Soc.Am. , 1993, 93(4): 1762-1783. DOI:10.1121/1.406719 |
| [12] | Bishop G C, Smith J. Scattering from an elastic shell and a rough fluid-elastic interface:theory. J.Acoust.Soc.Am. , 1997, 101(2): 767-788. DOI:10.1121/1.417962 |
| [13] | Schmidt H, Lee J. Physics of 3-D scattering from rippled seabeds and buried targets in shallow water. J.Acoust.Soc.Am. , 1999, 105: 1605-1617. DOI:10.1121/1.426700 |
| [14] | Lim R, Williams K L. Thorsos E L Acoustic scattering by a three-dimensional elastic object near a rough surface. Acoust.Soc.Am. , 2000, 107: 1246-1262. DOI:10.1121/1.428414 |
| [15] | Simpson H J, Houston B H, Lin R. Laboratory measurements of sound scattering from a buried sphere above and below the critical angle (L). J.Acoust.Soc.Am. , 2003, 113: 39-42. DOI:10.1121/1.1523310 |
| [16] | "Scattering from objects near boundaries" in Acoustica'08 Paris, Acta Acustica united with Acustica, Vol.94 (Suppl.1), 2008.S975-S979 |
| [17] | Bishop G C, Smith J. Scattering from rigid and soft targets near a planar boundary:numerical results. J.Acoust.Soc.Am. , 1999, 105(1): 130-143. DOI:10.1121/1.424625 |
| [18] | Fawcett J A, Fox W L J, Maguer A. Modeling of scattering by objects on the seabed. J.Acoust.Soc.Am. , 1998, 104(6): 3296-3304. DOI:10.1121/1.423969 |
| [19] | Fawcett J A, Lira R. Evaluation of the integrals of target/ seabed scattering using the method of complex images. J.Acoust.Soc.Am. , 2003, 114(3): 1406-1415. DOI:10.1121/1.1600726 |
| [20] | Yang J J, Chow Y L, Fang D G.Discrete Complex Images of a Three-Dimensional Dipole Above and Within a Lossy Ground.Proc.Inst.Elect.Eng., Vol.138.Aug.1991.319-326 |
| [21] | Li Y L, White M J. Near-field computation for sound propagation above ground --Using complex image theory. J.Acoust.Soc.Am. , 1996, 99: 755-760. DOI:10.1121/1.414652 |
| [22] | Bostrom A. Scattering of stationary acoustic waves by an elastic obstacle immersed in a fluid. J.Acoust.Soc.Am. , 1980, 67(2): 390-398. DOI:10.1121/1.383925 |
| [23] | Brekhovskikh L M.Waves in Layered Media.New York:Academic, 1980, 2nd.sec.26.4, 32.2 |
| [24] | Morse P M, Feshbach H.Methods of Theoretical Physics.New York:McGraw-Hill, 1953.Chap.11 |
| [25] | Hackman R H, Sammelmann G S. Multiple scattering analysis for a target in an ocean waveguide. J.Acoust.Soc.Am. , 1988, 84: 1813-1825. DOI:10.1121/1.397148 |
 2010, Vol. 53
2010, Vol. 53