2. 清华大学数学科学系, 北京 100084;
3. 中国石油勘探开发研究院石油物探技术研究所, 北京 10008
2. Department of Mathematical Sciences, Tsinghua University, Beijing 100084, China;
3. Research Institute of Petroleum Exploration and Development, PetroChina, Beijing 100084, China
近20年来的油气资源勘探表明,在新发现的油气藏中致密性、隐蔽性油气藏占有非常重要的地位.随着我国常规油气产量高峰即将过去,非常规致密油气藏将是油气勘探开发的主要对象,非常规致密油气藏的基本特征是:孔隙度小(5%~12%)、渗透率低((0.1~1)×10-15m2).一般地,低孔渗储层的油气富集区多为缝隙发育区,其缝隙结构复杂,通常为非均匀各向异性的地质结构.同时,对于含流体缝隙介质,由于缝隙介质的自组织临界态特征和流体对固体的弱化作用,致使地球介质既有固体的弹性性质,又有流体的某些特征(如黏滞性等).由于低孔渗储层介质具有如此复杂的地质特征,因此应用常规的勘探理论模型和方法难以进行有效的储层预测.
岩石物理模型的研究有助于了解复杂储层介质中波传播的规律,进而指导实际的油气勘探,譬如经典的Biot理论[1, 2]和Gassmann方程[3]等.研究发现:在含流体的孔隙介质中,Biot流动和喷射流动是孔隙介质中两种重要的流动形式.当波在孔隙介质中传播时,Biot流动和喷射流动作为一个耦合过程共同对波的传播产生影响.1993年,Dvorkin和Nur给出了基于弹性统计各向同性孔隙介质的BISQ模型[4],该模型将孔隙介质中流体流动的细观机制与宏观变量有机统一起来,很好地解释了实验中观测到的高频散和强衰减现象,其有效性已经为众多学者的研究工作所验证[5~11].基于BISQ模型的波场特性分析和储层参数反演等研究工作拓展了该模型的应用范围[12, 13].
本文在各向同性弹性BISQ模型的基础上,综合考虑孔隙流体的两种流动力学机制、岩石骨架的各向异性、黏弹性力学机制以及泥质含量等,定义了各向异性黏弹性参数修正因子,并将其引入到黏弹性模型中,从而给出了描述低孔渗含泥质孔隙各向异性介质中波传播规律的黏弹性BISQ模型,进而获得了基于“频率-波数”域的相速度和衰减解析解,重点研究了渗透率、方位角、黏弹性参数等因素对波传播响应的影响规律.
2 含泥质孔隙各向异性黏弹性BISQ模型 2.1 孔隙各向异性介质固-流耦合动力学方程对于孔隙各向异性介质,应用一个特征六面体微元分析固-流双相介质系统的应力-应变关系.根据Biot(1956)理论[1],选取固相和流相的平均位移ui和Ui为基本未知量,其中下标i分别取1、2、3代表笛卡儿坐标系的三个正交方向.给出动能函数T和耗散函数D,由拉格朗日方程不难给出作用于微元体固相和液相部分的广义力;同时,由忽略了外力作用的平衡方程可以得到微元体上的广义力和总应力σij和流体压力P的关系.这样,就可以导出不考虑外力情况下基于固-流耦合各向异性效应的动力学方程[6]:

|
(1) |
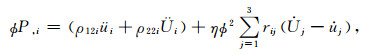
|
(2) |
其中:ρ1=(1-Φ)ρs,ρ2=Φρf,Φ是孔隙度,ρf和ρs分别为流相和固相的密度,ρ22i=ρ2-ρ12i,ρ12i=-ρai,ρai(i=1,2,3)为xi方向的附加惯性质量密度,η为流体黏度,流体阻抗系数(rij)=(kij)-1(i,j=1,2,3),kij为渗透率系数.式中,物理量上标的小圆点表示对时间t的导数,即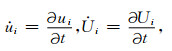
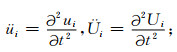
从孔隙流体质量守恒方程出发,可以给出宏观Biot流机制作用下的孔隙流体压力变化率与固相和流相位移间的函数关系式.1993年,Dvorkin和Nur[4]给出了1D各向同性介质中宏观Biot流机制和微观喷射流机制共同作用下的孔隙流体压力表达式.进一步地,Yang和Zhang[7]给出了三维各向异性孔隙BISQ模型中的流体压力为
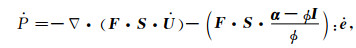
|
(3) |
其中:Biot流系数张量F、喷射流系数张量S以及有效弹性系数张量α的定义见文献[7],固相骨架应变张量e的分量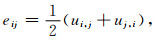
考虑实际地球岩石中通常赋含泥质或封闭的孔隙流体等软杂质,对骨架起到弱化的作用,通常可以用黏弹性本构关系来描述这样的应力-应变关系.在最近的工作中,我们给出了孔隙各向同性黏弹性BISQ模型来描述波传播过程中固体骨架所表现出来的这种黏滞性[8, 9].本文将其推广到孔隙各向异性固-流双相介质情况,则总应力与固相位移和流体压力之间的关系为
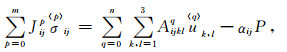
|
(4) |
其中,符号算子〈P〉表示对时间t的P阶导数,即〈P〉=∂P/∂tP.Jij0=1,Aijkl0为弹性系数,JijP和Aijklq为黏弹性系数(P=1,2,…,m;q=1,2,…,n).
因此,方程(1)~(4)就组成了含饱和流体孔隙各向异性介质中黏弹性BISQ模型的波动力学控制方程组.这是一组封闭的时间-空间域方程组,通常可以用差分法或伪谱法等数值方法求解.本文将其变换到频率-波数域,通过假设平面谐波解推导相速度和衰减系数的解析式.首先对方程(1)~(4)进行傅里叶变换,得到频率-空间域内的方程组:
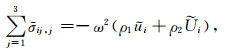
|
(5) |
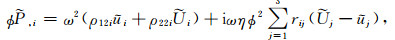
|
(6) |
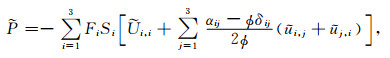
|
(7) |

|
(8) |
其中,ω为波的角频率,黏弹性参数βJ和βA分别为
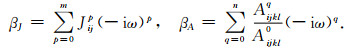
|
对式(8)求散度代入式(5)中消去应力项,整理式(6)得到流体位移后代入式(5)和式(7)中消去流体位移项,则得到由固相位移ui和孔隙流体压力P为基本未知量的频率-空间域黏弹性BISQ模型波动方程:
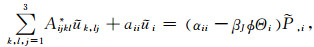
|
(9) |
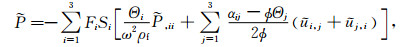
|
(10) |
其中:
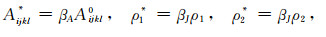
|
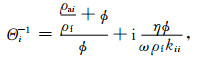
|

|
对于一般孔隙各向异性介质的黏弹性BISQ模型很难求出解析解.本文研究孔隙横向各向同性介质(即PTL介质)中波的频散和衰减规律,该理论模型可描述水平层状储层介质,此时黏弹性BISQ模型波动力学控制方程式(9)和(10)可简化为
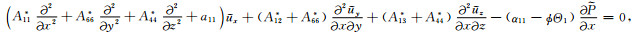
|
(11) |
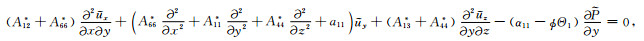
|
(12) |
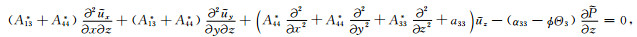
|
(13) |
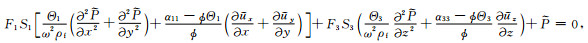
|
(14) |
其中,Aij*=βAAij0(i,j=1,2,3),Aij0为横向各向同性孔隙介质固体骨架的弹性模量;横向各向同性介质的孔隙弹性系数α11=α22=1-(A11+A12+ A13)/3Ks,α33=1-(2A13+A33)/3Ks.
在我们最近的研究中,根据对不同渗透率含泥质砂岩岩样的超声波实验数据分析,我们引入了黏弹性参数修正因子用来描述孔隙各向同性介质的渗透率和泥质含量对波传播过程中能量衰减的影响[8],并通过与实验数据的比较证实了引入这一修正参数的有效性和正确性.本文将这一黏弹性参数修正因子推广到孔隙各向异性介质的黏弹性BISQ模型中,并定义各向异性黏弹性参数修正因子如下:
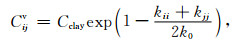
|
(15) |
其中:Cclay为泥质含量,kii为xi方向的渗透率(i=1,2,3),另k44=k11,k55=k22,k66=k33.对目前我们所研究的低孔渗介质情况,选取基础渗透率k0=0.5×10-15m2,其值可通过反演实测的波速和衰减值确定[8].这种参数修正因子的物理意义在于:在修正后的黏弹性BISQ模型中,低渗透率范围内骨架的黏弹性力学机制和喷射流动机制对波衰减的影响较大;随着孔隙连通性的增强,孔隙流体的两种流动机制在波传播过程中的作用逐渐增强;在较高的渗透率范围内,Biot流动机制和喷射流动机制对波传播过程中的能量损失起到的作用要远大于骨架黏弹性力学机制对波传播的影响.这一点在后面的数值模拟中将做进一步的解释和说明.
通过引入修正因子(15),方程(11)~(14)中的黏弹性参数可修正如下:
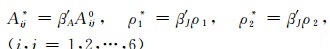
|
(16) |
其中,
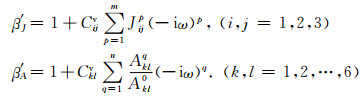
|
(17) |
对于Kelvin-Voigt型黏弹性介质有m=n=1,则式(17)可化简为
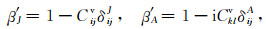
|
(18) |
其中,δijJ=ωJij1,δklA=ωAkl1/Akl0.
2.4 波的相速度和衰减欲求解频率-空间域内的各向异性黏弹性BISQ方程,需要将其控制方程变换到频率-波数域[10, 11].为此,首先假设空间域内固相位移和孔隙流体压力具有如下形式的平面谐波解:
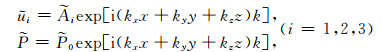
|
(19) |
再将式(19)代入式(11)~(14)中,整理得到:
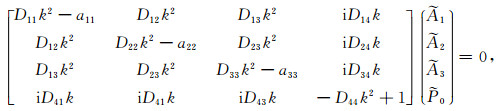
|
(20) |
方程(19)和(20)中的k为波数,ki为波传播方向与坐标轴xi(x1、x2和x3分别对应于x、y和z)夹角的方向余弦;Dij(i,j=1,2,3)分别如下:
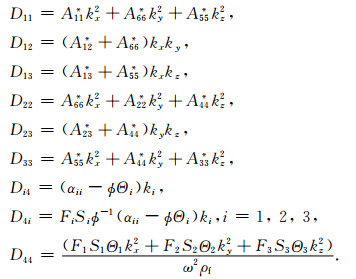
|
若使
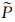
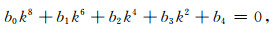
|
(21) |
式中的系数项bi(i=0,1,2,3,4)见文献[7].但需要注意的是,文献[7]中的bi为正交各向异性介质BISQ模型的系数,而对于本文模型,只需将文献[7]中的包含于系数bi中的常数A55,A22,A23,α22分别用A44,A11,A13,α11代替即可.
一般情况下,波数方程式(21)有四个不同的根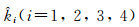
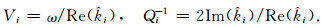
|
(22) |
通常,很难通过方程式(21)的解析解分析波传播的频散和衰减规律,但可以就某些特殊传播方向的平面波性质进行讨论.下面将讨论xoz平面内传播的平面波性质,此时可令kx=sinθ,ky=0,kz=cosθ,其中θ为入射平面波与z轴的夹角.由方程(21)得:
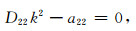
|
(23) |
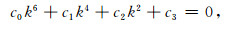
|
(24) |
其中:
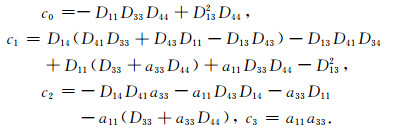
|
由方程(23)可得拟SH波的波数解,由方程(24)得拟快P波、拟慢P波和拟SV波的波数解,分别代入上述相速度和衰减逆品质因子的计算公式(22),即可得到四种波在孔隙各向异性介质中传播的相速度和衰减逆品质因子.
3 数值计算首先,考察在xoz平面内沿x轴传播时渗透率和频率对孔隙PTL介质中波响应的影响.为此,选取模型参数为:孔隙度Φ=0.1,固相密度ρs=2650 kg/m3,固相体积模量Ks=38 GPa,干骨架弹性模量A11=30.15 GPa,A13=5.695 GPa,A33=24.79 GPa,A44=10.05 GPa,A66=13 GPa,流体密度ρf=1000 kg/m3,固流耦合密度ρax=ρaz=420 kg/m3,特征喷射流动长度R1=R3=2 mm,x轴方向的渗透率分别为k11=0.1×10-15,0.5×10-15,1×10-15m2,z轴方向垂直渗透率k33=0.1×10-15m2,参考渗透率为k0=0.5×10-15m2,孔隙流体黏度为η=0.001 Pa·s,泥质含量Cclay=15%,黏弹性参数δijJ=0.1(i,j=1,2,3),δ11A=δ33A=0.3,δ44A=δ66A=δ13A=0.1.图 1显示了不同渗透率情况下频率对快P波、慢P波相速度和衰减逆品质因子的影响.
|
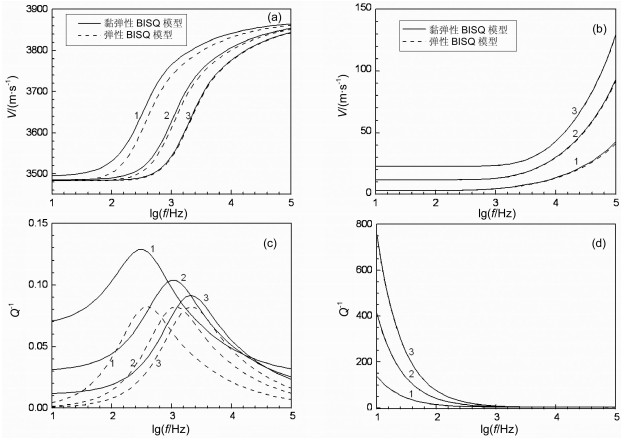
图 1 渗透率对波频散(a,b)和衰减(c,d)的影响 (a,c)快P波;(b,d)慢P波.线1、2、3分别为x方向渗透率k11=0.1×10-15,0.5×10-15,1×10-15m2. Fig. 1 The effect of permeability on wave dispersion (a, b) and attenuation (c, d) (a, c) Fast P-wave; (b, d) Slow P-wave.Line 1, 2, and 3 correspond to different permeabilities of 0.1×10-15m2, 0.5×10-15m2, and 1×10-15m2 in thex-direction, respectively. |
从图 1a可以发现,快P波的相速度从低频到高频存在一个过渡带,并随着渗透率的增加向高频方向移动;图 1c表明,对应于衰减峰值的频率随渗透率的增加而增大.其物理意义是:在低频情况下渗透率越小孔隙流体的喷射流动越不容易变得松弛.图 1d显示在低频域内慢P波迅速衰减,这就是我们在地震波勘探频率范围很难观测到慢P波的原因.这些规律的变化趋势对于弹性BISQ模型和黏弹性BISQ模型是基本一致的.另外,从图 1a中可以看出黏弹性BISQ模型和弹性BISQ模型中快P波的频散规律基本相同,前者预测的理论波速要大于后者. 图 1c的实线表明,随着渗透率的降低黏弹性BISQ模型的衰减逆品质因子不断增大,其物理意义是:随着孔隙介质渗透率的降低,含泥质岩石骨架的孔隙连通性变差,越来越多的孔隙流体在波传播过程中成为封闭或半封闭的孔隙流体,好似一个个嵌于固体骨架内的“粘壶”,使得波在传播过程中呈现一定的黏滞性,这种固体骨架的黏弹性力学机制对低孔渗含泥质岩石中波的强衰减起主要作用.
下面研究波传播方向、渗透率、泥质含量等参数对波频散和衰减的影响.考察在声测井频率范围f=10 kHz和地震波频率范围f=50 Hz情况下xoz平面内波的传播方向对不同泥质含量的孔隙PTL介质中波响应的影响.模型参数选取为:x轴方向的渗透率k11=0.1×10-15m2、z轴方向垂直渗透率k33=0.5×10-15m2,取x方向的渗透率为参考渗透率,其余参数同上例.图 2和图 3显示了两种典型频率下不同泥质含量的岩石中波传播方向对拟快P波、拟慢P波、拟SV波和拟SH波的相速度和衰减逆品质因子的影响,其中:实线和虚线分别为黏弹性、弹性BISQ模型,线1、2、3分别代表泥质含量5%、10%、15%.
|
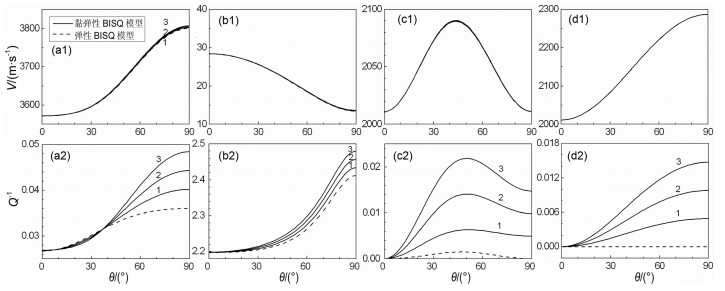
图 2 测井频域内(f=10 kHz)波传播方向对波相速度和衰减的影响 (a1,a2)拟快P波;(b1,b2)拟慢P波;(c1,c2)拟SV波;(d1,d2)拟SH波. Fig. 2 The effect of angle of propagation on phase velocity and attenuation at the well-logfrequency (f=10 kHz) (a1, a2) Fast quasi-P-wave; (b1, b2) Slow quasi-P-wave; (c1, c2) Quasi-SV-wave; (d1, d2) Quasi-SH-wave |
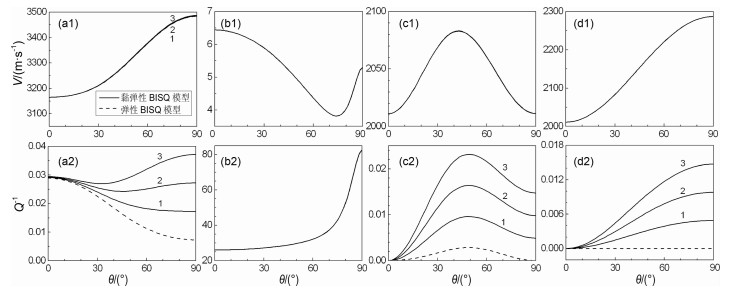
从图 2和图 3中可以看出,对于弹性BISQ模型而言,拟快P波的相速度随着入射波角度的增加而增大,当波沿着渗透率最小的方向(90°即x轴)传播时其相速度最大.比较图 2a2和图 3a2可看出,在测井频域,拟快P波的衰减逆品质因子随入射波角度的增加而增大;在地震频域,其变化规律正好相反.其物理意义是:在高频情况下,渗透率越小,孔隙流体越容易松弛;在低频情况下,渗透率越大,孔隙流体越容易松弛.对于黏弹性BISQ模型而言,拟快P波的衰减逆品质因子的变化趋势与弹性BISQ模型基本一致,只是由于骨架黏弹性力学机制的引入,当波沿渗透率最小方向传播时,其衰减峰值要大于弹性BISQ模型所预测的衰减值,而且随着泥质含量的增加其衰减峰值也随之增大.尤其是在地震频率范围内,当低孔渗储层介质的泥质含量较高时,拟快P波的衰减峰值出现在渗透率最小的方向上,这个结论与弹性BISQ模型结论相反.其物理意义是:在低频情况下,骨架的黏弹性力学机制对波传播的影响已经超过了两种孔隙流体流动机制(Biot流机制和喷射流机制)对波的影响而占据主导地位.从图 2和3可以看出,在低孔渗介质中慢拟P波的速度非常小,特别是在地震频率范围,其速度更小,几乎可以看成没有慢P波产生.其物理含意是,在含有流体的低孔隙度和低渗透率储层介质中,由于流体的不易流动,致使流体和固体粒子相对运动更为困难、更难观测到慢速P波.另外,图 2和图 3表明,黏弹性BISQ模型的拟SV波和拟SH波的衰减逆品质因子表现出显著的各向异性.由于岩石物理模型中的各向异性渗透率与复杂储层介质中裂隙和裂缝的定向排列密切相关,因而这些结论对于低孔渗储层介质的油气勘探具有重要的参考价值.
|
图 3 地震波频域内(f=50 Hz)波传播方向对波相速度和衰减的影响 (a1,a2)拟快P波;(b1,b2)拟慢P波;(c1,c2)拟SV波;(d1,d2)拟SH波.实线和虚线分别为黏弹性、弹性BISQ模型,线1、2、3分别代表泥质含量5%,10%,15%. Fig. 3 The effect of angle of propagation on phase velocity and attenuation at the seismic frequency (f=50 Hz) (a1, a2) Fast quasi-P-wave; (b1, b2) Slow quasi-P-wave; (c1, c2) Quasi-SV-wave; (d1, d2) Quasi-SH-wave. The solid and dashed lines correspond to viscoelastic and elastic BISQ model, respectively. Lines 1, 2, and 3 denote the clay contents of 5%, 10%, and 15%, respectively. |
在最后的数值例子中,我们基于本文的改进黏弹性BISQ模型,研究孔隙PTL介质中频率和波传播方向的影响,考察二维(x-z)情况下波传播方向及频率对波相速度和衰减的影响.模型参数选取为:干骨架弹性模量A11=35 GPa,A13=10 GPa,A33=30 GPa,A44=15 GPa,A66=13 GPa,各方向的渗透率为k11=0.2×10-15m2、k33=0.5×10-15m2,泥质含量30%,其余参数同上例.波传播方向与z轴的夹角范围:0°~90°,波频率范围:101~105 Hz.图 4为波传播方向及频率对拟快P波和拟SV衰减逆品质因子的影响,其中图 4a、4c为弹性BISQ模型;图 4b、4d为黏弹性BISQ模型.
|
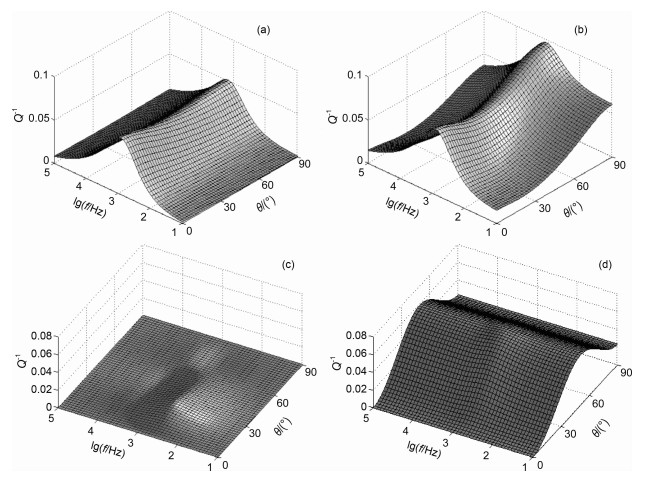
图 4 波传播方向与频率对拟快P波(a,b)和拟SV波衰减的影响(c,d) (a,c)为弹性BISQ模型;(b,d)为黏弹性BISQ模型. Fig. 4 The effects of angle of wave propagation and frequency on the fast quasi-P-wave attenuation (a, b) and the quasi-SV-wave attenuation (c, d) (a, c) Elastic BISQ model; (b, d) Viscoelastic BISQ model. |
从图 4a和4b可以看出,两种BISQ模型预测的拟快P波的衰减逆品质因子随频率的变化规律基本趋于一致,即衰减峰值都出现在1000 Hz左右.然而,在低频率范围内(10~100 Hz),黏弹性BISQ模型预测的衰减逆品质因子随入射波角度的增加而增大,当频率一定时,其衰减峰值出现在渗透率最小的方向上,且远远大于弹性BISQ模型的衰减理论值.其物理意义是在低频情况下,低孔渗储层介质中的孔隙流体不容易松弛,固体骨架的黏弹性力学机制对波传播的影响起主要作用,并且这种黏滞性呈现较强的各向异性.对拟SV波,从地震波频率到更高频率范围内,黏弹性BISQ模型预测的衰减值(图 4d)比弹性BISQ模型预测的衰减值(图 4c)都大,且表现出强烈的各向异性.拟快P波和拟SV波衰减的这些各向异性特征可以用来进行裂缝方位预测和各向异性渗透率的拾取等研究.
4 结论本文综合考虑了复杂储层介质波传播过程中两种重要的孔隙流体流动机制(Biot流机制和喷射流机制)、固体骨架的各向异性以及黏弹性力学机制相互耦合作用情况下对不同波传播的影响,给出了可以描述含泥质低孔渗各向异性介质中波传播规律的黏弹性BISQ模型,进一步给出了某些特殊情况下四种波的相速度和衰减逆品质因子;通过数值算例研究了各向异性渗透率、波入射角度、频率、泥质含量等因素对波传播的响应特征.研究结果表明,当波沿着渗透率最小的方向传播时,黏弹性BISQ模型预测的拟快P波衰减逆品质因子最大,随着泥质含量的增加其衰减峰值随之增大;尤其是在低频情况下(地震勘探频率),低孔渗储层介质的骨架黏弹性力学机制对波传播过程中的振幅衰减占主导地位;黏弹性BISQ模型的拟SV波和拟SH波的衰减呈显著的各向异性.这些结果对于深入研究复杂储层介质的波传播规律、储层特征以及提高非常规致密油气田的勘探精度具有重要的理论价值和实际意义.
| [1] | Biot M A. Theory of propagation of elastic waves in a fluidsaturated porous solid Ⅰ.Low-frequency range. J Acoust Soc Amer , 1956, 28(2): 168-178. DOI:10.1121/1.1908239 |
| [2] | Blot M A. Theory of propagation of elastic waves in a fluidsaturated porous solid Ⅱ.Higher frequency range. J Acoust Soc Amer , 1956, 28(2): 179-191. DOI:10.1121/1.1908241 |
| [3] | Gassmarm F. Uber die elastizat poroser medien. Vierteljahrsschrift der Natruforschenden Gesellschaft in Zurich , 1951, 96: 1-23. |
| [4] | Dvorkin J, Nur A. Dynamic poroelasticity: a unified model with the squirt and the Blot mechanisms. Geophysics , 1993, 58(4): 524-533. DOI:10.1190/1.1443435 |
| [5] | Dvorkin J, Nolen-Hoeksema R, Nur A. The squirt-flow mechanism: macroscopic description. Geophysics , 1994, 59(3): 428-438. DOI:10.1190/1.1443605 |
| [6] | Yang D H, Zhang Z J. Effects of the Blot and the squirt-flow coupling interaction on anisotropic elastic waves. Chinese Science Bulletin , 2000, 45(23): 2130-2138. DOI:10.1007/BF02886316 |
| [7] | Yang D H, Zhang Z J. Poroelastic wave equation including the Biot/squirt mechanism and the solid/fluid coupling anisotropy. Wave Motion , 2002, 35(3): 223-245. DOI:10.1016/S0165-2125(01)00106-8 |
| [8] | Nie J X, Yang D H. Viscoelastic BISQ model for lowpermeability sandstone with clay. Chinese Physics Letters , 2008, 25(8): 3079-3082. DOI:10.1088/0256-307X/25/8/092 |
| [9] | Nie J X, Yang D H, Yang H Z. A generalized viscoelastic Blot/squirt model for clay-hearing sandstones in a wide range of permeabilities. Applied Geophysics , 2008, 5(4): 249-260. DOI:10.1007/s11770-008-0038-y |
| [10] | Parra J O. The transversely isotropic poro-elastic wave equation including the Blot and the squirt mechanisms: theory and application. Geophysics , 1997, 62: 309-318. DOI:10.1190/1.1444132 |
| [11] | Zhang Z J, Teng J W, He Z H. Azimuthal anisotropy of seismic velocity, attenuation and Q value in viscous EDA media. Science in China (Series E) , 2000, 43(1): 17-22. |
| [12] | 聂建新, 杨顶辉, 杨慧珠. 基于非饱和多孔隙介质BISQ模型的储层参数反演. 地球物理学报 , 2004, 47(6): 1101–1105. Nie J X, Yang D H, Yang H Z. The inversion of reservoir parameters based on the BISQ model in partially saturated porous medium. Chinese J.Geophys (in Chinese) , 2004, 47(6): 1101-1105. |
| [13] | 杨宽德, 杨顶辉, 王书强. 基于Blot-squirt方程的波场模拟. 地球物理学报 , 2002, 45(6): 853–861. Yang K D, Yang D H, Wang S Q. Wave-field simulation based on the Blot-squirt equation. Chinese J.Geophys (in Chinese) , 2002, 45(6): 853-861. |
 2010, Vol. 53
2010, Vol. 53

