Born近似,即一阶Born逼近是1933年由Born在研究量子散射时提出的[1].半个世纪以来,Born近似理论广泛应用于地球物理学研究,例如非均匀介质中的波传播模拟[2~4]、非线性地震反问题的线性化处理[5~9]和小尺度非均匀介质波散射问题的解析描述[10~13].地震波传播模拟的一阶Born逼近解,由于能量不守恒,需要严格的适用条件[14],即一阶Born逼近解在理论上只适用于弱横向非均匀介质(速度横向扰动小于10%).该假定及其对波现象的影响多年来得到广泛研究,并且已经取得了一些定量、半定量的结果.然而,在实际应用中,我们注意到Born近似取得了良好的应用效果,并不总是严格遵守小扰动假设[15].Born近似在地震散射分析中的应用综述可参阅Sato和Fehler著作[16].地震波在地壳中传播的数值模拟结果表明一阶Born逼近可以在一定传播距离内有效模拟地震波的小尺度分量[17],特别是模拟地震波形的相对变化具有较高的精度.
Ray-Kirchhoff传播算子是一种结构简洁、运用灵活、运算高效的横向变速单程波传播逼近算子[18],能够较为精确地描述波在非均匀介质中传播的运动学特征.由于其理论上的先天不足,Ray-Kirchhoff传播算子对复杂介质的成像效果极大地依赖于地震走时多路径射线追踪计算方法的精度[19~25].几乎所有单程波传播算子都是通过各种逼近方法导出,但高频近似对Ray-Kirchhoff单程波传播算子的影响是致命的[26],在实际复杂介质中,有限频波动的传播路径非常的复杂[27],入射角的微小变化会导致射线追踪结果的很大变化,阴影区和焦散区的存在引起大小不一的空白区和多值区,由于速度的剧烈变化,几乎无法得到正确射线路径. Born近似在单程波传播问题中的应用发展非常迅速,利用Born近似来化解Lippmann-Schwinger波动积分方程,可得到一类解单程波传播问题的Fourier方法.这类基于波动方程的Fourier单程波传播算子具有许多很好的特性,例如,算法结构简单、高效的运算(只用FFT作波场延拓)、自然满足Snell定律、无条件数值稳定、无网格频散和三维算子分裂误差、允许比有限差分算法更大的延拓步长等.由于速度变量是空间坐标的函数和Fourier变换的全局特性,Fourier单程波传播算子的主要研究内容是解决横向速度变化问题.对于弱速度对比介质或小角度传播,我们可以采用经典的分裂步Fourier单程波传播算子(SSF)[28, 29],或者相位屏[30]传播算子.近年来,Fourier单程波传播算子方法得到了进一步的发展和应用,主要是解决强速度对比介质和大角度传播问题.例如,广义屏算子[31~34]和分离变量屏算子[35~37].这些Fourier单程波传播算子只用FFT作波场延拓,保留了简单高效的相位屏算法结构,同时兼容更大的速度横向变化和传播角度.特别是分离变量屏算子,其波场延拓实际上是在f-k域对两个相位屏算子进行线性插值,每延拓一层只需3次FFT(比相位屏算法多一次),但适用于强速度横向变化.关于Fourier单程波传播算子的另一个主要进展是Fourier有限差分单程波传播算子(FFD)的研究,Collins[38],Ristow和Rühl[39]等利用Padé展开式逼近平方根方程,导出分裂步Padé单程波传播算子,在分裂步Fourier单程波传播算子中增加一有限差分补偿项,以适应强速度对比介质.
相位屏法可扩展为复屏法[40~42]来解决单程弹性波传播问题.Wu[30]总结了相位屏法的一些优点并讨论了不同波型的前向和后向散射的多种近似.我们注意到虽然相位屏法严格来说只适用于弱横向变化介质,但在实际应用中,它能模拟波在强非均匀介质中传播的某些特征.相位屏法的推导过程中有几个关键的近似,如Born近似、小角度近似、指数近似和扰动速度函数的简化,这些近似的同时,实际上将相位屏法的适用范围从Born近似的弱速度对比下的大角度传播拓展至强速度对比下的小角度传播.Fu[43]提出用Born频散方程来准确描述单程波传播中各阶Born近似的精度.实际上,可以通过修正Born频散方程,使相应的Fourier单程波传播算子兼容中等速度对比下的宽角度波传播.此修正的Born频散方程就是非均匀介质中一阶Born-Kirchhoff传播算子的频散关系[43, 44].
本文研究Born序列逼近在单程波传播中的应用.Born序列(或称Neumann级数)最初用于研究数值迭代求解古典积分方程,具有明确定义的收敛条件.这些成熟的理论和方法后来广泛用于研究波在随机介质中的传播和散射.Schuster[45, 46]将Born序列引入边界积分方程中研究多体散射问题,对波散射的Born序列逼近作了深刻的描述,最终的积分算子表明Born序列的每一阶逼近都有明确的物理解释,即描述了相邻散射体之间的相互作用次数,Born序列解的截断意味着散射体之间相互散射次数减少.对于边界散射波的研究,Born序列可应用于起伏地表的散射问题[47],结果表明一阶Born近似解考虑了观察点到边界点之间的一次散射,而二阶Born近似解描述了两个边界点之间的一次散射.对于非均匀介质的体散射问题,Fu等[48]通过广义Lippmann-Schwinger积分方程的Born序列逼近来研究SH波垂直入射到非均匀冲积河谷的无量纲频率响应问题,对非均匀介质体散射的Born序列逼近进行了详细的研究.在这个边界积分-体积分方程中,Born序列逼近只用于河谷内非均匀介质点,而对于河谷边界的散射波用全波形的隐式解.研究结果表明:体散射波的一阶Born近似只考虑了观察点到河谷内点之间的一次散射,忽略了边界点和内部点之间的多次散射,也忽略了任何内部点之间的散射;二阶Born近似不仅考虑了观察点到内部点间的一次散射,同时也考虑了边界点和内部点之间和两个内部点之间的一次散射.
对于单程波逼近,Born序列解能很好地模拟所有前向的散射波,忽略回传的散射波.对单程波传播算子品质进行评估需要考虑如下因素:理论逼近的合理性、数值实施的稳定性、算法结构的简单性、适应的介质非均质程度和地层倾角大小、计算效率等.一般地说,Fourier单程波传播算子不能有效地解决强速度对比问题.许多在波数域设计,理论上适用于强速度对比下宽角传播的Fourier单程波传播算子,由于在高波数奇异而未能进行稳定的数值实施.然而,这些波数域Fourier单程波传播算子的空间域版本是非奇异的,无条件数值稳定.本文通过Lippmann-Schwinger波动积分方程的Born序列逼近,导出各阶Born-Kirchhoff传播算子.Born-Kirchhoff传播算子的公式推导和物理解释在波数域进行,其精度分析和Born序列逼近的特征可通过Born序列频散方程进行详细研究.然而,Born序列频散方程不能解决数值稳定性问题.由于Born-Kirchhoff传播算子在空间域无条件稳定,可通过Kirchhoff求和进行数值实施,其各阶公式具有不同的精度,适应不同的介质非均质程度,需要不同的计算资源,可满足不同程度非均匀介质中的波传播模拟、地震成像和速度估计.
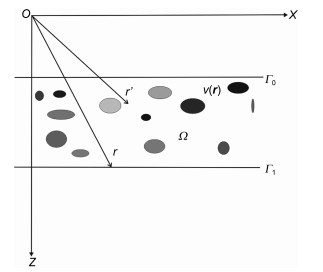
2 一阶Born-Kirchhoff传播算子我们考察任意非均匀薄板中的稳态标量波传播.如图 1所示,薄板围绕成区域Ω,包含顶面Γ0,底面Γ1和两端人工边界Γ∞,形成了一个闭合的边界Γ=Γ0+Γ1+Γ∞.薄板速度分布为v(r),其背景速度是v0.假设有一位于Γ0的已知波场沿Z轴从Γ0传播到Γ1.波与介质的相互作用包含Γ0和Γ1处的边界散射和薄层内非均匀性引起的体散射.位于r处的总波场u(r)满足如下的Lippmann-Schwinger积分方程:
|
图 1 一个非均匀薄板的示意图 Fig. 1 The geometry of a heterogeneous slab |
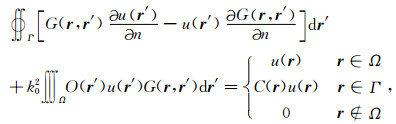
|
(1) |
其中∂/∂n表示边界Γ外法向导数,k0=v0/ω为背景波数,O(r)=n2(r)-1为相对慢度扰动,n(r)=v0/v(r)为声波折射率,G(r,r′)是背景介质中的自由空间格林函数,系数C(r)一般由r处局部几何形状决定,对于平面C(r)=0.5.方程(1)是第二类Fredholm积分方程,描述了非均匀薄板中的双程波传播.Fu[49, 50]讨论了该积分方程内、外Helmholtz边值问题的解,并应用该方程数值模拟了波在岩石圈中的传播.
将人工边界Γ∞沿X轴方向延伸至无穷远处,根据Sommerfeld辐射边界条件,沿Γ∞边界上的积分将消去.当r,r ′∈Γ1时,∂G(r,r′)/∂n=0,则方程(1)可改写为
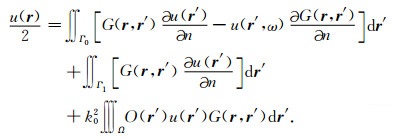
|
(2) |
双程波传播方程(2)有两个未知变量:波场u(r)和它的法向导数∂u(r)/∂n.与简化传统的Kirchhoff积分方程类似,可将该方程进一步简化为单程波传播形式.传统的Kirchhoff积分方程简化过程如下:(1)选取Γ0与Γ1为Dirichlet边界条件,一种“声软”边界条件,使G(r,r ′)=0,这样可以消去含∂u(r)/∂n的项;(2)忽略背景层Γ0与Γ1之间的层间多次反射,即没有能量从Γ1反射回到Γ0.这样可将Kirchhoff积分方程简化为瑞利型积分方程,用于单程波传播的计算.Berkhout和Wapenaar[51]提出一种单程波格林函数来消去Kirchhoff积分方程中的∂u(r)/∂n项.本文采用一种比“声软”边界条件更合理的方法来简化方程(2).对Γ0和Γ1应用如下的Sommerfeld无反射边界条件:
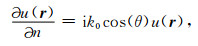
|
(3) |
式中θ为边界法线方向和传播路径r-r′之间的夹角.方程(3)实际上是一种吸收边界条件,使地震波从Γ0到Γ1层无反射传播.
考虑三维情况,取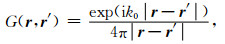
式中背景场
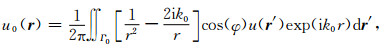
|
(5) |
式中r=|r-r
′|,cos(φ)=cos(180°-θ).在远场逼近条件下,即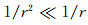
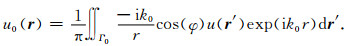
|
(6) |
通过傅氏变换到时间域,方程变为
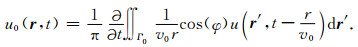
|
(7) |
由于远场逼近的波前平面化特点,即∂/∂t=(v0/cosφ)∂/∂x,方程(7)可改写为

|
(8) |
此积分表示沿绕射双曲面的振幅求和.
在二维情况下,取G(r,r
′)=iH0(1)(k0r)/4,式中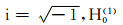
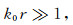

|
(9) |
将方程(3)代入方程(2)得到二维情况下的背景波场值
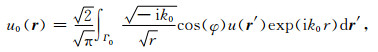
|
(10) |
及其时间域版本:
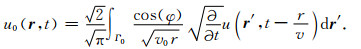
|
(11) |
方程(8)和(11)描述薄板中背景波场的传播,精度满足最大传播角达90°,在地震模拟[52, 53]和地震成像[54, 55]中得到了广泛的应用.Safar[56]分析了这些公式的地震成像横向分辨率,Yilmaz[57]进一步改善了Kirchhoff地震成像算子的实际应用效果.由于实际地震数据的有限带宽,Kirchhoff地震成像局限于有限孔径,孔径的选择对成像结果具有重要的影响[58, 59],通过菲涅耳带可以选取最佳孔径.
从方程(6)和(10)可知,Kirchhoff求和过程中有几个至关重要的因素影响地震成像的相位和振幅.球面扩散因子(三维情况下是1/r,二维情况下是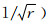
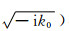
由于双程格林函数使得方程(4)中的体积分项可以描述薄板内初次和多次等双程波散射.这种场依赖的散射源使方程(4)变为非线性方程,即增加散射介质不是线性地增加散射场,并改变了整个场依赖散射源的分布.由于方程中未知量u(r)以隐式出现,地震模拟和成像需要解方程组.根据Born近似,将被积式中未知场u(r)替换成入射场u0(r),方程变为单程波传播的显式表达式.将方程(4)改写为
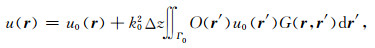
|
(12) |
式中薄板满足弱散射条件以确保Born近似的有效性,即速度扰动必须足够小,层的厚度也要尽量薄.我们注意到在Born近似的反演问题研究中[60],即使对于速度变化很大的多层介质(明显不符合小扰动假设条件),也有可能比较准确地估计反射强度和反射层位置.本文的研究将表明,对于单程波传播,通过引入其他的逼近假设,小扰动逼近的物理假设条件在很大程度上得到放宽.
将方程(6)代入方程(12),我们得到
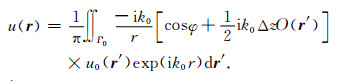
|
(13) |
相对于方程(6)所表示的常规Kirchhoff算子,方程(13)不仅包含了球面扩散因子、倾斜校正因子和子波整形因子,并且还包含了非均质薄板的相对慢度扰动.方程(13)为Born逼近单程波传播算子,其数值稳定性和计算精度有待下面的研究.其实,方程(13)表征的是一种条件稳定的单程波传播方程,其稳定性依赖于层厚、计算频率、传播角度及慢度扰动.对于有限带宽波场的单程传播,我们可以用下面的指数逼近:

|
(14) |
式中ψ=0.5k0ΔzO(r ′),带入方程(13)可以得到
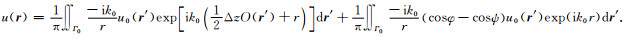
|
(15) |
此方程数值计算无条件稳定.二维情况下方程(15)变为
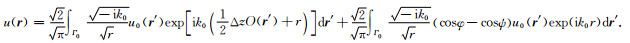
|
(16) |
方程(15)和(16)包含倾斜因子cosφ-cosψ,以校正速度扰动对传播角的影响.
指数逼近方程(14)使单程波传播无条件稳定,与传统相屏法中的小角度逼近
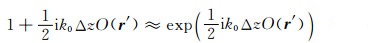
|
(17) |
相比,方程(14)可以应用于更大的传播角,其逼近精度与计算频率、薄板厚度和慢度有关.实际上,如果在单程波传播过程中忽略极大角度波的振幅变化,则方程(14)可以适用于更强的速度扰动和更大的传播角.下面我们计算指数逼近方程(14)所产生的相位和振幅误差,并与方程(17)的小角度逼近比较.设ψ(n)=0.5k0ΔxO(r′),方程(14)左边的振幅和相位分别为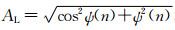
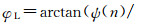
|
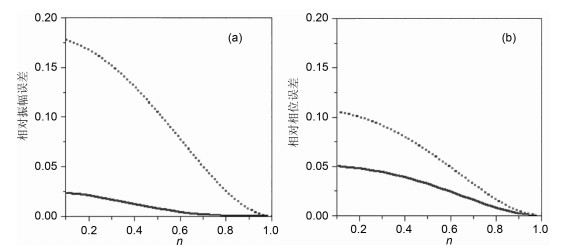
图 2 方程(14)(实线)和方程(17)(虚线)得到的相对振幅误差(a)和相位误差(b)随折射率的变化曲线 Fig. 2 Relative amplitude errors and phase errors caused respectively by equation (14)(solid line) and equation (17)(dotted line) and plotted versus the refractive index |
在单程波传播过程中,对于一个厚度较薄且Kirchhoff求和孔径有限的薄板,可以取cosφ≈ cosψ,这样方程(15)和(16)可改写为

|
(18) |
三维时:

|
(19) |
这种简化处理既可改善传统Kirchhoff传播算子,使之适用于非均匀介质情况,又保持了与后者相似的算法结构和计算时间.Fu[44]利用方程(18)和(19)发展了一种波场插值地震成像方法,即厚板波场外推加薄板插值的Fourier地震偏移成像方法,对盐丘等复杂地质构造模型进行了地震成像试验.
为了估计方程(15)计算单程波传播的精度,需要推导其频散关系.为简便起见,只考虑二维情况.对变量x进行Fourier变换(FT),并考虑如下的Green函数平面波展开表达式:
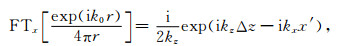
|
(20) |
则方程(15)变为
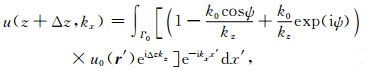
|
(21) |
其中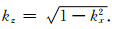
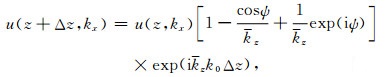
|
(22) |
其中正则化波数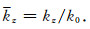
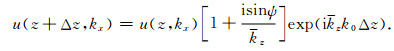
|
(23) |
上式为Born近似单程波传播算子波数域的一般表达式.假定背景场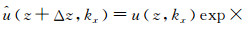
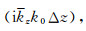
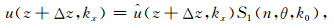
|
(24) |
其中θ为传播角度,一阶散射振幅函数为
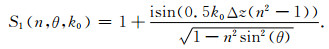
|
(25) |
很难看出方程(23)的频散关系,需要进一步的逼近处理.对于有限孔径薄板,我们可以使用如下指数近似:
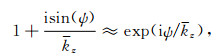
|
(26) |
将式(23)化简为
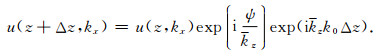
|
(27) |
此式仅考虑薄板波场延拓的相位变化,其频散关系可表示为
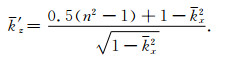
|
(28) |
可见,当n=1时(小扰动),有
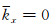
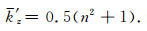
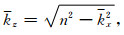
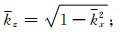
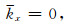
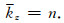

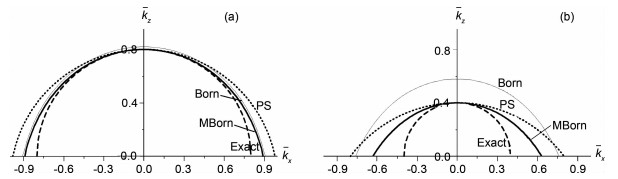
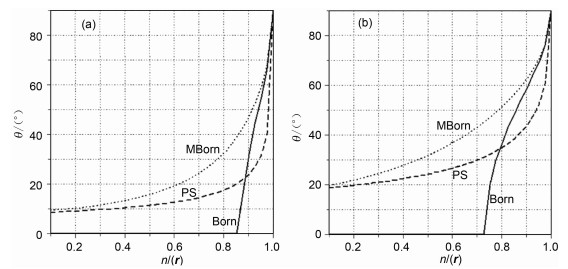
图 3所示为在弱速度扰动(n=0.8)和强速度扰动(n=0.4)两种情况下,由方程(28)计算得到的Born散射曲线(标示“Born”的细实线)与精确散射圆(标示“Exact”的短虚线)的对比图.可见,在弱速度扰动情况下Born散射曲线与精确散射圆相比误差很小;而在强速度扰动情况下则误差较大,这与前面的分析一致.图 4所示为根据公式(28)分别计算得到的在相对相位误差为1%和5%两种情况下的角谱曲线(即最大容许传播角度随折射率的变化曲线).结果表明,与相屏法角谱曲线(标示“PS”的短虚线)相比,Born法角谱曲线(标示“Born”的实线)在n=0.1~0.85时误差很大,只适用于小扰动近似(n=0.85~1.0).
|
图 3 精确频散圆(短虚线)与三种逼近方法的频散曲线比较 Born法(细实线),相屏法(点虚线)和修正Born法(粗实线),(a)弱速度扰动情况;(b)强速度扰动情况. Fig. 3 Comparison of the exact dispersion circle (dash line) with three approximate dispersion curves Born (thin line), phase-screen (dotted line), and modified Born (solid line), in the weak-contrast zone (a) and the strong-contrast zone (b). |
|
图 4 Born法(实线),相屏法(短虚线)和修正Born法(点虚线)逼近方法的角谱比较 (a)相对相位误差为1%情况;(b)相对相位误差为5%情况. Fig. 4 Comparison of angular spectra for three approximations:Born (solid line), phase-screen (dash line), and modified Born (dotted line) under the relative phase errors of 1%(a) and 5%(b). |
通过如下的相对慢度扰动简化,Born近似单程波传播算子的频散关系可得到极大的改善:
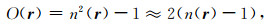
|
(29) |
该逼近使介质对比趋于平缓,将其代入式(28),可得到更精确的频散关系:
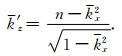
|
(30) |
可见,当n≈1时,有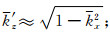
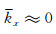
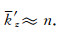
为了避免指数近似公式(26)对单程波传播算子相位精度分析的影响,我们不用频散方程,而是直接计算公式(23)的相位值:
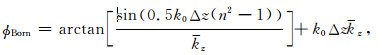
|
(31) |
与如下的精确相位值比较,
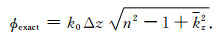
|
(32) |
定义相对相位误差为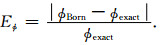

|
图 5 三种典型的折射率(分别代表弱对比n=0.95,中等对比n=0.65和强对比介质n=0.35)条件下,相屏传播算子(虚线)和方程(23)(实线)的相对相位误差随传播角的变化曲线 (a)使用方程(23),不用折射率平滑;(b)使用方程(23)和折射率平滑. Fig. 5 Comparison of relative phase errors for the phase-screen method (dotted line) and equation (23)(solid line) (a) Using equation (23) without the refractive-index smoothing; (b) Using equation (23) with the refractive-index smoothing.The relative phase errors are plotted as functions of propagation angles for three typical values of the refractive indexn=0.35, 0.65, and0.95, representing strong-contrast, moderate-contrast, and weak-contrast media, respectively. |
同样,可以通过折射率平滑来改善Born近似传播算子的相位精度,得到修正Born近似单程波传播算子.将方程(29)代入(31)得
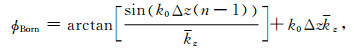
|
(33) |
其相对相位误差随传播角度的变化曲线如图 5b所示.可见与图 5a相比,折射率平滑极大地改善了传播算子的相位精度,对应所有的折射率值其相对相位误差皆小于相屏传播算子,特别是在中等对比区改善最明显.
上述分析表明,修正Born近似单程波传播算子将常规Kirchhoff传播算子的适用范围从横向均匀介质推广到速度中等程度对比的非均匀介质.其振幅和相位的逼近精度可以从如下的一阶散射振幅函数(公式(25)的改进)分析得到
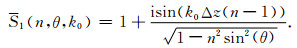
|
(34) |
虽然修正Born近似单程波传播算子比相屏传播算子具有更高的精度,适用于中等扰动和全局小角度波传播,但是由于该算子波数域版本在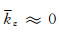
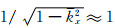
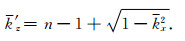
|
(35) |
使数值稳定的另一种途径是将波数域版本的修正Born近似单程波传播算子转化到空间域来数值实施.即将方程(29)代入(15)可得到方程(23)的空间域表达式:

|
(36) |
其中ψ=k0Δz(n(r ′)-1).基于方程(36)的空间域单程波传播因使用了传统Kirchhoff衍射求和,因此无条件稳定.总之,本文定义公式(36)为一阶Born-Kirchhoff传播算子,适用于非均匀介质的单程波传播计算,与适用于横向均匀介质的传统Kirchhoff传播算子相比,几乎不需要额外的计算时间.
3 高阶Born-Kirchhoff传播算子Lippmann-Schwinger积分方程(4)通过Born近似简化为一个显式的积分公式,进而导出一阶Born-Kirchhoff单程波传播算子,它实质上仅考虑薄板上边界Γ0的非均质对波场延拓的影响.为准确模拟单程波穿过非均匀薄板的传播效应,本章中我们使用矩形逼近来计算方程(4)中的体积分,得到一个比显式积分公式更准确的隐式积分方程,其对单程波传播算子的改善主要是在振幅方面.
用边界Γ0和Γ1上的两个面积分来近似计算方程(4)中的体积分,可得
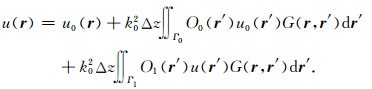
|
(37) |
上式右边前两项代表一阶Born-Kirchhoff显式解,用f(r)表示为
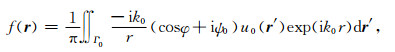
|
(38) |
或近似为
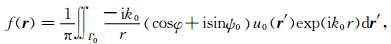
|
(39) |
式中ψ0=0.5k0Δz(n0(r ′)-1),其中n0(r′)表示Γ0面上的折射率.上式代入方程(37)并考虑三维问题,得到
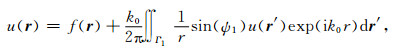
|
(40) |
式中ψ1=0.5k0Δz(n1(r
′)-1),其中n1(r′)表示Γ1面上的折射率.设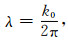
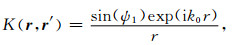
|
(41) |
则方程(40)可改写为一种标准的第二类Fredholm积分方程:

|
(42) |
其中r,r ′∈Γ1.方程(42)是一个隐式的波传播积分方程,求解该方程需要计算一个大矩阵的逆.我们首先评估方程(42)相对于显式方程(36)的改善之处.
假设Γ0和Γ1上的折射率都是常数,分别为n0和n1,是Γ0和Γ1上折射率的平均值.采用类似于其他波数域传播算子的推导方法[36, 44],通过Fourier变换将方程(42)变换到波数域:
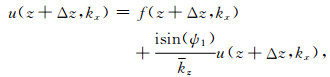
|
(43) |
其中f(z+Δz,kx)是从(38)式的Fourier变换得到
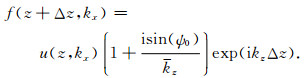
|
(44) |
代入方程(43)得
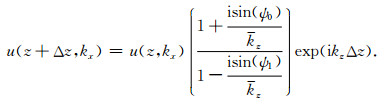
|
(45) |
上述方程是隐式积分方程(42)的波数域形式,其中方括号项数学上是一种稳定的隐式结构,从振幅方面改善单程波穿过非均匀薄板的传播,比一阶Born-Kirchhoff单程波传播算子中的不稳定显式结构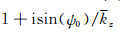
|
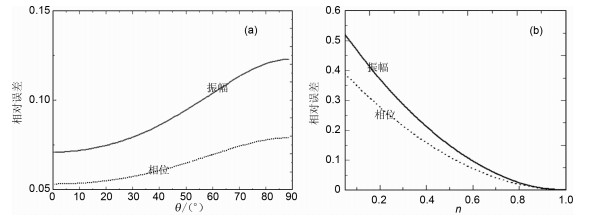
图 6 隐式和显式传播算子间的相对振幅(实线)和相对相位(虚线)误差 (a)n=0.65时,该误差关于传播角的变化曲线;(b)传播角为20°时,该误差关于折射率的变化曲线. Fig. 6 Relative amplitude (solid line) and phase (dotted line) errors between the implicit and explicit propagators are plotted (a) Versus propagation angles atn=0.65;(b) Versus the refractive index at a propagation angle of 20°. |
虽然方程(45)是数值稳定的,但是它不符合当前的相屏算法框架,需要对方程做一些必要的简化,比如对于相邻薄板之间速度差异不太大的情况,我们可以假设
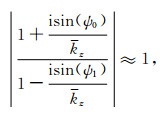
|
(46) |
这样方程(45)简化为
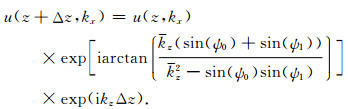
|
(47) |
对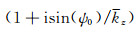
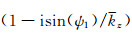
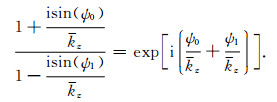
|
(48) |
方程(48)代入方程(45),根据方程(46)可以假定ψ0=ψ1,从而可以导出修正的Born频散方程(30).考虑ψ0≈ψ1,隐式方程(45)的散射振幅表达式为

|
(49) |
通过配置方法可以数值求解隐式积分方程(42),进行地震正演模拟[48].当r趋于r′时,积分核奇异,但是它可去奇点[49],所以K(r,r ′)和f(r)在Γ1上连续.从积分核K(r,r′)中1/r的衰减特性可知,利用菲涅耳带选取最佳孔径进行积分计算,得到的数值矩阵是稀疏的.由于配置法需要大规模的数值计算,比单程波方法耗费计算资源,必须在计算效率和计算精度之间作平衡.
多年来,迭代求解积分方程(42)得到了广泛的研究,利用Born序列逼近,隐式积分方程(42)可以表示为显式求和过程:
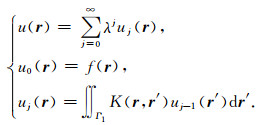
|
(50) |
为了研究Born序列逼近的收敛性,我们假定连续函数K(r,r ′)和f(r)在Γ1上的极大值为
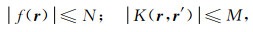
|
(51) |
进而得到
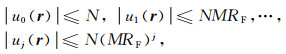
|
(52) |
其中RF是积分孔径.公式(50)中Born序列收敛的条件是其相邻两求和项之比小于1,即

|
(53) |
这等价于
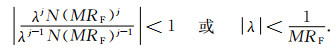
|
(54) |
为了方便精度分析和算法实施,我们将公式(50)改写为迭代核的求和:
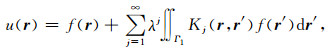
|
(55) |
其中各阶迭代核可表示为
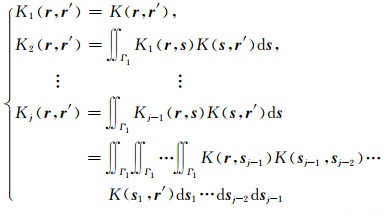
|
(56) |
从方程(51)和(56)可知

|
(57) |
即只要λ满足方程(54),那么Born序列解(55)式是收敛的.
为了方便分析Born序列解(55)式的逼近精度和收敛特性,我们对方程(55)两边做二维Fourier变换,得到其波数域的版本:
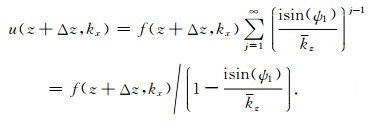
|
(58) |
方程(44)代入方程(58)得到方程(45),表明上述显式的Born序列无穷级数解收敛到最终的隐式解.在实际应用中,通常需要对Born序列截断,取有限项计算,涉及逼近精度和收敛特性的分析.假定采用J阶Born序列逼近,方程(58)重写为
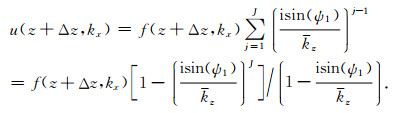
|
(59) |
相应的得到
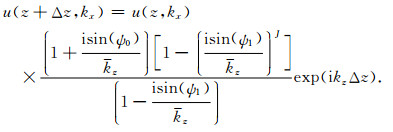
|
(60) |
这就是高阶Born-Kirchhoff单程波传播算子的波数域表达式.
通过比较各阶Born序列显式解方程(60)与隐式解方程(45)之间的振幅和相位误差,可以分析非均质薄板各阶Born-Kirchhoff单程波传播算子的逼近确度.隐式解方程(45)和Born序列显式解方程(60)的振幅和相位分别表示为
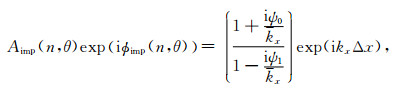
|
(61) |
和
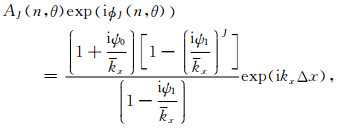
|
(62) |
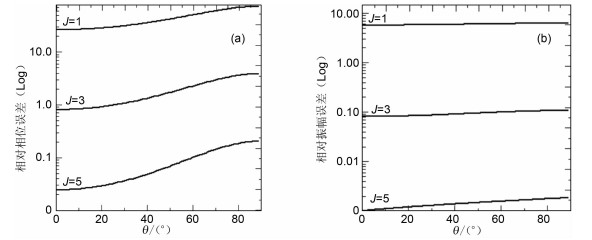
式中θ为传播角.各阶Born序列显式解的逼近精度分析可以通过计算Aimp(n,θ)与AJ(n,θ)之间的相对振幅误差和Φimp(n,θ)与ΦJ(n,θ)之间的相对相位误差来实现.取k0Δz=1,图 7和图 8分别绘出了相对振幅和相位误差随传播角和折射率的变化曲线.可见,Born序列显式解的低阶项收敛快速,随着阶数增加,逼近误差非线性地减小.
|
图 7 各阶Born序列显式解方程(60)与隐式解方程(45)之间的相对相位误差(a)和相对振幅误差(b)随传播角的变化曲线 Fig. 7 Relative phase (a) and amplitude (b) errors between the implicit propagator and different order operators of the Born series approximation are plotted versus propagation angles |
|
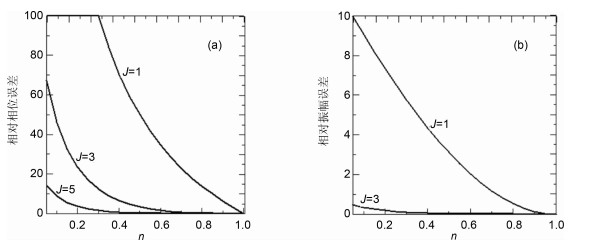
图 8 各阶Born序列显式解方程(60)与隐式解方程(45)之间的相对相位误差(a)和相对振幅误差(b)随折射率的变化曲线 Fig. 8 Relative phase (a) and amplitude (b) errors between the implicit propagator and different order operators of the Born series approximation are plotted versus the refractive index. |
对给定的波传播允许误差限e,我们可以通过解下列方程得到n-θ函数关系
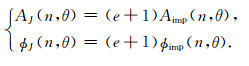
|
(63) |
传统的Kirchhoff传播算子可以通过两种方式进行数值实施:高精度的逐层递推方式和高计算效率的非递推方式.Kirchhoff求和过程首先沿衍射双曲面对地震数据进行球面扩散补偿、倾斜因子和子波整形因子校正,然后进行叠加.一阶和高阶的Born-Kirchhoff传播算子采用同样的求和技术进行数值实施,只是在地震数据求和之前进行额外振幅和相位校正,以补偿由于速度横向扰动引起的误差.同样可以采用有限孔径的逐层递推数值实施,上一个延拓步的输出作为下一个延拓步的输入,每一层的波场延拓计算可以选用一个适应局部速度场的背景速度,从而降低薄板内的速度对比.
下面我们对Born-Kirchhoff传播算子的被积函数采用矩阵离散表示.考虑二维问题,我们将整个不均匀介质模型沿波的传播方向以Δz间隔离散成M个薄板,对每个薄板沿着x方向以Δx间隔离散成N个点.对于波场向前递推穿过第L个薄板时,一阶Born-Kirchhoff传播方程(42)被离散为
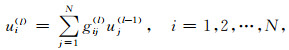
|
(64) |
其中uj(l-1)是薄板上边界的空间离散波场,即输入波场;ui(l)是薄板下边界的波场,即输出波场;gij(l)是一个以频率、速度、薄板厚度为函数的复系数,可以按如下公式计算
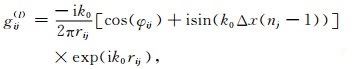
|
(65) |
其中
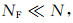
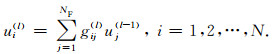
|
(66) |
此外,背景波数k0可以选用孔径范围NF内的局部波数,而不需要用整个孔径范围N内的整体波数.这样每次利用公式(66)进行Kirchhoff求和时,只需用局部速度计算背景波数.这种变k0方法能降低薄板内的速度对比.公式(66)用矩阵形式表示为
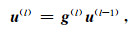
|
(67) |
其中g(l)是一个(N×NF)阶的稀疏传播矩阵.重复进行上述迭代过程,使波场穿过所有薄板,得到
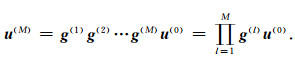
|
(68) |
对于二阶Born-Kirchhoff传播算子,对公式(55)取其二阶表达式,利用上述的方法离散为
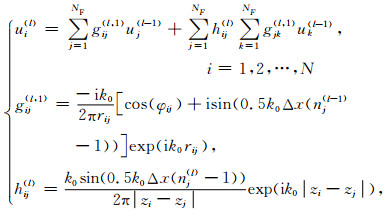
|
(69) |
令
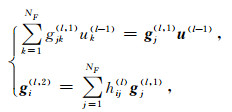
|
(70) |
得到公式(69)的矩阵表达形式
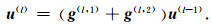
|
(71) |
同样的数值离散推导过程可以推广应用到m阶Born-Kirchhoff传播算子,得到
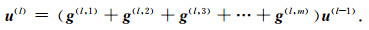
|
(72) |
因为薄板内为非均匀介质,产生的复矩阵是不对称的.显然,高阶Born-Kirchhoff传播算子的数值实施涉及大量的矩阵运算.
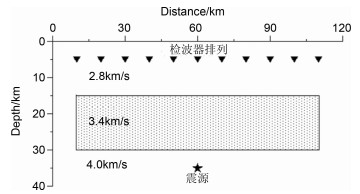
为了检验本文提出的Born-Kirchhoff传播算子的精度,我们给出了一个单程波数值模拟的例子.将单程波数值模拟结果和全波的边界元法模拟[62]结果进行了对比.图 9所示为一个简单的二维速度模型和观测系统示意图.模型为层内均匀的三层速度,速度值在图中标出.检波点布设于第一层顶面,共101道,道间距1 km.炮点位于第三层,子波为高斯函数的导数,计算频率为0~2.5 Hz.我们主要模拟和观测穿过中间层的地震单程波能量.在模拟过程中,第一层和第三层的速度保持不变,速度扰动只集中在中间层.图 10a为全波边界元法计算的合成地震图.然后,对中间层在平均3400 m/s速度基础上加20%的速度扰动,使该层的最小速度变为2720 m/s.分别利用常规Kirchhoff和一阶Born-Kirchhoff传播算子计算合成地震图,结果如图 10b和图 10c所示.对比这三种数值模拟结果可见,波形总体上是一致变化的,表明在一定的传播距离内,单程波传播方法在一定程度上可以模拟波形的变化.进一步的研究表明在单程波模拟结果中,异常的波形畸变与地震波中的小尺度能量分布密切相关[17].图 10的简单计算例子表明,Born-Kirchhoff单程波传播算子在一定的传播距离内可以保持小尺度能量成份的相对变化.
|
图 9 简单二维模型的速度结构和观测系统 中间层使用了20%的速度扰动测评Born-Kirchhoff算子与全波形边界元法的优劣. Fig. 9 The velocity structure and observation configuration of a simple 2-D model A 20% velocity perturbation is used in the intermediate layer to test the Born-Kirchhoff propagators against the full-waveform boundary-element method |

|
图 10 对图 9中间层在平均3400 m/s速度基础上加20%的速度扰动,然后利用全波边界元法(a)、常规Kirchhoff单程波传播算子(b)和一阶Born-Kirchhoff单程波传播算子(c)分别计算的合成地震图 Fig. 10 Synthetic seismograms for the model in Figure 9, calculated by the boundary-element method (a), the first-order Born-Kirchhoff propagator (b), and the conventional Kirchhoff propagator (c) |
这三种方法模拟结果最大的不同表现在初至时间上,这是因为单程波方法用了不同的近似方法而产生的.传统Kirchhoff方法适用于横向均匀的层状介质,其结果(图 10b)初至明显滞后;而一阶Born Kirchhoff方法适用于中等程度的速度横向变化(图 10c),其结果初至时间与全波的边界元法计算结果相差很小.我们在前面提到Born-Kirchhoff传播算子精度随着传播角度的增大而增大(见图 6).图 11比较了常规Kirchhoff算子(虚线)和一阶Born-Kirchhoff算子(实线)的相对走时误差,走时误差的计算首先逐道计算单程波和边界元法双程波之间的误差,再用边界元法双程波走时进行规一化处理.可见与预期的一致,常规Kirchhoff法的相对相位误差远大于一阶Born-Kirchhoff法.Born近似的相对相位误差随着偏移距(传播角度)的增加而明显增大,尤其是偏移距超出一定的范围之后.

|
图 11 常规Kirchhoff法(虚线)和一阶Born-Kirchhoff法(实线)合成地震记录与双程波边界元法合成地震记录之间的相对走时误差 Fig. 11 Relative traveltime errors between the boundary-element method and the conventional Kirchhoff (dotted line)/first-order (solid line) Born-Kirchhoff propagators, calculated from the synthetic seismograms in Figure 10. |
本文基于Lippmann-Schwinger积分公式将传统的Kirchhoff单程波传播算子推广适用于横向速度变化的非均匀介质,考虑了波在非均匀介质中传播时,非均匀体的散射作用对单程波传播的影响.由此得到的Born-Kirchhoff单程波传播算子比目前在用的Ray-Kirchhoff单程波传播算子在振幅和相位两方面具有更高的计算精度.基于Born序列逼近,我们导出了各阶Born-Kirchhoff单程波传播算子的显式和隐式表达式,并进行了详细的精度分析,以刻画这些算子对传播角度和介质非均质的尺度依赖特征.主要的结论总结如下.
利用Born近似和Born序列近似将描述双程波传播的Lippmann-Schwinger积分方程简化为单程波的积分表达式.由此得到的Born-Kirchhoff单程波传播算子由于折射率平滑近似而不必局限于Born小扰动假设的限制.单程波近似通常会破坏波在非均匀介质中传播的振幅平衡,导致传播算子在波数域数值计算的不稳定.本文的研究表明这些算子在空间域进行数值计算是无条件稳定的.利用Born序列频散方程,可以定量分析各阶Born-Kirchhoff单程波传播算子描述波在非均匀介质中传播的精度,研究表明Born-Kirchhoff单程波传播算子对强非均匀介质和大传播角度的适应性比相屏法或SSF法明显提高.
我们分别用传统Kirchhoff单程波传播算子和一阶Born-Kirchhoff单程波传播算子对一个简单的层状模型进行合成地震图计算,并与全波边界元法计算结果进行对比.结果表明对于非均匀介质,一阶Born-Kirchhoff单程波算子能很好保持波形的相对变化,其相位误差比传统Kirchhoff单程波算子明显减小.
| [1] | Born M. Optic. Springer Publ.Co.Inc , 1933. |
| [2] | Kennett B L N. Seismic waves in laterally varying media. Geophys.J.Roy.Astr.Soc , 1972, 27: 310-325. |
| [3] | Hudson J A, Humphryes R F, Mason I M, Kembhavi V K. The scattering of longitudinal elastic waves at a rough free surface. J.Phys.D:Appl.Phys , 1973, 6: 2174-2186. DOI:10.1088/0022-3727/6/18/303 |
| [4] | Snieder R, Nolet G. Linearised scattering of surface waves on a spherical earth. J.Geophys , 1987, 61: 55-63. |
| [5] | Cohen J K, Bleistein N. Velocity inversion procedure for acoustic waves. Geophysics , 1979, 44: 1077-1087. DOI:10.1190/1.1440996 |
| [6] | Clayton R W, Stolt R H. A Born-WKBJ inversion method for acoustic reflection data. Geophysics , 1981, 46: 1559-1567. DOI:10.1190/1.1441162 |
| [7] | Wu R S, TokaOz M N. Diffration tomography and multisource holography applied to seismic imaging. Geophysics , 1987, 52: 11-25. DOI:10.1190/1.1442237 |
| [8] | Snieder R. Large-scale waveform inversions of surface waves for lateral heterogeneity-Ⅰ.Theory and numerical examples. J.Geophys.Res , 1988, 93: 12055-12066. DOI:10.1029/JB093iB10p12055 |
| [9] | Coates R T, Chapman C H. Generalized Born scattering of elastic waves in 3-D media. Geophys.J.Int , 1991, 107: 231-263. |
| [10] | Knopoff L, Hudson J A. Scattering of elastic waves by small inhomogeneitiea. J.Acoust.Soc.Am , 1964, 36: 338-343. DOI:10.1121/1.1918957 |
| [11] | Sato H. Attenuation of body waves and envelope formation of three-component seismograms of small local earthquakes in randomly inhomogeneous lithosphere. J.Geophys.Res , 1984, 89: 1221-1241. DOI:10.1029/JB089iB02p01221 |
| [12] | Wu R S, Aki K. Elastic wave scattering by a random medium and the small-scale inhomogeneities in the Lithosphere. J.Geophys.Res , 1985, 90: 10261-10273. DOI:10.1029/JB090iB12p10261 |
| [13] | Flatté S M, Wu R S. Small-scale structure in the Lithosphere and asthenosphere deduced from arrival time and amplitude fluctuations. J.Geophys.Res , 1988, 93: 6601-6614. DOI:10.1029/JB093iB06p06601 |
| [14] | Hudson J A, Heritage J R. The use of the Born approximation in seismic scattering problems. Geophys.J.Roy.Astr.Soc , 1982, 66: 221-240. |
| [15] | Bleistein N, Cohen J K, Stockwell Jr J W. Mathematics of Multidimensional Seismic Imaging, Migration, and Inversion. New York: Springer-Verlag Inc, 2000 . |
| [16] | Sato H, Fehler M C. Seismic wave propagation and scattering in the heterogeneous earth. Springer , 1998. |
| [17] | Fu L Y, Wu R S, Campillo M. Energy partition and attenuation of regional phases by random free surface. Bulletin of the Seismological Society of America , 2002, 92: 1992-2007. DOI:10.1785/0120000292 |
| [18] | Carter J A, Frazar L N. Accommodating lateral velocity changes in Kirchhoff migration by means of Fermat' s principle. Geophysics , 1984, 49: 46-53. DOI:10.1190/1.1441560 |
| [19] | Vidale J. Finite-difference calculation of travehimes. Bull.Seis.Soc.Am , 1988, 78: 2062-2076. |
| [20] | Keho T H, Beydoun W B. Paraxial ray Kirchhoff migration. Geophysics , 1988, 53: 1540-1546. DOI:10.1190/1.1442435 |
| [21] | Hill N R. Gaussian beam migration. Geophysics , 1990, 55: 1416-1428. DOI:10.1190/1.1442788 |
| [22] | Moser T. Shortest path calculation of seismic rays. Geophysics , 1991, 56: 59-67. DOI:10.1190/1.1442958 |
| [23] | 徐昇, 杨长春, 刘洪, 等. 射线追踪的微变网格方法. 地球物理学报 , 1996, 39(1): 97–102. Xu S, Yang C C, Liu H, et al. A grid-changeable method for ray tracing. Chinese J.Geophys (in Chinese) , 1996, 39(1): 97-102. |
| [24] | 张建中, 陈世军, 徐初伟. 动态网格最短路径射线追踪. 地球物理学报 , 2004, 47(5): 899–904. Zhang J Z, Chen C J, Xu C W. A method of shortest path raytraeing with dynamic networks. Chinese J.Geophys (in Chinese) , 2004, 47(5): 899-904. |
| [25] | Zhang M, Chen B, Li X, et al. A fast algorithm of shortest path ray tracing. Chinese J.Geophys , 2006, 49: 1467-1474. |
| [26] | Gray S H, Etgen J, Dellinger J, et al. Seismic migration problems and solutions. Geophysics , 2001, 66: 1622-1640. DOI:10.1190/1.1487107 |
| [27] | Woodward M J. Wave-equation tomography. Geophysics , 1992, 57: 15-26. DOI:10.1190/1.1443179 |
| [28] | Stoffa P L, Fakkema J T, de Luna Freire R M, et al. Splitstep Fourier migration. Geophysics , 1990, 55: 410-421. DOI:10.1190/1.1442850 |
| [29] | Fisk M D, McCartor G D. The phase screen method for vector elastic waves. J.Geophys.Res , 1991, 96: 5985-6010. DOI:10.1029/91JB00201 |
| [30] | Wu R S. Synthetic seismogram in heterogeneous media by one-return approximation. Pure and Applied Geophys , 1996, 148: 155-173. DOI:10.1007/BF00882059 |
| [31] | Huang L J, Fehler M C, Wu R S. Extended local BornFourier migration method. Geophysics , 1999, 64: 1524-1534. DOI:10.1190/1.1444656 |
| [32] | Jin S, Wu R S, Peng C.Prestack depth migration using a hybrid pseudo-screen propagator.68th Ann.Internat.Mtg., Soc.Expl.Geophys, Expanded Abstract s, 1998, 1819-1822 |
| [33] | Wu R S, Jin S, Xie X B. Seismic wave propagation and scattering in heterogeneous crustal wave guides using screen propagators-1.SH waves. Bull.Seism.Soc.Am , 2004, 90: 401-413. |
| [34] | de Hoop M V, Le Rousseau J H, Wu R S. Generalization of the phase-screen approximation for the scattering of acoustic waves. Wave Motion , 2000, 31: 43-70. DOI:10.1016/S0165-2125(99)00026-8 |
| [35] | Fu L Y, Duan Y.Fourier depth migration methods with application to salt-related complex geological structures.72th Ann.Internat.Mtg., Soc.Expl.Geophys, Expanded Abstracts, 2002.895-898 |
| [36] | Fu L Y. Comparison of different one-way propagators for wave forward propagation in heterogeneous crustal wave guides. Bull.Seism.Soc.Am , 2006, 96: 1091-1113. DOI:10.1785/0120050159 |
| [37] | Fu L Y, Sun W J, Li D P. Degenerate fourier migrators for imaging complex fault zones. Chinese J.Geophys , 2007, 50: 483-495. DOI:10.1002/cjg2.v50.2 |
| [38] | Collins M D. A split-step Pads solution for the parabolic equation method. J.Acoust.Soc.Am , 1993, 93: 1736-1742. DOI:10.1121/1.406739 |
| [39] | Ristow D, Ruhl T. Fourier finite-difference migration. Geophysics , 1994, 59: 1882-1893. DOI:10.1190/1.1443575 |
| [40] | Wu R S. Wide-angle elastic wave one-way propagation in heterogeneous media and an elastic wave complex-screen method. J.Geophys.Res , 1994, 99: 751-766. DOI:10.1029/93JB02518 |
| [41] | Wild A J, Hudson J A. A geometrical approach to the elastic complex screen. J.Geophys.Res , 1998, 103: 707-725. DOI:10.1029/97JB02757 |
| [42] | Hobbs R W. 3-D modelling of seismic wave propagation using complex elastic screens with application to mineral exploration.Special Volume on Hardrock Geophysics, Soc. Expl.Geophys.Publisher , 2003. |
| [43] | Fu L Y.Born dispersion equation and Kirchhoff migration in laterally heterogeneous media.72th Ann.Internat.Mtg., Soc.Expl.Geophys, Expanded Abstract s, 2002.1097 1100 |
| [44] | Fu L Y. Wavefield interpolation in the Fourier wavefield extrapolation. Geophysics , 2004, 69: 257-264. DOI:10.1190/1.1649393 |
| [45] | Schuster G T. A hybrid BIE+Born series modeling scheme:Generalized Born series. J.Acoust.Soc.Am , 1985, 77: 865-879. DOI:10.1121/1.392055 |
| [46] | Schuster G T. Solution of the acoustic transmission problem by a perturbed Born series. J.Acoust.Soc.Am , 1985, 77: 880-886. DOI:10.1121/1.392056 |
| [47] | Fu L Y. Rough surface scattering:Comparison of various approximation theories for 2D SH waves. Bull.Seism.Soc.Am , 2005, 95: 646-663. DOI:10.1785/0120040081 |
| [48] | Fu L Y, Bouchon M. Discrete wavenumber solutions to numerical wave propagation in piecewise heterogeneous media-Ⅰ.Theory of two-dimensional SH case. Geophys.J.Int , 2004, 157: 481-498. DOI:10.1111/gji.2004.157.issue-2 |
| [49] | Fu L Y, Mu Y G, Yang H J. Forward problem of nonlinear Fredholm integral equation in reference medium via velocityweighted wavefield function. Geophysics , 1997, 62: 650-656. DOI:10.1190/1.1444173 |
| [50] | Fu L Y, Wu R S. Infinite boundary element absorbing boundary for wave propagation simulations. Geophysics , 2000, 65: 625-637. |
| [51] | Berkhout A J, Wapenaar C P A. One-way versions of the Kirchhoff integral. Geophysics , 1989, 54: 460-467. DOI:10.1190/1.1442672 |
| [52] | Hilterman F J. Three dimensional seismic modeling. Geophysics , 1970, 35: 1020-1037. DOI:10.1190/1.1440140 |
| [53] | Trorey A W. A simple theory for seismic diffractions. Geophysics , 1970, 35: 762-784. DOI:10.1190/1.1440129 |
| [54] | French W S. Computer migration of oblique seismic reflection profiles. Geophysics , 1975, 40: 6-16. DOI:10.1190/1.1440516 |
| [55] | Schneider W A. Integral formulation for migration in two and three dimensions. Geophysics , 1978, 43: 49-76. DOI:10.1190/1.1440828 |
| [56] | Safar M H. On the lateral resolution achieved by Kirchhoff migration. Geophysics , 1985, 50: 1091-1099. DOI:10.1190/1.1441981 |
| [57] | Yilmaz O. Seismic data processing.Soe.Expl. Geophys.Publisher , 1987. |
| [58] | Hubral P, Sehleicher J, Tygel M, Hanitzseh C. Determination of Fresnel zones from traveltime measurements. Geophysics , 1993, 58: 703-712. DOI:10.1190/1.1443454 |
| [59] | Schleicher J, Hubral P, Tygel M, et al. Minimum apertures and Fresnel zones in migration and demigration. Geophysics , 1997, 62: 183-194. DOI:10.1190/1.1444118 |
| [60] | Bleistein N, Cohen J K, Stockwell Jr J W. Mathematics of Multidimensional Seismic Imaging, Migration, and Inversion. New York: Springer-Verlag Inc, 2000 . |
| [61] | Huang L J, Fehler M C. Accuracy analysis of the split-step Fourier propagator:implications for seismic modeling and migration. Bull.Seism.Soc.Am , 1998, 88: 18-29. |
| [62] | Sdnchez-sesma F J, Campillo M. Topographic effects for incident P, SV and Rayleigh waves. Tectonophysics , 1993, 218: 113-125. DOI:10.1016/0040-1951(93)90263-J |
 2010, Vol. 53
2010, Vol. 53

