2. 中国地震局地壳应力研究所, 100089 北京
2. Institute of Crustal Dynamics, China Earthquake Administration, 100089 Beijing, China
地幔对流被认为是地球内部热传递的最有效方式和地表板块运动的动力源[1], 而地幔流变性是影响热传递和地幔对流状态和格局的关键因素[2, 3].在地幔对流的研究中, 常采用的黏度结构主要为两种:第一种是常黏度或仅随径向(深度)变化的黏度; 第二种是仅随温度或同时随温度和压力变化的黏度.第一种黏度结构比较简单, 利用之仅能获得地幔对流的极型场, 主要揭示了地幔物质上下运移特征和规律, 对解释地表板块在洋中脊处的发散运动、俯冲带和碰撞带处的汇聚运动, 甚至观测到的地球物理场发挥了重要的作用[4~7].然而, 在齐次边界条件下, 利用这种黏度结构获得的地幔对流场无法解释地表板块旋转与走滑运动.实验和理论研究[8, 9]表明, 地幔黏度强烈依赖于温度和压力.一般情况下, 地幔温度同时存在径向变化和横向变化, 因此第二种黏度结构中同时包含了两部分:剧烈的径向黏度变化[10, 11]和强烈的横向黏度变化[12].地幔横向黏度变化的引入, 不仅会对对流状态和格局、相变动力学、地球内部热结构和板块动力学产生巨大的影响[13~23], 而且即使在均匀边界下, 也能够自然地获得环型场分量.虽然其速度大小仅占总速度场的几个百分点, 但是由于其能量主要存在于地幔浅部[13, 24], 而且在局部区域, 在地表附近的上升热柱的正上方或附近, 环型运动速度可以达到极型速度场的35%或更高[25, 26], 可能会对大地水准面异常、重力异常和地形起伏产生重要的影响[27~32].大量的研究结果[13, 16~19, 33~35]表明, 径向黏度变化对对流格局起控制作用, 而横向黏度变化则起辅助的调节作用.在这些研究中, 采用了随温度变化的黏度结构, 这样就难以进一步认识和理解横向黏度变化对地幔对流的影响.要达到这个目的, 需将横向黏度变化从径向黏度变化中分离出来.因此, 本文不采用温度依赖的黏度结构, 而是在径向黏度不变的情况下, 加入一个强度可以变化的横向黏度变化项, 来从理论上研究其对球层中热对流的影响.
2 基本方程及求解方法 2.1 基本方程考虑内径为R1, 外径为R2的充满了不可压缩的牛顿流体的同心球层, 纯粹从球层底部加热, 采用Boussinesq近似, 并取流体的普朗特数为无限大(Pr=ν/κ, ν为运动学黏度; κ为热扩散系数.地球地幔的普朗特数约1024[36]), 球层中流体的黏度为流体平均黏度η0加上横向黏度变化η珓.在球坐标系(r, θ, φ)中, 控制变黏度流体运动的无量纲方程组可表述为

|
(1a) |
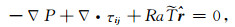
|
(1b) |

|
(1c) |
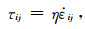
|
(1d) |
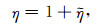
|
(1f) |
在式(1a)~(1f)中, 采用了无量纲化因子:球层厚度d=R2-R1, κ/d, d2/κ, ΔT=T1-T2和η0分别对半径r, 速度u, 时间t, 温度和黏度进行了无量纲化.其中, T1, T2分别为内径R1, 外径R2处的恒定温度, T1>T2; P为压力; Tc是无对流运动时的温度场, 仅是径向r的函数, 满足热传导方程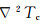
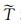
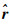

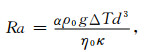
|
(2) |
其中, α, ρ0和g分别为球层中流体的热膨胀系数, 流体平均密度和重力加速度.
将速度场u分解为标量极型场Φ和环型场ψ[37], 然后在式(1b)两端分别施加运算
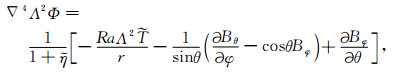
|
(3a) |

|
(3b) |
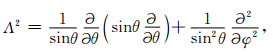
|
(3c) |
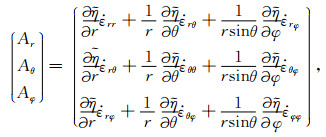
|
(3d) |
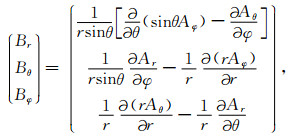
|
(3e) |
可以看出, 式(3a)和(3b)比小横向黏度变化情况下[25]均多了一项
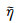
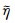
本文仅研究上边界为刚性等温边界、下边界为应力自由等温边界的情形, 其数学形式为:
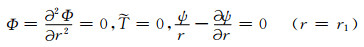
|
(4a) |
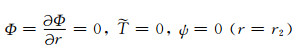
|
(4b) |
在此, 仿照朱涛和冯锐[24], 在不失横向黏度变化的动力学意义下, 可以假定横向黏度具有如下的随余纬度变化的形式:
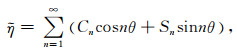
|
(5) |
其中Cn和Sn为给定或已知的系数.若取基阶即主要部分进行计算, 此时
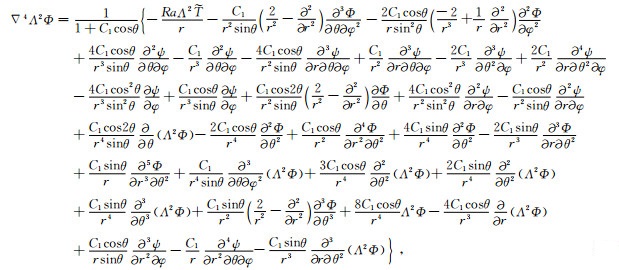
|
(6a) |
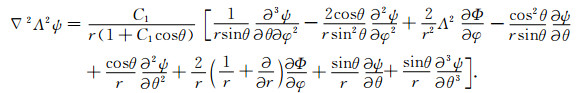
|
(6b) |
至此, 式(6)、(1c)和边界条件(4)构成了求解横向黏度仅随余纬度变化下的极型场和环型场的方程组.
2.3 求解方法 2.3.1 球谐函数展开
假定极型场标量函数Φ、环型场标量函数ψ、黏度扰动
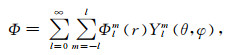
|
(7a) |
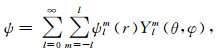
|
(7b) |
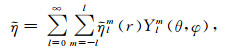
|
(7c) |
其中, Ylm(θ, φ)是正规化的l阶m级面谐函数, 形式为
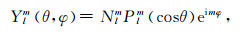
|
(8) |

|
(9) |
其中, Plm(cosθ)是正规化的l阶m级的缔合勒让德函数.面谐函数的正交归一关系为

|
(10) |
其中, Yl*m是Ylm的共轭.
将式(7)带入式(6)和式(4)可得
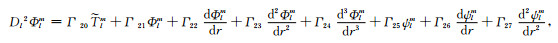
|
(11a) |

|
(11b) |
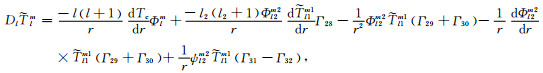
|
(11c) |
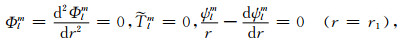
|
(11d) |
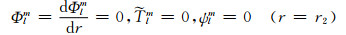
|
(11e) |
其中, 
式(11)是l≠0情况下计算极型场和环型场分量的方程组.从式(11a)~(11c)可以看出, 环型场和极型场的不同波长的分量是相互耦合的, 它们的耦合程度由与黏度横向变化大小C1有关的系数Γi来控制.当l=0时, 式(11a)和(11b)变为
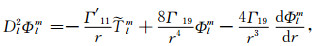
|
(12a) |
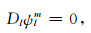
|
(12b) |
显然, 环型场为零, 但式(12a)比常黏度模型多了两项(右端第二和第三项), 也就是说, 在横向变化黏度存在的情况下, 零阶极型场不再只由热浮力源产生.
2.3.2 Galerkin近似Galerkin方法是将连续问题转换为离散问题的一种方法.Zebib等[38]、叶正仁等[39]以及朱涛和冯锐[40]将之用来求解地幔对流模型.在此, 也采用Galerkin方法来进行求解式(11).设
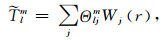
|
(13a) |

|
(13b) |
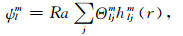
|
(13c) |
取基函数

|
(14) |
则Θljm自然满足关于温度的边界条件.将式(13)和(14)带入式(11)和(12), 并利用三角函数的正交性可得
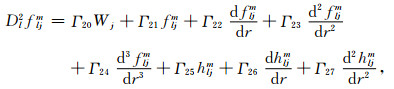
|
(15a) |

|
(15b) |
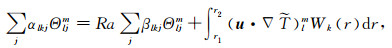
|
(15c) |
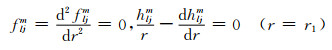
|
(15d) |
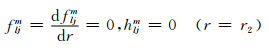
|
(15e) |
其中,
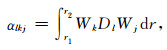
|
(16a) |
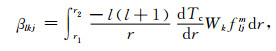
|
(16b) |
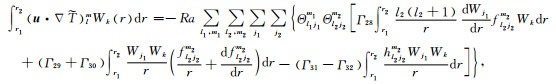
|
(16c) |
当l=0时, 式(12a)变为
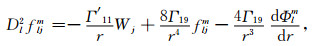
|
(17) |
从式(15)和(16)可以看出, 先利用式(15a)或(17)、(15b)、(15d)、(15e)可获得fljm和hljm, 然后便归结为求解关于Θljm的非线性方程组(15c).
3 数值方法及程序验证对于式(15)和(16)的数值离散, 文中采用有限差分方法.具体离散方法:对一阶和三阶偏微分采用向前差分格式, 对二阶和四阶则采用向后差分格式.对非线性方程组(15c)采用Levenberg-Marquardt方法[41]进行求解, 迭代格式为

|
(18) |
其中, 
本文采用两种方式来验证程序计算结果的可靠性.第一, 采用与解析方法LSA (linearstability analysis)获得的临界瑞利数Racr进行对比的方式来验证本文所用的程序代码.验证时使用的模型[15]为:等黏度球层模型, 纯粹从底部加热, 上下均为应力自由等温边界, 球层内径为0.5, 外径为1.0.文中取Galerkin最大求和项数为6, 对式(16a)和(16b)的积分步长为0.005.忽略非线性方程组(15c)中的非线性项后, 计算得到的各阶l的临界瑞利数见表 1.表 1中的第三行值是根据文献[15]提供的结果换算得到的.第二, 通过程序计算获得上下边界层处的Nussult数Nu, 然后与文献[15]提供的结果进行比较.验证时使用的模型[15]为:等黏度球层模型, 纯粹从底部加热, 上下均为应力自由等温边界, 球层内径为0.55, 外径为1.0.结果见表 2.
|
|
表 1 临界瑞利数Racr Table 1 Critical Rayleigh number Racr |
|
|
表 2 Nussult数的比较(Ra=7000) Table 2 Comparison of Nussult number (Ra=7000) |
从表 1看出, 利用本文的程序计算的临界瑞利数与解析方法获得的值相差很小, 除一阶(1.63%)和二阶(1.13%)的误差大于1.0%外, 其余均小于1.0%.从表 2可以看出, 本文计算的Nu数虽然比文献[15]的结果大一些, 但与文献[15]的结果还是比较接近的, 这表明本文的程序是可靠的.
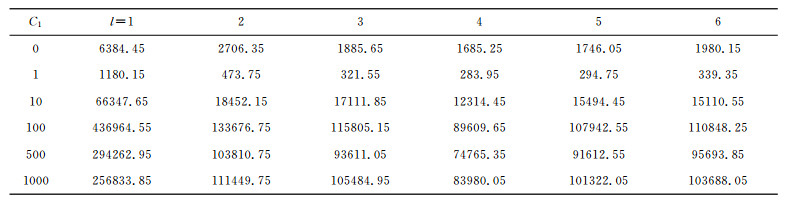
4 计算结果及分析在研究中, 球谐展开的最大阶数取lmax=6, 同时取jmax=kmax=6, 以及R1=3471km, R2=6271km, 它们分别对应于核幔边界和岩石圈底界面的位置.全地幔瑞利数的量级约为107[36], 因此计算中取瑞利数Ra=107.研究结果表明, 横向黏度变化的最大值出现在上地幔和下地幔中, 达到了2~4个量级, 而中地幔则为1~2个量级[12], 因此在计算中取C1=0.0、1.0、10.0、100.0、500.0和1000.0.
4.1 临界瑞利数Racr临界瑞利数Racr是表征球层中流体由稳定状态(非对流)向非稳定状态(对流)转换的一个物理量.只有当流体的瑞利数大于临界瑞利数时, 对流才可能发生.表 3显示了不同横向黏度变化下不同波长(球谐阶数)的临界瑞利数.表 3表明, 不同横向黏度变化下, 临界瑞利数随波长的变化趋势是相同的:临界瑞利数先随波长增大而减小, 在l=4时达到最小值, 然后增大; 不同波长的临界瑞利数随横向黏度的变化趋势也是相同的:临界瑞利数随横向黏度变化出现减小-增加-减小的趋势, 最小值都出现在C1=1.0处, 最大值都出现C1=10.0处.这表明, 在横向黏度变化小(如C1=1.0)时, 有利于球层中的流体发生热对流运动(与无横向黏度变化C1=0.0时相比); 随横向黏度变化增大, 对应于各波长的临界瑞利数迅速增大, 到C1=10.0时, 临界瑞利数达到最大值, 此时几乎是无横向黏度变化时的临界瑞利数的10倍, 极不利于球层中热对流运动的发生; 随着横向黏度变化的进一步增大, 各波长对应的临界瑞利数虽然有所变化, 但量级与C1=10.0时的相同, 不利于球层中热对流运动的产生.本文结果与随温度变化的黏度模型所获得的结果:各波长的临界瑞利数随黏度差异的增加而逐渐增大[18]有所不同.这表明, 当径向黏度和横向黏度同时随温度变化时, 各波长的临界瑞利数主要受径向黏度变化的控制, 而横向黏度变化则起次要作用.只有在径向黏度结构不变时, 才能凸显横向黏度变化的影响.
|
|
表 3 不同横向黏度变化下各球谐系数的临界瑞利数 Table 3 Critical Rayleigh number corresponding to each spherical harmonic coefficient at different LVV |
平均温度Tm可以表征对流的状态、不同瑞利数下温度扰动的大小和球层中低温、高温区的相对大小, 是一个重要的物理量.定义为[38, 39]

|
(19a) |
其中
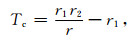
|
(19b) |
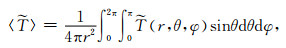
|
(19c) |
图 1显示了不同横向黏度变化下无量纲平均温度Tm和无对流时的温度场Tc随深度的变化曲线.两条曲线之差即为




|
图 1 不同横向黏度变化下无量纲平均温度Tm和无对流时的温度场Tc随深度的变化曲线 Fig. 1 The curves of non-dimensional average temperature Tmand Tc in case of no convection versus depth at different LVV, respectively |
图 2是不同横向黏度变化下对流速度的均方根值随深度的变化曲线.可以看出, 不同横向黏度变化下, 对流速度随深度变化的趋势基本上是一致的, 这表明了横向黏度变化没有改变球层中对流的速度结构.然而, 随着横向黏度变化增强, 对应深度上速度呈现先增大后显著减小的现象(与无横向黏度变化C1=0.0时相比).当横向黏度变化不大于球层中流体的平均黏度η0的一倍时, 对应深度上的速度略微增加, 表明当横向黏度变化不大时, 球层中热对流强度会增强, 起到加速球层中热对流运动的作用; 然后, 随着横向黏度变化进一步增强, 对应深度上的速度显著减小, 特别是C1处于1.0与10.0之间时, 速度减小的梯度较大, 起到阻碍球层中热对流运动的作用; 随后当C1增大到100.0以上时, 尽管对应深度上的速度仍明显小于无横向黏度变化的速度, 但速度差异变化甚微, 这表明横向黏度变化虽然对地幔对流强度有明显的影响, 但是其影响可能仅限制在一定的横向黏度变化强度内.在上地幔, 对流速度随深度几乎呈线性增大, 其斜率随横向黏度变化先减小而后增大; 在下地幔, 速度分布呈马鞍状, 高峰值出现在深度约900 km和2700 km处, 低峰值则出现在中地幔, 深度约1200 km处.Ratcliff等[18]和Stemmer等[19]的研究表明, 随温度变化的黏度结构的球层中, 热对流的均方根速度随深度的变化曲线在上、下边界处的黏度差异小于3个量级时比较相似, 且随黏度差异增大, 对应深度上的速度减小, 而当黏度差异大于3个量级时, 速度分布曲线失去了相似性, 且随黏度差异的增大, 球层浅部的速度减小, 而深部的速度增大, 这表明球层中对流的均方根速度可能主要受径向黏度的控制.

|
图 2 不同横向变化黏度下无量纲速度随深度的变化曲线 Fig. 2 The curves of non-dimensional RMS velocity versus depth at different LVV |
图 3是不同横向黏度变化下环型场速度的均方根值随深度的变化曲线.可以看出, 不同横向黏度下的环型场速度的最大值均出现在上、中地幔, 并且环型场的主要能量也主要集中在上、中地幔, 这不同于总速度场最大值均出现在下地幔的情形.环型场的这种特点可能是其对大地水准面异常和地表地形有明显影响的原因[29, 32].环型场速度并不单一地随着横向黏度变化的增强而增大.当横向黏度变化C1在1.0~10.0之间时, 环型场速度表现出随横向黏度减小的变化, 尔后基本上随着横向黏度变化C1增加而增大, 但在下地幔, 环型场速度增加相对缓慢.随着横向黏度变化增大, 环型场速度占总速度的百分比增大.从约1.0%(C1=1.0)、1.5%(C1=10.0)、7.6%(C1=100.0)、9.6%(C1=500.0)增大到13.8%(C1=1000.0), 这表明即使地幔中存在如此强烈的横向黏度变化, 由此所产生的环型场速度也仅占总速度场的十几个百分点, 这与前人的研究结果基本一致[21].由此说明单纯地利用横向黏度变化所产生环型场的能量很难解释在地表观测到的极型场与环型场能量几乎相等的现象.

|
图 3 不同横向变化黏度下无量纲环型场速度随深度的变化曲线 Fig. 3 The curves of non-dimensional RMS toroidal field velocity versus depth at different LVV |
图 4给出了不同横向黏度变化下的φ=45°的南北向温度扰动剖面.它揭示出在所有的温度剖面中, 在上边界附近存在明显的层状结构; 在下边界附近也存在层状结构, 但是没有上边界层附近的那么显著.在所有剖面中, 正向温度扰动的区域



|
图 4 不同横向变化黏度下φ=45°的温度扰动图像(图中数字单位为无量纲) (a)C1=0.0;(b)C1=1.0;(c)C1=10.0;(d)C1=100.0;(e)C1=500.0;(f)C1=1000.0. Fig. 4 The profiles of fluctuating temperature at φ=45° for different LVV |
图 5是对应于图 4的对流剖面.图 5揭示出, 所有剖面中均存在4个对流胞, 靠近赤道的两个对流胞的横纵比(约为2.2)比靠近两极的对流胞的横纵比(约为1.76)略大; 在对流胞的顶部, 形成了一个几乎静止的盖层, 与其下面强烈的对流运动形成了强烈的反差.各对流剖面中的对流速度大小有差异.随横向黏度变化增强, 对流速度先增大(图 5b), 然后逐渐减小, 最后达到速度变化微弱的状态, 即相对稳定的状态(图 5(d~f)).表明横向黏度的变化没有改变球层中热对流的对流结构, 仅可能对对流结构起到一定的调节作用.这与实验结果[42]和数值模拟结果[43, 44]一致.

|
图 5 不同横向变化黏度下φ=45°的对流图像 (a)C1=0.0;(b)C1=1.0;(c)C1=10.0;(d)C1=100.0;(e)C1=500.0;(f)C1=1000.0. Fig. 5 The convection patterns at φ=45° for different LVV |
前人在研究横向黏度变化的影响时, 常常采用温度依赖的黏度结构[14~19].这种黏度结构同时包含了径向黏度和横向黏度.径向黏度可能对地幔对流起控制作用, 而横向黏度则起次要的调节作用[29, 31, 32], 这就使得难以真正认识横向黏度变化对对流的影响.本文在径向黏度为常数的基础上, 加上了一个仅随余纬度变化的横向黏度变化项
横向黏度变化可以加速或阻碍球层中的热对流.当横向黏度变化不大(如C1=1.0)时, 球层中热对流的临界瑞利数减小, 均方根速度增大, 横向黏度变化起到了加速热对流的作用; 随着横向黏度变化增强, 临界瑞利数剧增, 均方根速度显著减小, 横向黏度变化起到阻碍球层热对流的作用.
横向黏度变化对球层中热传输方式有调节作用.当横向黏度变化不大(如C1=1.0)时, 对应深度上的横向平均温度曲线几乎与无横向黏度变化时的重合, 表明小横向黏度变化对球层中热对流的热传输方式几乎没有影响.随着黏度变化增强, 球层中的低温区逐渐扩张, 高温区逐渐收缩, 表明热传导传热增强, 对流传热减弱.横向黏度变化增强到一定程度时, 这两种方式的作用会达到相对平衡.不过, 无法改变球层中高温区占优势的状况, 表明横向黏度变化仅对球层中热传输方式有一定的调节作用.
横向黏度变化对球层中热对流影响限制在一定的范围内.当横向黏度变化大于100倍时, 球层中热对流的临界瑞利数、横向平均温度、均方根速度以及温度扰动场随横向黏度变化很小, 达到了一个相对的稳定状态; 而它们在横向黏度变化处于1~100倍之间时, 变化的梯度较大, 即横向黏度变化对它们的影响较明显.
横向黏度变化所产生的环型场能量主要集中在中、上地幔.环型场速度占总速度场的比例随着横向黏度变化而增大, 但最多仅占总速度场的十几个百分点, 因此仅利用横向黏度变化所产生的环型场能量难以解释观测到的地表板块运动中的环型场能量大小.
附录A:

|
(A1) |
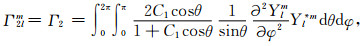
|
(A2) |

|
(A3) |

|
(A4) |

|
(A5) |

|
(A6) |

|
(A7) |

|
(A8) |

|
(A9) |

|
(A10) |

|
(A11) |

|
(A12) |

|
(A13) |

|
(A14) |

|
(A15) |

|
(A16) |

|
(A17) |

|
(A18) |

|
(A19) |

|
(A20) |

|
(A21) |

|
(A22) |

|
(A23) |

|
(A24) |

|
(A25) |

|
(A26) |

|
(A27) |

|
(A28) |

|
(A29) |

|
(A30) |

|
(A31) |

|
(A32) |

|
(A33) |
| [1] | Elsasser W M. Sea floor spreading as thermal convection. J.Geophys.Res , 1971, 76: 1101-1112. DOI:10.1029/JB076i005p01101 |
| [2] | Christensen U. Convection with pressure-and temperaturedependent non-Newtonian rheology. Geophys.J.R.Astron.Soc , 1984, 77: 343-384. DOI:10.1111/j.1365-246X.1984.tb01939.x |
| [3] | Moresi L N, Solomatov V S. Numerical investigation of 2D convection with extremely large viscosity variation. Phys.Fluids , 1995, 7: 2154-2164. DOI:10.1063/1.868465 |
| [4] | Bercovici D, Schubert G, Glatzmaier G A. Three-dimentional spherical models of convection in the Earth's mantle. Science , 1989, 244: 950-955. DOI:10.1126/science.244.4907.950 |
| [5] | Bercovici D, Schubert G, Zebib A. Geoid and topography for infinite Prandtl number convection in a spherical shell. J.G.R. , 1988, 93(B6): 6430-6436. DOI:10.1029/JB093iB06p06430 |
| [6] | 叶正仁, 滕春凯, 张新武. 地幔对流与岩石圈板块的相互耦合及影响--(Ⅰ)球腔中的自由热对流. 地球物理学报 , 1995, 38(2): 174–180. Ye Z R, Teng C K, Zhang X W. Coupling between mantle circulation and lithospheric Plates-(Ⅰ) Thermal free convection in a spherical shell. Acts Geophysica Sinica (in Chinese) , 1995, 38(2): 174-180. |
| [7] | 傅容珊, 王毅, 黄建华, 等. 黏滞分层地幔中密度异常驱动对流模型的研究. 地球物理学报 , 2005, 48(4): 824–833. Fu R S, Wang Y, Huang J H, et al. Effect of rheology structure on flow patterns driven by density anomaly in the mantle. Chinese J.Geophys (in Chinese) , 2005, 48(4): 824-833. |
| [8] | Weertman J. The creep strength of the Earth's mantle. Rev.Geophys , 1970, 8: 145-168. DOI:10.1029/RG008i001p00145 |
| [9] | Karato S I, Wu P. Rheology of the upper mantle:a synthesis. Science , 1993, 260: 771-778. DOI:10.1126/science.260.5109.771 |
| [10] | Hager B H. Subducted slabs and the geoid:constrains on mantle rheology and flow. J.Geophys.Res , 1984, 89: 6003-6015. DOI:10.1029/JB089iB07p06003 |
| [11] | Mitrovica J X, Peltier W R. Constrains on mantle viscosity based upon the inversion of post-glacial uplift data from the Hudson Bay region. Geophys.J.Int , 1995, 122: 353-370. DOI:10.1111/gji.1995.122.issue-2 |
| [12] | Ranalli G. Mantle rheology:radial and lateral viscosity variations inferred from microphysical creep laws. Journal of Geodynamics , 2001, 32(4-5): 425-444. DOI:10.1016/S0264-3707(01)00042-4 |
| [13] | Christensen U, Harder H. 3D convection with variable viscosity. Geophys.J.Int , 1991, 104: 213-226. DOI:10.1111/gji.1991.104.issue-1 |
| [14] | Sunder-Plaβmann T, Christensen U. A test of approximations for modeling convection with temperaturedependent viscosity. Physics of the Earth and Planetary Interiors , 2000, 120: 103-110. DOI:10.1016/S0031-9201(00)00147-3 |
| [15] | Zhong S, Zuber M T, Moresi L, Gurnis M. Role of temperature-dependent viscosity and surface plates in spherical shell models of mantle convection. J.Geophys.Res , 2000, 105(B5): 11063-11082. DOI:10.1029/2000JB900003 |
| [16] | Tackley P. Effects of strongly temperature-dependent viscosity on time-dependent, three-dimensional models of mantle convection. Geophys.Res.Lett , 1993, 20: 2187-2190. DOI:10.1029/93GL02317 |
| [17] | Tackley P. Effects of strongly variable viscosity on threedimensional compressible convection in planetary mantles. J.Geophys.Res , 1996, 101: 3311-3332. DOI:10.1029/95JB03211 |
| [18] | Ratcliff J T, Schubert G, Zebib A. Steady tetrahedral and cubic patterns of spherical shell convection with temperaturedependent viscosity. J.Geophys.Res , 1996, 101(B11): 25473-25484. DOI:10.1029/96JB02097 |
| [19] | Stemmer K, Harder H, Hansen U. A new method to simulate convection with strongly temperature-and pressuredependent viscosity in a spherical shell:Applications to the earth's mantle. Physics of the Earth and Planetary Interiors , 2006, 157: 223-249. DOI:10.1016/j.pepi.2006.04.007 |
| [20] | Yoshida M, Nakakuki T. Effects on the long-wavelength geoid anomaly of lateral viscosity variations caused by stiff subducting slabs, weak plate margins and lower mantle rheology. Physics of the Earth and Planetary Interiors , 2009, 172: 278-288. DOI:10.1016/j.pepi.2008.10.018 |
| [21] | Cadek O, Fleitout L. Effect of lateral viscosity variations in the coremantle boundary region on predictions of the long wavelength geoid. Stud.Geophys.Geod , 2006, 50: 217-232. DOI:10.1007/s11200-006-0013-0 |
| [22] | Wang H, Wu P. Effects of lateral variations in lithospheric thickness and mantle viscosity on glacially induced relative sea levels and long wavelength gravity field in a spherical, selfgravitating Maxwell Earth. Earth and Planetary Science Letters , 2006, 249: 368-383. DOI:10.1016/j.epsl.2006.07.011 |
| [23] | Oliver D S, Booker J R. Planform of convection with strongly temperature-dependent viscosity. Geophysical & Astrophysical Fluid Dynamics , 1983, 27(1): 73-85. |
| [24] | 朱涛, 冯锐. 球层中的非线性自由热对流--变黏度模型. 地震学报 , 2005, 27(2): 194–204. Zhu T, Feng R. Nonlinear free thermal convection in a spherical shell:A variable viscosity model. Acta Seismologica Sinica (in Chinese) , 2005, 27(2): 194-204. |
| [25] | Balachandar S, Yuen D A, Reuteler D M. Localization of toroidal motion and shear heating in 3-D high Rayleigh number convection with temperature-dependent viscosity. Geophysical Research Letters , 1995, 22(4): 477-480. DOI:10.1029/94GL03046 |
| [26] | Zhang S, Yuen D A. Intense local toroidal motion generated by variable viscosity compressible convection in 3D spherical shell. Geophysical Research Letters , 1996, 23(22): 3135-3138. DOI:10.1029/96GL03029 |
| [27] | 叶正仁, 王建. 上地幔变黏度小尺度对流的数值模拟. 地球物理学报 , 2003, 46(3): 335–339. Ye Z R, Wang J. A numerical research on the small-scale convection with variable viscosity in the upper mantle. Chinese J.Geophys (in Chinese) , 2003, 46(3): 335-339. |
| [28] | Koch D M, Ribe N M. The effect of lateral viscosity variations on surface observables. Geophys.Res.Lett , 1989, 16: 535-538. DOI:10.1029/GL016i006p00535 |
| [29] | Richards M A, Hager B H. Effects of lateral viscosity variations on long-wavelength geoid anomalies and topography. J.Geophys.Res , 1989, 94: 10299-10313. DOI:10.1029/JB094iB08p10299 |
| [30] | Ribe N M. The dynamics of thin shells with variable viscosity and the origin of toroidal flow in the mantle. Geophys.J.Int , 1992, 110: 537-552. DOI:10.1111/gji.1992.110.issue-3 |
| [31] | Cadek O, Richard Y, Martinec Z, et al. Comparison between Newtonian and non-Newtonian flow driven by internal loads. Geophys.J.Int , 1993, 112: 103-114. DOI:10.1111/gji.1993.112.issue-1 |
| [32] | Zhang S, Christensen O. Some effects of lateral viscosity variations on geoid and surface velocities induced by density anomalies in the mantle. Geophys.J.Int , 1993, 114: 531-547. DOI:10.1111/gji.1993.114.issue-3 |
| [33] | Ogawa M, Schubert G, Zebib A. Numerical simulations of three-dimensional thermal convection in a fluid with strongly temperature-dependent viscosity. J.Fluid Mech , 1991, 233: 299-328. DOI:10.1017/S0022112091000496 |
| [34] | Zebib A. Linear and weakly nonlinear variable viscosity convection in spherical shells. Theor.Comput.Fluid Dyn , 1993, 4: 241-253. DOI:10.1007/BF00417930 |
| [35] | Ratcliff J T, Schubert G, Zebib A. Three-dimensional variable viscosity convection of an infinite Prandtl number Boussinesq fluid in a spherical shell. Geophys.Res.Lett , 1995, 22: 2227-2230. DOI:10.1029/95GL00784 |
| [36] | 傅容珊, 黄建华. 地球动力学. 北京: 高等教育出版社, 2006 . Fu R S, Huang J H. Geodynamies (in Chinese). Beijing: China Higher Education Press, 2006 . |
| [37] | Buckus G. A class of self-sustaining dissipative spherical dynamos. Ann.Phys , 1958, 4: 381-384. |
| [38] | Zebib A, Schubert G, Straus J M. Infinite Prandtl number thermal convection in a spherical shell. J.Fluid Mech , 1980, 97(2): 257-277. DOI:10.1017/S0022112080002558 |
| [39] | 叶正仁, 滕春凯, 张新武. 地幔对流与岩石圈板块的相互耦合及影响---(I)球腔中的自由热对流. 地球物理学报 , 1995, 38(2): 174–180. Ye Z R, Teng C K, Zhang X W. Coupling between mantle circulation and lithospheric Plates-(I) Thermal free convection in a spherical shell. Chinese J.Geophys.(Acta Geophysica Sinica) (in Chinese) , 1995, 38(2): 174-180. |
| [40] | 朱涛, 冯锐. 球层中高阶自由热对流格局及其变化的研究. 地震学报 , 2005, 27(1): 11–24. Zhu T, Feng R. The patterns of high-degree thermal free convection and its features in a spherical shell. Acta Geophysica Sinica (in Chinese) , 2005, 27(1): 11-24. |
| [41] | 杨柳, 陈艳萍. 求解非线性方程组的一种新的全局收敛的Levenberg-Marquardt算法 , 2008, 30(4): 388–396. Yang L, Chen Y P. A new globally convergent LevenbergMarquardt method for solving nonlinear system of equations. Mathematica Numerica Sinica (in Chinese) , 2008, 30(4): 388-396. |
| [42] | Davaille A. Transient high-Rayleigh number thermal convection with large viscosity variations. J.Fluid Mech , 1993, 253: 141-166. DOI:10.1017/S0022112093001740 |
| [43] | Solomatov V S. Scaling of temperature-and stress-dependent viscosity convection. Phys.Fluids , 1995, 7: 266-274. DOI:10.1063/1.868624 |
| [44] | Dumoulin C, Doin M P. Heat transport in stagnant lid convection with temperature-and pressure-dependent Newtonian or non-Newtonian rheology. J.Geophys.Res. , 1999, 104: 12759-12778. DOI:10.1029/1999JB900110 |
 2010, Vol. 53
2010, Vol. 53