2. 中国科学院研究生院, 北京 100049
2. Graduate University of Chinese Academy of Sciences, Beijing 100049, China
1976年MS7.8唐山大地震是20世纪发生在我国华北地区的灾难性事件.由于地震发生在人口密集的唐山市,造成了巨大的生命和财产损失.近三十多年来,国内外科学家对该发震断层的力学机制,区域应力场特征,地震波传播和地震危险性分析以及唐山主震对余震的触发从地质和地球物理等不同角度进行了广泛的研究[1~5],也为未来华北地区潜在地震危险性预测提供了宝贵的资料.
由于缺乏该地震的近场地震动记录,所以如何利用理论和数值计算方法研究断层的破裂过程,合理估算唐山主震的地震动特点,以用来了解地震的破裂机制,解释震害分布,总结工程抗震的经验,成为一项非常具有理论价值和实际意义的研究课题.目前,用于研究断层破裂过程及其强地面运动的方法主要是有限断层运动学方法和动力学方法.运动学震源模型是已知断层形状、大小、位置等几何参数,以及断层面上滑移和滑移速率的时空分布、破裂速度和破裂传播方式等,并已知断层周围的介质构造和参数,求解地震动场.动力学震源模型的不同之处在于其已知条件不是断层面上错动的分布,而是初始应力场和断层面岩石的破裂强度,按照一定的破裂准则求解断层面的破裂过程(即位错的时空分布、破裂的传播过程)和地震动场[6],动力学模型比运动学模型更能深刻地揭示断层破裂的力学本质.随着高速计算机的普遍,特别是三维数值模拟技术也逐步趋于成熟,基于震源动力学过程模拟地震波传播和强地表运动的研究已成为现代地震灾害和危险性分析的一个重要组成部分,它使得我们能够在对震源过程认知的基础上,采用合理的数值模拟技术,较为真实地模拟断层动态破裂过程,地震波传播和与之对应的近场地表运动,以弥补现今强震观测数据的不足.数值求解断层动态破裂过程通常采用有限差分[7~10],有限元方法[11]以及边界元方法[12, 13].本文采用美国南加州地震委员会(SCEC)Steven Day博士所发展的3D-FDM断层动态破裂模型,对1976年MS7.8唐山地震断层破裂和近断层地表运动进行模拟.该模型有其自身的优势所在:(1)Day [14]从发展该模型至今已有二十多年了,断层破裂和传播过程的许多新成果和认识都在模型中得到了应用.(2)模型被广泛应用于南加州地区的地表运动预测[15, 16].(3)Day [17]将该模型定量与物理实验结果对比,研究结果十分相近.(4)该模型是用于求解断层剪切破裂模式的模型,那么针对于唐山地震,由于其是高角度的右旋走滑错动,倾角80°[18, 19],因此可以对唐山地震做出较为合理的近似,将唐山地震的发震断层理想化为垂直走滑断层以对其震源的破裂过程及近断层强地面运动进行模拟.
对于唐山地震的震源动力学及近断层地震动,前人也做了一定的研究.北京大学的蔡永恩(1999)等[20]用新LDDA(Lagrangian Discontinuous Deformation Analysis)方法模拟了唐山地震断层的破裂、错动和应力释放的整个动力过程.谢礼立等[21](1994)建立了非均匀的唐山主震断层模型,利用广义反射-透射系数矩阵和离散波数方法,考虑局部场地效应,给出了唐山及周边地区地震动的时间过程的数值模拟结果.本文在Day博士的三维有限差分程序基础之上进行改进,在小型的DELL工作站上实现了并行计算,从简化的双侧断层破裂模式出发,对该唐山地震发震断层的动态破裂过程及近断层地表运动特征进行了仿真模拟和计算.在此研究的基础上,也为华北地区逐步实现地震断层破裂预测模型(Earthquake Fault Rupture Forecasting Model,EFRFM)做好前期准备.地震断层破裂预测模型的建立可为我们今后潜在地震危险性评估提供更为完整的数据体.
2 震源动态破裂过程与模型建立原则 2.1 模型的初始条件和结构性质本文在进行模拟计算时,断层的破裂源自剪切应力松弛,在断层面上发生一系列的剪切破裂.在此动态破裂的模型中,需要首先设定介质的初始应力状态,断层的破裂速度,破裂面的有限边界,以及破裂后断层滑动过程中所遵循的破裂准则.模型中,虽然破裂前缘的速度是被设定好的,但是在断面上特定点的滑移上升时间是未知的.滑动终止是非线性摩擦定律作用的结果,即滑移弱化摩擦定律.在该模型中,Day [14]指出当破裂时间小于0时,介质处于应力平衡状态且各处的速度均为0,此时层面受到均匀的剪切牵引力τ0和正压牵引力σn作用,没有考虑垂向应力的作用.模拟计算的介质被视为假性的黏弹性性介质,即为了能够使地震波在传播过程中逐渐衰减,人为的加了一个阻尼,即为下文所提到的黏弹性系数.
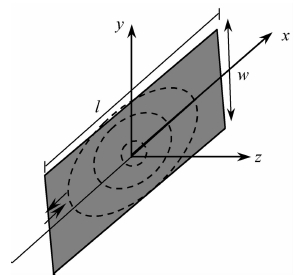
2.2 断层动态破裂的扩展模式在本文的模拟中,断层的破裂面为一个带有单位矢量的预设面[14],模型假定断层面破裂的延展取决于震源时间函数,破裂初始于一点并且按照一定的破裂速度VR对称地向外扩展延伸,终止于预设的矩形边界(如图 1).
|
图 1 断层破裂面示意图 Fig. 1 A sketch map of fault rupture plane |
Σ(t)表示断层面的一部分,断层面破裂到t时刻,w和l分别表示矩形断层的宽度和长度,x和y表示笛卡尔坐标系下的x轴和y轴,其中Σ(t)包含的所有的点x,y满足下式:
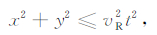
|
(1) |
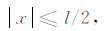
|
(2) |
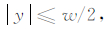
|
(3) |
该破裂模型在一定程度上要基于两个人为的假设,其一,在破裂的初始时刻,破裂速度从0瞬时增加到破裂的最终速度;其二,在破裂停止的时刻,破裂速度在断层的边界瞬时减为0.前者的假设有一个较好的物理基础,理论的[22, 23]和实验室[24]证据均可表明破裂的速度能够快速增加到其破裂的最终的速度.而对于后者断层突然停止时,对破裂速度的假设比较难找到实验室证据的支持,因为目前在实验室所进行的岩石力学的试验均是完全破裂的.但是对于突然停止的假设也并非是完全人为的假设,Husseini et al.[25]已经表明当断层突然遇到一个障碍体时破裂是能够突然停止的,破裂的边界不存在惯性,这一点至少是适合线弹性介质的.采用这种破裂停止模式可以辐射高频的地震波,Madariaga[26]指出最强的高频波的产生与破裂速度的突然变化有密切关系.
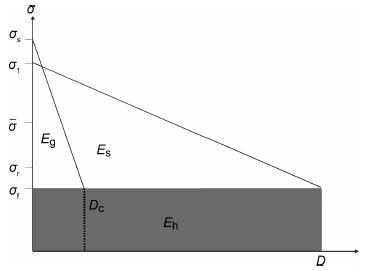
2.3 断层破裂的边界条件和摩擦定律当断层破裂后,产生了两个新的破裂面,在很高的围压下,两个新的断层面之间开始相对摩擦滑动,这是一个典型的动力接触问题,需要建立合理的模型来描述断层两盘之间的相互作用力,内聚区(Cohesivezone)摩擦模型就是因此而引入的.这里支持断层破裂原则的一个基本的假设是:材料的强度是有限的,以便在破裂边缘发生应力集中时不会超过预先所设定的屈服应力.实际的断层破裂过程中在已破裂和未破裂之间有一部分区域处于部分破裂状态,这一部分区域被称为内聚区[6].Ida[27]发展了一种内聚力模型,在这个模型中,内聚区域的应力与破裂面之间的滑动距离有关,这个模型后来被称为滑动弱化模型(图 2).Andrews[28]利用这个模型和Griffith破准则研究了平面内剪切破裂(双侧破裂)在均匀弹性全空间中破裂过程.滑动弱化模型有很好的物理基础,Dieterich[29]的岩石破裂实验结果表明,当断层上一点的剪切应力超过其应力强度时,该点开始破裂并滑动,随着位错的增加,剪切应力以某种方式下降,当位错距离达到一定值Dc(Dc被称为滑动弱化距离,也称为临界滑动位移),剪应力下降到一个稳定的值,这个值一般指断层两盘之间的动摩擦应力.滑移弱化摩擦准则决定了断层破裂的边界条件.在本文模型的断层面上,滑移区正应力连续,法向位移连续,断面两侧位移不连续,粘着区正应力连续,沿断层方向和断层法向上的位移也连续,局部剪应力小于最大静摩擦应力.
|
图 2 滑移弱化摩擦模型示意图 Es,Eg和Eh分别为破裂能,地震波辐射能以及断层摩擦所产生的热能;Dc为临界滑动位移.σ1和σf分别为断层上的初始应力和最终应力.σs和σr分别为断层破裂前缘的屈服应力和断层滑动时的平均摩擦应力. Fig. 2 A sketch map of the slip-weakening model in which Es, Eg and Eh belong to fracture energy, radiated seismic energy and heat energy caused by fault frictional motion, respectively. Dc is the critical slip length involved in the slip weakening model.σl and σf are the initial and final stresses on the fault, respectively. σs and σr are the yield and averaged frictional stresses, respectively |
数值模拟所采用的理论方法是模拟计算是否合理有效的基础.根据上述理论,Day[30]设定埋藏于半无限空间中断层Σ两侧出现位移不连续,那么根据线弹性动力学,描述半无限空间质点运动的方程可写为
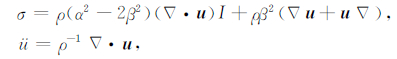
|
(4) |
其中,σ为应力张量,u是质点位移向量,α和β分别是P波和S波的速度,ρ为介质密度,I为单位张量.设垂直于断层Σ的单位向量为n,那么断层两侧的位移间断可表示为
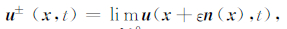
|
(5) |
平行于断层的剪切位移量可由下式求得:
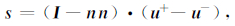
|
(6) |
滑移速率由ṡ表示.
假定穿过断面Σ的正向牵引力σ·n连续,而剪切牵引力可表示为(I-nn)σ·n,其值大小由τ表示.如果断层摩擦强度τc给定,根据回跳条件,有
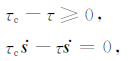
|
(7) |
如果断层摩擦强度同断层正向应力有关,即

|
(8) |
其中,σn为作用于断层面的正向应力,μf为摩擦系数,l为滑移变量.根据滑移弱化准则μf可写为
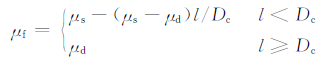
|
(9) |
其中,μs和μd分别为静摩擦系数和动摩擦系数;Dc为临界滑移距离[27, 28].在整个断面上,正应力和摩擦系数是常量.由回跳条件方程(7)和摩擦定律方程(9),以及断面上合适的初始应力条件构成了断层的破裂模型,为了追踪每一点的破裂状态一些无记忆的变量事先不得不被指定.当方程(7)中的摩擦力等于剪切应力时破裂开始发生,此时属于能量积累的过程.破裂后,能量释放,断层面相对着的两侧各自回跳到其平衡位置.基于上述理论,利用有限差分的方法实现了对断层的自发破裂的模拟过程.
3 唐山主震的震源及计算模型参数约束条件由上述的动力学模型建立原则可知,模拟唐山地震震源破裂过程及近断层地震动特征需要基于一定前提条件,其包括震源位置,断层尺度,平均应力降及地震波传播介质模型.唐山地震后,国内外研究学者利用地形变、体波及面波资料等对震源机制和震源参数做了分析反演,积累了一定量的反演数据[31~35].通过对比和总结可以得到唐山地震断层破裂的特征较为一致的定性结果,主要表现为:
(1)唐山7.8级主震的发震断层为NE向唐山断裂,表现为高倾角的右旋走滑错动性质,走向与华北地区构造应力场主压应力方向大致相同,北偏东,方位角介于30°~50°之间.
(2)唐山地震为双侧破裂地震,沿北东南西向两侧扩展,触发位置位于断层的中间部位,且断层在震中附近位错较大.
(3)震中附近及西南段的断层破裂所辐射的能量占能量的大部分,断层的东北端辐射能量较少.这一点可以从唐山地震的烈度分布图得到很好体现.根据国家地震局地震研究所1985年编制的唐山地震震害分布图中显示房屋的倒塌率在90%~95%的区域主要集中在唐山断裂的西南段,说明此处的烈度最大,对应地表运动的速度和加速度也较大.
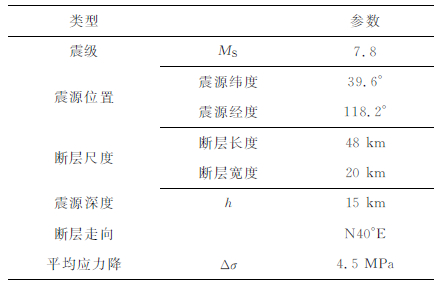
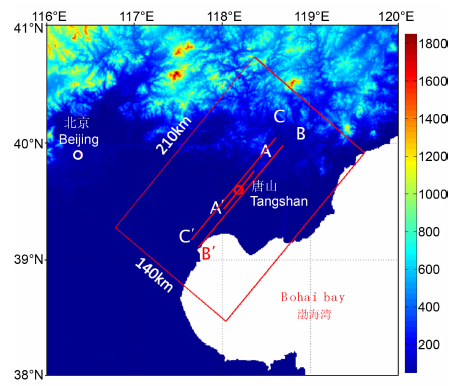
通过对唐山地震断层破裂特征的分析研究以及对现有的基本的震源参数的对比分析,我们采用了Huang和Yeh[35]由同震地壳变形反演得到的结果,所选取断层长度和宽度分别为48km和20km,震源深度为15km,震中位于断层的中间,为一双侧破裂.在目前的研究工作中,我们选定研究区域为围绕断层210km×140km×40km的长方形块体.计算区域的地表投影见图 3.具体震源模型参数见表 1.
|
图 3 数值模拟地表区域(长为210km,宽为140km),其中红色圆圈为震中,AA′为断层在地表的投影,BB′和CC′分别为平行于断层走向距断层5km处的观测线 Fig. 3 On the map, the simulation region is covered by a rectangle (210 km long along the fault-parallel direction and 140 km wide along the fault-normal direction). The faut trace on the surface is indicated by AA', and the earthquake hypocenter s shown by a solid red circle. The lines of BB' and CC' are the oft-fautt (5 km) receiver locations for the 3D-FDM model, which are parallel with the fautt strike-direction |
|
|
表 1 震源模型参数 Table 1 Source parameters of the model |
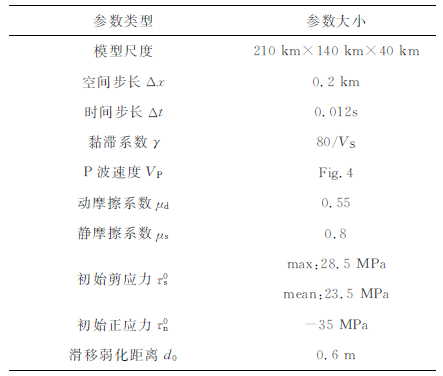
断层的三维自破裂的模拟对计算机性能的要求相当高,本文在模拟计算时所采用的是小型的Dell工作站,内存为16GB.模拟计算所采用的空间分辨率和时间分辨率分别为200m和0.012s,x,y,z三个方向的计算节点分别为1051,201和701,计算的节点数达1.48×108个,计算长度为4000个时间步长,完成一次模拟需要的时间约为54h.这一分辨率能够较好地模拟计算出地震发生时所产生的低频波部分(≤1 Hz).由于计算的节点数很高,需要通过并行处理来完成模拟计算,计算中将整个区域共划分为10个进程,其中x方向上5个进程,y方向2个进程,z方向1个进行,从而保证了模拟计算的顺利进展.具体的计算模型参数见表 2.
|
|
表 2 计算模型参数 Table 2 Modeling Parameters |
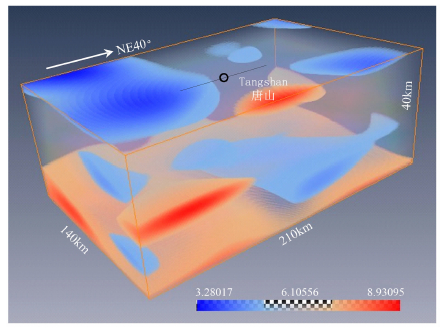
在模拟计算中我们对震源参数做了一个比较理想的近似,把唐山的发震断层作为一个垂直的右旋走滑正断层来处理,断面的初始应力为均匀分布,触发震源破裂的初始应力见表 2.本文研究区域的3D地壳速度结构使用于湘伟和陈运泰[36]根据地震层析成像反演得到的结果,并对其进行三维插值所得.该区域的P波速度分布特征如图 4.对速度结构的三维可视化体现了计算区域中的速度结构的横向不均匀性,其中蓝色为低速区,红色为高速区,由图 4可见唐山发震断层西南区域存在一较为明显的低速带.
|
图 4 唐山地区三维P波三维速度结构(单位:km/s) 图中绘制有效地可视化了唐山地区三维速度结构,该区域的长度,宽度和厚度分别为210km,140km和40km,其中深度方向上按照比例放大了2倍.圆圈代表唐山地震震中位置,黑色实线为发震断层地表投影. Fig. 4 A 3D velocity structure (P-wave) of Tangshan area (unit: km/s) Volume rendering is very intuitive to visualize the velocity structure of the whole simulation region (210 km × 140 km × 40 km), The vertical axis (depth direction) has been rescaled twice. The circle and solid line show the earthquake epicenter and fault trace, respectively. |
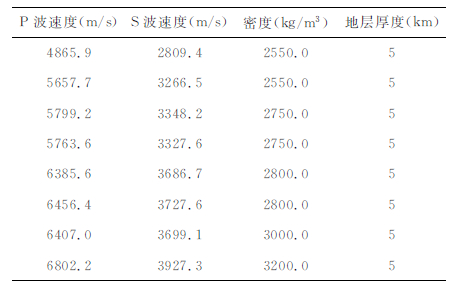
为了能够更进一步说明3D速度结构的横向不均性对地表运动带来的影响,这里我们也取了1D速度结构对整个区域进行了模拟计算,数据同样是源自于湘伟和陈运泰[36],我们将其原始数据在每一层做了一个平均,得到的速度结构在垂向上是变化的,但是在横向上是均匀的.模拟结果的对比分析将在下文详细阐述.具体参数如表 3.
|
|
表 3 唐山地区一维地壳结构 Table 3 1D crustal structure in Tangshan area |
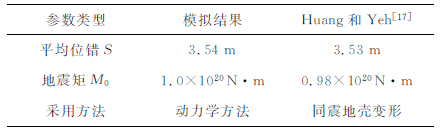
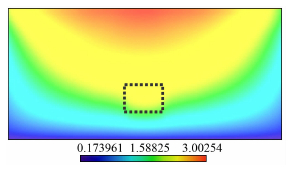
由Huang和Yeh[35]根据同震形变反演的断层尺度和静态应力降作为约束,以及利用表 1和表 2中所列参数,得到震后断面位移分布如图 5所示,计算所得的平均位错和地震矩与Huang和Yeh[35]非常相似,如表 4.地震矩约束为本文地表运动模拟的可靠性提供了一个有力的依据.
|
图 5 断面最终滑动位移分布特征(单位:m) 虚线长方型区域为破裂起始区,滑动位移在地表附近达到最大值,平均位错和宏观地震矩与同震形变分析结果(Huang和Yeh[35])一致. Fig. 5 The distribution of final slip on the fautt (in units of m). The dashed rectangle indicates the rupture initiating area which is usually called earthquake epicenter. The maximum slip occurs near free surface and the average slip displacement and seismic moment are similar to the results from Huang and Yeh[35] derived from coseismic crustal deformation observation. |
|
|
表 4 模拟计算得到的地震矩和平均位错与Huang和Yeh[17]结果对比 Table 4 A comparison of modeled seismic moment and averaged slip-displacement with Huang和Ye[17] |
通过三维断层瞬态破裂模拟,我们对唐山地震的破裂过程和由此造成的近断层地表运动有了一个更为清晰的认识.根据模拟计算结果的分析,我们着重讨论了区域速度结构和有限断层破裂方向性对地表运动的影响.根据初步研究结果以及结合京津唐地区活动断层构造特征,我们对唐山Ms7.8级主震后随之而来的1976滦县Ms7.1级余震及宁河Ms6.9级余震的触发机制提出了新的解释.
4.1 速度结构对地表运动的影响首先,我们讨论地壳速度结构对地表运动的影响.为了能够更好地得出三维速度结构的横向不均性对地表运动的影响,本文分别根据三维地壳速度结构和一维地壳速度结构对唐山地震进行了数值模拟,并且分别给出了由两者模拟计算得到的地表峰值加速度和时程曲线.
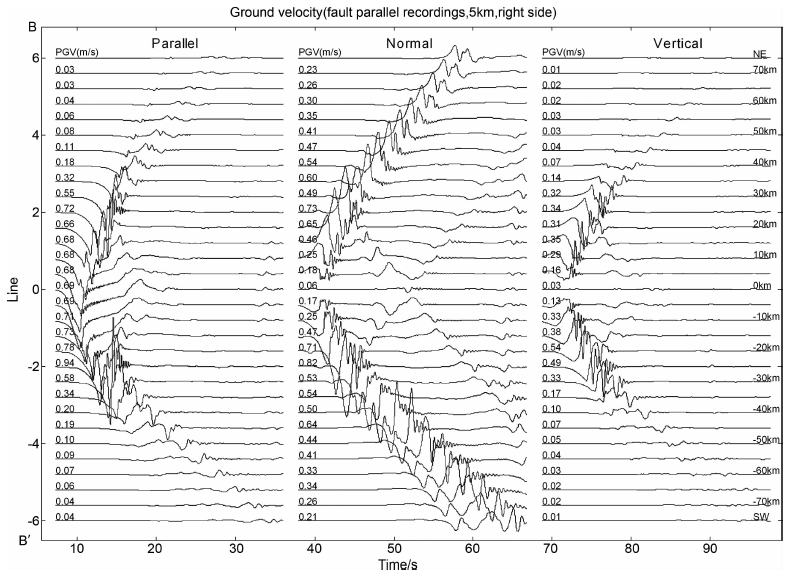
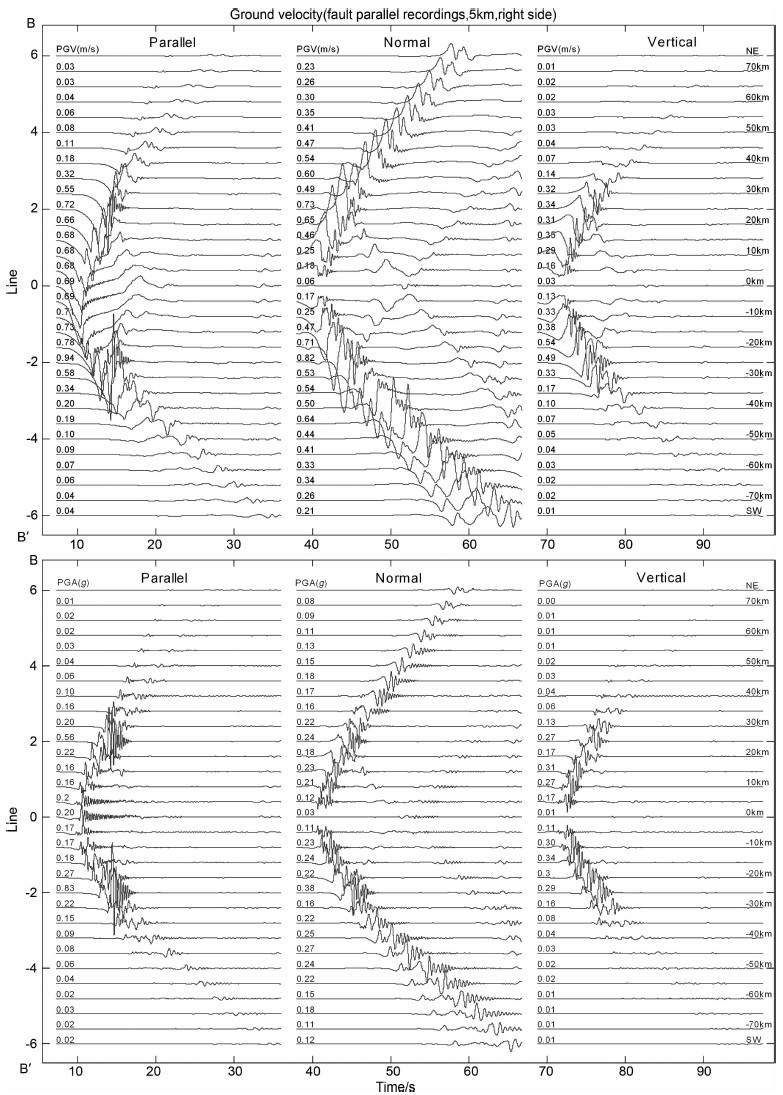
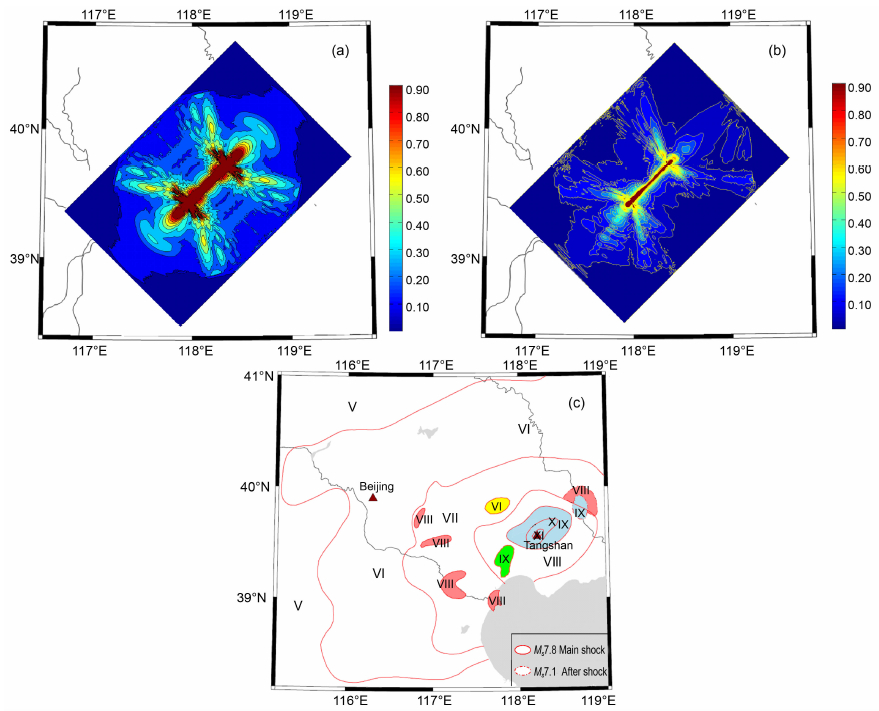
图 3中BB′和CC′是位于断层两侧且平行于断层(距断层5km处)的观测线,测线全长为150km,从中点向东北方向和西南方向各自延伸75km.从一维速度结构得到时程曲线(图 6)和地表峰值加速度(图 8a)可以看出,得到的地表峰值加速度是完全对称的.因为本文模拟计算时断面的初始应力分布是均匀的,如果速度结构在横向上也是均匀的话,则得到的地表峰值速度和加速度势必也是对称的,那么这样和实际情况明显也是不符合的.所以本文的一个很重要的结果就是模拟计算中嵌入了三维速度结构,一方面加强了模拟计算的真实性,同时也有利于减少速度结构的横向不均性对地表运动产生的影响.地壳三维速度结构的横向不均匀使得地震波的传播也出现了横向的不均匀.嵌入三维速度结构之后模拟计算得到地表峰值加速度和唐山地震造成的地表震害分布有一个较好的对应关系.图 7A和7B分别给出了BB′和CC′两条测线(距断层5km)的速度和加速度的时程曲线.其中横坐标是地震波的传播时间,纵坐标是测点.在目前的模型中唐山地震断层破裂为一双向破裂过程,地震波辐射和传播分别沿测线中点向西南和东北两个方向传播.图中的三个纵列分别代表水平方向上与断层平行和垂直的两个质点运动分量和垂直于地表方向的质点运动分量的时程曲线.从图中可以看出断层向两边的传播速度是不同的,沿西南方向传播的快,且速度和加速度也较大.观察图 7A,断层右侧5km的测线的地表运动速度和加速度时程曲线,离该剖线中点位置都为45km,但传播方向分别为西南向和东北向的两点的速度和加速度峰值分别为0.64m/s,0.27g和0.47m/s,0.18g.从唐山地震近场地表水平峰值加速度分布特征图 8b也可以看出在整个计算区域中,唐山断裂带西南区域地表运动的水平峰值加速度要强于东北部的加速度,这与唐山地震的烈度分布特征也是相对应的(图 8c),谢礼立等[21]也提到唐山断层西南端辐射的能量较大,东北段辐射能较小.根据本文模拟计算我们对这一现象的一个初步的解释是,唐山断裂西南区域的低速带导致了更强的地表运动的产生.另外,图 8b中模拟得到的峰值加速度(PGA)还显示断层附近和端点的加速度较大,近断层均可以达到0.9g以上.而随着离开断层的距离加大,加速度也快速衰减.随着离开断层距离的增加,速度结构引起地表运动差异也越来越明显,并且断层两侧的衰减也是不对称的,右侧(断层东南侧)衰减较慢,左侧(断层西北侧)衰减较快.而通过一维速度结构模拟计算得到的地表的PGA的衰减速度是一致的(图 8a),且整体衰减较慢.
|
图 6 沿断层走向位于断层右侧(BB′)5km处地表质点速度时程曲线,每一道上的数字表明的是该点峰值速度(1D速度结构) Fig. 6 Time histories of particle velocities observed on BB' line which is located on the right side of the fault with an off-set of 5 km away from fault trace (1Dvelocity model). The peak values of particle velocities and accelerations are shown on the left side of each trace |
|
图 7A 沿断层走向位于断层右侧(BB′)5km处地表质点速度时程曲线(上);沿断层走向位于断层右侧(BB′)5km处地表质点加速度时程曲线(下)(三维速度结构) Fig. 7A Time histories of particle velocities (upper) and accelerations (lower) observed on BB' line which is located on the right side of the fault with an off-set of 5 km away from fault trace (3D velocity model) |
|
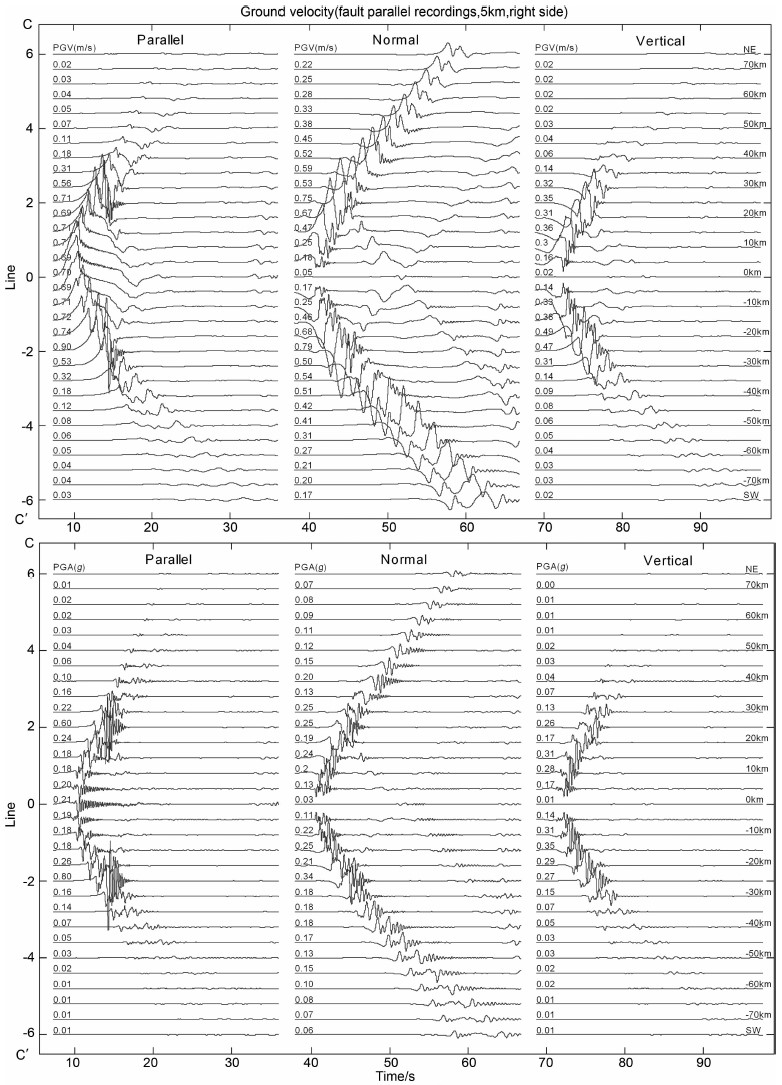
图 7B 沿断层走向位于断层左侧(CC′)5km处地表质点速度时程曲线(上);沿断层走向位于断层左侧(CC′)5km处地表质点加速度时程曲线(下)(三维速度结构) Fig. 7B Time histories of particle velocities (upper) and accelerations (lower) observed on CC' line which is located on right side of the fault with an off-set of 5 km away from fault trace (3D velocity model) |
|
图 8 唐山地震近场地表水平峰值加速度分布特征(a)三维速度结构;(b)一维速度结构;(c)唐山地震烈度分布图(数据来源:中国近代地震目录[37]) Fig. 8 Near-fault peak ground acceleration distribution (horizontal components) derived from current modeling, (a)3Dvelocity model, (b) lDvelocity model, and (c) Observed intensity distribution of the 1976 Tangshan Earthquake (Source: Modern Earthquake Catalogue of China[37]) |
通过对比一维速度结构和三维速度结构的模拟结果我们可以看出,速度结构横向上被平均之后,原来低速区变大了,原来高速区变小了,而得到的PGA是原来低速区较大的地方变小了,高速区加速度较小的区域变大了,那么根据这个结果我们可以定性地得到低速带的区域对地震波产生的影响较大,得到的质点运动的速度相对也会被加强,因此在做危害性评估时对低速带的区域也应该考虑相应地加大其抗震系数.
4.2 破裂方向性对地表运动的影响图 7中地表质点运动的平行断层和垂直断层分量存在着明显的区别,对平行分量而言,大振幅的质点运动主要集中在断层两侧,离开断层端点后,其振幅值迅速衰减.但是,垂直断层的水平分量质点运动的幅值则保持了相当缓慢的衰减过程(相对平行分量而言).其物理过程可归结于有限断层破裂方向性效应.
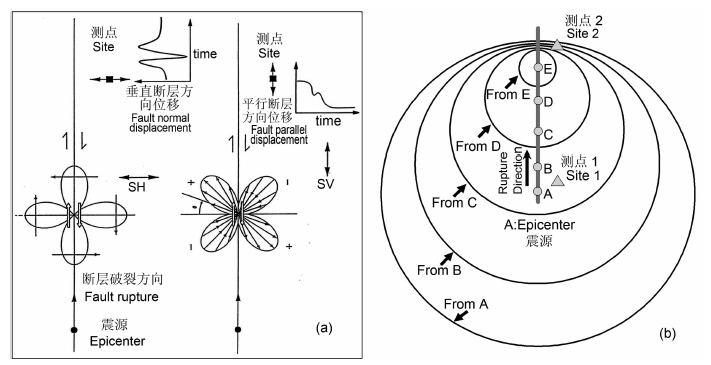
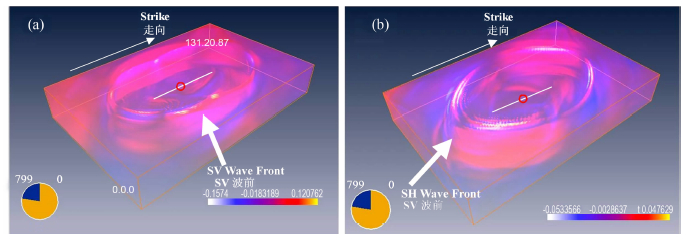
有限断层破裂传播方向性对地表运动的影响一直都是被大家广泛关注的问题,破裂传播的方向性作用是指地表运动在沿着破裂方向的前端区域会被加强,这些点与震中的连线与沿着断层破裂的方向有一个小的夹角[38, 39].对于大地震而言,我们知道在断层的附近一般会造成较大的破坏,但事实上,由于方向性作用的影响,在远离断层且与断层有一定角度的位置区域内也会造成较大的破坏.从目前模拟得到的地表运动特征,我们很清晰地看到了破裂传播方向性作用对地表运动所造成的影响.对于双向破裂的唐山地震,破裂在向东北和西南向传播时都有着十分明显的方向性作用,尤其是与断层垂直的速度分量表现的最为强烈,如图 7A和7B.事实上,对于走滑型断层而言,其地震波的辐射图案如图 9a所示,导致破裂传播方向性效应则来自质点运动时的SH波,其质点运动方向与断层相互垂直,而传播方向则与断层破裂方向(断层走向)一致.图 7采用可视化技术,得到了断层动态破裂瞬态时刻SV和SH分量速度场(图 10).从图中可知,沿断层走向,SH分量取值(垂直于断层的水平分量)在断层两端的前缘远远大于SV分量(平行于断层的水平分量),这为我们进一步认识地震波辐射过程及方向性对地表运动的影响提供了很直观的依据.同时也给我们一个启示,就是在进行工程抗震设计时不仅要在断层的附近加大抗震设防系数,同时由于破裂方向性的影响在断层破裂方向的前方且与断层走向有一定夹角的区域,也应相应地加大抗震设防的系数.
|
图 9 简化走滑断层破裂传播时P波和S波辐射图案和与之相对应的质点运动方式 (a)SH波同破裂传播方向一致,质点的振动方向与断层走向垂直,SH波的传播导致了破裂方向性的产生;(b)A为震中,破裂沿断层从A点向B,C,D和E传播,A,B,C,D,和E在不同时刻破裂,不同半径的圆圈表示了从不同破裂点S波辐射波前,位于断层上方场地/观测点(三角形)由于质点运动的叠加效应,场地运动量获得了增强. Fig. 9 The radiation pattern of P- & S-waves and particle motion mode that express (a) The propagation direction of SH wave is unanimous with the rupture direction, and the direction of partial motion is perpendicular with it. (b) Site A is the epicenter, rupture spreads along the fault from A to B, C, D and E, The ground motion is enhanced as a result of particle movement superimposed effect. |
|
图 10 断层动态破裂形成的瞬态速度场(单位:m/s) (a)平行于断层方向质点速度水平分力量;(b)垂直于断层方向质点速度水平分量.平行和垂直于断层的近断层质点运动分别对应了SV波和SH波的辐射和传播.图中实线为断层在地表的投影,圆圈为震中位置,图示时刻为地震发生后的第28.42s的瞬时状态. Fig. 10 The instantaneous particle velocity fields caused by dynamic fault rupture (in units of m/s) Particle velocity fields for Fig. 7A and 7B are correspondent of the fault-parallel and-normal components, respectively. Compared with fig. 7A, The :.ault-normal particle motions along the fault extending-direction indicated by SH Wave Front in fig. 7B become stronger due to the propagated rupture with associated SH-typed radiation in the horizontal direction. The circle and solid line are the assumed earthquake epicenter and fautt trace on the surface, respectively. |
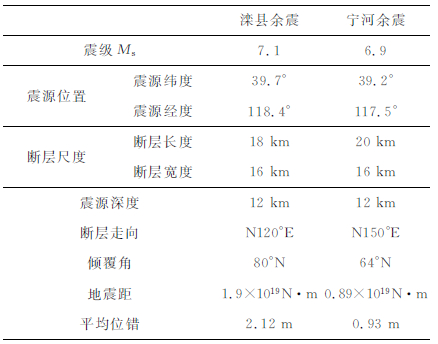
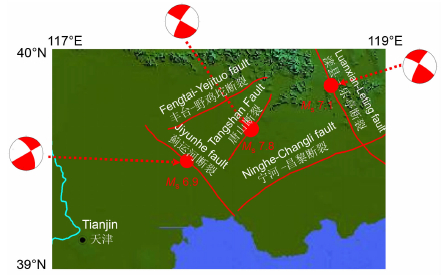
唐山大地震之后发生了一系列的余震,其中最大的余震是在主震发生15h后,在滦县附近发生的MS7.1级地震.第二个较大余震是1976年11月15日发生在西南宁河附近MS6.9级地震,该较大余震的发生加剧了灾害的严重性,对滦县,宁河大震级余震的研究有助于我们对华北地区潜在地震危险性的了解.根据Nebelek et al.等[40],张之立等[41],Huang和Yeh[35]研究结果,得到的滦县和宁河地震的震源参数如表 5所示.图 11为唐山主要断裂的分布图,图示中给出滦县和宁河两大余震的震源机制解,其表明滦县和宁河地震分别为近走滑断层地震.结合区域活动构造形变场特征,对于余震触发的物理机制的研究可为未来地震危险性分析提供重要的依据.
|
|
表 5 滦县余震和宁河余震震源参数 Table 5 Source parameters of the Luanxian aftershock and Ninghe aftershock |
|
图 11 唐山MS7.8级主震、MS7.1级滦县余震及MS6.9宁河余震的断层分布特征 Fig. 11 The spatial distribution of active faults related to the 1976 Tangshan Ms7.8 mainshock, Ms7.1 and Ms6.9 aftershocks |
对于主震对余震的触发机制目前主要还是从静态的应力调整进行研究.Robinson和Zhou[5]利用应力交互作用研究了唐山主震对余震的触发,认为唐山主震断层南段的破裂促使了北段破裂的产生,并且主震的发生对后续余震的发生起到正向的促使作用.刘桂萍等[1]运用三段主震破裂模型研究了唐山主震对3个余震区的弹性触发作用,发现主震有助于后续余震发生.万永革等[42]根据黏弹性力学模型模拟计算了唐山主震对余震的触发,提到95%的余震发生在库伦破裂应力变化增加的区域,滦县的余震在唐山主震产生的0.05~0.2 MPa库伦破裂应力变化的驱动下产生,宁河余震在唐山主震产生0.2 MPa库伦破裂应力变化的驱动下产生.根据静态的应力调整来研究主震对余震的调制作用均可表明主震对后续余震的发生有影响.
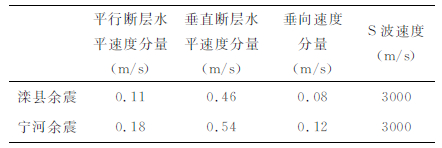
本文则试图通过所建立的动态破裂模型所得到的瞬时的动态应力变化,结合唐山地区的地质构造特征来解释唐山主震对余震的触发.有关余震动态应力触发的研究近期在国际上得到了广泛的重视,主要的形成机制包括了主震地震波辐射传播造成断层摩擦过程突变引起的库伦破裂失稳或地壳流体(地下水,岩浆)活动.Hough et al.[43]则从地壳形变率的角度讨论了余震动态应力触发可能的物理过程,强调了低形变率地区的较大余震动态触发的倾向性,这同区域内活动断层体系大都处于临界失稳状态可能相关.区域活动构造业已表明滦县和宁河地震发震断层分别位于沿唐山主震断层延伸方向的东北方向和西南方向.前面本文已经讨论了断层破裂传播的方向性使得沿断层走向及延伸方向地表质点水平运动分量(垂直于断层)得到极大的加强(图 7A和7B).表 6给出了滦县和宁河余震宏观震中处地表质点速度峰值.在平面波近似下,峰值动态应力σ同峰值质点运动速度v成正比,可写成:σ~μ/βv,μ和β分别为地壳介质剪切模量和横波速度.如果取μ=3.0×104 MPa,由震中参数和质点的振动速度代入公式(8),可以得到唐山主震发生后使得滦县余震在震中处沿错动方向产生的瞬时应力变化为2.0 MPa,沿逆冲方向的瞬时应力变化为0.1MPa,对于宁河余震,唐山主震的发生使得其在破裂点处沿走滑方向产生的瞬态应力变化为3.1 MPa,沿倾滑方向的瞬态应力变化为0.16 MPa,从图 11中看出滦县余震和宁河余震均近为走滑断层;从计算的结果来看,唐山主震对滦县余震的发震断层在走滑和倾滑方向上均产生了正向的促进作用,只是由于破裂方向性的影响使得在走滑方向的影响更大.结合唐山断裂带的特点,两个余震的发震断层近乎与主震断层垂直,如图 11.由于破裂的方向性影响,在余震的破裂点处唐山主震造成质点垂直于唐山主震断层的速度分量较大,这也是导致在断层的走滑方向上产生较大的瞬时应力变化的主要原因.
|
|
表 6 模拟计算结果所得滦县和宁河地震震中处质点峰值速度 Table 6 The peak ground velocities received in the epicenters of the 1976 Ms 7.1 Luanxian and Ms6.9 Ninghe events |
从断层双侧破裂模型出发,本文采用三维有限差分方法,模拟了1976年唐山地震的破裂过程和相应的近断层地表运动特征.结果显示,受地壳横向速度结构不均匀的影响,断层两端和两侧的地表运动呈明显的不对称性,地壳速度结构的低速层对地表质点的震动会带来更大的影响,使得断层西南端的质点速度和加速度总体大于断层东北端的质点速度和加速度,这同震后地震烈度分布特征一致.断层两侧地震动衰减速度也不相同,断层右侧,即断层的东南部分速度衰减较慢,断层左侧衰减较快;断层的端点速度和加速度均较大;受有限断层破裂传播方向性的影响,沿断层走向,垂直于断层走向的水平质点速度和加速度得到了较大的加强.并且,在断层两端的延伸方向,由SH波辐射造成的水平地表运动远远大于SV波辐射的影响.
研究的结果还表明,唐山主震的发生对其周围环境有一个同震动态应力调整,针对唐山地区的构造特点,得到主震对后续余震的发生起到了促发作用,峰值动态应力在断层的走滑方向上为2~3 MPa,在逆冲方向上为0.1~0.2 MPa.受破裂传播方向性的影响,导致这样大幅值应力变化的物理过程主要来自断层内部SH波的辐射和传播.因此,动态应力触发模式对滦县和宁河地震的发生提供了一种较合理的解释.需要指出的是,华北地区构造活动复杂,且地壳形变率较低,进一步探讨主震与余震之间的关系,即区域内大震是否总是伴随较大余震,对于华北地区的潜在地震危险性分析有着十分重要的意义.该研究结果对大震后余震危险性评估有一定的参考意义.如果对发生大地震地区的地质构造有一个清晰的了解,有详细的大震区断层及其滑动特性资料,本文提供的方法可以用来预测未来余震发生的位置及可能性.当然本文在模拟计算时把唐山地震理想化为垂直的走滑断层,这在一定程度会影响结果的精确性.尽管本文在完成的过程当中,我们尽量做到使模型更为合理,计算更为精确,但是由于受计算能力和研究资料不足等条件所限,论文中还是存在一些问题尚需进一步深入研究,如唐山地震资料少,精度低,不利于复杂震源模型的建立,没有考虑断层分段和空间的几何变化;模拟计算中没有考虑场地效应的影响;以及模拟结果中缺乏高频成分,这些工作将在接下来的工作中进一步去研究.
致谢在论文的完成过程中与周蕙兰教授,周仕勇教授,陈丽教授和Dr.Day进行了有益的讨论,在此一并表示感谢.同时也特别感谢于湘伟老师给提供的京津唐地区的三维速度结构,为我们工作开展提供了非常有力的支持,特此感谢!
| [1] | 刘桂萍, 傅征祥. 1976年7月28开唐山7.8级地震触发的区域地震活动和静应力场变. 地震学报 , 2000, 22(1): 17–26. Liu G P, Fu Z X. The seismicity and static stress change of the trigger area of 1976 Tangshan earthquake. Acta Seismologica Sinica (in Chinese) , 2000, 22(1): 17-26. |
| [2] | 张昭栋, 刘元生, 韩海华, 等. 唐山7.8级地震前后区域应力场的动态变化特征. 西北地震学报 , 2001, 23(2): 169–171. Zhang S D, Liu Y S, Han H H, et al. Dynamic change of regional stress field inverted by using water level data before and after the Tangshan MS7.8 Earthquake. Northwestern Seismological Journal (in Chinese) , 2001, 23(2): 169-171. |
| [3] | Dan K, Ishii T, Ebihara M. Estimation of strong ground motions in meizoseismal region of the 1976 Tangshan, China, earthquake. Bull.Seism.Soc.Am. , 1993, 83: 1756-1777. |
| [4] | Matsunami K, Zhang W. Estimation of seismic site response in the Tangshan area, China, using deep underground records. Bull.Seism.Soc.Am. , 2003, 93: 1065-1078. DOI:10.1785/0120020054 |
| [5] | Robinson R, Zhou S. Stress interactions within theTangshan, China, Earthquake Sequence of 1976. Bull.Seism.Soc.Am. , 2005, 95: 2501-2505. DOI:10.1785/0120050091 |
| [6] | 刘启方.基于运动学和动力学震源模型的近断层地震动研究[博士论文].哈尔滨:中国地震局工程力学研究所, 2005 Liu Q F.Studies on Near-fault ground motions based on kinematic and dynamic source models[Ph.D.dissertation].Harbin:Institute of Engineering Mechanics, China Earthquake Administration, 2005 http://www.oalib.com/references/18564543 |
| [7] | Hartzell S, Harmsen S, Frankel A, et al. Calculation of broadband time histories of ground motion:comparison of methods and validation using strong-ground motion from the 1994 Northridge earthquake. Bull.Seism.Soc.Am. , 1999, 89: 1484-1504. |
| [8] | Madariaga R, Olsen K, Archuleta R. Modeling dynamic rupture in a 3D earthquake fault model. Bull.Seismol.Soc.Am. , 1998, 88: 1182-1197. |
| [9] | Zhang W, Iwata T. Dynamic source rupture simulation of dipping faults with a 3D finite-difference method. AGU, Fall Meet.Suppl., Abstract , 2004, 85(47). |
| [10] | Zhang W B, Iwata T, Irikuraet K, et al. Dynamic rupture process of the 1999 Chi-Chi, Taiwan, earthquake. Geophys.Res.Lett. , 2004, 31: L10605. |
| [11] | Oglesby D D, Day S M. Fault geometry and the dynamics of the 1999 Chi-Chi (Taiwan) earthquake. Bull.Seismol.Soc.Am. , 2001, 91: 1099-1111. |
| [12] | Steven M Day, Dalguer Luis A. Comparison of finite difference and boundary integral solutions to threedimensional spontaneous rupture. J.Geophys.Res. , 2005, 110: B12307. DOI:10.1029/2005JB003813 |
| [13] | Zhang Haiming, Chen Xiaofei. Dynamic rupture process of the 1999 Chi-Chi, Taiwan, earthquake. Acta Seismologica Sinica , 2009, 22(1): 3-12. |
| [14] | Day S M. Three-dimensional finite difference simulation of fault dynamics:Rectangular faults with fixed rupture velocity. Bull.Seism.Soc.Am. , 1982, 72: 705-727. |
| [15] | Olsen K B, Day S M. TeraShake2:Spontaneous rupture simulations of Mw7.7 Earthquakes on the southern san andreas fault. Bull.Seism.Soc.Am. , 2008, 98: 1162-1185. DOI:10.1785/0120070148 |
| [16] | Olsen K B, Day S M, Minster J B. Strong shaking in los angeles expected from southern san andreasearthquake. Geophys.Res.Lett. , 2006, 33: L07305. |
| [17] | Day S M, Ely G P. Effect of a shallow weak zone on fault rupture. , numerical simulation of scale-model experiments.Bull.Seism.Soc.Am. , 2002, 92: 3022-3041. |
| [18] | 黄立人, 王学中, 刘天奎. 唐山地震前后的水平形变. 地震学报 , 1988, 10(4): 375–380. Huang L R, Wang X Z, Liu T K. The horizontal deformation of pre-seismic and post-seismic of Tangshan. Acta Seismologica Sinica (in Chinese) , 1988, 10(4): 375-380. |
| [19] | 刘洁, 宋惠珍, 巫映祥. 唐山地震发震断层运动学特征与大震重复周期. 地震学报 , 1997, 19(6): 566–573. Liu J, Song H Z, Wu Y X. The characteristic of Tangshan earthquake fault and recurrence repriod of large earthquake. Acta Seismologica Sinica (in Chinese) , 1997, 19(6): 566-573. |
| [20] | 蔡永恩, 何涛, 王仁. 1976年唐山地震震源动力过程的数值模拟. 地震学报 , 1999, 21(5): 469–477. Cai Y N, He T, Wang R. Modelling the source dynamic process of the 1976 Tangshan earthquake. Acta Seismologica Siniea (in Chinese) , 1999, 21(5): 469-477. |
| [21] | 谢礼力, 张敏政, 曲传军. 唐山主震近场地震动的模拟. 地震工程与工程振动 , 1994, 14(3): 1–10. Xie L L, Zhang M Z, Qu C J. Simulation of strong seismic motions for the Tangshan earthquake. Earthquake Engineering And Engineering Vibration (in Chinese) , 1994, 14(3): 1-10. |
| [22] | Cherry J T. A deterministic approach to the prediction of the frequency field ground motion and responmse spectra from stick-slip earthquakes. Earthquake Eng.Struct.Dynamics , 1976, 4: 315-332. DOI:10.1002/(ISSN)1096-9845 |
| [23] | Das S, Aki K. A numerical study of two-dimensional spontaneous rupture propagation. Geophys.J. , 1976, 50: 643-668. |
| [24] | Wu F T, Thomosn K C, Kuenzler H. Stick-slip propagation velocity and seismic source mechanism. Bull.Seism.Soc.Am. , 1972, 62: 1621-1628. |
| [25] | Hussenini M I, Jovanovich D B. The fracture energy of earthquake. Geophys.J. , 1975, 45: 367-385. |
| [26] | Madariaga R. Modeling of the three-dimensional earthquake faulting. Geophys.J. , 1977, 51: 625-651. DOI:10.1111/j.1365-246X.1977.tb04211.x |
| [27] | Ida Y. Cohesive force across the tip of a longitudinal shear crack and Grifith Specific surface Energy. J.Geophys.Res. , 1972, 77: 3796-3805. DOI:10.1029/JB077i020p03796 |
| [28] | Andrews D J. Rupture velocity of plane strain shear cracks. J.Geophys.Res. , 1976, 81: 5679-5687. DOI:10.1029/JB081i032p05679 |
| [29] | Dieterich J H. Time dependent friction and mechanics of stick-slip. Pure Appl, Geophys. , 1978, 116: 790-806. DOI:10.1007/BF00876539 |
| [30] | Dalguer L A, Day S M. Comparison of fault representation methods in finite difference simulations of dynamic rupture. Bull.Seism.Soc.Am. , 2006, 92: 1764-1778. |
| [31] | 陈运泰, 林邦慧, 王新华, 等. 用大地测量资料反演1976年唐山地震的位错模式. 地球物理学报 , 1979, 22(3): 201–216. Chen Y T, Lin B H, Wang X H. The inversion of dislocation-mode of the 1976 Tangshan earthquake with the geodetic data. Chinese J.Geophys. (in Chinese) , 1979, 22(3): 201-216. |
| [32] | Butler R, Stewart G S, Kanamori H, et al. The July 27, 1976 Tangshan, China earthquake-A complex sequence of interpolate events. Bull.Seism.Soc.Am. , 1979, 69(1): 207-220. |
| [33] | 周蕙兰. 浅源走滑大震震源过程的某些特征. 地球物理学报 , 1985, 28(6): 579–587. Zhou H L. The characteristics of strike-slip earthquake with low epicenter. Chinese J.Geophys. (in Chinese) , 1985, 28(6): 579-587. |
| [34] | Xie X B, Yap Z X. The faulting process of Tangshan earthquake inverted simultaneously from teleseismic waveforms and geodetic deformation. Phys Earth Planet Inter , 1991, 66: 265-277. DOI:10.1016/0031-9201(91)90081-R |
| [35] | Huang B S, Yeh Y T. The fault rupture of the 1976 Tangshan earthquake sequence inferred from coseismic crustal deformation. Bull.Seism.Soc.Am. , 1997, 87: 1046-1057. |
| [36] | 于湘伟, 陈运泰, 王培德. 京津唐地区中上地壳三维P波速度结构. 地震学报 , 2003, 25(1): 1–14. Yu X W, Chcn Y T, Wang P D. Three-dimensional P wave velocity structure in Beijing-Tianjing-Tangshan area. Acta Seismologica Sinica (in Chinese) , 2003, 25(1): 1-14. |
| [37] | 中国近代地震目录. 中国地震局震害防御司编. 北京: 中国科学技术出版社, 1999 . The Catalog of Modern Earthquake of China. Department of the Persistence of Earthquake Disaster (in Chinese). 1999 . |
| [38] | Somerville, Somerville P G. Magnitude scaling of the near fault rupture directivity pulse. Phys.Earth.Planetary.Int , 2003, 137: 201-212. DOI:10.1016/S0031-9201(03)00015-3 |
| [39] | Day S M, Gonzalez S H. Scale-model and numerica simulations of near-fault seismic directivity. Bull.Seism.Soc.Am. , 2008, 98: 1186-1206. DOI:10.1785/0120070190 |
| [40] | Nabelek J, Chen W P, Ye H.The Tangshan earthquak, sequence and its implications for the evolution of the North China basin.J.Geophys.Res., 92, 12615-12628 |
| [41] | 张之立, 王成宝, 方兴, 等. 唐山地震破裂过程的雁行断裂模式及理论和试验的模拟. 地震学报 , 1989, 11(3): 291–302. Zhang Z L, Wang C B, Fang X, et al. An echelon fraeture model for the Tangshan earthquake sequence as well as simulation in theory and experiment. Acta Seismologica Sinica (in Chinese) , 1989, 11(3): 291-302. |
| [42] | 万永革, 沈正康, 曾跃华, 等. 唐山地震序列应力触发的牯弹性力学模型研究. 地震学报 , 2008, 30(6): 581–593. Wang Y G, Shen Z K, Zeng Y H, et al. Study on viscelastic stress triggering model of the 1976 Tangshar earthquake sequence. Acta Seismologica Sinica (in Chinese) , 2008, 30(6): 581-593. |
| [43] | Hough S E, Leonardo Seeber, Armbruster J G. Intraplate triggered earthquakes:observations and interpretation. Bull.Seism.Soc.Am. , 2003, 93(5): 2212-2221. DOI:10.1785/0120020055 |
 2010, Vol. 53
2010, Vol. 53