地层内部由于受非均匀应力、热对流、温差以及物质迁移等多种因素影响,往往会引起地层电性、磁性以及热力学性质的各向异性.在石油测井中,电性各向异性的探测与研究对储层解释和评价有着十分重要的意义.当前各种常规电测井仪器只能测量到某一方向的电阻率分量,这给各向异性储层的正确解释和评价带来了困难[1].多分量感应测井(MCIL)仪器利用三个相互正交的发射线圈(Tx、Ty和Tz)和三个相互正交的接收线圈(Rx、Ry和Rz)同时测量九个磁场分量(Hxx、Hyy、Hzz、Hxy、Hyx、Hxz、Hzx、Hyz和Hzy),其测量结果正好构成一个完整的并矢Green函数,这将更加有利于解释和评价各向异性地层中的测井资料[2~8].然而在整个地球物理领域,目前对层状各向异性问题的研究主要采用如下两种模型:具有垂直对称轴的横向同性(TIV)模型[9~14]和具有水平对称轴的横向同性(又称方位各向异性Azimuthal Anisotropy)模型[15~20].这两种模型都只有一个旋转对称轴,人们利用传输线理论(TLM)、Hertz势理论以及模式匹配算法(NMM)等已经对横向同性模型中的多分量感应测井响应进行了深入研究[6~8].但是对于更为一般的完全各向异性地层中的测井响应,现有的报道却非常少.为充分利用多分量感应测井仪器提供的丰富电磁场资料解决更为复杂的地质问题,本文以具有双轴对称性的正交各向异性(Orthogonal Anisotropy)[21, 22]介质为基本模型,通过传播矩阵算法研究并建立了层状正交各向异性地层中多分量感应测井响应的数值模拟算法.最后通过数值模拟结果分别考察了各向异性系数、仪器长度、发射源频率以及井眼倾角变化时,多分量感应测井响应的特征和变化规律.
传播矩阵法作为一种处理层状介质中波传播问题的有效手段,已被广泛应用在光学、等离子物理学以及地球物理学等领域[23~27].目前该算法的推导过程较为繁琐,不利于理解和掌握.本文通过以下方法对其推导过程进行了改进:首先将均匀介质中上行波和下行波模式的求解表示成一阶常微分方程的边值问题,使电磁波求解更加容易;然后在求解层状地层中电磁波模式的解析表达式时,利用叠加原理和边界条件给出了更为简洁的广义反射系数和电磁波振幅的递推公式,避免了由多个矩阵直接相乘导致的大指数项问题,整个算法更容易在计算机上实现.
2 理论与方法 2.1 Maxwell方程的模式分解
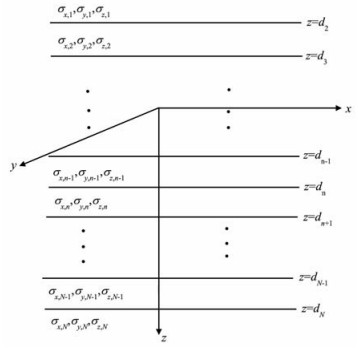
假定地层模型由N个水平层状正交各向异性地层组成(图 1),各个地层的界面位置用向量dn(n=2,3,…,N)表示,电导率用对角张量σ=diag(σxn,σyn,σzn)(n=1,2,…,N)表示,其中σxn,σyn和σzn分别表示第n个地层三个主轴方向上的电导率分量.用M=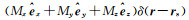
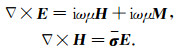
|
(1) |
|
图 1 水平层状正交各向异性地层模型 Fig. 1 Model of a horizontally layered orthorhombic anisotropy formation |
由于地层电导率函数σ与坐标变量x和y无关,对方程(1)中的电磁场关于变量x和y进行Fourier变换
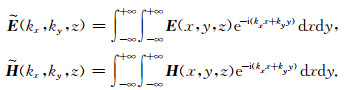
|
由直角坐标系下旋度算子“ Δ × ”的张量形式和傅氏变换微分定理,频率波数域中的旋度算子可表示为
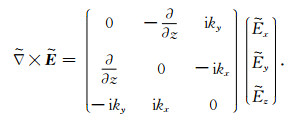
|
将上式代入方程(1)中,引入水平慢度变量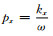
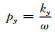
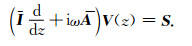
|
(2) |
其中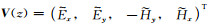
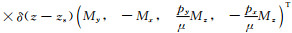

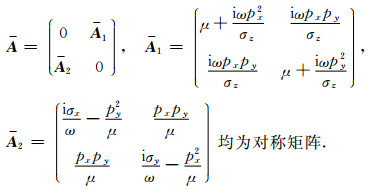
|
而电磁场的垂直分量与水平分量满足如下关系
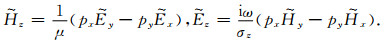
|
(3) |
方程(2)是关于矢量V(z)的一阶线性微分方程组,其解可分解成上行波和下行波模式的组合.首先利用本征值理论将矩阵A表示为
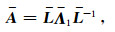
|
(4) |
其中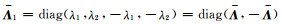
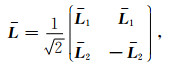
|
(5) |
其逆矩阵
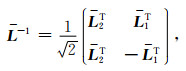
|
(6) |
本征值和本征向量的具体求解见附录A.
将(4)式代入方程(2)中,令电磁波模式W(z)=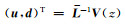
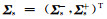
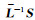
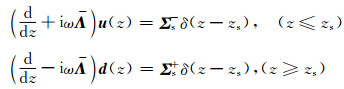
|
(7) |
其中
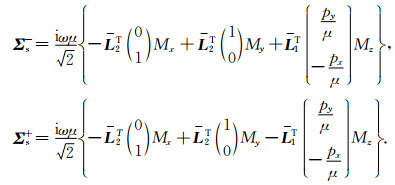
|
(8) |
在均匀正交各向异性介质中,由于不存在反射界面,方程(7)中由Σs-和Σs+产生的上行波u和下行波d分别满足条件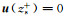
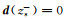
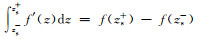
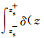
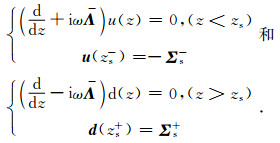
|
(9) |
求解方程(9),可得均匀正交各向异性介质中上行波和下行波的解析表达式:
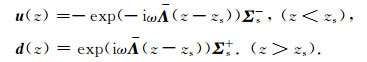
|
(10) |
对于层状正交各向异性地层,用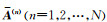
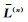
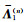
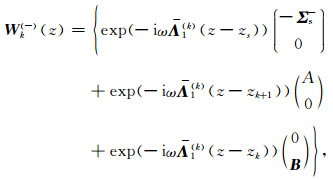
|
(11) |
而在区域zs < z < zk+1中,电磁波模式的表达式为
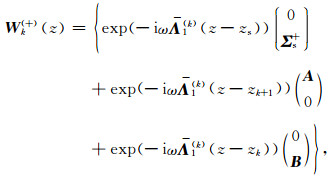
|
(12) |
其中A和B均为2阶列向量,分别表示下界面和上界面上反射波的振幅.
利用波场传播理论[30]可知,A等于入射到界面z=zk+1上的整个下行波的反射
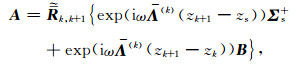
|
(13) |
而B等于入射到界面z=zk上的整个上行波的反射
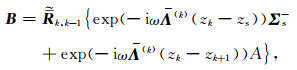
|
(14) |
其中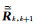
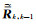
求解方程(13)和(14)得
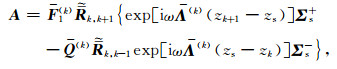
|
(15) |

|
(16) |
其中
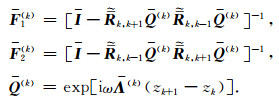
|
(17) |
将(15)~(17)式代入(11)和(12)式,经整理可得发射源所在层的电磁波模式表达式
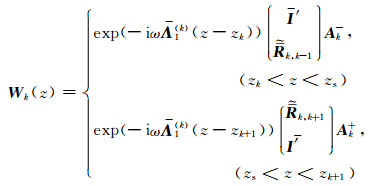
|
(18) |
其中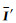

|
(19) |
均为2阶列向量,表示该层中电磁波的振幅.
当源Σs位于顶层时,由于没有上界面,(11)和(12)式中的B=0.介质1中的电磁波模式可简化为
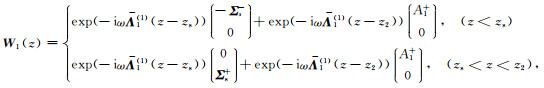
|
(20) |
其中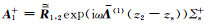
当源Σs位于底层时,只需令(11)和(12)式中的A=0,即可得到类似于上面的电磁波模式简化表达式.
对于发射源Σs以外的其他地层,电磁波模式也具有类似(18)式的解析形式
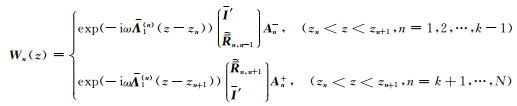
|
(21) |
其中An+和An-分别表示位于发射源所在层(k)下部和上部的各个地层中的电磁波振幅.当n=1时,假设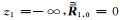
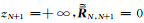
下面进一步确定(18)~(21)式中的电磁波振幅以及广义反射系数.首先考虑n≥k时,由(21)式可将第n+1层中的电磁波模式表示为

|
显然,在界面z=zn+1上,第n+1层中的下行波是该层中的上行波的反射与第n层中的下行波的透射的叠加:
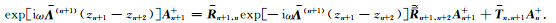
|
同样,第n层中的上行波是该层中的下行波的反射与第n+1层中的上行波的透射的叠加:
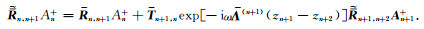
|
求解上面两式可得电磁波振幅An+1+和广义反射系数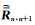
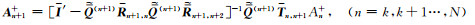
|
(22) |
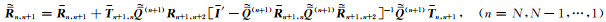
|
(23) |
其中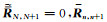
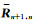
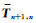
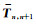
采用类似的方法可得n≤k时,电磁波振幅An-1-和广义反射系数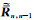

|
(24) |
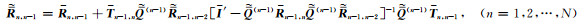
|
(25) |
其中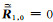
由各个地层中的电磁波模式W(z)解析表达式和方程V(z)=LW(z),可得频率波数域中的电磁场水平分量
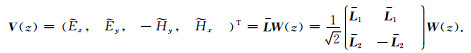
|
(26) |
再通过(3)式即可确定频率波数域中的电磁场垂直分量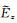
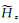
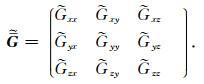
|
通过如下Fourier逆变换

|
(27) |
即可得到频率空间域中的磁场并矢Green函数.由于(27)式是二维无限平面上的广义积分,为了保证计算精度和运算效率,采用二维Patterson自适应求积算法结合有限连分式展开技术[31~33]专门开发了相应的计算软件.
为了考察不同倾斜井眼情况下的多分量感应测井响应,需要将上面地层坐标系XYZ下的计算结果转化到仪器坐标系X'Y'Z'[2].设井眼(即Z'轴)与Z轴的夹角为α,OX'Z'平面与OXY平面垂直且与OXZ平面的夹角为θ.利用坐标旋转可得仪器坐标系X'Y'Z'与地层坐标系XYZ间的旋转矩阵
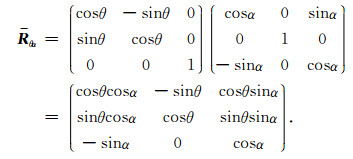
|
这样,仪器坐标系下的磁场并矢Green函数可表示为
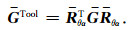
|
(28) |
多分量感应测井主要是通过测量二次场产生的感生电动势[6]来探测地层电导率的空间分布和不同方向上的电导率大小,所以其响应特征主要与磁场并矢Green函数的虚部(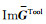
本节采用前面提出的PMM算法具体考察正交各向异性地层中多分量感应仪器的测井响应,用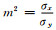
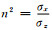
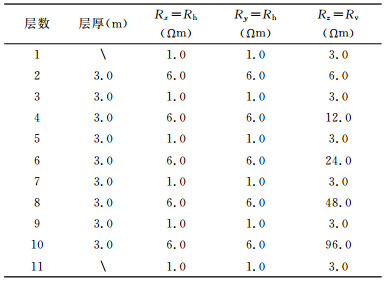
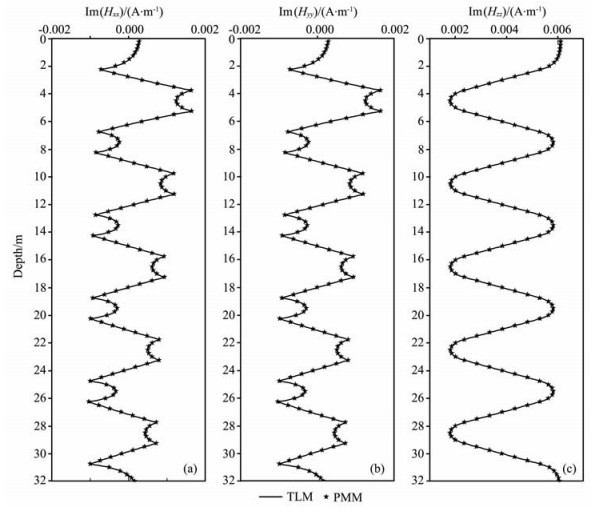
为检验PMM算法的有效性和计算精度,在TIV模型上对比给出PMM算法和TLM算法的数值模拟结果.令σx=σy=σh,σz=σv,地层模型参数见表 1.图 2给出了垂直井眼情况下发射源频率f=20kHz,仪器长度L=1.5 m时,由两种不同算法计算得到的磁场强度主分量曲线(Hxx、Hyy和Hzz).观察该图可以看到两者吻合的非常好,说明用PMM算法计算测井响应是可行的,并且其计算结果的精度也是较高的.
|
|
表 1 TIV模型地层模型参数 Table 1 Model parameters of TIV model |
|
图 2 在TIV模型上PMM和TLM算法计算结果的对比 (a)Hxx;(b)Hyy;(c)Hzz.α=0°,f=20kHz,L=1.5m. Fig. 2 The comparison of results obtained by PMM and TLM in a TIV model |
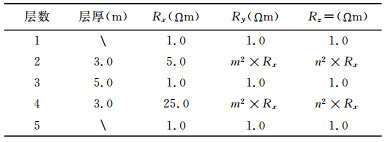
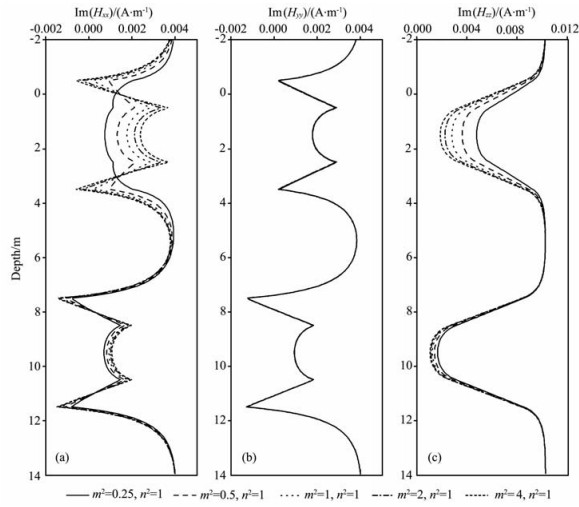
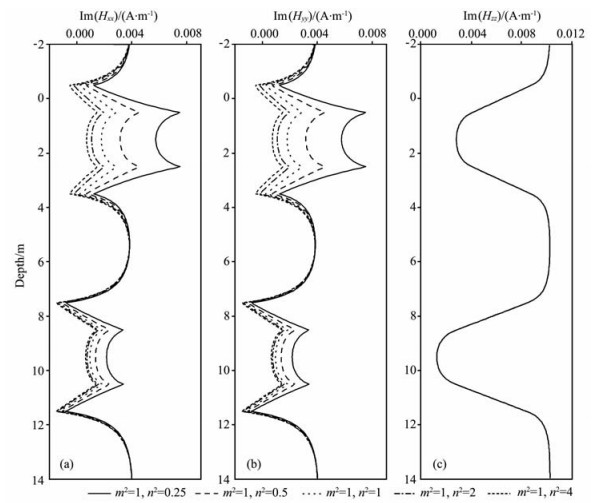
为考察各向异性对测井响应的影响,建立如下模型,地层模型参数见表 2.图 3给出了垂直井眼情况下,发射源频率f=20kHz,仪器长度L=1.0m,垂直各向异性系数n2=1.0,水平各向异性系数m2=0.25,0.5,1.0,2.0,4.0时,测井响应的计算结果.从图中可以看到:磁场强度y轴响应Hyy不受水平各向异性系数m2变化的影响,而x轴响应Hxx随m2的增大而增大,z轴响应Hzz随m2的增大而减小,并且测井响应在低阻层受水平各向异性系数变化的影响比在高阻层明显;此外,磁场强度的x轴和y轴响应在层界面附近较为复杂,出现“犄角”现象,而z轴响应相对简单,无“犄角”现象出现.“犄角”现象的产生,主要是由于层界面附近积累了大量面电荷导致的,随着水平各向异性系数的减小,x轴响应的“犄角”逐渐消失,说明层界面上的面电荷随地层y轴电导率的增大而减少.同样,图 4给出了水平各向异性系数m2=1.0,垂直各向异性系数n2=0.25,0.5,1.0,2.0,4.0时,测井响应的计算结果.观察图 4发现:磁场强度z轴响应Hzz不受垂直各向异性系数n2变化的影响,图形较为简单,而x轴和y轴响应完全相同,且随垂直各向异性系数的增大而减小,图形较为复杂,出现“犄角”现象.
|
|
表 2 各向异性地层模型参数 Table 2 Model parameters of anisotropic model |
|
图 3 水平各向异性系数(m2)变化对测井响应的影响 (a)Hxx;(b)Hyy;(c)Hzz.α=0°,f=20kHz,L=1.0m. Fig. 3 The influence of change in horizontal anisotropy coefficients (m2) on the responses of MCIL tool |
|
图 4 垂直各向异性系数(n2)变化对测井响应的影响 (a)Hxx;(b)Hyy;(c)Hzz.α=0°,f=20kHz,L=1.0m. Fig. 4 The influence of change in vertical anisotropy coefficients (n2) on the responses of MCIL tool |
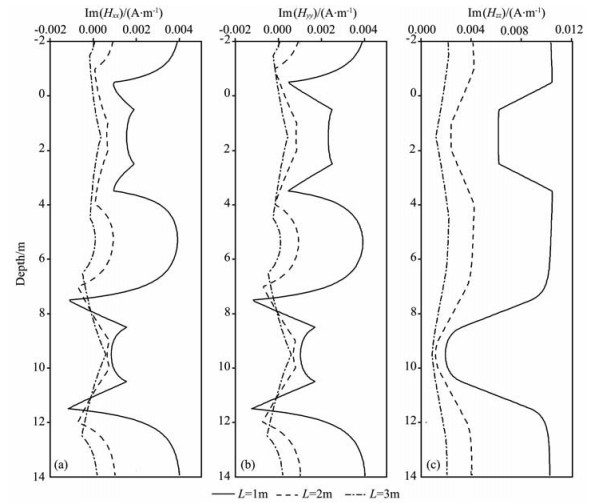
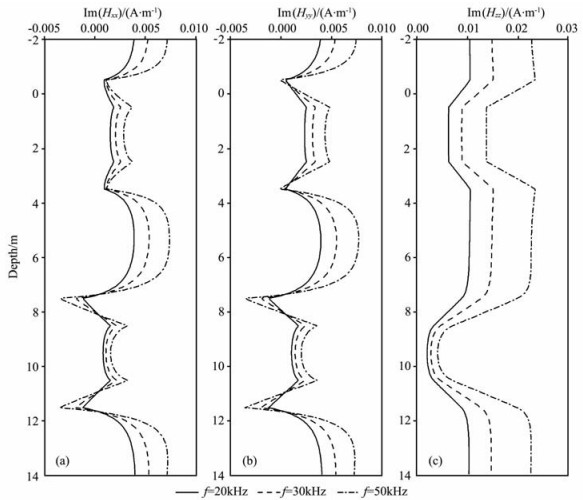
采用与3.2节相同的地层模型,将电阻率地层的水平各向异性系数(m2)和垂直各向异性系数(n2)分别取为0.5和2.0.图 5给出了垂直井眼情况下发射源频率f=20kHz,仪器长度L=1.0,2.0,3.0m时,测井响应的计算结果.可以看到:随着仪器长度的增大,响应曲线的纵向分辨率逐渐降低.图 6又给出了垂直井眼情况下,仪器长度L=1.0 m,发射源频率f=20,30,50kHz时,测井响应的计算结果.观察发现:发射源频率的增大将导致测井响应的增大,这是由于趋肤效应增强造成的.
|
图 5 仪器长度(L)变化对测井响应的影响 (a)Hxx;(b)Hyy;(c)Hzz.m2=0.5,n2=2.0,α=0°,f=20kHz. Fig. 5 The influence of change in tool lengths (L) on the responses of MCIL tool |
|
图 6 发射源频率(f)变化对测井响应的影响 (a)Hxx;(b)Hyy;(c)Hzz.m2=0.5,n2=2.0,α=0°,L=1.0m. Fig. 6 The influence of change in work frequencies (f) on the responses of MCIL tool |
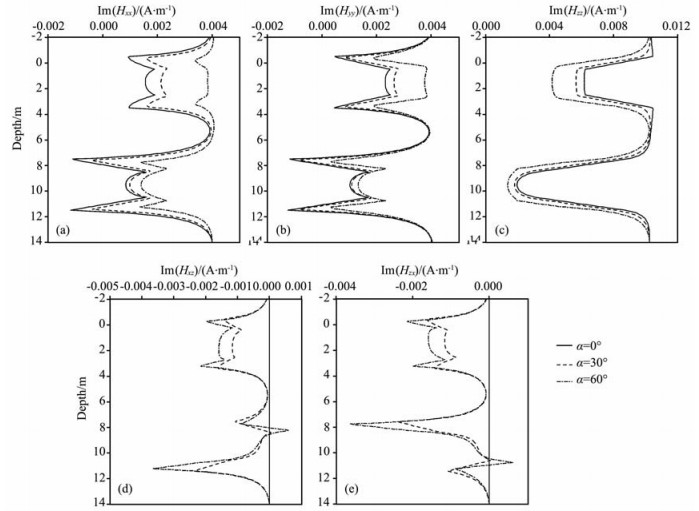
仍采用3.3小节的地层模型,图 7给出了发射源频率f=20kHz,仪器长度L=1.0 m,井眼倾角α=0°,30°,60°时,测井响应的计算结果.从图中可以明显看到:当井眼倾角不为零时,垂直磁偶极子Mz在水平x方向以及水平磁偶极子Mx在垂直z方向上均产生负响应,即磁场强度分量Hxz和Hzx不再为零;响应曲线除Hzz外,Hxx、Hyy、Hxz和Hzx均在层边界附近出现“犄角”现象,且“犄角”现象在高阻层比在低阻层更明显;随着井眼倾角的增大,磁场强度分量Hxx和Hyy不断增大,Hzz、Hxz和Hzx不断减小.以上结果表明:在井眼倾斜时,测井响应是地层三个主轴方向电导率的综合反映.这就增大了实际资料处理和解释的难度,要想从测井曲线中提取出三个主轴方向上的电导率,需要借助特殊的反演手段.
|
图 7 井眼倾角(α)变化对测井响应的影响 (a)Hxx;(b)Hyy;(c)Hzz;(d)Hxz;(e)Hzx.m2=0.5,n2=2.0,f=20kHz,L=1.0m. Fig. 7 The influence of change in dipping angles (α) on the responses of MCIL tool |
本文通过传播矩阵理论推导出层状正交各向异性地层中多分量感应测井响应的正演模拟公式.将均匀介质中的电磁波求解问题表示成一阶常微分方程的边值问题,使电磁波模式的求解更加容易;由递推公式给出多层介质的广义反射系数和电磁波振幅,避免了计算多个矩阵的直接相乘;采用二维Patterson自适应求积算法结合有限连分式展开技术计算傅氏逆变换,提高了运算效率和计算精度.通过考察不同各向异性系数、不同井眼倾角以及仪器长度和工作频率变化时的多分量感应测井响应特征发现:水平各向异性系数的变化不改变y轴的测井响应,垂直各向异性系数的变化不改变z轴的测井响应;仪器长度的增大导致测井响应纵向分辨率的降低;发射源频率的增大又会造成趋肤效应的增强;井眼倾角的变化不但影响测井响应的三个主轴分量,还将产生x轴和z轴方向的负响应.最后需要指出的是,本文只考虑了分层均匀介质的正演模拟,对于含有井眼和侵入带的测井响应正演,以及提取地层真实电导率的反演技术,将是日后有待研究的新课题.
|
|
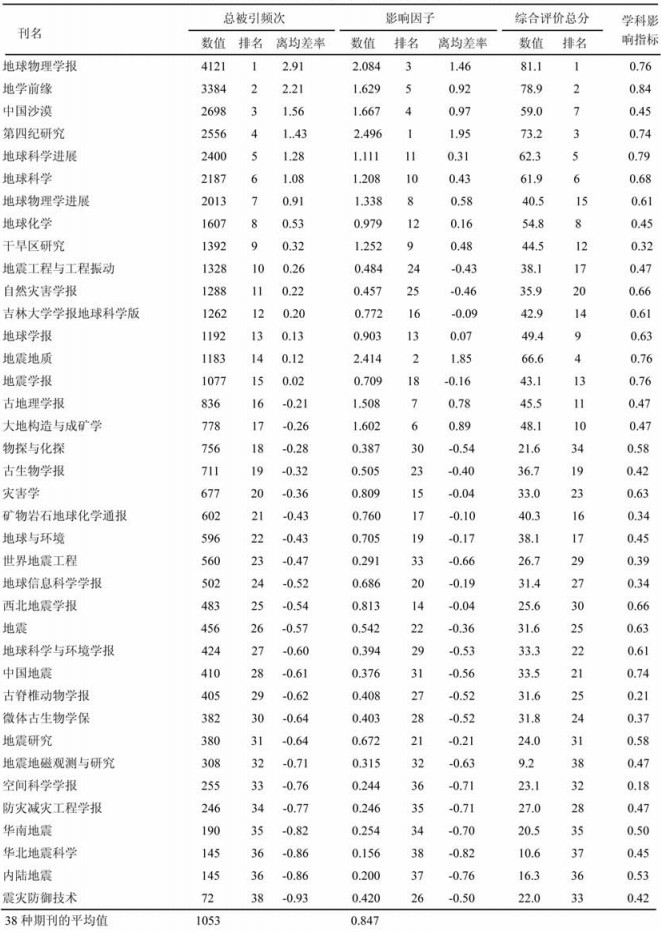
表 2009年地球科学类期刊主要指标(引自CSTPCD) |
矩阵A的本征值由如下方程确定
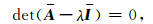
|
(A1) |
这涉及到求解关于本征值λ的一元四次方程[34].对于正交各向异性介质,由于矩阵A是斜对角的分块矩阵,其本征值具有如下的简单解析表达式
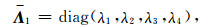
|
(A2) |
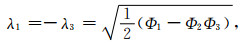
|
(A3) |
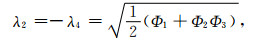
|
(A4) |
其中
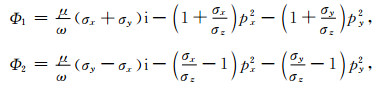
|
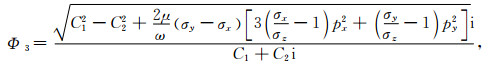
|
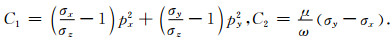
|
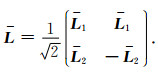
|
(A5) |
将(A2~A5)式代入方程(4),经一系列运算得
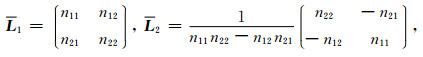
|
其中
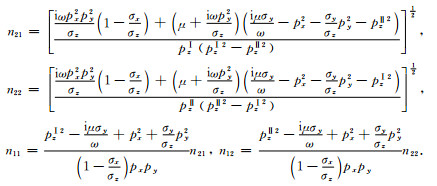
|
对于只有一个界面的2层模型,设层界面位置z=z1,与介质1和介质2对应的系数矩阵的本征值和归一化本征向量矩阵分别为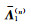
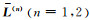
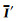
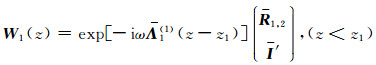
|
(B1) |
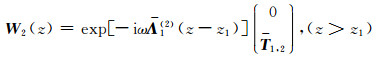
|
(B2) |
其中R1,2和T1,2分别表示界面z=z1的反射系数和透射系数,它们都是2×2阶矩阵.
利用电磁场水平分量V(z)=LW(z)在界面z=z1上连续,结合方程(B1)和(B2)可得反射系数R1,2和透射系数T1,2满足下面的方程
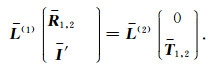
|
(B3) |
求解上式得
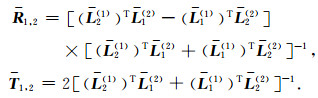
|
(B4) |
同理,假设在介质2中有一个向上入射的单位电磁波I',遇到界面z=z1后发生反射和透射,可得另一组反射系数R2,1和透射系数T2,1的表达式
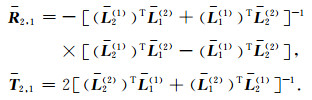
|
(B5) |
| [1] | 汪宏年, 杨善德, 王艳. 各向异性地层中电阻率测井的响应特征. 石油地球物理勘探 , 1999, 34(6): 649–656. Wang H N, Yang S D, Wang Y. The response characteristic of resistivity log in anisotropic formations. Oil Geophys. Prospect.(in Chinese) (in Chinese) , 1999, 34(6): 649-656. |
| [2] | Zhdanov S, Kennedy D, Peksen E. Foundations of tensor induction well-logging. Petrophysics , 2001, 42(6): 588-610. |
| [3] | Kriegshiuser B, Fanini O, Forgang S, et al. A new multi-component induction logging tool to resolve anisotropic formations. Transaction of the SPWLA 41st. Ann. Log. Symp., 2000, paper D |
| [4] | Miyairi S, Kashihara K, Sato M, et al. Directional induction logging methods. SPWLA 35th Ann. Log. Symp., 1994, paper AA |
| [5] | Zhdanov M S, Kennedy W D, Cheryauka A B, et al. Principles of the tensor induction well-logging in a deviated well in an anisotropic medium. SPWLA 42nd. Ann. Log. Symp., 2001, paper R |
| [6] | Wang H N, So P, Yang S W, et al. Numerical modeling of multicomponent induction well-logging tools in the cylindrically stratified anisotropic media. IEEE Trans. on Geosci. and Remote Sensing , 2008, 46(4): 1134-1146. DOI:10.1109/TGRS.2008.915748 |
| [7] | Wang H N, Tao H G, Yao J J, et al. Fast multiparameter reconstruction of multicomponent induction well logging datum in deviated well in a horizontally stratified anisotropic formation. IEEE Trans. on Geosci. and Remote Sensing , 2008, 46(5): 1525-1534. DOI:10.1109/TGRS.2008.916080 |
| [8] | 汪宏年, 陶宏根, 姚敬金, 等. 用模式匹配算法研究层状各向异性倾斜地层中多分量感应测井响应. 地球物理学报 , 2008, 51(5): 1591–1599. Wang H N, Tao H G, Yao J J, et al. Study on the response of a multicomponent induction logging tool in deviated and layered anisotropic formations by using numerical mode matching method. Chinese J. Geophy. (in Chinese) , 2008, 51(5): 1591-1599. |
| [9] | Schoenberg M. Reflection of elastic waves from periodically stratified media with interfacial slip. Geophysical Prospecting , 1983, 31(2): 265-292. DOI:10.1111/gpr.1983.31.issue-2 |
| [10] | 孙向阳, 聂在平, 赵延文, 等. 用矢量有限元方法模拟随钻测井仪在倾斜各向异性地层中的电磁响应. 地球物理学报 , 2008, 51(5): 1600–1607. Sun X Y, Nie Z P, Zhao Y W, et al. The electromagnetic modeling of logging-while-drilling tool in tilted anisotropic formations using vector finite element method. Chinese J. Geophy. (in Chinese) , 2008, 51(5): 1600-1607. |
| [11] | 陈桂波, 汪宏年, 姚敬金, 等. 用积分方程法模拟各向异性地层中三维电性异常体的电磁响应. 地球物理学报 , 2009, 52(8): 2174–2181. Chen G B, Wang H N, Yao J J, et al. Modeling of electromagnetic responses of 3-D electrical anomalous body in a layered anisotropic earth using integral equations. Chinese J. Geophy. (in Chinese) , 2009, 52(8): 2174-2181. |
| [12] | 沈金松, 郭乃川. 各向异性层状介质中视电阻率与磁场响应研究. 地球物理学报 , 2008, 51(5): 1608–1619. Shen J S, Guo N C. Study on the apparent resitivity and magnetic field responses of a layered earth with arbitrary anisotropy. Chinese J. Geophy. (in Chinese) , 2008, 51(5): 1608-1619. |
| [13] | 郑海山, 张中杰. 横向各向同性(VTI)介质中非线性地震波场模拟. 地球物理学报 , 2005, 48(3): 660–671. Zheng H S, Zhang Z J. Synthetic seismograms of nonlinear seismic wave in anisotropic (VTI) media. Chinese J. Geophy. (in Chinese) , 2005, 48(3): 660-671. |
| [14] | Yang D H, Teng J W, Zhang Z J, et al. A nearly analytic discrete method for acoustic and elastic wave equation in anisotropic media. Bulletin of the Seismological Society of America , 2003, 93(2): 882-890. DOI:10.1785/0120020125 |
| [15] | Crampin S. Effective anisotropic elastic constants for wave propagation through cracked solids. Geophys. J. R. Arstr. Soc. , 1984, 76(1): 135-145. DOI:10.1111/j.1365-246X.1984.tb05029.x |
| [16] | 阮爱国, 毛桐恩, 李清河, 等. 层状方位各向异性介质的视电阻率计算. 地震学报 , 2002, 24(5): 502–509. Ruan A G, Mao T E, Li Q H, et al. Apparent resistivity of azimuthal anisotropy layered media. Acta Seismologica Sinica (in Chinese) , 2002, 24(5): 502-509. |
| [17] | Li X B, Pedersen L B. The electromagnetic response of an azimuthally anisotropic half-space. Geophysics , 1991, 56(9): 1462-1473. DOI:10.1190/1.1443166 |
| [18] | Zhang Z J, Teng J W, He Z H. Azimuthal anisotropy of seismic velocity, attenuation and Q value in viscous EDA media. Science in China (Series E) , 2000, 43(1): 17-22. |
| [19] | Zhang Z J, Wang G J, Harris J M. Multi-component wavefield simulation in viscous extensively dilatancy anisotropic media. Physics of the Earth and Planetary Interiors , 1999, 114: 25-38. DOI:10.1016/S0031-9201(99)00043-6 |
| [20] | 杜启振, 杨慧珠. 方位各向异性黏弹性介质波场有限元模拟. 物理学报 , 2003, 52(8): 2010–2014. Du Q Z, Yang H Z. Finite-element methods for viscoelastic and azimuthally anisotropic media. Acta Physica Sinica (in Chinese) , 2003, 52(8): 2010-2014. |
| [21] | 阮爱国, 李清河. 地壳介质各向异性电性本构关系讨论. 华南地震 , 1999, 19(3): 35–42. Ruan A G, Li Q H. Electric property constitutive relation of anisotropic crustal media. South China Journal of Seismology (in Chinese) , 1999, 19(3): 35-42. |
| [22] | Waff S. Theoretical considerations of electrical conductivity in a partially molten mantle and implications for geothermometry. J. Geophys. Res. , 1974, 79(26): 4003-4010. DOI:10.1029/JB079i026p04003 |
| [23] | Kopp V I, Zhang Z Q, Genack A Z. Lasing in chiral photonic structures. Progress in Quantum Electronics, 2003 |
| [24] | Campos A, Hu B L. Non-equilibrium dynamics of a thermal plasma in a gravitational field. Physical Review D, 1998, Arxiv:9805485v2 |
| [25] | 阎贫, 何樵登. 横观各向同性介质中的传播矩阵及其应用. 地球物理学报 , 1994, 37(Suppl.): 404–412. Yan P, He Q D. Propagating matrix and its application in transversely isotropic media. Acta Geophysica Sinica (in Chinese) , 1994, 37(Suppl.): 404-412. |
| [26] | 郑宏兴, 葛德彪. 广义传播矩阵法分析分层各向异性材料对电磁波的反射透射. 物理学报 , 2000, 49(9): 1702–1706. Zheng H X, Ge D B. Electromagnetic wave reflection and transmission of anisotropic layered media by generalized propagation matrix method. Acta Physica Sinica (in Chinese) , 2000, 49(9): 1702-1706. |
| [27] | Stovas A, Ursin B. Reflection and transmission responses of layered transversely isotropic viscoeleastic media. Geophys. Prospect. , 2003, 51: 447-477. DOI:10.1046/j.1365-2478.2003.00381.x |
| [28] | Løseth L O, Ursin B. Electromagnetic fields in planarly layered anisotropic media. Geophys. J. Int. , 2007, 170: 44-80. DOI:10.1111/gji.2007.170.issue-1 |
| [29] | Ursin B. Review of elastic and electromagmetic wave propagation in horizontally layered media. Geophysics , 1983, 48: 1063-1081. DOI:10.1190/1.1441529 |
| [30] | Chew W C著.非均匀介质中的场与波.聂在平, 柳清伙译.北京:电子工业出版社, 1995 Chew W C. Waves and Fields in Inhomogeneous Media (in Chinese). Translated by Nie Z P, Liu Q H. Beijing:Electronic Industry Press, 1995 |
| [31] | Patterson T N L. The optimum addition of points to quadrature formulae. Mathematics of Computation , 1968, 22(104): 847-856. DOI:10.1090/S0025-5718-68-99866-9 |
| [32] | Chave A D. Numerical integration of related Hankel transforms by quadrature and continued fraction expansion. Geophysics , 1983, 48(12): 1671-1686. DOI:10.1190/1.1441448 |
| [33] | 张弛平, 施云慧. 计算方法. 北京: 科学出版社, 2003 . Zhang C P, Shi Y H. Calculation Method (in Chinese). Beijing: Science Press, 2003 . |
| [34] | Bunse G A, Byers R, Mehrmann V. A chart of numerical methods for structured eigenvaluse problems. SIAM Journal of Matrix Analysis and Its Applications , 1992, 13: 419-453. DOI:10.1137/0613028 |
 2010, Vol. 53
2010, Vol. 53