地球物理学报  2010, Vol. 53 Issue (12): 2955-2963   PDF    
引用本文
毛剑, 吴如山, 高静怀 等. 局部指数标架小波束在复杂介质方向照明分析中的应用. 地球物理学报, 2010, 53(12): 2955-2963, doi: 10.3969/j.issn.0001-5733.2010.12.019.  
Mao J, Wu R S, Gao J H, et al. Directional illumination analysis for complex medium using local exponential frame beamlet. Chinese J. Geophys. (in Chinese), 2010, 53(12): 2955-2963, doi: 10.3969/j.issn.0001-5733.2010.12.019.  
局部指数标架小波束在复杂介质方向照明分析中的应用
毛剑1,2 , 吴如山2 , 高静怀1 , 耿瑜1,2     
1. 西安交通大学电子与信息工程学院波动与信息研究所, 西安 710049;
2. Modeling and Imaging Laboratory, University of California, Santa Cruz 95064, U. S. A
收稿日期 2009-12-15, 2010-12-02 收修定稿
基金项目: 国家自然科学基金重点项目(40730424), 国家自然科学基金面上项目(40674064)和国家"863"高技术项目(2006AA09A102)资助
作者简介: 毛剑, 男, 1980年生, 在读博士研究生, 就读于西安交通大学.主要从事复杂介质中地震波传播与成像及地震资料处理的理论与方法等研究.E-mailarrowspirit@gmail.com
通讯作者: 高静怀, 男, 1960年生, 教授, 博士生导师.主要从事地震波传播、成像、地震资料处理以及信号处理等方面的研究
摘要: 提出了用局部指数标架小波束进行角度域分解的方法, 解决了局部余弦基和局部正弦基缺乏单一方向性的问题.局部指数标架由局部余弦基和局部正弦基线性组合而成, 是冗余度为2的紧标架.利用局部余弦变换和局部正弦变换的快速算法, 能使基于局部指数标架进行方向照明分析的计算效率较常用的局部倾斜叠加和Gabor-Daubechies标架等方法具有更为明显的优势.通过计算二维SEG/EAGE模型和SIGSBEE模型的方向照明图以及采集系统倾角响应图证实了本文方法的有效性.该方法的高效性使其在三维模型的方向照明分析和大规模的工业应用中具有广阔前景.
关键词: 局部余弦基      局部指数标架      局部角度域      偏移成像      方向照明分析      采集孔径     
Directional illumination analysis for complex medium using local exponential frame beamlet
MAO Jian1,2, WU Ru-Shan2, GAO Jing-Huai1, GENG Yu1,2     
1. Institute of Wave and Information, School of Electronic and Information Engineering, Xi'an Jiaotong University, Xi'an 710049, China;
2. Modeling and Imaging Laboratory, University of California, Santa Cruz 95064, U. S. A
Abstract: We develop an efficient wavefield decomposition method in the local-angle-domain using local exponential frame (LEF) beamlets, which overcomes the lack of uniquely defined directional localization of local cosine bases (LCB) and local sine bases (LSB). The wavefield is decomposed in the local angle domain by using the local exponential beamlet, which is a tight frame with redundancy ratio 2 and implemented by a linear combination of local cosine and sine transforms. As the local cosine/sine transforms have fast algorithms, this method has much better efficiency than the decomposition methods previously used in directional illumination analysis, such as the local slant stacking or Gabor-Daubechies frame method. The directional illumination (DI) maps and the acquisition dip responses (ADR) for the 2D SEG/EAGE salt model and SIGSBEE model demonstrate the validity and feasibility of our method. Furthermore, because of its high computational efficiency, the new method makes the 3D directional illumination analysis readily applicable in the industry..
Key words: Local cosine basis      Local exponential frame      Local angle domain      Migration imaging      Directional illumination analysis      Acquisition aperture     
1 引言

照明分析为研究采集孔径和采集系统几何对目标区域偏移成像质量的影响提供了一个强有力的工具.许多先前的照明强度分析方法都是基于射线追踪的方法[1~4].虽然射线方法方便高效并且可以提供具有方向性的照明分析, 但同时也存在一些限制(比如在某些复杂区域会产生较大误差).因此我们需要发展基于波动方程理论的照明方法.

单程波算子已经在照明分析中得到了广泛的应用, 可以解决多路径效应, 包括聚焦、散焦以及衍射等问题.与射线方法有所不同, 基于单程波的传播算子在传播过程中不能提供跟角度有关的方向信息.随着小波束(beamlet)理论的发展[5~10], 频率域波场的局部角度信息可以通过小波束分解或者局部倾斜叠加(localslantstack)[11]得到, 并成功地用于方向照明分析[10, 12].Gabor-Daubechies标架[5~7, 9]分解完备但非正交, 因此具有冗余性.由于Gabor-Daubechies标架在冗余度小于4时需要计算对偶标架, 并且不够稳定, 所以在实际应用中需要选择冗余度大于等于4的标架, 从而不能达到较高的计算效率.而通过局部倾斜叠加方法进行波场分解的计算效率则更低.局部余弦基[9, 13~15]正交并具有快速算法, 但局部余弦小波束通常有两个对称的波瓣, 缺乏单一定义的方向性, 使其不能用于方向照明分析.

本文提出用具有单一方向定义的局部指数紧标架进行波场分解以获得角度信息.局部指数标架由局部余弦基和局部正弦基线性组合而成, 是冗余度为2的紧标架.由于局部余弦变换和局部正弦变换具有快速算法, 该方法提供了一种高效的获得局部角度信息的方法.本文主要讨论方向照明分析技术在单程波算子下的应用, 该方法也可发展为适用于全波方程的算法.另外本文主要以二维模型为例证明了其有效性, 该方法在三维模型的方向照明分析中的应用将在后续文章中详细讨论.本文第2节主要介绍局部指数标架理论及其在波场分解中的应用; 第3节讨论了在角度域进行方向照明分析的一些基本定义和基本理论; 第4节通过二维SEG/EAGE盐丘模型的方向照明分析说明了该方法的有效性, 同时与局部倾斜叠加方法进行了对比, 然后用该方法对更为复杂的二维SIGSBEE模型进行了方向照明的计算.最后进行了计算效率分析.

2 局部指数标架及其在波场分解中的应用 2.1 局部余弦/正弦基

空间-频率域波场可以通过小波束进行分解, 从而得到空间和方向都具有局部化性质的波场.正交基(如局部正弦基)和紧标架(如Gabor-Daubechies标架)都可用于小波束分解.考虑到计算效率, 我们更倾向于用没有冗余度并且具有快速算法的正交基.Balian-Low定理[16]证明高斯窗调制的指数函数不能构成有很好频率局部化特性的基.然而Coifman和Meyer[13]成功地利用光滑交叠的钟形函数(bell function)调制余弦/正弦函数构造了局部余弦/正弦基[14, 15].

局部余弦/正弦基函数的定义如下

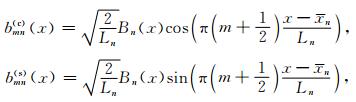
(1)

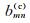
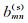
(x)和 (x)分别代表局部余弦基(如图 1所示)和局部正弦基.其中xn为区间起始位置, Ln=xn+1-xn为区间长度, m为局部水平波数指标, 钟形窗函数Bn(x)是定义在紧支集[xn-ε, xn+1+ε′]上的光滑函数, 并且xn+ε≤xn+1-ε′, ε和ε′分别为区间左边、右边的重叠半径.

图 1 局部余弦基函数 Fig. 1 Local cosine basis

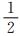
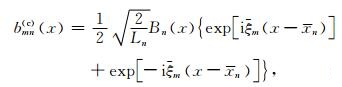
从公式(1)看出, 局部余弦基是由钟形窗调制的余弦函数, 因此非常适用于波场分解.并且由于其正交性, 波场用局部余弦基分解的系数矩阵具有很好的稀疏性.局部余弦基算子也已经被证明是一种精确高效的单程波传播算子[9].但局部正弦/余弦基不具有单一方向性, 即在波数域有两个对称的波瓣.令ξm=π(m+)/Ln为局部水平波数, 局部余弦基函数可表示为

(2)

公式(2)中的两个指数项表明局部余弦基小波束有两个对称的波瓣, 即沿关于z轴对称的两个方向传播. 图 3给出了单个局部余弦小波束在二维S EG / EAGE盐丘模型(图 2所示)中传播的情况.正是因为缺乏单一的方向性, 局部余弦基和局部正弦基都不能直接用于方向照明分析.

图 2 二维SEG/EAGE盐丘模型 Fig. 2 2D SEG/EAGE salt model
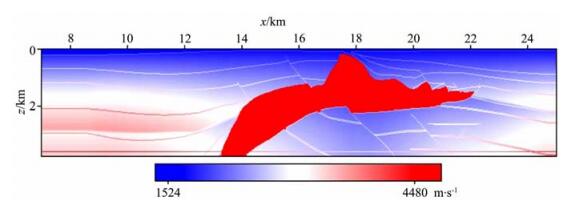
图 3 单个局部余弦小波束(15 Hz)在二维SEG/EAGE盐丘模型中的传播 Fig. 3 A single local cosine beamlet (15 Hz) propagation in the 2D SEG/EAGE salt model

事实上, 这些基函数都是由局部指数紧标架线性组合而来的[17, 18].本文中, 我们仍使用正交基进行波场的分解与传播, 然后再通过一次额外的正交变换得到局部指数标架分解系数, 从而得到局部角度域信息.如果使用局部余弦基进行波场分解和延拓, 则只需一次额外的局部正弦分解就可得到局部指数标架的分解系数.这样使得波场传播及角度信息的获得都具有很高的效率.

2.2 局部指数标架

为了提高传播精度同时引入方向性以便在角度域进行操作, 我们提出了局部谐和基(local harmonic bases)[19]和局部指数标架的波场分解方法.前者为完备正交基, 适用于波场的分解和传播, 具有单一方向性定义; 后者为紧标架, 具有冗余度, 提供了全部的角度域信息(包含相位信息), 本文主要讨论局部指数标架在角度域的方向照明分析方面的应用.

局部指数标架定义为

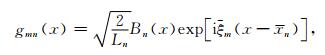
(3)

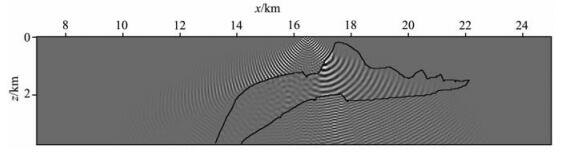
其中m=-M, …, -1, 0, …, M-1, n=0, …, N-1.M和N的定义与局部余弦/正弦基的定义相同.为了利用局部余弦/正弦变换的快速算法, 我们将局部指数函数分为两组

(4)

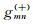
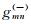
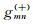
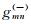
其中m=0, …, M-1.我们称(x)和(x)分别为右传播-和左传播-局部指数标架小波束.由于局部指数标架变换需要两次正交变换(一次局部余弦变换和一次局部正弦变换), (x)和(x)一同构成冗余度为2的局部指数标架.图 4给出了局部指数标架小波束在二维SEG/EAGE模型中的传播情况.局部指数标架具有单一方向性并且具备快速算法, 因此可以用于高效率的方向照明分析.

图 4 局部指数标架小波束（15 HZ)在二维SEG/EAGE模型中的传播 (a) 向左传的局部指数标架小波束；(b) 向右传的局部指数标架小波束. Fig. 4 Local exponential frame beamlet (15 Hz) propagation in 2D SEG/EAGE model (a) Lett propagating LEF beamlet; (b) Right propagating LEF beamlet.
2.3 利用局部指数标架进行波场分解

空间-频率域的标量波波动方程定义如下

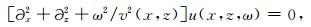
(5)

其中ω为频率, v(x, z)为速度, u(x, z, ω)为空间-频率域波场.

深度z处的空间-频率域波场可沿x轴用局部指数标架小波束分解如下

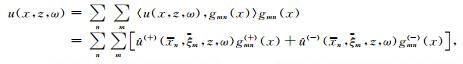
(6)

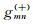
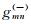
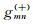
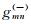
其中 (x)和 (x)为前面提到的局部指数标架小波束, û(+) (xn, ξm, z, ω)和û(-) (xn, ξm, z, ω)分别为关于 (x)和 (x)的小波束分解系数, xn为窗口位置, 〈, 〉表示内积, 即〈u(x, z), gmn(x)〉=∫u(x, z)(gmn(x))*dx.

波场用局部指数标架分解的系数可计算如下

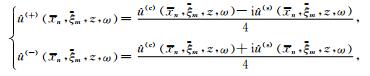
(7)

其中û(c) (xn, ξm, z, ω)和û(s) (xn, ξm, z, ω)分别为波场用局部余弦基和局部正弦基分解的复数系数.

经过局部指数标架分解后, 空间域的波场变换为在空间和波数域同时具有局部化性质的波场.局部指数标架的分解系数只提供了每一个窗口的角度信息, 而每个空间点的角度信息需要从这些分解系数中提取, 我们称这个过程为部分重构.

将公式(6)写为如下形式

(8)

得到局部波数域波场的部分重构式(局部相空间混和域波场)

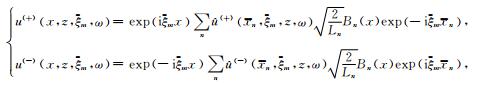
(9)

我们称u(+)(x, z, ξm, ω)或u(-)(x, z, ξm, ω)为局部平面波, 即相邻两个窗口相同局部波数的平面波加权平均的结果.

对于局部水平波数为ξm的局部平面波, 相应的局部传播角度可换算如下

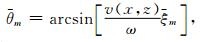
(10)

其中θm为相对于垂向的入射角.由公式(10)即可在局部角度域和局部波数域之间进行转换.

3 方向照明分析理论[10, 12]

对于给定的采集系统, 从源s出发到地下一点(x, z)的频率-空间域格林函数可以在成像区域分解为不同的局部波数平面波分量

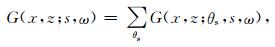
(11)

其中G(x, z; s, ω)为频率-空间域格林函数, G(x, z; θs, s, ω)为关于入射角θs的局部角度分量.类似地, 从接收器g出发到(x, z)的频率-空间域格林函数可以分解如下

(12)

其中G(x, z; g, ω)为频率-空间域格林函数, G(x, z; θg, g, ω)为关于接收角θg的局部角度分量.

为了估计给定速度模型和采集系统在局部角度域的照明能量分布, 我们对每个局部入射角将所有的源到成像点的贡献都叠加起来, 即

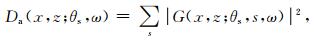
(13)

其中D a(x, z; θs, ω)即为方向照明强度DI (directional illumination).

将所有角度的方向照明能量都叠加在一起即得到照明总强度

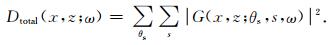
(14)

针对地下任何一个散射点, 所有有效的发射/接收组合对该点的能量贡献, 是对采集系统的有效评价.为了描述采集系统的探测孔径及传播效应对给定一对发射/接收角组合的能量分布, 我们对整个采集系统的源和接收器都用单位脉冲进行衡量.与计算照明强度类似, 将所有对应于每个发射/接收角组合的格林函数的贡献相加即可得到采集系统效验矩阵AAE (acquisition aperture efficacy), 这里我们忽略波传播的相位信息而只考虑对于采集系统的能量分布. (x, z)处的采集系统效验矩阵定义如下

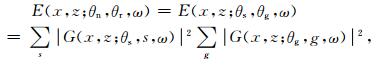
(15)

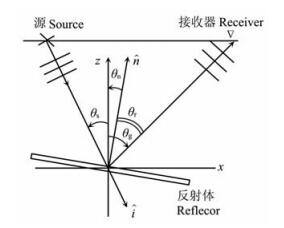
其中θn为反射面关于垂向的夹角, θr为反射角(见图 5)[10].(θn, θr)和(θs, θg)的关系为

图 5 反射体倾角和反射角的定义示意图 Fig. 5 A sketch of dip angle and reflection angle

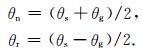
(16)

进一步将采集系统效验矩阵化简可以得到相对不同反射体倾角的能量分布

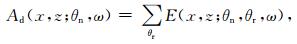
(17)

其中Ad(x, z; θn, ω)为采集系统倾角响应ADR (acquisition dip response), 用于衡量采集系统关于源和接收器分布对于给定倾角反射体的照明强弱.

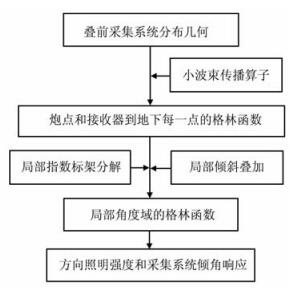
4 方向照明分析流程及模型算例分析 4.1 方向照明分析流程

结合第2节和第3节中的内容, 对给定模型进行方向照明分析流程(图 6给出了流程图)可总结如下:

图 6 方向照明分析流程图 Fig. 6 Workflow of directional Ulumination analysis

(1) 由采集系统分布几何确定需要计算的格林函数;

(2) 用小波束传播算子计算每个炮点和每个接收器点到地下每一点的格林函数;

(3) 将格林函数分解到局部角度域(原有的方法是采用局部倾斜叠加方法分解, 本文采用第2节所给出的局部指数标架分解, 并与之比较);

(4) 基于第3节中的照明分析公式计算方向照明强度和采集系统倾角响应图.

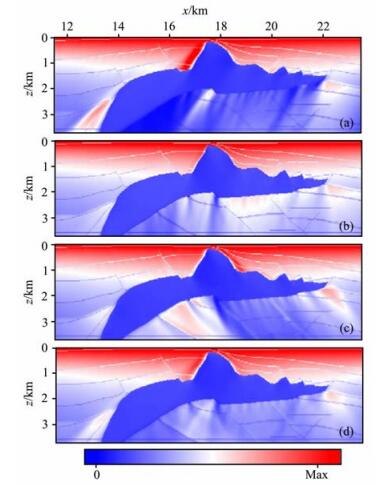
4.2 二维SEG/EAGE盐丘模型

我们首先用局部指数标架方法对二维SEG/EAGE盐丘模型进行了方向照明分析, 同时与局部倾斜叠加方法进行了比较.二维SEG/EAGE模型在水平方向有1200个采样点, 采样间隔为25 m, 在深度方向有150个采样点, 采样间隔同为25 m.最小的速度为1524 m/s, 最大速度为4480 m/s, 速度模型如图 2所示.叠前数据共325炮, 每炮源的位置间隔50 m, 每炮的接收器为176个, 间隔25 m, 并且为左边单边接收.图 7和图 8分别为利用局部倾斜叠加方法和局部指数标架方法计算得到的方向照明分析图.通过比较可以看出, 采用局部指数标架小波束的方法在照明分析质量上与计算效率较低的局部倾斜叠加方法基本相同.图 9为利用局部指数标架计算得到的采集系统倾角响应图.从这些方向照明图和倾角响应图可以看出盐丘下方的区域对于不同入射角和不同倾角的照明能量分布, 说明了偏移成像的振幅是与角度有关的.阴影区表明了照明能量较弱的区域, 也就是成像质量可能较差的区域.

图 7 对二维SEG/EAGE模型利用局部倾斜叠加方法计算出的方向照明图 (a) 入射角θs=-30°的方向照明强度; (b) 入射角θs=0°的方向照明强度；(c) 入射角θs=30°的方向照明强度；(d) 照明总强度 Fig. 7 Directional illumination (DI) maps for 2D SEG/EAGE model using the local slant stack method (a) DI map for incident angle θs=-30°; (b) DI map for incident angle θs=0°; (c) DI for incident angle θs=30°; (d) Total illumination.
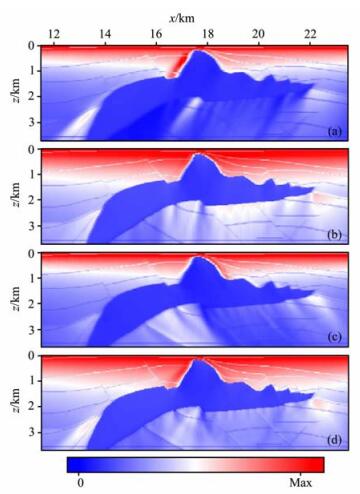
图 8 同图 7, 但为利用局部指数标架方法计算出的方向照明图 Fig. 8 Same as Fig.7, but for directional illumination (DI) maps using the local exponential framede composition
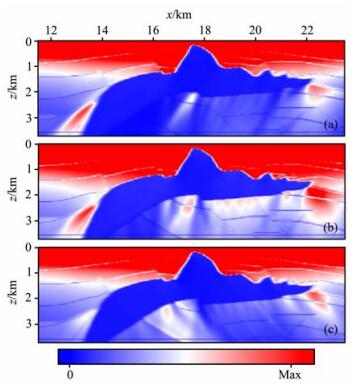
图 9 对二维SEG/EAGE模型利用局部指数标架方法计算出的采集系统倾角响应图 (a) 倾角θn=-20°的采集系统倾角响应; (b)倾角θn=0°的采集系统倾角响应; (c) 倾角θn=20°的采集系统倾角响应. Fig. 9 Acquisition dip response (ADR) for 2D SEG/ EAGE model using the local exponential frame decomposition (a) ADR map for dip angle θn=-20°; (b) ADR map for dip angle θn=0°; (c) ADR map for dip angle θn=20°
4.3 SIGSBEE模型

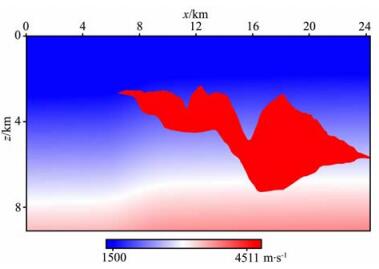
进一步用局部指数标架小波束方法计算了更复杂的二维SIGSBEE模型方向照明分析图.SIGSBEE模型在水平方向有2133个采样点, 采样间隔为11.4 m, 在深度方向有1200个采样点, 采样间隔为7.6 m.最小的速度为1500 m/s, 最大速度为4511 m/s, 速度模型如图 10所示.叠前数据共500炮, 每炮源的位置间隔45 m, 每炮的接收器为348个, 间隔22.5 m, 并且为左边单边接收.图 11为利用局部指数标架方法计算得到的方向照明分析图.

图 10 二维SIGSBEE盐丘模型 Fig. 10 2D SIGSBEE satt model
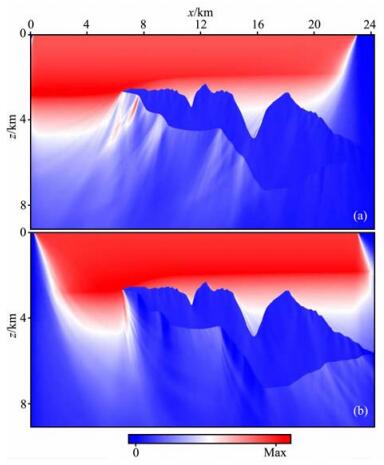
图 11 对二维SIGSBEE模型利用局部指数标架方法计算出的方向照明图 (a) 人射角θs=-30°的方向照明强度；(b) 人射角θs=30°的方向照明强度. Fig. 11 Directional illumination (DI) maps for 2D SIGSBEE model using the local exponential frame decomposition (a) DImap for incident angle θs=-30°; (b) DImap for incident angle θs=30°.
4.4 效率分析

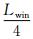
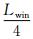
为了进一步验证本文方法的有效性, 将同已有的局部倾斜叠加和Gabor-Daubechies标架方法进行计算效率方面的对比.假设局部倾斜叠加(或者Gabor-Daubechies标架)中的高斯窗和局部指数标架中的钟形窗具有同样的宽度Lwin.则对于局部倾斜叠加方法, 每一个点需要O(LwinLwin)阶的运算, 所以共需要O(NLwinLwin)阶的运算(N为总采样点数).对Gabor-Daubechies标架分解, 每个高斯窗口都需要一个O(Lwinlog2Lwin)阶的FFT运算.为了保证Gabor-Daubechies标架分解的稳定性, 一般需要选择冗余度大于等于4的标架, 因此总共需要O(4Nlog2Lwin)阶的运算(如果冗余度等于4).而对于局部指数标架分解我们则只需要一次局部余弦变换和一次局部正弦变换, 每个局部窗口内的运算阶数为OLwinlog2(由于在快速局部余弦/正弦变换中使用了折叠技术), 进而总的运算阶数为O2Nlog2.比如窗口长度为Lwin=16, 则局部倾斜叠加、Gabor-Daubechies标架方法和局部指数标架方法所需的运算阶数分别为O(256N), O(16N)和O(4N).另一方面, 若使用局部余弦基的传播算子, 则局部余弦基的分解系数在传播时已经得到, 因而只需要在此基础上再进行一次局部正弦基分解就可得到局部指数标架分解系数.总而言之, 局部指数标架方法比Gabor-Daubechies标架方法和局部倾斜叠加方法在效率上有较大幅度的提高.表 1给出了在单个节点单CPU (主频为3GHz)情况下对于不同模型照明分析计算所需的CPU时间的对比.可见, 局部指数标架方法在复杂模型的照明分析计算中的效率优势更为突出, 更适合工业界大规模的应用.

表 1 利用局部指数标架方法和局部倾斜叠加方法CPU计算时间对比 Table 1 Comparison of CPU computational time for the local exponential method and local slant stacking method
5 结论与讨论

本文发展了一种利用局部指数标架小波束进行角度域方向照明分析的有效方法.这种局部指数标架的冗余度为2, 因此不是正交基.然而, 由于局部余弦基的分解系数在传播时已经得到, 所以只需要一次额外的局部正弦基分解就可得到局部指数分解系数.并且局部正弦/余弦变换的快速算法使得这种方法相对于局部倾斜叠加和Gabor-Daubechies标架方法具有更高的效率.从二维SEG/EAGE盐丘模型和二维SIGSBEE模型的方向照明分析和采集系统倾角响应图可以看出这种方法的有效性和适用性.我们将在以后讨论如何将该方法推广到三维方向照明分析应用中.另外, 本文方法可以发展为在角度域进行振幅校正的高效真反射成像方法.

致谢

感谢谢小碧、曹军、郑应才、陈文超在这项工作上的宝贵意见, 感谢杨辉、何耀峰在程序编写上的帮助.

参考文献
[1] Bear G, Liu C, Lu R, Willen D, et al. The construction of subsurface illumination and amplitude maps via ray tracing. The Leading Edge , 2000, 19(7): 726-728. DOI:10.1190/1.1438700
[2] Muerdter D, Ratcliff D. Understanding subsalt illumination through ray-trace modeling, Part 1:Simple 2D salt models. The Leading Edge , 2001, 20(6): 578-594. DOI:10.1190/1.1438998
[3] Muerdter D, Kelly M, Ratcliff D. Understanding subsalt illumination through ray-trace modeling, Part 2:Dipping salt bodies, salt peaks, and nonreciprocity of subsalt amplitude response. The Leading Edge , 2001, 20(7): 688-687. DOI:10.1190/1.1487279
[4] Muerdter D, Ratcliff D. Understanding subsalt illumination through ray-trace modeling, Part 3:Salt ridges and furrows, and impact of acquisition orientation. The Leading Edge , 2001, 20(8): 803-816. DOI:10.1190/1.1487289
[5] Wu R S, Wang Y Z, Gao J H. Beamlet migration based on local perturbation theory. 70th Annual Meeting, SEG, Expanded Abstracts, 2000.1008~1011
[6] Chen L, Wu R S, Chen Y. Target-oriented beamlet migration based on Gabor-Daubechies frame decomposition. Geophysics , 2006, 71(2): S37-S52. DOI:10.1190/1.2187781
[7] 陈凌, 吴如山, 王伟君. 基于Gabor-Daubechies小波束叠前深度偏移的角度域共成像道集. 地球物理学报 , 2004, 47(5): 876–885. Chen L, Wu R S, Wang W J. Common angle image gathers obtained from Gabor-Daubechies beamlet prestack depth migration. Chinese J. Geophys. (in Chinese) , 2004, 47(5): 876-885.
[8] 陈凌, 吴如山, 陈颙. 基于Gabor-Daubechies小波束域波场外推的散射系数矩阵的计算及其应用. 地球物理学报 , 2004, 47(2): 289–298. Chen L, Wu R S, Chen Y. Construction and application of local scattering matrix based on wavefield extrapolation in the Gabor-Daubechies beamlet domain. Chinese J. Geophys. (in Chinese) , 2004, 47(2): 289-298.
[9] Wu R S, Wang Y Z, Luo M Q. Beamlet migration using local cosine basis. Geophysics , 2008, 73(5): S207-S217. DOI:10.1190/1.2969776
[10] Wu R S, Chen L. Directional illumination analysis using beamlet decomposition and propagation. Geophysics , 2006, 71(4): S147-S159. DOI:10.1190/1.2204963
[11] Xie X B, Wu R S. Extracting angle domain information from migrated wavefield. 72nd Annual International Meeting, SEG, Expanded Abstracts, 2002.1360~1363
[12] Xie X B, Jin S W, Wu R S. Wave-equation-based seismic illumination analysis. Geophysics , 2006, 71(5): S169-S177. DOI:10.1190/1.2227619
[13] Coifman R R, Meyer Y. Remarques sur l'analyse de Fourier a fenetre. Comptes Rendus de l'Academie des Sciences:Paris, Serie I , 1991, 312: 259-261.
[14] Mallat S. A Wavelet Tour of Signal Processing, Second Edition. Academic Press, 1999
[15] Wickerhauser M V. Adapted Wavelet Analysis from Theory to Software. A K Peters, 1994
[16] Balian R. Un principle d'incertitude en theorie du signal ou en mecanique quantique. Comptes Rendus de l'Academie des Sciences, Paris, Serie Ⅱ , 1981, 292: 1357-1362.
[17] Daubechies I, Jaffard S, Journé J L. A simple Wison orthonormal basis with exponential decay. SIAM J. Math. Anal. , 1991, 22(2): 554-573. DOI:10.1137/0522035
[18] Auscher P. Remarks on the local Fourier bases. In:Benedetto J J, Frazier M W eds. Wavelets, Mathematica and Applications. CRC Press, 1994. 203~218
[19] 毛剑, 吴如山, 高静怀. 利用局部谐和基小波束的高精度叠前深度域偏移成像方法研究. 地球物理学报 , 2010, 53(10): 2442–2451. Mao J, Wu R S, Gao J H. High-accuracy prestack depth migration and imaging using local harmonic basis beamlet. Chinese J. Geophys. (in Chinese) , 2010, 53(10): 2442-2451.